Coordenadas cilíndricas parabólicas
Este artigo ou secção contém uma lista de referências no fim do texto, mas as suas fontes não são claras porque não são citadas no corpo do artigo, o que compromete a confiabilidade das informações. (Maio de 2012) |
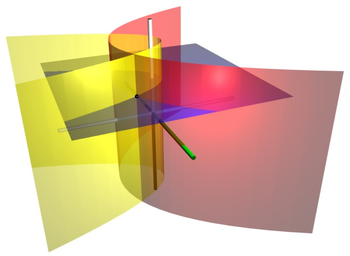
Em matemática, as coordenadas cilíndricas parabólicas são um sistema de coordenadas ortogonais tridimensionais que resultam da projeção do sistema de coordenadas parabólicas bidimensional na direção perpendicular a . Assim, as superfícies coordenadas são cilindros parabólicos confocais. As coordenadas cilíndricas parabólicas possuem inúmeras aplicações como, por exemplo, na teoria potencial das arestas.
Definição básica[editar | editar código-fonte]
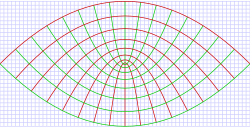
As coordenadas cilíndricas parabólicas são definidas em termos das coordenadas cartesianas (x,y,z) por:
As superfícies com constante formam cilindros parabólicos confocais de equações
com concavidade voltada para a direção , ao passo que as superfícies com constante formam cilindros parabólicos confocais de equações
com concavidade voltada para a direção oposta, isto é, na direção . Os focos de todos estes cilindros parabólicos estão localizados ao longo da reta definida por . O raio r tem uma equação simples, a saber,
que é útil na resolução da equação de Hamilton-Jacobi em coordenadas parabólicas para o problema da forca central inversa ao quadrado da distância, da mecânica. Para mais detalhes, ver o artigo vetor de Laplace-Runge-Lenz.
Fatores de escala[editar | editar código-fonte]
Os fatores de escala para as coordenadas cilíndricas parabólicas e são:
O elemento infinitesimal de volume é
e o laplaciano é igual a
Outros operadores diferenciais tais como e podem ser expressos nas coordenadas substituindo-se os fatores de escala nas fórmulas gerais em coordenadas ortogonais.
Harmônicos cilindro parabólico[editar | editar código-fonte]
Uma vez que todas as superfícies com σ, τ and z são conicóides, a equação de Laplace é separável em coordenadas cilíndricas parabólicas. Usando a técnica da separação de variáveis, uma solução independente para a equação de Laplace pode ser escrita como:
E a equaçao de Laplace, ao ser dividida por V , é escrita como:
Uma vez que a equação em Z está separada dos outros termos, podemos escrever
Onde m é constante. A solução para Z(z) é:
Substituindo por , a equação de Laplace agora pode ser escrita como:
Ainda podemos separar as funções S e T e introduzir uma constante para obter:
As soluções para essas equaçoes são as funções cilindro parabólico
Os harmônicos cilindro parabólico para (m,n) são então o produto das soluções. A combinação reduz o número de constantes e a solução geral para a equação de Laplace pode ser escrita como:
Aplicações[editar | editar código-fonte]
As aplicações clássicas das coordenadas cilíndricas parabólicas encontram-se na resolução de equações diferenciais parciais, como por exemplo a equação de Laplace ou a equação de Helmholtz, para as quais essas coordenadas permitem a utilização da técnica de separação das variáveis. Um exemplo típico seria o [[campo eletrico em torno de uma placa plana semi-infinita condutora.
Ver também[editar | editar código-fonte]
- Coordenadas ortogonais
- Sistemas de coordenadas ortogonais bidimensionais:
- Sistemas de coordenadas ortogonais tridimensionais:
- Sistema de coordenadas cartesianas
- Sistema de coordenadas cilíndricas
- Sistema de coordenadas esféricas
- Sistema de coordenadas parabólicas
- Coordenadas cilíndricas parabólicas
- Coordenadas paraboloidais
- Coordenadas esferoidais oblatas
- Coordenadas esferoidais prolatas
- Coordenadas elipsoidais
- Coordenadas cilíndricas elípticas
- Coordenadas toroidais
- Coordenadas biesféricas
- Coordenadas cilíndricas bipolares
- Coordenadas cônicas
- Coordenadas cíclides anel-plano
- Coordenadas cíclides disco plano
- Coordenadas bicíclides
- Coordenadas cap-cíclides
Referências[editar | editar código-fonte]
- Este artigo foi inicialmente traduzido, total ou parcialmente, do artigo da Wikipédia em inglês cujo título é «Parabolic cylindrical coordinates», especificamente desta versão.
- Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 658. ISBN [[Special:BookSources/0-07-043316-X, |0-07-043316-X, <span class="noprint">[[Library of Congress Control Number|LCCN]] [http://lccn.loc.gov/52011515 52-11515]</span>]] Verifique
|isbn=(ajuda) - Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 186–187.
- Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 181. , ASIN B0000CKZX7
- Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. p. 96.
- Zwillinger D (1992). Handbook of Integration. Boston, MA: Jones and Bartlett. p. 114. ISBN 0-86720-293-9 Same as Morse & Feshbach (1953), substituting uk for ξk.
- Moon P, Spencer DE (1988). «Parabolic-Cylinder Coordinates (μ, ν, z)». Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd, 3rd print ed. New York: Springer-Verlag. pp. 21–24 (Table 1.04). ISBN 978-0387184302






















![{\displaystyle {\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {\ddot {S}}{S}}+{\frac {\ddot {T}}{T}}\right]+{\frac {\ddot {Z}}{Z}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99190e6afe07d230b871dd5a2f159b9cf8179d2c)




![{\displaystyle \left[{\frac {\ddot {S}}{S}}+{\frac {\ddot {T}}{T}}\right]=m^{2}(\sigma ^{2}+\tau ^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/544c991ae2342d2a4f196e566d4357f7195a7c6c)





