Superelipse

A superelipse[1] (também chamada de curva de Lamé, em homenagem a Gabriel Lamé, matemático francês que a estudou) é uma figura geométrica definida no sistema de coordenadas cartesiano como o conjunto de todos os pontos (x, y) tais que
Essa fórmula define uma curva contida no retângulo −a ≤ x ≤ +a e −b ≤ y ≤ +b. Aos parâmetros a e b se dá o nome de semi-diâmetros da curva.
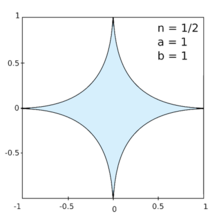
Quando a superelipse se parece com uma estrela de quatro pontas com lados côncavos. Para n = 1/2, particularmente, cada um dos quatro arcos é uma curva de Bézier quadrática definida pelos dois eixos; como resultado, cada arco é um segmento de parábola.
Quando a curva é um losango com cantos (±a, 0) e (0, ±b). Quando ela parece um losango com esses mesmos cantos mas com lados convexos.
Quando a curva é uma elipse ordinária (ou um círculo, se a = b). Quando a curva se parece com um retângulo de cantos arredondados. A curvatura é nula nos pontos (±a, 0) e (0, ±b).
Se a curva é também chamada hipoelipse. Quanto mais baixo o valor de n (ou seja, quando n tende a −∞), mais a figura assemelha-se a uma cruz.
Se a forma pode ser chamada hiperelipse. Quanto mais alto é o valor que se atribui a n (isto é, quando n tende a +∞), mais a imagem se parece com um retângulo
Os efeitos de n[editar | editar código-fonte]


Quando n é um número racional com um numerador par e um numerador ímpar, então a superelipse é uma curva algébrica plana. Em particular, quando a e b são ambos iguais a 1 e n é um inteiro par, temos uma curva de Fermat da grau n. Neste caso ela é não-singular, mas em geral ela será singular. Se o numerador não for par, então a curva e composta de porções de mesma curva algébrica em diferentes orientações.
Por exemplo, se x4/3 + y4/3=1, então a curve é uma curva algébrica de grau doze e gênero três, dada pela equação
Generalização[editar | editar código-fonte]

A superelipse é posteriormente generalizada através da fórmula:
História[editar | editar código-fonte]
Apesar de ser comummente creditado como seu inventor, o poeta e cientista dinamarquês Piet Hein (1905-1996) não descobriu a superelipse. A notação cartesiana geral da forma vem do matemático francês Gabriel Lamé (1795-1870) que generalizou a equação para a elipse.

Entretanto, Piet Hein popularizou o uso da superelipse em arquitetura, planejamento urbano, e projeto de móveis, sendo ele o inventor do "super ovo" ou "super elipsoide" partindo da superelipse
Os urbanistas em Estocolmo, Suécia necessitavam de uma solução para uma modernização nas antigas cidade de Sergels Torg. A superelipse de Piet Hein proveu a solução prática e estética. Em 1969, negociadores em Paris da Guerra do Vietnã não concordaram com o formato da mesa de negociação. Piet Hein projetou uma mesa superelíptica especial que acomodou a todos. A superelipse foi utilizada com o formato do Estádio Azteca, na Cidade do México.
Hermann Zapf e Donald Knuth fizeram uso extensivo da superelipses em tipografia, Zapf por razões estéticas e Knuth parcialmente por razões técnicas. Como as curvas de Bezier, as superelipser são mais fáceis de implementar com a aritmética inteira do que são os arcos circulares, então Knuth utilizou superelipses ao invés de arcos circulares em seu software de projeto de tipo Metafonte. Entretanto, Zapf devia ter aprendido sobre superelipses muito antes de sua famosa colaboração com Knuth, visto que a fonte Melior de Zapf construída em 1950 possui curvas superelípticas e Knuth veio a se interessar em tipografia posteriormente depois. Muitas fontes afirmam que Zapf desenhava os formatos da Melior à mão sem conhecer o conceito matemático da superelipse, e somente posteriormente Piet Hein mostrou a Zapf que as curvas que ele utilizavam eram extremamente similares à construção matemática da superelipse, porém tal dado não é confirmado.
Ver também[editar | editar código-fonte]
- Elipse
- Elipsoide, a uma analogia de uma elipse em uma dimensão superior
- Esferoide, o elipsoide obtido através da rotação de uma elipse ao redor de seu eixo maior ou menor
- Astroide, um elipsoide particular (n = 2/3, a = b = 1)
- Superquádricas
Referências
- ↑ Ciberdúvidas/ISCTE-IUL. «Glossário - Ciberdúvidas da Língua Portuguesa». ciberduvidas.iscte-iul.pt. Consultado em 13 de abril de 2018
Ligações externas[editar | editar código-fonte]
- «Superellipse (MathWorld)»
- «Lamé's Super Ellipse (Java-Applet)»
- «Super Ellipsoid (Java-Applet)»
- «Johan Gielis'». and Bert Beirinckx' "Superformula".
- Gardner, Martin: Piet Hein's Superellipse. - in Gardner, Martin: Mathematical Carnival. A New Round-Up of Tantalizers and Puzzles from Scientific American. New York: Vintage, 1977, pp. 240–254.
- Johan Gielis: Inventing the circle. The geometry of nature. - Antwerpen : Geniaal Press, 2003. - ISBN 9080775614














