Cilindro

 Nota: Para outros significados, veja Cilindro (desambiguação).

Um cilindro.

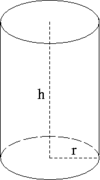
Em Geometria, um cilindro é o objeto tridimensional delimitado pela superfície de translação completa de um segmento de reta que se move paralelamente a si mesmo, e se apoia em uma circunferência. De maneira mais prática, o cilindro é um corpo alongado e de aparência redonda, com o mesmo diâmetro ao longo de todo o comprimento. Ao considerar-se um prisma de base regular, e fazer o número de lados/vértices da base tender ao infinito, o prisma tenderá a um cilindro.

Elementos

Os elementos do cilindro são

• Duas bases: são dois círculos congruentes e paralelos.
• Geratrizes: segmentos congruentes e paralelos entre os pontos da circunferência de uma base e os pontos correspondentes na outra base.
• Altura: distância entre os planos das bases.

Classificação

Os cilindros podem ser divididos em duas categorias, referentes ao ângulo entre a sua altura e o plano da base:

• Reto: se as geratrizes são perpendiculares aos planos das bases;
• Oblíquo: se as geratrizes são oblíquas (não-perpendiculares) aos planos das bases.

E, referente à relação entre a altura e o raio da base, apenas uma categoria relevante de classificação:

• Equilátero: é todo cilindro reto em que a altura é igual ao diâmetro da base, ou seja$$g=h=2r$$Assim, a secção meridiana é um quadrado.

Área e volume

Cilindro reto

Para um cilindro reto de raio $r$ e altura $h$,

• O volume é: $V=\pi r^{2}h$

• A área da base circular é igual à área de um círculo, $A_{B}=\pi r^{2}$, e a área lateral é $A_{L}=2\pi rh$

• A área total de sua superfície é $A_{T}=2A_{B}+A_{L}$, ou seja: $A_{T}=2\pi r(h+r)$

Otimização

Área mínima

Dado um volume fixo, pode-se descobrir qual a razão entre a altura e o raio de um cilindro reto para que a área seja mínima. Calcular a área mínima é útil em problemas de otimização de custo de produção, que deve ser diretamente proporcional à área.

Seja um cilindro reto de raio ${\textstyle r}$, altura ${\textstyle h}$ e volume fixo ${\textstyle V}$. A condição para que a área seja mínima é ${\textstyle h=2r}$.

Inicialmente, o volume é dado por:$$V=\pi r^{2}h$$Em seguida, a área em função de ${\textstyle r}$ e ${\textstyle V}$ é:
$$A=2\pi r^{2}+2\pi rh=2\pi r^{2}+{\frac {2V}{r}}$$Perceba que a função vai para o infinito positivo tanto quando o valor de ${\textstyle r}$ vai para ${\textstyle \infty }$ quanto para ${\textstyle 0}$. Logo, deve possuir um valor mínimo. O valor mínimo da função será um ponto crítico, quando a derivada for nula:
$${\begin{aligned}A(r)&=2\pi r^{2}+{\frac {2V}{r}}\\A'(r)&=4\pi r-{\frac {2V}{r^{2}}}\\A'(r)&=0\Leftrightarrow 4\pi r={\frac {2V}{r^{2}}}\Leftrightarrow V=2\pi r^{3}\end{aligned}}$$Igualando a equação volume-raio da área mínima com a equação inicial de volume:$$\pi r^{2}h=2\pi r^{3}$$Logo,$$h=2r$$Portanto, o cilindro reto de menor área dado um volume fixo é o cilindro equilátero, em que a altura é igual ao diâmetro da base. Tal otimização também é equivalente a maximizar o volume, dada uma área fixa.

Ver também

• Cone

Ligações externas

• Venturi, Jacir J. (2003). Cônicas e Quádricas (PDF) 5 ed. Curitiba: Unificado. 246 páginas. ISBN 8585132485