Triangulação de Delaunay

Em matemática, uma Triangulação de Delaunay para um conjunto de pontos P no plano é uma triangulação DT(P) onde nenhum ponto em P está dentro da circunferência formada por qualquer triângulo na DT(P). A Triangulação de Delaunay maximiza o menor ângulo de todos os triângulos na triangulação; esta tende a evitar triângulos com ângulos internos muito pequenos.

A triangulação foi inventada por Boris Delaunay em 1934.^[1] Para um conjunto de pontos em uma mesma linha, não existe Triangulação de Delaunay (o conceito de triangulação é desfeito para este caso). Para quatro ou mais pontos em um mesmo círculo (isto é, os pontos são cocirculares) a Triangulação de Delaunay não é única: cada uma das duas possibilidades de triangulação que divide o quadrilátero em dois triângulos satisfaz a “condição Delaunay”, isto é, que as circunferências de todos os triângulos tenham interiores vazios. Considerando que as circunferências são esferas, a noção de Triangulação de Delaunay estende-se a três dimensões. Generalizações são possíveis para métricas diferentes das Euclidianas. Entretanto, nestes casos não se pode garantir a existência ou a unicidade da Triangulação de Delaunay.

Relação com o Diagrama de Voronoi[editar | editar código-fonte]

A triangulação de um conjunto discreto de pontos P corresponde ao grafo dual do Diagrama de Voronoi para P. Casos especiais incluem a existência de três pontos colineares e quatro pontos cocirculares.

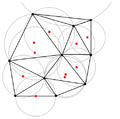
A Triangulação de Delaunay com todas as circunferências e seus centros (em vermelho).
Conectando-se os centros das circunferências produz-se o Diagrama de Voronoi (em vermelho).

Delaunay d-dimensional[editar | editar código-fonte]

Para um conjunto P de pontos no (d-dimensional) espaço Euclidiano, a Triangulação de Delaunay é uma triangulação DT(P) onde nenhum ponto em P está contido dentro do circum-hiperesfera de um simplexo em DT(P). Sabe-se ^[2] que existe uma única triangulação de Delaunay para P, se P é um conjunto de pontos em posição geral; Isto é, não existe k-flat contendo k + 2 pontos nem uma k-esfera contendo k + 3 pontos, para 1 ≤ k ≤ d − 1 (isto é, para um conjunto de pontos no ℝ³ não há três pontos em uma reta, nem quatro em um plano ou círculo, e não há cinco pontos em uma esfera). O problema de encontrar a triangulação de Delaunay de um conjunto de pontos no espaço Euclidiano d-dimensional pode ser convertido para o problema de fecho convexo e um conjunto de pontos em um espaço (d + 1)-dimensional, pela adição de uma coordenada extra a cada ponto p igual a |p|², pegando-se o lado mais baixo do fecho convexo, e mapeando-o de volta para o espaço d-dimensional pela remoção da última coordenada. Assim como o fecho convexo a triangulação também é única, assumindo-se que todas as faces do fecho convexo são simplexos. Faces não simpliciais ocorrem somente quando d + 2 dos pontos originais incidem em uma mesma d-hiperesfera, isto é, se os pontos não estão em posição geral.

Propriedades[editar | editar código-fonte]

Suponha que n seja o número de pontos e d o número de dimensões:

A união de todos os simplexos da triangulação é o fecho convexo dos pontos.
A Triangulação de Delaunay contém O(n^{⌈d / 2⌉}) simplexos.^[3]
No plano (d = 2), se existem b vértices fecho convexo, então qualquer triangulação dos pontos tem no máximo 2n − 2 − b triângulos, mais uma face exterior (veja Características de Euler).
No plano, cada vértice tem em média seis triângulos em sua volta.
No plano, a triangulação de Delaunay maximiza o menor ângulo. Comparada com qualquer outra triangulação de pontos, o menor ângulo na triangulação de Delaunay é pelo menos maior do que o menor ângulo em qualquer outra triangulação. Contudo, a triangulação de Delaunay não necessariamente minimiza o maior ângulo.
Um círculo circunscrevendo qualquer triângulo Delaunay não contém qualquer outro ponto (ou conjunto de pontos) em seu interior.
Se um círculo passando entre dois pontos da entrada de pontos não contém nenhum outro deles em seu interior, então o segmento que conecta os dois pontos é uma aresta da triangulação de Delaunay, para os pontos dados.
A triangulação de Delaunay de um conjunto de pontos em um espaço d-dimensional é a projeção dos pontos do fecho convexo em um parabolóide (d + 1)-dimensional.
O vizinho mais próximo b de qualquer ponto p está na aresta bp da triangulação de Delaunay desde que o grafo do vizinho mais próximo seja um subgrafo da triangulação de Delaunay.

Definição Visual Delaunay: Flipping[editar | editar código-fonte]

Observando-se as propriedades acima, um importante ponto surge: olhando para os dois triângulos ABD e BCD com a aresta BD em comum (veja as figuras), se a soma dos ângulos α e γ for menor ou igual a 180°, os triângulos satisfazem a condição de Delaunay. Esta é uma importante propriedade, pois permite o uso da técnica de flipping. Se dois triângulos não satisfazem a condição de Delaunay, trocando-se a aresta comum BD pela aresta comum AC produz-se dois triângulos que satisfazem a condição Delaunay:

Esta triangulação não satisfaz a condição de Delaunay (a soma de α e γ é maior que 180°).
Esta triangulação não satisfaz a condição de Delaunay (as circunferências contém mais de 3 pontos).
Aplicando Flipping na aresta comum produz-se uma triangulação de Delaunay para os quatro pontos.

Algoritmos[editar | editar código-fonte]

Muitos algoritmos para computar triangulações de Delaunay apoiam-se em operações rápidas para detectar quando um ponto está contido em uma circunferência de algum triângulo e uma eficiente estrutura de dados para armazenamento de triângulos e arestas. Em duas dimensões, uma forma de detectar se um ponto D incide na circunferência de A, B, C é calcular o determinante:^[4]

{\begin{vmatrix}A_{x}&A_{y},&A_{x}^{2}+A_{y}^{2},&1\\[6pt]B_{x}&B_{y},&B_{x}^{2}+B_{y}^{2},&1\\[6pt]C_{x}&C_{y},&C_{x}^{2}+C_{y}^{2},&1\\[6pt]D_{x}&D_{y},&D_{x}^{2}+D_{y}^{2},&1\end{vmatrix}}={\begin{vmatrix}A_{x}-D_{x},&A_{y}-D_{y},&(A_{x}^{2}-D_{x}^{2})+(A_{y}^{2}-D_{y}^{2})\\[6pt]B_{x}-D_{x},&B_{y}-D_{y},&(B_{x}^{2}-D_{x}^{2})+(B_{y}^{2}-D_{y}^{2})\\[6pt]C_{x}-D_{x},&C_{y}-D_{y},&(C_{x}^{2}-D_{x}^{2})+(C_{y}^{2}-D_{y}^{2})\\[6pt]\end{vmatrix}}>0

Quando A, B and C estão ordenados em sentido anti-horário, essa determinante é positiva se e somente se apenas D estiver contido na circunferência.

Algoritmo Flip[editar | editar código-fonte]

Como mencionado acima, se um triângulo é não-Delaunay, podemos rodar uma de suas arestas. Isso nos conduz a um algoritmo simples: construir qualquer triangulação dos pontos, e depois rodar arestas até que nenhum triângulo seja não-Delaunay. Infelizmente, isto pode levar tempo O(n²), e não se estende para 3 ou mais dimensões.^[2]

Incremental[editar | editar código-fonte]

A forma mais simples e eficiente de computar a triangulação de Delaunay é adicionar um vértice de cada vez, triangulando novamente as partes afetadas do grafo a cada adição. Quando um vértice v é adicionado, dividimos em três o triângulo que o contém, então aplicamos o algoritmo flip. Isso irá levar um tempo da ordem de O(n): procuramos por todos os triângulos para encontrar um que contenha v, então fazemos o flip de cada triângulo. Então o tempo final é da ordem de O(n²).

Se inserirmos vértices em uma ordem aleatória, verifica-se (por uma prova um pouco complicada) que cada inserção irá rodar, em média, apenas O(1) triângulos – embora em alguns casos irá rodar muitas vezes mais.^[5] Podemos guardar o histórico das divisões e das rotações realizadas: cada triângulo armazena um ponteiro para os dois ou três triângulos que o substituíram. Para encontrar o triângulo que contém v, começamos por um triângulo raiz, e seguimos o ponteiro que aponta para o triângulo que contém v, até encontrarmos um triângulo que ainda não foi substituído. Em média, isso também levará tempo na ordem de O(n log n).^[2] Para dimensões maiores (provado por Edelsbrunner e Shah^[6]), o tempo de execução pode ser exponencial na ordem da dimensão, mesmo se a triangulação de Delaunay final for pequena.

O algoritmo Bowyer-Watson provê uma outra aproximação para construção incremental. Isso proporciona uma alternativa a rotação de arestas para computar triângulos de Delaunay contendo um novo vértice inserido.

Divisão e Conquista[editar | editar código-fonte]

Um algoritmo de divisão e conquista para triangulações em duas dimensões é um dual de Lee e Schachter que foi aprimorado por Guibas e Stolfi^[7] e, mais tarde, por Dwyer. Nesse algoritmo, uma recursão desenha uma linha para separar os vértices em dois conjuntos. A Triangulação de Delaunay é computada para cada conjunto, e depois os dois conjuntos são unidos ao longo da linha separadora. Utilizando-se alguns truques, a operação de junção pode ser feita em tempo O(n), então o total de tempo gasto em execução é da ordem de O(n log n).^[8]

Para certos tipos de conjuntos de pontos, como uma distribuição aleatória uniforme, pode-se escolher de forma inteligente as linhas separadoras reduzindo o tempo para até O(n log log n) mantendo o pior caso.

Um paradigma de divisão e conquista para triangulação em d dimensões é apresentado em "DeWall: Um rápido algoritmo de divisão e conquista para Triangulação de Delaunay em E^d" por P. Cignoni, C. Montani, R. Scopigno.^[9]

A técnica de divisão e conquista tem se mostrado a mais rápida para a geração de DT.^[10]^[11]

Linha de Varredura[editar | editar código-fonte]

O algoritmo de Fortune utiliza uma técnica de linha de varredura para alcançar complexidade de tempo de O(n log n) em casos planares.

Sweephull[editar | editar código-fonte]

Sweephull^[12] é uma rápida técnica híbrida para Triangulações de Delaunay 2D que utiliza uma propagação radial sweep-hull (sequencialmente criado a partir da ordenação radial do conjunto de pontos 2D, gerando uma triangulação sem sobreposição), pareado com o triângulo da última rodada. Resultados empíricos indicam que o algoritmo roda em aproximadamente metade do tempo do Qhull, e implementações gratuitas podem ser encontradas nas linguagens C++ e C#.^[13]

Aplicações[editar | editar código-fonte]

A árvore geradora mínima euclidiana de um conjunto de pontos é um subconjunto de triangulações de Delaunay dos mesmos pontos, podendo assim ser explorado para computá-la de forma eficiente. Para modelar terrenos ou outros objetos a partir de uma amostra de pontos, a Triangulação de Delaunay nos dá um bom conjunto de triângulos para utilizar como polígonos no modelo. Em particular, a Triangulação de Delaunay evita triângulos magros (possuem circunferências grandes em comparação com suas áreas). Veja Rede Irregular Triangulada.

Triangulações de Delaunay podem ser utilizadas para determinar a densidade ou a intensidade de amostragens de pontos por meio da DTFE.

Triangulações de Delaunay também são muitas vezes utilizadas para construir diagramas para os espaços discretos, como o método dos elementos finitos e o método do volume finito de simulação de física, razão pela qual os algoritmos de triangulação rápida têm sido desenvolvidos. Normalmente, o domínio a ser transformado em diagramas é especificado como um complexo simplicial e grosso; para o diagrama ser numericamente estável, deve ser refinado utilizando-se o algoritmo de Ruppert algorithm.

Ver também[editar | editar código-fonte]

Referências[editar | editar código-fonte]

↑ B. Delaunay: Sur la sphère vide, Izvestia Akademii Nauk SSSR, Otdelenie Matematicheskikh i Estestvennykh Nauk, 7:793–800, 1934
↑ ^a ^b ^c de Berg, Mark; Otfried Cheong, Marc van Kreveld, Mark Overmars (2008). Computational Geometry: Algorithms and Applications (PDF). [S.l.]: Springer-Verlag. ISBN 978-3-540-77973-5
↑ Seidel, R. (1995). «The upper bound theorem for polytopes: an easy proof of its asymptotic version». Computational Geometry. 5 (2): 115–116. doi:10.1016/0925-7721(95)00013-Y
↑ Guibas, Lenoidas; Stolfi, Jorge (1 de abril de 1985). «Primitives for the manipulation of general subdivisions and the computation of Voronoi». ACM. p. 107. Consultado em 1 de agosto de 2009
↑ Guibas, L.; D. Knuth; M. Sharir (1992). «Randomized incremental construction of Delaunay and Voronoi diagrams». Algorithmica. 7: 381–413. doi:10.1007/BF01758770 ^{[ligação inativa]}
↑ Edelsbrunner, Herbert; Nimish Shah (1996). «Incremental Topological Flipping Works for Regular Triangulations». Algorithmica. 15 (3): 223–241. doi:10.1007/BF01975867 ^{[ligação inativa]}
↑ «Computing Constrained Delaunay Triangulations». Consultado em 13 de novembro de 2011. Cópia arquivada em 22 de setembro de 2017
↑ G. Leach: Improving Worst-Case Optimal Delaunay Triangulation Algorithms. June 1992
↑ Cignoni, P.; C. Montani; R. Scopigno (1998). «DeWall: A fast divide and conquer Delaunay triangulation algorithm in E^d». Computer-Aided Design. 30 (5): 333–341. doi:10.1016/S0010-4485(97)00082-1
↑ A Comparison of Sequential Delaunay Triangulation Algorithms http://www.cs.berkeley.edu/~jrs/meshpapers/SuDrysdale.pdf
↑ http://www.cs.cmu.edu/~quake/tripaper/triangle2.html
↑ S-hull
↑ http://www.s-hull.org/

Ligações externas[editar | editar código-fonte]

Delaunay triangulation in CGAL, the Computational Geometry Algorithms Library:
- Yvinec, Mariette. «2D Triangulation». Consultado em 1 de abril de 2010
- Pion, Sylvain; Teillaud, Monique. «3D Triangulations». Consultado em 1 de abril de 2010
- Hert, Susan; Seel, Michael. «dD Convex Hulls and Delaunay Triangulations». Consultado em 1 de abril de 2010
«Delaunay triangulation». Wolfram MathWorld. Consultado em 1 de abril de 2010
«Qhull». Consultado em 1 de abril de 2010 — Code for Convex Hull, Delaunay Triangulation, Voronoi Diagram, and Halfspace Intersection
Shewchuk, Jonathan Richard. «Triangle». Consultado em 1 de abril de 2010 – A Two-Dimensional Quality Mesh Generator and Delaunay Triangulator
Kumar, Piyush; Mohanty, Somya. «Triangle++» – A C++ wrapper on Triangle
«Poly2Tri». Google Code. Consultado em 1 de abril de 2010 – A sweepline Constrained Delaunay Triangulation (CDT) library, available in ActionScript 3, C, C++, C#, Go, Java, Javascript, Python and Ruby

[Delaunay1934-1] B. Delaunay: Sur la sphère vide, Izvestia Akademii Nauk SSSR, Otdelenie Matematicheskikh i Estestvennykh Nauk, 7:793–800, 1934

[deBerg-2] Berg, Mark; Otfried Cheong, Marc van Kreveld, Mark Overmars (2008). Computational Geometry: Algorithms and Applications (PDF). [S.l.]: Springer-Verlag. ISBN 978-3-540-77973-5

[3] Seidel, R. (1995). «The upper bound theorem for polytopes: an easy proof of its asymptotic version». Computational Geometry. 5 (2): 115–116. doi:10.1016/0925-7721(95)00013-Y

[4] Guibas, Lenoidas; Stolfi, Jorge (1 de abril de 1985). «Primitives for the manipulation of general subdivisions and the computation of Voronoi». ACM. p. 107. Consultado em 1 de agosto de 2009

[5] Guibas, L.; D. Knuth; M. Sharir (1992). «Randomized incremental construction of Delaunay and Voronoi diagrams». Algorithmica. 7: 381–413. doi:10.1007/BF01758770 ^{[ligação inativa]}

[6] Edelsbrunner, Herbert; Nimish Shah (1996). «Incremental Topological Flipping Works for Regular Triangulations». Algorithmica. 15 (3): 223–241. doi:10.1007/BF01975867 ^{[ligação inativa]}

[7] «Computing Constrained Delaunay Triangulations». Consultado em 13 de novembro de 2011. Cópia arquivada em 22 de setembro de 2017

[Leach1992-8] G. Leach: Improving Worst-Case Optimal Delaunay Triangulation Algorithms. June 1992

[9] Cignoni, P.; C. Montani; R. Scopigno (1998). «DeWall: A fast divide and conquer Delaunay triangulation algorithm in E^d». Computer-Aided Design. 30 (5): 333–341. doi:10.1016/S0010-4485(97)00082-1

[10] A Comparison of Sequential Delaunay Triangulation Algorithms http://www.cs.berkeley.edu/~jrs/meshpapers/SuDrysdale.pdf

[11] ttp://www.cs.cmu.edu/~quake/tripaper/triangle2.html

[12] S-hull

[13] ttp://www.s-hull.org/

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]