Determinante

Parte da série sobre
Matemática
História
Áreas Teoria dos números Geometria Álgebra Cálculo e Análise Matemática discreta Lógica matemática e Teoria dos conjuntos Probabilidade Estatística e Teoria da decisão Relação com as ciências Física Química Computação Biologia Linguística Economia Filosofia Educação
Portal da Matemática

Em matemática, determinante é uma função matricial que associa a cada matriz quadrada um escalar, ou seja, é uma função que transforma uma matriz quadrada em um número real. Esta função permite saber se a matriz tem ou não inversa, pois as que não têm são precisamente aquelas cujo determinante é igual a 0. O determinante de uma matriz $A$ é denotado por $\det(A)$, $\det A$ ou $|A|$.

Para as matrizes de ordem 1, o valor do determinante é o próprio elemento: $\det {\begin{pmatrix}a_{11}\end{pmatrix}}=a_{11}$.

No caso de matrizes de ordem 2, multiplicam-se os elementos da diagonal principal e diminui-se do resultado a multiplicação dos elementos da diagonal secundária, ou seja:

$$\det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.$$

Para matrizes de ordem 3, pode ser utilizada a Regra de Sarrus, a qual fornece:

$$\det {\begin{pmatrix}a&b&c\\d&e&f\\g&h&i\end{pmatrix}}={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=(aei+bfg+cdh)-(afh+bdi+ceg).$$

De modo geral, para uma matriz de ordem $n$, com $n\geq 2$, pode-se utilizar de dois outros processos, conhecidos como fórmula de Laplace e fórmula de Leibniz para determinantes.

Geometricamente, o determinante pode ser visto como o fator de escala de volume da transformação linear descrita por uma matriz. Este também é o volume com sinal do paralelepípedo n-dimensional gerado pelos vetores coluna ou linha da matriz. O determinante é positivo ou negativo, dependendo de o mapeamento linear preservar ou reverter a orientação do espaço n-dimensional.

Determinantes aparecem em várias áreas da matemática. Por exemplo, uma matriz é frequentemente usada para representar os coeficientes em um sistema de equações lineares, e o determinante pode ser usado para resolver essas equações no caso de sistemas com o mesmo número de variáveis e de equações (se o determinante da matriz dos coeficientes for um valor diferente de zero, o sistema possui uma única solução; caso o valor do determinante seja zero, o sistema é possível indeterminado ou impossível), embora outros métodos de solução sejam muito mais eficientes em termos computacionais. Ainda na álgebra linear, uma matriz (com entradas em um corpo) é singular (não invertível) se, e somente se, seu determinante for zero. Isso leva ao uso de determinantes na definição do polinômio característico de uma matriz, cujas raízes são os autovalores. Os determinantes também utilizados para cálculos relacionados à independência linear e dão a orientação de uma base em um espaço vetorial.

Na geometria analítica, os determinantes expressam os volumes n-dimensionais com sinal dos paralelepípedos n-dimensionais. Isso leva ao uso de determinantes no cálculo, com o determinante da matriz jacobiana na regra de mudança de variáveis ​​para integrais de funções de várias variáveis. Determinantes aparecem frequentemente em identidades algébricas, como a identidade de Vandermonde. Também aparecem no cálculos de circulantes.

Os determinantes possuem muitas propriedades algébricas. Uma delas é a multiplicatividade, a saber, que o determinante de um produto de matrizes é igual ao produto dos determinantes das matrizes. Tipos especiais de matrizes têm determinantes especiais; por exemplo, o determinante de uma matriz ortogonal é sempre $\pm 1$, e o determinante de uma matriz hermitiana complexa é sempre real.

Definição

Supondo que $A$ é uma matriz quadrada com $n$ linhas e $n$ colunas, ou seja,

$A={\begin{bmatrix}a_{1,1}&a_{1,2}&\dots &a_{1,n}\\a_{2,1}&a_{2,2}&\dots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\dots &a_{n,n}\end{bmatrix}},$

o determinante de $A$ pode ser indicado por $\det A$ ou diretamente em termos das entradas da matriz, escrevendo-se barras em vez de colchetes:

$\det A={\begin{vmatrix}a_{1,1}&a_{1,2}&\dots &a_{1,n}\\a_{2,1}&a_{2,2}&\dots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\dots &a_{n,n}\end{vmatrix}}.$

Existem várias maneiras equivalentes de definir o determinante de $A$. Talvez a maneira mais simples de definir o determinante seja de maneira recursiva considerando os elementos na primeira linha os respectivos menores: começando pela esquerda, multiplica-se o primeiro elemento pelo menor, subtrai-se o produto do próximo elemento e seu menor e segue-se adicionando e subtraindo alternadamente esses produtos até que todos os elementos na linha estejam esgotados. Por exemplo, para o caso de uma matriz de ordem 4:

${\begin{vmatrix}a&b&c&d\\e&f&g&h\\i&j&k&l\\m&n&o&p\end{vmatrix}}=a\,{\begin{vmatrix}f&g&h\\j&k&l\\n&o&p\end{vmatrix}}-b\,{\begin{vmatrix}e&g&h\\i&k&l\\m&o&p\end{vmatrix}}+c\,{\begin{vmatrix}e&f&h\\i&j&l\\m&n&p\end{vmatrix}}-d\,{\begin{vmatrix}e&f&g\\i&j&k\\m&n&o\end{vmatrix}}.$

Assim, para o procedimento acima ser consistente, basta definir o determinante de uma matriz de ordem 1 como a própria entrada da matriz. Para uma matriz de ordem 3, tem-se

$|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=a\,{\begin{vmatrix}\Box &\Box &\Box \\\Box &e&f\\\Box &h&i\end{vmatrix}}-b\,{\begin{vmatrix}\Box &\Box &\Box \\d&\Box &f\\g&\Box &i\end{vmatrix}}+c\,{\begin{vmatrix}\Box &\Box &\Box \\d&e&\Box \\g&h&\Box \end{vmatrix}}=a\,{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}=aei+bfg+cdh-ceg-bdi-afh.$

O procedimento acima é um caso particular da fórmula (ou teorema) de Laplace. O determinante de uma matriz de tamanho arbitrário também pode ser definido pela fórmula de Leibniz para determinantes. A fórmula de Leibniz para o determinante de uma matriz de ordem $n$ é

$\det(A)=\sum _{\sigma \in S_{n}}\left(\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}\right),$

onde a soma é computada sobre todas as permutações σ do conjunto $\{1,2,3,...,n\}$. A permutação é uma função que reordena esse conjunto de inteiros. O valor da i-ésima posição depois da reordenação $\sigma$ é denotado por $\sigma _{i}$. Por exemplo, para $n=3$, a sequência original $1,2,3$ pode ser reordenada para $\sigma =[2,3,1]$, com $\sigma _{1}=2$, $\sigma _{2}=3$, $\sigma _{3}=1$. O conjunto de todas essas permutações é denotado por $S_{n}$. Para cada permutação $\sigma$, $\operatorname {sgn}(\sigma )$ denota o sinal de $\sigma$, que tem valor +1 sempre que a reordenação dada por $\sigma$ puder ser alcançada através da troca sucessiva de duas entradas um número par de vezes, e valor -1 sempre que puder ser alcançada por um número ímpar dessas trocas.

Em qualquer um dos $n!$ termos da soma,

$\prod _{i=1}^{n}a_{i,\sigma _{i}}$

é a notação para o produto das entradas nas posições $(i,\sigma _{i})$, onde $i$ varia de $1$ para $n$:

$a_{1,\sigma _{1}}\cdot a_{2,\sigma _{2}}\cdots a_{n,\sigma _{n}}.$

Por exemplo, para o determinante de uma matriz $A$ 3 × 3 (n = 3) tem-se:

${\begin{aligned}\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}&={}\operatorname {sgn}([1,2,3])\prod _{i=1}^{n}a_{i,[1,2,3]_{i}}+\operatorname {sgn}([1,3,2])\prod _{i=1}^{n}a_{i,[1,3,2]_{i}}+\operatorname {sgn}([2,1,3])\prod _{i=1}^{n}a_{i,[2,1,3]_{i}}\\&+{}\operatorname {sgn}([2,3,1])\prod _{i=1}^{n}a_{i,[2,3,1]_{i}}+\operatorname {sgn}([3,1,2])\prod _{i=1}^{n}a_{i,[3,1,2]_{i}}+\operatorname {sgn}([3,2,1])\prod _{i=1}^{n}a_{i,[3,2,1]_{i}}\\&={}\prod _{i=1}^{n}a_{i,[1,2,3]_{i}}-\prod _{i=1}^{n}a_{i,[1,3,2]_{i}}-\prod _{i=1}^{n}a_{i,[2,1,3]_{i}}+\prod _{i=1}^{n}a_{i,[2,3,1]_{i}}+\prod _{i=1}^{n}a_{i,[3,1,2]_{i}}-\prod _{i=1}^{n}a_{i,[3,2,1]_{i}}\\[2pt]&={}a_{1,1}a_{2,2}a_{3,3}-a_{1,1}a_{2,3}a_{3,2}-a_{1,2}a_{2,1}a_{3,3}+a_{1,2}a_{2,3}a_{3,1}+a_{1,3}a_{2,1}a_{3,2}-a_{1,3}a_{2,2}a_{3,1}.\end{aligned}}$

História

Historicamente , os determinantes eram usados muito antes das matrizes: originalmente, um determinante era definido como uma propriedade de um sistema de equações lineares. O determinante identifica se o sistema possui uma solução exclusiva (que ocorre precisamente se o determinante da matriz dos coeficientes for diferente de zero).

Os determinantes foram usados pela primeira vez no livro de matemática chinês Os nove capítulos da arte matemática (estudiosos chineses, por volta do século III a.C.). Na Europa, os determinantes de matriz de ordem 2 foram estudados por Cardano no final do século XVI e os maiores por Leibniz.

No Japão, Seki Takakazu é creditado pela descoberta do resultante e do determinante (inicialmente em 1683, mas a versão completa até 1710). Na Europa, Cramer (1750) acrescentou à teoria, relacionando o determinante a conjuntos de equações. A lei de recorrência foi anunciada pela primeira vez por Bézout (1764).

Foi Vandermonde (1771) quem primeiro reconheceu os determinantes em relação a funções independentes. Laplace (1772) desenvolveu o método geral ao expandir um determinante em termos de seus menores complementares, onde Vandermonde já havia apresentado um caso especial. Imediatamente depois, Lagrange (1773) tratou determinantes de segunda e terceira ordem, provando muitos casos especiais de identidades gerais.

Gauss (1801) fez o próximo avanço. Como Lagrange, ele usou muito os determinantes na teoria dos números. Ele introduziu a palavra determinante (Laplace usara resultante), embora não fosse com o significado atual. Gauss também chegou à noção de inverso do determinante e chegou muito perto do teorema da multiplicação.

O próximo colaborador de importância é Binet (1811, 1812), que declarou formalmente o teorema relativo ao produto de duas matrizes de m colunas e n linhas, o que para o caso especial de m = n se reduz ao teorema da multiplicação. No mesmo dia (30 de novembro de 1812) em que Binet apresentou seu trabalho à Academia, Cauchy também apresentou um trabalho sobre o assunto (veja a fórmula de Cauchy-Binet). Neste, inicia-se a teoria em sua generalidade, com o uso da palavra determinante em seu sentido atual, o resumo e a simplificação do que era então conhecido sobre o assunto, a melhora da notação e a apresentação de uma prova mais satisfatória que a realizada por Bineta para o teorema da multiplicação.

A próxima figura importante foi Jacobi (de 1827). Ele usou o determinante funcional, o qual Sylvester mais tarde chamou de jacobiano e, em suas memórias no Crelle's Journal de 1841, tratou especialmente desse determinante funcional. Da mesma forma, tratou sobre a classe de funções alternadas, as quais Sylvester chamou de alternantes. Na época das últimas memórias de Jacobi, Sylvester (1839) e Cayley começaram seus trabalhos.

O estudo de formas especiais de determinantes tem sido o resultado natural da complementação da teoria geral. Determinantes axissimétricos foram estudados por Lebesgue, Hesse e Sylvester; determinantes persimétricos por Sylvester e Hankel; circulantes por Catalan, Spottiswoode, Glaisher e Scott; determinantes de inclinação e Pfaffians, em conexão com a teoria da transformação ortogonal, por Cayley; continuantes por Sylvester; wronskianos (assim chamados por Muir) por Christoffel e Frobenius; determinantes compostos por Sylvester, Reiss e Picquet; jacobianos e hessianos por Sylvester; e determinantes simétricos por Trudi. Dos livros didáticos sobre o assunto, Spottiswoode foi o primeiro. Nos Estados Unidos, Hanus (1886), Weld (1893) e Muir/Metzler (1933) publicaram dissertações.

Propriedades

1. O determinante da matriz identidade é igual a $1$:
      $\left|I_{n}\right|=1$;
2. O determinante de uma matriz é igual ao determinante da sua transposta:
      $\left|A\right|=\left|A^{T}\right|$;
3. Se uma matriz quadrada é invertível então, o determinante da sua inversa é o inverso do seu determinante:
      $\left|A^{-1}\right|={\frac {1}{\left|A\right|}}.$ Resulta desta propriedade que para matrizes invertíveis o determinante não pode ser nulo;
4. O determinante do produto de matrizes quadradas de mesma ordem é o produto dos determinantes (teorema de Binet):
      $\left|AB\right|=\left|A\right|\left|B\right|$
5. O determinante da multiplicação de um escalar por uma matriz quadrada de ordem $n$ é igual a esse escalar, elevado a $n$, vezes o determinante dessa matriz:
      $\left|\lambda A\right|=\lambda ^{n}\left|A\right|,$ onde $n$ é a ordem da matriz $A$
6. Se $A$ é ortogonal, então $\left|A\right|=\pm 1$;
7. Se uma matriz é triangular (superior ou inferior) o seu determinante é o produto dos elementos da diagonal principal:
      Seja $A$ uma matriz triangular de ordem $n,$ então $\left|A\right|=a_{1,1}a_{2,2}\cdots a_{n,n}=\prod _{i=1}^{n}a_{i,i}$;
8. Se uma fila (linha ou coluna) da matriz $A$ é composta de zeros, então $\left|A\right|=0$;
9. Se cada elemento de uma linha (ou coluna) de $A$ for escrito como soma de duas parcelas; então $\left|A\right|$ é a soma de dois determinantes de ordem $n$, cada um considerando como elemento daquela linha (ou coluna) uma das parcelas, sendo repetidas as demais linhas (ou colunas);
10. Se uma fila (linha ou coluna) de uma matriz $A$ é multiplicada por um escalar $\lambda ,$ então o determinante da nova matriz é igual ao determinante de $A$ multiplicado por $\lambda$;
11. Se duas linhas (ou colunas) de $A$ são permutadas, então o determinante da nova matriz é $-\left|A\right|$;
12. Se $A$ tem duas linhas (ou colunas) iguais, então $\left|A\right|=0$;
13. Dadas as matrizes $A$ e $B$ quadradas, de ordem $n$, com elementos diferentes apenas na fila $j$. O determinante de $C$, matriz quadrada de ordem $n$, onde a sua fila $j$ é a soma dos elementos da filas $j$ de $A$ e de $B$ é igual ao determinante de $A$ somado ao determinante de $B$ ($\det C=\det A+\det B$);
14. Se for somado, a uma linha (ou coluna) de $A$, um múltiplo de outra linha (ou coluna), o determinante da nova matriz é igual ao de $A$ (essa propriedade também é conhecida como Teorema de Jacobi).

Regra de Chiò

O teorema de Jacobi (propriedade 14 acima) ajuda na formulação da regra de Chiò, que permite reduzir em um a ordem da matriz e facilitar o cálculo do determinante. A regra consiste em suprimir a primeira linha e a primeira coluna de uma matriz $A$, cujo elemento $a_{11}$ é igual a $1$ e, para cada elemento restante, subtrair o produto dos elementos nas extremidades das linha e coluna suprimidas, ou seja, substituir por: $a_{nn}-(a_{n1}\cdot a_{1n})$. A nova matriz possui o mesmo determinante que a anterior:

$\det A=\det {\begin{pmatrix}1&a_{12}&a_{13}&\dots &a_{1n}\\a_{21}&a_{22}&a_{23}&\dots &a_{2n}\\a_{31}&a_{32}&a_{33}&\dots &a_{3n}\\\vdots &\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&a_{n3}&\dots &a_{nn}\end{pmatrix}}=\det {\begin{pmatrix}a_{22}-(a_{21}\cdot a_{12})&a_{23}-(a_{21}\cdot a_{13})&\dots &a_{2n}-(a_{21}\cdot a_{1n})\\a_{32}-(a_{31}\cdot a_{12})&a_{33}-(a_{31}\cdot a_{13})&\dots &a_{3n}-(a_{31}\cdot a_{1n})\\\vdots &\vdots &\ddots &\vdots \\a_{n2}-(a_{n1}\cdot a_{12})&a_{n3}-(a_{n1}\cdot a_{13})&\dots &a_{nn}-(a_{n1}\cdot a_{1n})\end{pmatrix}}$

No caso de a matriz $A$ não ter $a_{11}=1$, pode-se utilizar as propriedades 10, 11 ou 14 para se obter uma nova matriz cujo elemento da primeira linha e da primeira coluna é $1$.

Complemento de Schur

A identidade a seguir vale para um complemento Schur de uma matriz quadrada. O complemento de Schur surge como resultado da eliminação gaussiana em blocos, ao se multiplicar uma matriz $M$, pela direita, por uma matriz triangular inferior em bloco

$L=\left[{\begin{matrix}I_{p}&0\\-D^{-1}C&I_{q}\end{matrix}}\right].$

Aqui $I_{p}$ indica a matriz identidade $p\times p$. Após multiplicação com a matriz $L$, o complemento de Schur aparece no bloco superior $p\times p$. A matriz produto é

${\begin{aligned}ML&=\left[{\begin{matrix}A&B\\C&D\end{matrix}}\right]\left[{\begin{matrix}I_{p}&0\\-D^{-1}C&I_{q}\end{matrix}}\right]=\left[{\begin{matrix}A-BD^{-1}C&B\\0&D\end{matrix}}\right]=\left[{\begin{matrix}I_{p}&BD^{-1}\\0&I_{q}\end{matrix}}\right]\left[{\begin{matrix}A-BD^{-1}C&0\\0&D\end{matrix}}\right].\end{aligned}}$

Ou seja, foi efetuada uma decomposição gaussiana

$\left[{\begin{matrix}A&B\\C&D\end{matrix}}\right]=\left[{\begin{matrix}I_{p}&BD^{-1}\\0&I_{q}\end{matrix}}\right]\left[{\begin{matrix}A-BD^{-1}C&0\\0&D\end{matrix}}\right]\left[{\begin{matrix}I_{p}&0\\D^{-1}C&I_{q}\end{matrix}}\right],$

de modo que, como a primeira e a terceira matrizes que aparecem no lado direito da igualdade têm determinante igual a 1,

${\det }{\begin{bmatrix}A&B\\C&D\end{bmatrix}}={\det }(D)\,{\det }\left(A-BD^{-1}C\right)={\det }\left(AD-BC\right).$

Essa é a fórmula do determinante de Schur.

Teorema do determinante de Sylvester

Sylvester's determinant theorem states that for A, an m × n matrix, and B, an n × m matrix (so that A and B have dimensions allowing them to be multiplied in either order forming a square matrix):O teorema do determinante de Sylvester afirma que para uma matriz $A$, $m\times n$, e uma uma matriz $B$, $n\times m$, (de modo que $A$ e $B$ tenham dimensões que permitam que sejam multiplicadas em qualquer ordem, formando uma matriz quadrada):

$\det \left(I_{\mathit {m}}+AB\right)=\det \left(I_{\mathit {n}}+BA\right),$

onde $I_{m}$ e $I_{n}$ são as matrizes identidade de ordens $m$ e $n$, respectivamente. A partir deste resultado geral, seguem várias consequências:

• Para o caso de um vetor coluna $c$ e de vetor de linha $r$, cada um com $m$ componentes, a fórmula permite o cálculo rápido do determinante de uma matriz que difere da matriz de identidade por uma matriz de posto 1:

$\det \left(I_{\mathit {m}}+cr\right)=1+rc;$

• De modo mais geral, para qualquer matriz invertível $X$, de ordem $m$:

$\det(X+AB)=\det(X)\det \left(I_{\mathit {n}}+BX^{-1}A\right);$

• Para vetores coluna e linha, como os acima:

$\det(X+cr)=\det(X)\det \left(1+rX^{-1}c\right);$

• Para matrizes quadradas A e B do mesmo tamanho, as matrizes AB e BA têm os mesmos polinômios característicos e, portanto, os mesmos autovalores.

Cálculo de determinantes

Determinante de uma matriz de ordem 1

O determinante da matriz $A$ de ordem $n=1,$ é o própria entrada da matriz, ou seja, para uma matriz quadrada $A=[a_{11}]$, tem-se $\det(A)=a_{11}$. Por exemplo, para

$$A=(3),$$

segue que $\det(A)=3.$

Determinante de uma matriz de ordem 2

A área do paralelogramo é o valor absoluto do determinante da matriz formada pelos vetores que representam seus lados

O determinante de uma matriz de ordem 2 é a diferença entre o produto dos termos da diagonal principal e o produto dos termos da diagonal secundária:

$$\det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}=ad-bc.$$

Por exemplo, o determinante da matriz ${\begin{pmatrix}0&2\\1&-1\end{pmatrix}}$ é dado por: $0\cdot (-1)-2\cdot 1=0-2=-2.$

Determinante de uma matriz de ordem 3

Regra de Sarrus: esquema de memorização paro o cálculo do determinante de uma matriz 3x3

Para calcular o determinante de matrizes de ordem 3, geralmente é utilizada a regra de Sarrus. O determinante é dado por

$$\det {\begin{pmatrix}a&b&c\\d&e&f\\g&h&i\end{pmatrix}}=(aei+bfg+cdh)-(afh+bdi+ceg).$$

Por exemplo, para a matriz

$$A={\begin{pmatrix}1&3&10\\-1&1&10\\0&2&10\end{pmatrix}},$$

inicialmente são copiadas as duas primeiras colunas da matriz à direita da terceira coluna, de modo que seja obtida uma sequência de cinco colunas

$${\begin{vmatrix}1&3&10\\-1&1&10\\0&2&10\end{vmatrix}}{\begin{matrix}1&3\\-1&1\\0&2\end{matrix}}.$$

Em seguida, são somados os produtos das três diagonais que partem de cima para baixo e subtraídos os produtos das três diagonais que vão de baixo para cima, obtendo-se:

$$\det(A)=(1)(1)(10)+(3)(10)(0)+(10)(-1)(2)-(1)(10)(2)-(3)(-1)(10)-(10)(1)(0)=10+0+(-20)-20-(-30)-0=0.$$

O volume deste paralelepípedo é o valor absoluto do determinante da matriz formada pelas linhas construídas a partir dos vetores $r_{1},r_{2}$e$r_{3}$.

Determinantes de matrizes de ordem maior que 3

Para o cálculo de determinantes de matrizes quadradas de ordem superior ou igual a 2 pode ser utilizado o teorema de Laplace. Esse teorema estabelece o seguinte:

O determinante de uma matriz é igual à soma dos produtos dos elementos de qualquer linha ou coluna pelos respectivos complementos algébricos(cofatores matriciais).

O complemento algébrico de um elemento $a_{i,j}$ de uma matriz $A$ é o número $A_{i,j}=(-1)^{i+j}\,C_{i,j},$ sendo $C_{i,j}$ o determinante da matriz que se obtém eliminando da matriz original a linha $i$ e a coluna $j$.

Na prática, o uso do teorema de Laplace equivale a reduzir o cálculo do determinante de uma matriz de ordem $n$ ao cálculo de determinantes de matrizes de ordem $n-1$, podendo ser aplicado quantas vezes forem necessárias até serem obtidos determinantes mais fáceis de se calcular (de matrizes de ordem 2 ou 3). Fixando-se a linha $i$, o teorema pode ser expresso pela fórmula:

$\det(A)=\sum _{j=1}^{n}\,a_{i,j}\,A_{i,j}$

ou, fixando-se a coluna $j$:

$\det(A)=\sum _{i=1}^{n}\,a_{i,j}\,A_{i,j}$,

onde $n$ é a ordem da matriz. A escolha da linha ou coluna da matriz para a aplicação do processo é indiferente; contudo, para maior simplicidade dos cálculos, convém escolher a linha ou coluna que contiver mais zeros.

Outra alternativa para o cálculo de determinantes de matrizes de qualquer ordem é a fórmula de Leibniz para determinantes. No entanto, assim como a aplicação do teorema de Laplace, essa opção é inviável para se trabalhar com matrizes de grande porte, sendo preferível, especialmente do ponto de vista computacional, o processo de triangularização de matrizes (eliminação gaussiana).

Exemplo: aplicação do teorema de Laplace a uma matriz 4x4

Considerando a matriz

$$A={\begin{pmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\a_{21}&a_{22}&a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41}&a_{42}&a_{43}&a_{44}\end{pmatrix}}$$

e desenvolvendo o determinante pela primeira linha, obtém-se:

$$\det A=a_{11}A_{1,1}+a_{12}A_{1,2}+a_{13}A_{1,3}+a_{14}A_{1,4},$$

onde $A_{i,j}$ representa o cofator referente ao termo $a_{i,j}$. Expandindo, chega-se a

$\det A=a_{11}(-1)^{2}{\begin{vmatrix}a_{22}&a_{23}&a_{24}\\a_{32}&a_{33}&a_{34}\\a_{42}&a_{43}&a_{44}\end{vmatrix}}+a_{12}(-1)^{3}{\begin{vmatrix}a_{21}&a_{23}&a_{24}\\a_{31}&a_{33}&a_{34}\\a_{41}&a_{43}&a_{44}\end{vmatrix}}+a_{13}(-1)^{4}{\begin{vmatrix}a_{21}&a_{22}&a_{24}\\a_{31}&a_{32}&a_{34}\\a_{41}&a_{42}&a_{44}\end{vmatrix}}+a_{14}(-1)^{5}{\begin{vmatrix}a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\a_{41}&a_{42}&a_{43}\end{vmatrix}}$,

ou seja, é necessário o cálculo de quatro determinantes de matrizes de ordem 3 (a não ser que algum dos termos da primeira linha de $A$ seja zero):

${\begin{aligned}\det A&=a_{11}(a_{22}a_{33}a_{44}+a_{32}a_{43}a_{24}+a_{42}a_{23}a_{34}-a_{24}a_{33}a_{42}-a_{22}a_{43}a_{34}-a_{23}a_{32}a_{44})\\&-a_{12}(a_{21}a_{33}a_{44}+a_{31}a_{43}a_{24}+a_{41}a_{23}a_{34}-a_{24}a_{33}a_{41}-a_{34}a_{43}a_{21}-a_{44}a_{31}a_{23})\\&+a_{13}(a_{21}a_{31}a_{44}+a_{31}a_{42}a_{24}+a_{41}a_{22}a_{34}-a_{24}a_{32}a_{41}-a_{34}a_{42}a_{21}-a_{44}a_{31}a_{22})\\&-a_{14}(a_{21}a_{32}a_{43}+a_{31}a_{42}a_{23}+a_{41}a_{22}a_{33}-a_{23}a_{32}a_{41}-a_{33}a_{42}a_{21}-a_{43}a_{31}a_{22})\end{aligned}}$.

Cálculo de determinantes por triangularização de matrizes

Uma forma mais simples de calcular o determinante de matrizes de grande porte é fazer o uso de algumas propriedades, de modo a reescrever uma matriz de modo que o determinante possa, em seguida, ser calculado imediatamente. Tendo em vista a propriedade 5, que afirma que o determinante de uma matriz triangular é igual ao seu termo principal (produto dos elementos da diagonal principal), a ideia é aplicar outras propriedades nas linhas (ou colunas) da matriz, de modo a triangularizá-la (transformá-la em uma matriz triangular). Este processo é conhecido como triangularização de matrizes, sendo equivalente ao processo de eliminação gaussiana. Para tal, observam-se as seguintes propriedades, conhecidas como operações elementares sobre as linhas de uma matriz, as quais podem ou não alterar o determinante:

• Permutar linhas troca o sinal do determinante (propriedade 11);
• Multiplicar uma linha por um número real $\lambda$ não nulo, multiplica o determinante por $\lambda$ (propriedade 10);
• Somar a uma linha um múltiplo de outra linha não altera o determinante (propriedade 14).

Para triangularizar a matriz basta atentar para as possíveis compensações, no determinante, provocadas pelas operações elementares utilizadas, não havendo uma única maneira de realizar esse processo. O método é algorítmico, constituído da seguinte ideia: a cada coluna, da primeira à penúltima, deve-se obter zeros nas posições abaixo da diagonal principal. Veja o exemplo a seguir:

Exemplos

• Nota-se que

${\begin{vmatrix}2&-4&8\\5&4&6\\-3&0&2\end{vmatrix}}=2{\begin{vmatrix}1&-2&4\\5&4&6\\-3&0&2\end{vmatrix}}=2{\begin{vmatrix}1&-2&4\\0&14&-14\\0&-6&14\end{vmatrix}}=(2)(14){\begin{vmatrix}1&-2&4\\0&1&-1\\0&-6&14\end{vmatrix}}=(2)(14){\begin{vmatrix}1&-2&4\\0&1&-1\\0&0&8\end{vmatrix}}=2\cdot 14\cdot 1\cdot 1\cdot 8=224$,

onde foram feitas, respectivamente, as seguintes operações elementares nas linhas:

$$L_{1}\leftarrow {\frac {1}{2}}L_{1},L_{2}\leftarrow L_{2}-5.L_{1}\land L_{3}\leftarrow L_{3}+3.L_{1},L_{2}\leftarrow {\frac {1}{14}}L_{2},L_{3}\leftarrow L_{3}+6.L_{2},$$

sendo a notação $L_{i}\leftarrow \Box$ usada para indicar que a linha $i$ foi substituída pela combinação de linhas $\Box$.

• O determinante da matriz

$A={\begin{bmatrix}-2&2&-3\\-1&1&3\\2&0&-1\end{bmatrix}}$

pode ser calculado a partir das seguintes matrizes:

$B={\begin{bmatrix}-2&2&-3\\0&0&4.5\\2&0&-1\end{bmatrix}},\quad C={\begin{bmatrix}-2&2&-3\\0&0&4.5\\0&2&-4\end{bmatrix}},\quad D={\begin{bmatrix}-2&2&-3\\0&2&-4\\0&0&4.5\end{bmatrix}}.$

Aqui, $B$ é obtida a partir de $A$ pela adição de −1/2 vezes a primeira linha na segunda linha, de modo que $\det B=\det A$. A matriz $C$ é obtida a partir de $B$ pela adição da terceira linha à primeira, de modo que $\det C=\det B$. Finalmente, a matriz $D$ é obtida a partir de $C$ pela permuta entre as linhas 2 e 3, de modo que $\det D=-\det C$. Como $D$ é uma matriz triangular superior, o seu determinante é igual ao termo principal: $(-2)\cdot 2\cdot 4,5=-18$. Portanto, $\det A=-\det D=18$.

Determinantes e autovalores

Se $A$ é uma matriz, de ordem $n$, cujas entradas são números complexos e cujos $n$ autovalores são $\lambda _{1},\lambda _{2},\ldots ,\lambda _{n}$, então o determinante de $A$ é o produto dos $n$ autovalores:

$\det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.$

O produto de todos os autovalores diferentes de zero é chamado de pseudo-determinante.

Por outro lado, os determinantes podem ser usados para encontrar os autovalores da matriz $A$: são as soluções da equação característica

$\det(A-\lambda I)=0~,$

onde $I$ é a matriz de identidade da mesmo tamanho que $A$ e $\lambda$ é um número (escalar) que resolve a equação (não existem mais que $n$ soluções, onde $n$ é o tamanho de $A$).

Uma matriz hermitiana é positiva definida se todos os seus autovalores forem positivos. O critério de Sylvester afirma que isso é equivalente ao fato dos determinantes das submatrizes

$A_{k}:={\begin{bmatrix}a_{1,1}&a_{1,2}&\dots &a_{1,k}\\a_{2,1}&a_{2,2}&\dots &a_{2,k}\\\vdots &\vdots &\ddots &\vdots \\a_{k,1}&a_{k,2}&\dots &a_{k,k}\end{bmatrix}}.$

serem positivos para todo $k$ entre $1$ and $n$.

O traço $\operatorname {tr} (A)$ é, por definição, a soma das $n$ entradas da diagonal de $A_{n\times n}$. Ele também é igual à soma dos $n$ autovalores de $A$.

Aplicações

Independência Linear

O determinante de uma matriz (com entradas reais ou complexas, por exemplo) é zero se e somente se os vetores de coluna (ou os vetores de linha) da matriz forem linearmente dependentes. Assim, determinantes podem ser usados para caracterizar vetores linearmente dependentes. Por exemplo, dados dois vetores linearmente independentes $v_{1},v_{2}$ em $\mathbb {R} ^{3}$, um terceiro vetor $v_{3}$ está no plano gerado pelos dois primeiros vetores se o determinante da matriz de ordem 3 que consiste nos três vetores for zero.

A mesma ideia também é usada na teoria das equações diferenciais: dadas $n$ funções $f_{1}(x),...,f_{n}(x)$ (supostamente $n-1$ vezes diferenciáveis), o Wronskiano é definido como

$W(f_{1},\ldots ,f_{n})(x)={\begin{vmatrix}f_{1}(x)&f_{2}(x)&\cdots &f_{n}(x)\\f_{1}'(x)&f_{2}'(x)&\cdots &f_{n}'(x)\\\vdots &\vdots &\ddots &\vdots \\f_{1}^{(n-1)}(x)&f_{2}^{(n-1)}(x)&\cdots &f_{n}^{(n-1)}(x)\end{vmatrix}}.$

Ele é diferente de zero (para algum $x$), em um intervalo especificado, se e somente se as funções fornecidas e todas as suas derivadas até a ordem $n-1$ forem linearmente independentes. Se for demonstrado que o Wronskiano é zero para todo ponto de um intervalo, no caso de funções analíticas, isso implica que as funções fornecidas são linearmente dependentes.

Orientação de uma base

O determinante pode atribuir um número a cada sequência de $n$ vetores em $\mathbb {R} ^{n}$, usando a matriz quadrada cujas colunas (ou linhas) são os vetores. Por exemplo, uma matriz ortogonal com entradas em $\mathbb {R} ^{n}$ representa uma base ortonormal no espaço euclidiano. O determinante dessa matriz determina se a orientação da base é consistente ou oposta à orientação da base canônica. Se o determinante for +1, a base tem a mesma orientação. Se for -1, a base tem a orientação oposta.

De modo geral, se o determinante de uma matriz A é positivo, A representa uma transformação linear que preserva a orientação (se A é uma matriz ortogonal 2 × 2 ou 3 × 3, representa uma rotação), enquanto que se for negativo, A altera a orientação da base.

Volume e determinante jacobiano

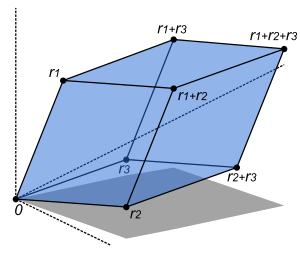
O valor absoluto do determinante de vetores reais é igual ao volume do paralelepípedo gerado por esses vetores. Como consequência, se $f:\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n}$ é o mapeamento linear representado pela matriz $A$ e $S$ é qualquer subconjunto mensurável de $\mathbb {R} ^{n}$, o volume de $f(S)$ é dado por $|\det(A)|$ vezes o volume de $S$. Em geral, se o mapeamento linear $f:\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}$ é representado pela matriz $A$, de ordem $m\times n$, então o volume $n$-dimensional de $f(S)$ é dado por:

$\operatorname {volume} (f(S))={\sqrt {\det \left(A^{\textsf {T}}A\right)}}\times \operatorname {volume} (S).$

Ao calcular o volume do tetraedro delimitado por quatro pontos, eles podem ser usados para identificar linhas de inclinação. O volume de qualquer tetraedro, dados seus vértices $a,b,c$ e $d$ é ${\frac {1}{6}}\,\left|\det(a-b,b-c,c-d)\right|$.

Para uma função diferenciável geral, grande parte do exposto acima se mantém ao se considerar a matriz jacobiana de $f$. Para

${\displaystyle f:\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n}}$

a matriz jacobiana é a matriz de ordem $n$ cujas entradas são dadas por

$D(f)=\left({\frac {\partial f_{i}}{\partial x_{j}}}\right)_{1\leq i,j\leq n}.$

Seu determinante, o jacobiano, aparece na versão de dimensão mais alta da integração por substituição: para funções convenientes $f$ e um subconjunto aberto $U$ de $\mathbb {R} ^{n}$ (o domínio de $f$), a integral sobre $f(U)$ de alguma outra função $g:\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}$ é dada por

$\int _{f(U)}\phi (\mathbf {v} )\,d\mathbf {v} =\int _{U}\phi (f(\mathbf {u} ))\left|\det(\operatorname {D} f)(\mathbf {u} )\right|\,d\mathbf {u} .$

O jacobiano também aparece no teorema da função inversa.

Determinante de Vandermonde (alternante)

O determinante de ordem 3 da matriz de Vandermonde é

$\left|{\begin{array}{ccc}1&1&1\\x_{1}&x_{2}&x_{3}\\x_{1}^{2}&x_{2}^{2}&x_{3}^{2}\end{array}}\right|=(x_{3}-x_{2})(x_{3}-x_{1})(x_{2}-x_{1}).$

Em geral, o determinante de Vandermonde de ordem $n$ é

$\left|{\begin{array}{ccccc}1&1&1&\cdots &1\\x_{1}&x_{2}&x_{3}&\cdots &x_{n}\\x_{1}^{2}&x_{2}^{2}&x_{3}^{2}&\cdots &x_{n}^{2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\x_{1}^{n-1}&x_{2}^{n-1}&x_{3}^{n-1}&\cdots &x_{n}^{n-1}\end{array}}\right|=\prod _{1\leq i<j\leq n}\left(x_{j}-x_{i}\right),$

onde o lado direito é o produto continuado de todas as diferenças que podem ser formadas a partir dos ${\frac {n(n-1)}{2}}$ pares de números retirados de $x_{1},x_{2},...,x_{n}$, com a ordem das diferenças encontradas na ordem invertida dos sufixos envolvidos.

Circulantes

Ver artigo principal: Matriz Circulante

Segunda ordem

$\left|{\begin{array}{cc}x_{1}&x_{2}\\x_{2}&x_{1}\end{array}}\right|=\left(x_{1}+x_{2}\right)\left(x_{1}-x_{2}\right).$

Terceira ordem

$\left|{\begin{array}{ccc}x_{1}&x_{2}&x_{3}\\x_{3}&x_{1}&x_{2}\\x_{2}&x_{3}&x_{1}\end{array}}\right|=\left(x_{1}+x_{2}+x_{3}\right)\left(x_{1}+\omega x_{2}+\omega ^{2}x_{3}\right)\left(x_{1}+\omega ^{2}x_{2}+\omega x_{3}\right),$

onde $\omega$ e $\omega ^{2}$ são as raízes cúbicas complexas de 1. Em geral, o determinante circulante de ordem $n$ é

$\left|{\begin{array}{ccccc}x_{1}&x_{2}&x_{3}&\cdots &x_{n}\\x_{n}&x_{1}&x_{2}&\cdots &x_{n-1}\\x_{n-1}&x_{n}&x_{1}&\cdots &x_{n-2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\x_{2}&x_{3}&x_{4}&\cdots &x_{1}\end{array}}\right|=\prod _{j=1}^{n}\left(x_{1}+x_{2}\omega _{j}+x_{3}\omega _{j}^{2}+\cdots +x_{n}\omega _{j}^{n-1}\right),$

onde $\omega _{j}^{n}$ é a n-ésima raiz de 1.

Ver também

• Matriz
• Matriz de Vandermonde
• Equação linear
• Transformação linear

Bibliografia

• Callioli, Carlos A.; Hygino H. Domingues; Roberto C. F. Costa (1990). Álgebra Linear e Aplicações 6 ed. São Paulo: Atual. ISBN 9788570562975