Economia matemática
| Parte da série sobre | ||
| Matemática | ||
|---|---|---|
|
||
A economia matemática é a aplicação de métodos matemáticos para representar teorias econômicas e analisar problemas propostos pela economia. Ela permite a formulação e derivação de relações chave em uma teoria com claridade, generalidade, rigor e simplicidade. Por convenção, os métodos se referem àqueles por trás da simples geometria, tais como cálculo diferencial e integral, equações diferenciais, álgebra matricial e programação matemática[1] e outros métodos computacionais.[2]
A matemática permite aos economistas formular proposições significativas e testáveis sobre muitos assuntos complexos e abrangentes que não poderiam ser adequadamente expressas informalmente. Além disso, a linguagem da matemática permite aos economistas fazer afirmações claras, específicas e positivas sobre assuntos controversos ou contenciosos que seriam impossíveis sem a matemática.[3] Grande parte da teoria econômica é atualmente apresentada em termos de modelos econômicos matemáticos, um conjunto de relações matemáticas estilizadas e simplificadas que clareiam suposições e implicações.[4]
Aplicações abrangentes incluem:
- Problemas de otimização para alcançar o equilíbrio, seja de famílias, de firmas, ou de decisores políticos;
- Análise estática (ou de equilíbrio) na qual a unidade econômica (tal como uma família) ou sistema econômico (tal como um mercado ou a economia) é modelado como imobilizado, sem mudanças;
- estática comparativa de uma mudança de um equilíbrio para outro induzido por uma mudança em um ou mais fatores;
- Análise dinâmica, rastreando mudanças em um sistema econômico ao longo do tempo, por exemplo, pelo crescimento econômico.[1][5][6]
A modelagem econômica formal começou no século XIX com o uso de cálculo diferencial para representar e explicar o comportamento econômico, tais como a maximização da utilidade, uma aplicação da otimização matemática. A economia tornou-se mais matemática como uma disciplina durante a primeira metade do século XX, mas a introdução de técnicas novas e generalizadas no período por volta da Segunda Guerra Mundial, como na teoria dos jogos, expandiria ainda mais o uso de formulações matemáticas na economia.[7][6]
Essa rápida sistematização da economia assustou os críticos da disciplina bem como de alguns economistas notórios. John Maynard Keynes, Robert Heilbroner, Friedrich Hayek e outros criticaram o uso indiscriminado de modelos matemáticos do comportamento humano, argumentando que algumas escolhas humanas não são traduzíveis para a matemática.
História[editar | editar código-fonte]
O uso da matemática a serviço da análise social e econômica data de antes do século XVII. Principalmente nas universidades alemãs, um estilo de instrução emergiu, que lidava especificamente com a apresentação detalhada de dados como relacionados à administração pública. Gottfried Achenwall enveredou nesse estilo, cunhando o termo estatística. Ao mesmo tempo, um pequeno grupo de professores na Inglaterra estabeleceu um método de "raciocínio por números quanto às coisas relativas ao governo" e chamou esta prática de Political Arithmetick.[8] Sir William Petty escreveu sobre assuntos que mais tarde iriam receber atenção dos economistas, tais como taxação, velocidade da moeda e renda nacional, mas apesar de sua análise ser numérica, ele rejeitou a metodologia matemática abstrata. O uso de Petty de dados numéricos detalhados (junto com John Graunt) influenciaria estatísticos e economistas por algum tempo, apesar das obras de Petty terem sido amplamente ignoradas por acadêmicos ingleses.[9]
A matematização da economia começou de fato no século XIX. A maior parte da análise econômica da época era o que mais tarde se chamaria economia clássica. Os assuntos eram discutidos usando meios algébricos, mas o cálculo não era usado. Até a publicação de The Isolated State, de Johann Heinrich von Thünen, em 1826, os economistas não desenvolveram modelos explícitos e abstratos para o comportamento a fim de aplicar ferramentas da matemática. O modelo de Thünen para o uso da terra representa o primeiro exemplo da análise marginal.[10] A obra de Thünen foi em sua maior parte teórica, mas ele também buscou dados empíricos a fim de tentar dar suporte a suas generalizações. Em comparação com seus contemporâneos, Thünen construiu modelos e ferramentas econômicos, ao invés de apenas aplicar ferramentas já existentes a problemas novos.[11]
Enquanto isso, um novo grupo de estudiosos buscaram aprender os métodos matemáticos das ciências físicas, defendendo e aplicando esses métodos a seus campos.[12] Nesse grupo incluía-se W.S. Jevons, que apresentou um artigo sobre "teoria matemática geral da economia política" em 1862, fornecendo um resumo para uso da teoria da utilidade marginal na economia política.[13] Em 1871, ele publicou Os Princípios da Economia Política, declarando que o assunto, como ciência, "deve ser matematicamente simples, pois ela elida com quantidades". Jevons esperava que dados estatísticos de preços e quantidades permitiriam que seu campo se tornasse uma ciência exata.[14] Outros economistas o precederam e seguiram na expansão das representações matemáticas de problemas econômicos.
Os marginalistas e as raízes da economia neoclássica[editar | editar código-fonte]
Augustin Cournot e Léon Walras construíram as ferramentas da disciplina axiomaticamente ao redor da utilidade, argumentando que os indivíduos buscam maximizar suas utilidades pelas escolhas de uma forma que poderia ser descrita matematicamente.[15] Na época, pensava-se que a utilidade era quantificável. Cournot, Walras e Francis Ysidro Edgeworth são considerados os precursores da moderna economia matemática.[16]
Augustin Cournot[editar | editar código-fonte]
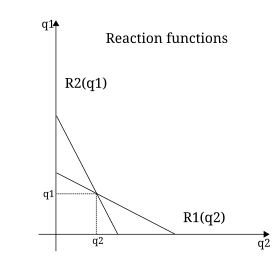
Cournot, um professor de matemática, desenvolveu um tratamento matemático em 1838 para o duopólio - uma condição de mercado definida pela competição entre dois vendedores.[16] Esse tratamento de competição, publicado pela primeira vez em Researches into the Mathematical Principles of Wealth,[17] é chamado de duopólio de Cournot. Assume-se que ambos os vendedores possuem acesso igual ao mercado e que podem produzir seus bens sem custos. Além disso, assume-se que ambos os bens são homogêneos. Cada vendedor variaria sua produção baseado na produção do outro e o preço de mercado seria determinado pela quantidade total ofertada. O lucro de cada firma seria determinado pela multiplicação de sua produção pelo preço de mercado unitário. Diferenciando a função de lucro quanto à quantidade ofertada por cada firma levaria a um sistema de equações lineares, com uma solução simultânea que daria a quantidade, preço e lucros de equilíbrio.[18] As contribuições de Cournot para a matematização da economia seriam negligenciadas por décadas, mas posteriormente influenciariam muitos dos marginalistas.[18][19] Os modelos de Cournot de duopólio e oligopólio também representam uma das primeiras formulações de jogo não-cooperativo. Atualmente, a solução pode ser considerada um equilíbrio de Nash, apesar de ter a obra de Cournot precedido a moderna teoria dos jogos em mais de 100 anos.[20]
Léon Walras[editar | editar código-fonte]
Enquanto Cournot forneceu uma solução para o que mais tarde seria chamado de equilíbrio parcial, Léon Walras tentou formalizar a discussão da economia como um todo através da teoria do equilíbrio geral. O comportamento de cada ator econômico seria considerado tanto do lado da produção quanto do lado do consumo. Walras originalmente apresentou quatro modelos separados de troca, cada um recursivamente incluído no próximo. A solução do sistema de equações resultante (tanto linear quanto não-linear) é o equilíbrio geral.[21] Na época, nenhuma solução geral poderia ser expressa para um sistema de muitas equações, mas as tentativas de Walras produziram dois resultados famosos na economia. O primeiro é a lei de Walras e o segundo é o princípio de tentativa e erro. O método de Walras era considerado altamente matemático para a época e Edgeworth comentou longamente sobre este fato em sua resenha de Éléments d'économie politique pure (Elementos da Economia Política Pura).[22]
A lei de Walras foi introduzida como uma resposta teórica ao problema de determinação das soluções no equilíbrio geral. Sua notação é diferente da notação moderna mas pode ser construída usando uma notação resumida mais moderna. Walras supunha que no equilíbrio, todo o dinheiro seria gasto com todos os bens: cada bem seria vendido a preço de mercado para aquele bem, e todo comprador gastaria até sua última moeda em uma cesta de bens. A partir dessa suposição, Walras poderia, então, mostrar que se existissem n mercados e n-1 mercados limpos (que alcançaram condições de equilíbrio), o n-ésimo mercado também estaria em equilíbrio. Isto é mais fácil de se visualizar com dois mercados (considerados em muitos textos como um mercado de bens e um merado de dinheiro). Se um dos dois mercados alcançasse um estado de equilíbrio, nenhum bem adicional (ou inversamente, dinheiro) poderia entrar ou sair do segundo mercado, assim ele deveria estar também em um estado de equilíbrio. Walras usou essa afirmação para provar a existência de soluções de equilíbrio geral mas atualmente é muito usada para ilustrar o equilíbrio em mercados de dinheiro a nível de graduação.[23]
Tâtonnement (em francês, para apalpando) foi usada como a expressão prática do equilíbrio geral walrasiano. Walras abstraiu o mercado como um leilão de bens onde o leiloeiro gritaria os preços e os participantes do mercado esperariam até que cada um deles pudesse satisfazer seus preços de reserva pessoais para a quantidade desejada (lembrando que se trata de um leilão com todos os bens, assim todos têm um preço de reserva para sua cesta desejada de bens).[24]
Apenas quando todos os compradores estivessem satisfeitos com o preço de mercado dado é que as transações ocorreriam. O mercado entraria em equilíbrio exatamente no preço - nenhum excedente ou escassez existiria. A palavra tâtonnement é usada para descrever as direções que o mercado toma apalpando para o equilíbrio, definindo preços mais altos ou baixos em diferentes bens até que um preço seja acordado para todos os bens. Apesar de o processo parecer dinâmico, Walras apresentou apenas um modelo estático, com nenhuma transação ocorrendo até que todos os mercados estivessem em equilíbrio. Na prática, muitos poucos mercados operam dessa maneira.[25]
Francis Ysidro Edgeworth[editar | editar código-fonte]
Edgeworth introduziu elementos matemáticos à economia explicitamente em Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences, publicado em 1881.[26] Ele adotou o cálculo da felicidade de Jeremy Bentham para o comportamento econômico, permitindo o resultado de cada de cisão ser convertido em uma mudança na utilidade.[27] Usando essa suposição, Edgeworth construiu um modelo de trocas com três suposições: os indivíduos são egoístas, os indivíduos agem para maximizar sua utilidade, e os indivíduos são "livres para recontratar com outros independentemente de qualquer terceira parte".[28]
Dados dois indivíduos, o conjunto de soluções em que ambos os indivíduos podem maximizar sua utilidade é descrito como a curva de contrato, no que hoje é conhecida como a caixa de Edgeworth. Tecnicamente, a construção da solução de duas pessoas do problema de Edgeworth não foi desenvolvida graficamente até 1924 por Arthur Lyon Bowley.[29] A curva de contrato da caixa de Edgeworth (ou, de modo mais geral, qualquer conjunto de soluções para o problema de Edgeworth com muitos atores) é chamada de núcleo de uma economia.[30]
Edgeworth dedicou um esforço considerável insistindo que as provas matemáticas era apropriadas para todas as escolas de pensamento na economia. Enquanto à frente do The Economic Journal, ele publicou alguns artigos criticando o rigor matemático dos pesquisadores rivais, incluindo Edwin Robert Anderson Seligman, um cético da economia matemática.[31] Os artigos focavam-se na incidência de impostos e nas respostas dos produtores. Edgeworth percebeu que um monopólio que produz um bem que tem ações coordenadas da oferta mas sem cooperação na demanda (tais como a primera classe e a econômica em um avião, se o avião voa, ambos conjuntos de assentos voam ao mesmo tempo) pode até diminuir o preço visto pelo consumidor para um ou dois produtos se o imposto fosse aplicado. De senso comum e mais tradicional, a análise numérica parecia indicar que isto era um absurdo. Seligman insistiam que os resultados que Edgeworth alcançou eram um truque de sua formulação matemática. Ele sugeriu que a suposição de uma função contínua de demanda e uma mudança infinitesimal nos impostos resultavam nas suposições paradoxicais. Harold Hotelling mais tarde mostrou que Edgeworth estava correto e que o mesmo resultado (uma "diminuição de preço como resultado do imposto") poderia ocorrer com uma função descontínua de demanda e grandes mudanças da na taxa de impostos.[32]
Economia matemática moderna[editar | editar código-fonte]
No final da década de 1930, os economistas viam um amplo uso de uma variedade de ferramentas matemáticas, incluindo conjuntos convexos e teoria dos grafos. Os matemáticos começaram a discutir problemas econômicos como um meio de avançar o nível da matemática pura da mesma forma que as soluções para os problemas na física levaram ao avanço na matemática de base.[33]
Cálculo diferencial[editar | editar código-fonte]
Vilfredo Pareto analisou a microeconomia ao tratar decisões de atores econômicos como tentativas de mudar uma dada alocação de bens para outra, uma alocação mais preferida. Conjuntos de alocações poderiam então ser tratadas como eficientes de Pareto (ótimo de Pareto é um termo equivalente) quando nenhuma troca poderia ocorrer entre atores que poderiam deixar ao menos um indivíduo em melhor situação sem deixar outro indivíduo pior.[34] A prova de Pareto é frequentemente confundida com o equilíbrio walrasiano ou informalmente atribuída a hipótese de mão invisível de Adam Smith.[35] Ao contrário, a afirmação de Pareto foi a primeira afirmação formal do que seria conhecido como o primeiro teorema fundamental da economia do bem estar.[36] Faltavam a esses modelos as desigualdades da geração seguinte da economia matemática.
No histórico tratado Foundations of Economic Analysis (1947), Paul Samuelson identificou um paradigma e estrutura matemática comuns em diferentes campos do assunto, com base nos trabalhos anteriores de Alfred Marshall. Foundations aproveitou conceitos matemáticos da física e aplicou-os a problemas econômicos. Essa visão ampla (por exemplo, comparando o Princípio de Le Châtelier com o leilão walrasiano) originou a premissa fundamental da economia matemática: sistemas de atores econômicos podem ser modelados e seu comportamento pode ser descrito assim como qualquer outro sistema. Esta extensão continuou a obra dos marginalistas no século anterior e a estendeu significativamente. Samuelson abordou o problema de aplicar a maximização da utilidade individual em grupos agregados com a estática comparativa, que compara dois diferentes estados de equilíbrio após uma mudança exógena em uma variável. Este e outros métodos no livro forneceram os fundamentos para a economia matemática do século XX.[6][37]
Modelos lineares[editar | editar código-fonte]
Modelos restritos de equilíbrio geral foram formulados por John von Neumann em 1938: Ao contrários das versões anteriores, os modelos de von Neumann tinham restrições de desigualdade. Para seu modelo de uma economia em expansão, von Neumann provou a existência e a unicidade de um equilíbrio usando sua generalização do teorema do ponto fixo de Brouwer. O modelo de uma economia em expansão de von Neumann considerava a o elemento A - λ B com matrizes não-negativas A e B. Von Neumann utilizou os vetores de probabilidade p e q e um número positivo λ que resolveria a equação de complementaridade
- pT (A - λ B) q = 0,
junto com dois sistemas de desigualdade que expressam a eficiência econômica. Neste modelo, o vetor de probabilidade (matriz transposta) p representa os preços dos bens enquanto o vetor de probabilidade q representa a "intensidade" com a qual o processo de produção ocorreria. A solução única λ representa a taxa de crescimento da economia, que iguala a taxa de juros. Provar a existência de uma taxa de crescimento positiva e as taxas de juros iguais foram avanços notáveis, até mesmo para von Neumann.[38][39][40] Osresultados de von Neumann foram vistos como um caso especial de programação linear, no qual o modelo de von Neumann usa apenas matrizes não-negativas.[41] O estudo do modelo de von Neumann de uma economia em expansão continua a interessar economistas matemáticos com interesse com economia computacional.[42][43][44]
Economia input-output[editar | editar código-fonte]
Em 1936, o economista russo Wassily Leontief construiu seu modelo de análise input-output a partir das tabelas de 'balanço de materiais' construídas por economistas soviéticos, que haviam se inspirado nas obras de economistas austríacos e fisiocratas. Com seu modelo, que descrevia um sistema de processos de produção e demanda, Leontief descrevia como as mudanças na demanda em um setor econômico influenciaria a produção em outro setor.[45] Na prática, Leontief estimou os coeficientes de seus modelos simples, a fim de abordar questões de interesse econômico. Na economia da produção, as "tecnologias de Leontief" produzem resultados usando proporções constantes de insumos (input), independentemente de seus preços, reduzindo o valor dos modelos de Leontief para a compreensão das economias, mas permitindo que seus parâmetros fossem estimados com relativa facilidade. Em contraste, o modelo de von Neumann de uma economia em expansão permite a escola de técnicas, mas os coeficientes precisam ser estimados para cada tecnologia.[46][47]
Otimização matemática[editar | editar código-fonte]
Problemas de otimização aparecem na economia moderna, muitos com restrições econômicas ou técnicas explícitas. Propriedades de otimalidade para um sistema de mercado pode ser traduzida em termos matemáticos, assim como para o modelo Arrow-Debreu de equilíbrio geral.[48] Mais concretamente, muitos problemas são passíveis de solução analítica (fórmulas). Muitos outros podem ser suficientemente complexos para exigir métodos numéricos de solução, auxiliado por softwares.[49]
A programação linear e não-linear enriqueceu profundamente a microeconomia, que anteriormente considerava apenas restrições de igualdade.[50] Muitos dos economistas matemáticos que receberam Prêmios Nobel de Economia conduziram pesquisas notáveis usando a programação linear: Leonid Kantorovich, Leonid Hurwicz, Tjalling Koopmans, Kenneth J. Arrow, e Robert Dorfman, Paul Samuelson, e Robert Solow.[51] Tanto Kantorovich quanto Koopmans reconheciam que George Dantzig merecia compartilhar os seus Prêmios Nobel pela programação linear. Economistas que conduziram pesquisas em programação não linear também ganharam Prêmios Nobel, nomeadamente Ragnar Anton Kittil Frisch, além de Kantorovich, Hurwicz, Koopmans, Arrow, e Samuelson.
Otimização linear[editar | editar código-fonte]
A programação linear foi desenvolvida para auxiliar a alocação de recursos nas firmas e em indústrias durante a década de 1930 na Rússia e durante a década de 1940 nos Estados Unidos. Durante o bloqueio de Berlim (1948), a programação linear foi usada para planejar o transporte de suprimentos a fim de prevenir que Berlim morresse de fome depois do bloqueio soviético.[52][53]
Programação não linear[editar | editar código-fonte]
Extensões da otimização não-linear com restrições de desigualdade surgiram em 1951 por Albert W. Tucker e Harold Kuhn, que consideraram o problema de otimização não-linear:
onde é a função a ser minimizada, são as funções das restrições de desigualdade e são as funções de restrições de igualdade, e e são o número de desigualdades e restrições de igualdade, respectivamente. Ao permitir restrições de desigualdade, a abordagem de Kuhn-Tucker generalizou o método clássico de multiplicadores de Lagrange, que (até então) permitia apenas restrições de igualdade.[54] A abordagem de Kuhn-Tucker inspirou mais pesquisas sobre a dualidade lagrangeana, incluindo o tratamento das restrições de desigualdade.[55][56][57][58] A teoria da dualidade da programação não-linear é particularmente satisfatória quando aplicada a problemas de minimização convexa, que se aproveita da teoria da dualidade convexo-analítica de Fenchel e Rockafellar. Essa dualidade convexa é particularmente forte para funções convexas poliédricas, tais como aquelas que aparecem na programação linear. A dualidade lagrangeana e a análise convexa são usadas diariamente em operações de investigação, programação de usinas nucleares, o planejamento de produção de fábricas e na definição de rotas de companhias aéreas.[58][59]
Teoria dos jogos[editar | editar código-fonte]
Trabalhando com Oskar Morgenstern no livro de theory of games, von Neumann declarou que a teoria econômica necessitava usar métodos analíticos funcionais, especialmente conjuntos convexos e o teorema do ponto fixo topológico, ao invés do tradicional cálculo diferencial, porque o operador-máximo não preservava diferentes funções. Continuando com o trabalho de von Neumann na teoria do jogo cooperativo, os teoristas dos jogos Lloyd S. Shapley, Martin Shubik, Hervé Moulin, Nimrod Megiddo e Bezalel Peleg influenciaram a pesquisa econômica. Por exemplo, pesquisas sobre preços justos em jogos cooperativos e valores justos para jogos de votação levaram a regras diferentes para votação nas legislaturas e na contabilidade de custos em projetos de obras públicas: um exemplo é o uso da teoria do jogo cooperativo no projeto de um sistema de distribuição de água no sul da Suécia, e a instalação de linhas telefônicas dedicadas nos Estados Unidos.
Seguindo o programa de von Neumann, John Nash usou a teoria do ponto fixo para provar que seus jogos não-cooperativos e seus problemas de barganha tinham equilíbrio. Por décadas, a teoria do jogo não-cooperativo foi adotada por um grande número de microeconomistas, cuja obra iluminou problemas de organização industrial. Em 1994, Nash, John Harsanyi, e Reinhard Selten receberam o Prémio de Ciências Económicas em Memória de Alfred Nobel pelas suas obras sobre jogos não-cooperativos. Harsanyi e Selten foram premiados por sua obra sobre jogos repetidos.
Economia computacional baseada no agente[editar | editar código-fonte]
A economia computacional baseada no agente é uma abordagem recente que se aproveita da teoria dos jogos e avanços nas técnicas computacionais e analíticas para modelar sistemas econômicos como resultados de "agentes intencionais que interagem no espaço e no tempo e cujas interações criam padrões emergentes."[60]
Análise funcional[editar | editar código-fonte]
Seguindo o programa de von Neumann, Kenneth Arrow e Gérard Debreu formularam modelos abstratos de equilíbrio econômico usando conjuntos convexos e a teoria do ponto fixo. Introduziram o modelo Arrow-Debreu em 1954 e provaram a existência (mas não unicidade) de um equilíbrio e também que todo equilíbrio walrasiano é eficiente de Pareto. Em geral, os equilíbrios não precisam ser únicos.[61] Em seus modelos, o espaço vetorial ("primal") representa quantidades enquanto o espaço vetorial "dual" representa preços.[62]
Na Rússia, o matemático Leonid Kantorovich desenvolveu modelos econômicos em espaços vetoriais parcialmente ordenados, que enfatizavam a dualidade entre quantidades e preços.[63] Oprimido pelo comunismo, Kantorovich renomeou os preços como "valores objetivamente determinados", que era abreviados em russo como "o. o. o.", em alusão à dificuldade de discutir preços na União Soviética.[62][64][65]
Mesmo em finitas dimensões, os conceitos de análise funcional iluminaram a teoria econômica, particularmente na clarificação do papel dos preços como vetores normais de um hiperplano dando suporte a um conjunto convexo, representando possibilidades de produção ou consumo. No entanto, problemas de descrição da otimização com o passar do tempo ou sob incerteza exigem o uso de espaços de função com dimensões infinitas, porque os agentes escolhem entre funções ou processos estocásticos.[62][66][67][68]
Cálculo de variações e controle ótimo[editar | editar código-fonte]
O problema de encontrar funções ótimas é estudado no cálculo de variações e na teoria do controle ótimo. Antes da Segunda Guerra Mundial, Frank Ramsey e Harold Hotelling usaram o cálculo de variações para econtrar soluções ótimas para problemas econômicos dinâmicos.
A teoria do controle ótimo começou a ser usada para resolver problemas dinâmicos na economia, especialmente os modelos de crescimento econômico, logo após a obra de Richard Bellman sobre programação dinâmica e após a publicação da tradução inglesa do livro de Pontryagin et al.[69] Aplicações da teoria do controle ótimo incluem aquelas em crescimento econômico, finanças, inventórios e produção, por exemplo.[70]
Renascença diferencial[editar | editar código-fonte]
Como discutido abaixo, seguindo as inovações de John von Neumann na economia, e particularmente após sua introdução de análise funcional e topologia na teoria econômica, a economia matemática avançada teve poucas aplicações de cálculo diferencial. Em particular, os teoristas do equilíbrio geral usavam a topologia geral, geometria convexa e teoria da otimização mais do que o cálculo diferencial, pois a abordagem do cálculo diferencial falhou em estabelecer a existência de um equilíbrio.
Entretanto, o declínio do cálculo diferencial não deveria ser exagerado, pois ele sempre foi usado na pós-graduação e em aplicações. Além disso, o cálculo diferencial havia retornado aos mais altos níveis da economia matemática e teoria do equilíbrio geral, como praticado pelo "GET-set" (o nome jocoso dado por Jacques H. Drèze). Nas décadas de 1960 e 1970, no entato, Gérard Debreu e Stephen Smale lideraram um renascimento da utilização do cálculo diferencial na economia matemática. Em particular, eles foram capazes de provar a existência de um equilíbrio geral, sendo que os economistas anteriores haviam falhado, usando suas novas ferramentas: Espaço de Baire da topologia geral e o lema de Sard da topologia diferencial. Outros economistas associados ao uso da análise diferencial incluem Egbert Dierker, Andreu Mas-Colell, e Yves Balasko.[71][72] Esses avanços mudaram a narrativa tradicional da história da economia matemática, seguindo von Neumann, que celebrou o abandono do cálculo diferencial.
A matematização da economia[editar | editar código-fonte]

Ao longo do século XX, artigos nos principais jornais[74] de economia eram escritos quase que exclusivamente por economistas da academia. Como um resultado, a maior parte do material transmitido nesses jornais era relacionado à teoria econômica, e "a própria teoria econômica estava continuamente sendo mais abstrata e matemática".[75] Uma avaliação subjetiva das técnicas matemáticas[76] empregadas nesses jornais mostrou uma diminuição nos artigos que não usavam nem representações geométricas nem notação matemática de 95% em 1892 para 5,3% em 1990.[77] Uma pesquisa de 2007 em dez dos mais conceituados jornais econômicos descobriu que apenas 5,8% dos artigos publicados em 2003 e 2004 não usavam a análise estatística de dados e expressões matemáticas que eram indexadas a números na margem da página.[78]
Econometria[editar | editar código-fonte]
Entre as guerras mundiais, os avanços na estatística matemática e um grupo de economistas matematicamente treinados levaram ao surgimento da econometria, que era o nome proposto para a disciplina da economia avançada que usava matemática e estatística. Na economia, a "econometria" normalmente foi usada para métodos estatísticos na economia, ao invés da economia matemática. A econometria estatística apresenta a aplicação da regressão linear e análise de séries de tempo para dados econômicos.
Ragnar Frisch cunhou a palavra "econometria" e ajudou a fundar tanto a Econometric Society em 1930, quanto o jornal Econometrica em 1933.[79][80] Um estudante de Frisch, Trygve Haavelmo publicou The Probability Approach in Econometrics em 1944, onde ele asseverou que a análise estátistica precisa poderia ser usada como uma ferramenta para validar teorias matemáticas sobre atores econômicos com dados de fontes complexas.[81] Essa ligação da análise estatística de sistemas com a teoria econômica foi também promulgada pela Comissão Cowles (hoje a Cowles Foundation) nas décadas de 1930 e 1940.[82]
Primeiras obras na econometria[editar | editar código-fonte]
As raízes da econometria moderna podem ser traçadas até o economista norte-americano Henry L. Moore. Moore estudou a produtividade agrícola e tentou encaixar valores variáveis de produtividade para lotes de milhos e outras plantações em uma curva usando diferentes valores de elasticidade. Moore fez alguns erros em sua obra, algumas de sua escolha de modelos e algumas das limitações em seu uso da matemática. A precisão dos modelos de Moore também foi limitada pelos poucos dados da contabilidade nacional dos Estados Unidos na época. Apesar de seus primeiros modelos de produção serem estáticos, em 1925 ele publicou um modelo de "equilíbrio móvel" dinâmico projetado para explicar ciclos econômicos - essa variação periódica de hipercorreção nas curvas de oferta e demanda é agora conhecida como o modelo cobweb (modelo teia de aranha). Uma derivação mais formal desse modelo foi feita mais tarde por Nicholas Kaldor, que é creditado por sua popularização.[83]
Aplicação[editar | editar código-fonte]

A maior parte da economia clássica pode ser apresentada em termos geométricos simples ou notação matemática elementar. A economia matemática, no entanto, convencionalmente faz uso do cálculo e álgebra matricial na análise econômica a fim de fazer afirmações poderosas que seriam mais difíceis sem tais ferramentas matemáticas. Essas ferramentas são pré-requisitos para o estudo formal, não apenas na economia matemática mas na teoria econômica contemporânea em geral. Os problemas econômicos normalmente envolvem tantas variáveis que a matemática é a única forma prática de atacá-los e resolvê-los. Alfred Marshall argumentou que todo problema econômico que pode ser quantificado, analiticamente expresso e resolvido, deveria ser tratado por meios do trabalho matemático.[85]
A economia se tornou cada vez mais dependente de métodos matemáticos e as ferramentas que ela emprega se tornaram mais sofisticadas. Como um resultado, a matemática tornou-se consideravelmente mais importante aos profissionais em economia e finanças. Programas de gradução em economia e finanças exigem uma forte preparação de pós-graduação em matemática para admissão e, por esta razão, atraem um crescente número de matemáticos. Os matemáticos aplicados usam princípios matemáticos para problemas práticos, tais como a análise econômica e outros assuntos relacionados à economia, sendo que muitos problemas econômicos são definidos como integrados no escopo da matemática aplicada.[15]
Essa integração resulta da formulação de problemas econômicos como modelos estilizados com suposições limpas e previsões falseáveis. Essa modelagem pode ser informal ou prosaica, como foi em A Riqueza das Nações de Adam Smith, ou pode ser formal, rigorosa e matemática.
De um modo geral, modelos econômicos formais poderiam ser classificados como estocástico ou determinístico e como discreto ou contínuo. Em nível prático, a modelagem quantitativa é aplicada a muitas áreas da economia e algumas metodologias haviam evoluído mais ou menos independentemente das outras.[86]
- Modelos estocásticos são formulados usando processos estocásticos. Eles modelam valores economicamente observáveis com o passar do tempo. A maior parte da econometria é baseada na estatística para formular e testar hipóteses sobre esses processos ou estimar parâmetros para eles. Entre as Grandes Guerras, Herman Wold desenvolveu uma representação de processos estocásticos estacionários em termos de modelos autoregressivos e uma tendência determinista. Wold e Jan Tinbergen aplicaram a análise de séries temporais a dados econômicos. Pesquisas contemporâneas sobre estatística de séries temporais consideram formulações adicionais de processos estacionários, tais como modelos de média móvel autorregressiva (ARMA). Modelos mais gerais incluem os de heterocedasticidade condicional autorregresiva (ARCH) e ARCH generalizados (GARCH).
- Os modelos matemáticos não-estocásticos podem ser puramente qualitativos (por exemplo, modelos envolvidos em algum aspecto da teoria da escolha social) ou quantitativos (envolvendo racionalização ou variáveis financeiras, por exemplo com coordenadas hiperbólicas e/ou formas específicas de relações funcionais entre variáveis). Em alguns casos, as previsões econômicas de um modelo meramente indicam a direção do movimento das variáveis econômicas, e, portanto, as relações funcionais são usadas somente em um sentido qualitativo: por exemplo, se o preço de um item aumenta, então a demanda por ele irá diminuir. Para tais modelos, os economistas normalmente usam gráficos de duas dimensões ao invés de funções.
- Modelos qualitativos algumas vezes são usados. Um exemplo é o planejamento de cenário qualitativo, no qual eventos futuros possíveis são desconsiderados. Outro exemplo é a análise não numérica de decisões em árvore. Os modelos qualitativos muitas vezes sofrem da falta de precisão.
Críticas e defesas[editar | editar código-fonte]
Adequação da matemática para economia qualitativa e complicada[editar | editar código-fonte]
Friedrich Hayek sustentava que o uso de técnicas formais projeta um rigor científico que não representa adequadamente as limitações informacionais encontradas pelos agentes econômicos reais.[87]
Previsões de teste da economia matemática[editar | editar código-fonte]
O filósofo Karl Popper discutiu o padrão científico da economia nas décadas de 1940 e 1950. Ele argumentou que a economia matemática sofria por ser tautológica. Em outras palavras, na medida em que a economia tornou-se uma teoria matemática, a economia matemática deixou de confiar na refutação empírica e passou a se voltar para provas e refutações matemáticas.[88] De acordo com Popper, suposições falseáveis podem ser testadas pela experiência e observação, enquanto as suposições infalsificáveis podem ser exploradas matematicamente pelas suas consequências e por sua consistência com outras suposições.[89]
Compartilhando as preocupações de Popper sobre suposições na economia em geral, e não apenas na economia matemática, Milton Friedman declarou que "todas as suposições são irrealistas". Friedman propôs julgar os modelos econômicos por seu poder preditivo ao invés da combinação entre suas suposições e a realidade.[90]
Economia matemática como uma forma de matemática pura[editar | editar código-fonte]
Considerando a economia matemática, John Maynard Keynes escreveu em A Teoria Geral:[91]
"É um grande erro dos métodos simbólicos pseudo-matemáticos formalizarem um sistema de análise econômica ... que eles expressamente assumem uma independência estrita entre os fatores envolvidos e perdem sua força de convicção e autoridade se essa hipótese não é permitida e que, no discurso comum, no qual não somos cegamente manipulados e sabemos todo o tempo o que estamos fazendo e o que as palavras significam, nós podemos manter "na parte de trás de nossas cabeças" as reservas e qualificações necessárias e as adaptações que teremos de fazer mais tarde, de um modo em que nós não podemos manter diferenciais parciais complicados "atrás" de algumas páginas de álgebra que, supõe-se, irão desaparecer. Uma grande proporção da economia matemática recente é meramente de misturas, tão imprecisas quanto as suposições iniciais nas quais elas se baseiam, e que fazem o autor perder a visão das complexidades e interdependências do mundo real em um labirinto de símbolos pretensiosos e inúteis".
Defesa da economia matemática[editar | editar código-fonte]
Em resposta a essas críticas, Paul Samuelson argumentou que a matemática é uma linguagem, repetindo a tese de Josiah Willard Gibbs. Na economia, a linguagem da matemática é algumas vezes necessária para representar problemas substantivos. Além disso, a economia matemática levou a avanços conceituais na economia.[92] Em particular, Samuelson deu o exemplo da microeconomia, escrevendo que "algumas pessoas são engenhosas o suficiente para entender suas partes mais complexas... sem recorrer à linguagem matemática, enquanto a maioria dos indivíduos comuns podem fazer isso facilmente com a ajuda da matemática."[93]
Alguns economistas dizem que a economia matemática merece um apoio assim como outras formas de matemática, particularmente seus irmãos na otimização e na estatística, e ainda mais na ciência da computação teórica. A economia matemática e outras ciências matemáticas possuem uma história na qual avanços teóricos têm contribuído regularmente para a reforma dos ramos mais aplicados da economia. Em particular, seguindo o programa de John von Neumann, a teoria dos jogos hoje fornece as bases para descrever grande parte da economia aplicada, da teoria da decisão estatística (como "jogos contra a natureza") e econometria à teoria do equilíbrio geral e organização industrial. No final do século XX, com o surgimento da internet, os economistas matemáticos e os especialistas em otimização e cientistas computacionais trabalharam em problemas de preços de serviços on-line - eles contribuíram usando matemática da teoria dos jogos cooperativos, otimização não-diferenciável e jogos combinatórios.
Robert Solow concluiu que a economia matemática era o núcleo da "infraestrutura" da economia contemporânea:
A economia não é mais uma conversação adequada para senhoras e senhores. Ela se tornou um assunto técnico. Assim como qualquer assunto técnico, ele atrai algumas pessoas que estão mais interessados na técnica do que propriamente no assunto. Isso é muito mau, mas pode ser inevitável. Em qualquer caso, não se engane: o núcleo técnico da economia é uma infraestrutura indispensável para a economia política. Por isso, se você consultar [uma referência na economia contemporânea] à procura do conhecimento sobre o mundo de hoje, você será levado à economia técnica, ou história, ou nada disso.[94]
Economistas matemáticos[editar | editar código-fonte]
Economistas matemáticos proeminentes incluem, mas não são limitados a, os seguintes (por século de nascimento).
Século XIX[editar | editar código-fonte]
- Enrico Barone
- Léon Walras
- Antoine Augustin Cournot
- Francis Ysidro Edgeworth
- Irving Fisher
- William Stanley Jevons
Século XX[editar | editar código-fonte]
Ver também[editar | editar código-fonte]
Referências
- ↑ a b Chiang, Alpha C.; and Kevin Wainwright (2005). Fundamental Methods of Mathematical Economics. [S.l.]: McGraw-Hill Irwin. pp. 3–4. ISBN 0-07-010910-9 TOC.
- ↑ Busca em The New Palgrave Dictionary of Economics Online, "mathematical economics" "computational" (em inglês).
- ↑ Varian, Hal (1997). "What Use Is Economic Theory?" in A. D'Autume and J. Cartelier, ed., Is Economics Becoming a Hard Science?, Edward Elgar. Pre-publication PDF (em inglês). Página acessada em 01/04/2008.
- ↑ As in Handbook of Mathematical Economics, links para primeira página do capítulo:
• Arrow, Kenneth J., and Michael D. Intriligator, ed., (1981), v. 1
• _____ (1982). v. 2
• _____ (1986). v. 3
• Hildenbrand, Werner, and Hugo Sonnenschein, ed. (1991). v. 4. - ↑ Chiang, Alpha C. (1992). Elements of Dynamic Optimization, Waveland. TOC Arquivado em 11 de dezembro de 2010, no Wayback Machine. & Amazon.com link to inside, first pp (em inglês).
- ↑ a b c Samuelson, Paul (1983). Foundations of Economic Analysis (em inglês). [S.l.]: Harvard University Press. ISBN 0-674-31301-1
- ↑ • Debreu, Gérard (2008). "mathematical economics," The New Palgrave Dictionary of Economics, 2nd Edition. Resumo.
• von Neumann, John, e Oskar Morgenstern (1944). Theory of Games and Economic Behavior. Princeton University Press (em inglês). - ↑ Schumpeter, J.A. (1954). Elizabeth B. Schumpeter, ed. History of Economic Analysis (em inglês). New York, NY: Oxford University Press. pp. 209–212. ISBN 9780043300862. OCLC 13498913
- ↑ Schumpeter (1954) p. 212-215.
- ↑ Schnieder, Erich (1934). «Johann Heinrich von Thünen». The Econometric Society. Econometrica (em inglês). 2 (1): 1–12. ISSN 0012-9682. JSTOR 1907947. OCLC 35705710. doi:10.2307/1907947
- ↑ Schumpeter (1954) p. 465-468.
- ↑ Philip Mirowski, 1991. "The When, the How and the Why of Mathematical Expression in the History of Economics Analysis," Journal of Economic Perspectives, 5(1) pp. 145-157[ligação inativa] (em inglês).
- ↑ Jevons, W.S. (1866). "Brief Account of a General Mathematical Theory of Political Economy," Journal of the Royal Statistical Society, XXIX (June) pp. 282-87. Read in Section F of the British Association, 1862. PDF[ligação inativa] (em inglês).
- ↑ Jevons, W. Stanley (1871). The Principles of Political Economy, pp. 4, 25. (em inglês). [S.l.: s.n.]
- ↑ a b Sheila C., Dow (21 de maio de 1999). «The Use of Mathematics in Economics». ESRC Public Understanding of Mathematics Seminar. Birmingham: Economic and Social Research Council. Consultado em 6 de julho de 2008
- ↑ a b Nicola, PierCarlo (2000). Mainstream Mathermatical Economics in the 20th Century (em inglês). [S.l.]: Springer. 4 páginas. ISBN 9783540670841. Consultado em 21 de agosto de 2008
- ↑ Augustin Cournot (1838, tr. 1897) Researches nto the Mathematical Principles of Wealth. Links para eescrição e capítulos (em inglês).
- ↑ a b Hotelling, Harold (1990). «Stability in Competition». In: Darnell, Adrian C. The Collected Economics Articles of Harold Hotelling (em inglês). [S.l.]: Springer. pp. 51, 52. ISBN 3540970118. OCLC 20217006. Consultado em 21 de agosto de 2008
- ↑ «Antoine Augustin Cournot, 1801-1877». The History of Economic Thought Website (em inglês). The New School for Social Research. Consultado em 21 de agosto de 2008. Arquivado do original em 31 de agosto de 2006
- ↑ Gibbons, Robert (1992). Game Theory for Applied Economists (em inglês). Princeton, New Jersey: Princeton University Press. pp. 14, 15. ISBN 0691003955
- ↑ Nicola, p. 9-12
- ↑ Edgeworth, Francis Ysidro (5 de setembro de 1889). «The Mathematical Theory of Political Economy: Review of Léon Walras, Éléments d'économie politique pure» (PDF). Nature (em inglês). 40 (1036): 434–436. ISSN 0028-0836. Consultado em 21 de agosto de 2008. Arquivado do original (PDF) em 11 de abril de 2003
- ↑ Nicholson, Walter; Snyder, Christopher, p. 350-353.
- ↑ Dixon, Robert. «Walras Law and Macroeconomics». Walras Law Guide (em inglês). Department of Economics, University of Melbourne. Consultado em 28 de setembro de 2008. Arquivado do original em 17 de abril de 2008
- ↑ Dixon, Robert. «A Formal Proof of Walras Law». Walras Law Guide (em inglês). Department of Economics, University of Melbourne. Consultado em 28 de setembro de 2008. Arquivado do original em 30 de abril de 2008
- ↑ Rima, Ingrid H. (1977). «Neoclassicism and Dissent 1890-1930». In: Weintraub, Sidney. Modern Economic Thought (em inglês). [S.l.]: University of Pennsylvania Press. pp. 10, 11. ISBN 0812277120
- ↑ Heilbroner, Robert L. (1999). The Worldly Philosophers (em inglês) Seventh ed. New York, NY: Simon and Schuster. pp. 172–175, 313. ISBN 9780684862149
- ↑ Edgeworth, Francis Ysidro (1961). Mathematical Psychics (em inglês). Londres: Kegan Paul [A. M. Kelley]. pp. 15–19
- ↑ Bowley, Arthur Lyon (1960). The Mathematical Groundwork of Economics: an Introductory Treatise (em inglês). Oxford: Clarendon Press [Kelly]
- ↑ Gillies, D. B. (1969). «Solutions to general non-zero-sum games». In: Tucker, A. W. & Luce, R. D. Contributions to the Theory of Games. Col: Annals of Mathematics (em inglês). 40. Princeton, New Jersey: Princeton University Press. pp. 47–85. ISBN 9780691079370
- ↑ Moss, Lawrence S. (2003). «The Seligman-Edgeworth Debate about the Analysis of Tax Incidence: The Advent of Mathematical Economics, 1892–1910». Duke University Press. History of Political Economy (em inglês). 35 (2): 207, 212, 219, 234–237. ISSN 0018-2702. doi:10.1215/00182702-35-2-205
- ↑ Hotelling, Harold (1990). «Note on Edgeworth's Taxation Phenomenon and Professor Garver's Additional Condition on Demand Functions». In: Darnell, Adrian C. The Collected Economics Articles of Harold Hotelling (em inglês). [S.l.]: Springer. pp. 94–122. ISBN 3540970118. OCLC 20217006. Consultado em 26 de agosto de 2008
- ↑ Herstein, I.N. (1953). «Some Mathematical Methods and Techniques in Economics». American Mathematical Society. Quarterly of Applied Mathematics. 11 (3): 249, 252, 260. ISSN 1552-4485
- ↑ Nicholson, Walter; Snyder, Christopher (2007). «General Equilibrium and Welfare». Intermediate Microeconomics and Its Applications (em inglês) 10th ed. [S.l.]: Thompson. pp. 364, 365. ISBN 0324319681
- ↑ Jolink, Albert (2006). «What Went Wrong with Walras?». In: Backhaus, Juergen G.; Maks, J.A. Hans. From Walras to Pareto. Col: The European Heritage in Economics and the Social Sciences. IV. [S.l.]: Springer. ISBN 978-0-387-33756-2. doi:10.1007/978-0-387-33757-9_6
• Blaug, Mark (2007). «The Fundamental Theorems of Modern Welfare Economics, Historically Contemplated». Duke University Press. History of Political Economy (em inglês). 39 (2): 186–188. ISSN 0018-2702. doi:10.1215/00182702-2007-001 - ↑ Blaug (2007), p. 185, 187
- ↑ Metzler, Lloyd (1948). «Review of Foundations of Economic Analysis». The American Economic Review, Vol. 38, No. 5. American Economic Review (em inglês). 38 (5): 905–910. ISSN 0002-8282. JSTOR 1811704
- ↑ Para esse problema ter uma única solução, é suficiente que as matrizes não-negativas A e B satisfaçam uma condição de irredutibilidade, generalizando aquele do teorema de Perron-Frobenius para matrizes não-negativas, que considera o problema de autovalor (simplificado)
- A - λ I q = 0,
- ↑ David Gale. The theory of linear economic models. McGraw-Hill, New York, 1960.
- ↑ Morgenstern, Oskar; Thompson, Gerald L. (1976). Mathematical theory of expanding and contracting economies. Col: Lexington Books (em inglês). Lexington, Massachusetts: D. C. Heath and Company. pp. xviii+277
- ↑ Alexander Schrijver, Theory of Linear and Integer Programming. John Wiley & sons, 1998, ISBN 0-471-98232-6.
- ↑
- Rockafellar, R. Tyrrell (1967). Monotone processes of convex and concave type. Col: Memoirs of the American Mathematical Society, 77 (em inglês). Providence, R.I.: American Mathematical Society. pp. i+74
- Rockafellar, R. T. (1974). «Convex algebra and duality in dynamic models of production». In: Josef Loz and Maria Loz. Mathematical models in economics (Proc. Sympos. and Conf. von Neumann Models, Warsaw, 1972) (em inglês). Amsterdam: North-Holland and Polish Adademy of Sciences (PAN). pp. 351–378
- Rockafellar, R. T.]] (1997). Convex analysis (em inglês). Princeton, NJ: Princeton University Press
- ↑ Kenneth Arrow, Paul Samuelson, John Harsanyi, Sidney Afriat, Gerald L. Thompson, and Nicholas Kaldor. (1989). Mohammed Dore, Sukhamoy Chakravarty, Richard Goodwin, ed. John Von Neumann and modern economics (em inglês). [S.l.]: Oxford:Clarendon. 261 páginas
- ↑ Chapter 9.1 "The von Neumann growth model" (pages 277–299): Yinyu Ye. Interior point algorithms: Theory and analysis. Wiley. 1997 (em inglês).
- ↑ Screpanti, Ernesto; Zamagni, Stefano (1993). An Outline of the History of Economic Thought (em inglês). New York, NY: Oxford University Press. pp. 288–290. ISBN 0198283709. OCLC 57281275
- ↑ David Gale. The theory of linear economic models. McGraw-Hill, New York, 1960 (em inglês).
- ↑ Morgenstern, Oskar; Thompson, Gerald L. (1976). Mathematical theory of expanding and contracting economies. Col: Lexington Books (em inglês). Lexington, Massachusetts: D. C. Heath and Company. pp. xviii+277
- ↑ • John Geanakoplos ((1987] 2008). "Arrow–Debreu model of general equilibrium," The New Palgrave Dictionary of Economics, 2nd Edition. Resumo (em inglês).
• Arrow, Kenneth J., and Gerard Debreu (1954). "Existence of an Equilibrium for a Competitive Economy," Econometrica 22(3), pp. 265-290 (em inglês). - ↑ Schmedders, Karl (2008). "numerical optimization methods in economics," The New Palgrave Dictionary of Economics, 2ª edição. Resumo (em inglês).
- ↑ Nicola, p. 133
- ↑ Dorfman, Robert, Paul A. Samuelson, and Robert M. Solow (1958). Linear Programming and Economic Analysis. McGraw–Hill. Chapter-preview links (em inglês).
- ↑ M. Padberg, Linear Optimization and Extensions, Second Edition, Springer-Verlag, 1999 (em inglês).
- ↑ Dantzig, George B. ([1987] 2008). "linear programming," The New Palgrave Dictionary of Economics, 2ª edição. Resumo (em inglês).
- ↑ Kuhn, H. W.; Tucker, A. W. (1951). «Nonlinear programming». Proceedings of 2nd Berkeley Symposium. Berkeley: University of California Press. pp. 481–492
- ↑ Bertsekas, Dimitri P. (1999). Nonlinear Programming 2ª ed. Cambridge, MA.: Athena Scientific. ISBN 1-886529-00-0
- ↑ • Lasdon, Leon S. (1970). Optimization theory for large systems. Col: Macmillan series in operations research (em inglês). New York: The Macmillan Company. pp. xi+523. MR 337317
• Lasdon, Leon S. (2002). Optimization theory for large systems (em inglês) reprint of the 1970 Macmillan ed. Mineola, New York: Dover Publications, Inc. pp. xiii+523. MR 1888251 - ↑ Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). «XII Abstract duality for practitioners». Convex analysis and minimization algorithms, Volume II: Advanced theory and bundle methods. Col: Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] (em inglês). 306. Berlin: Springer-Verlag. pp. 136–193 (and Bibliographical comments on pp. 334–335). ISBN 3-540-56852-2. MR 1295240
- ↑ a b Lemaréchal, Claude (2001). «Lagrangian relaxation». In: Michael Jünger and Denis Naddef. Computational combinatorial optimization: Papers from the Spring School held in Schloß Dagstuhl, May 15–19, 2000. Col: Lecture Notes in Computer Science (em inglês). 2241. Berlin: Springer-Verlag. pp. 112–156. ISBN 3-540-42877-1. MR 1900016. doi:10.1007/3-540-45586-8_4
- ↑ Intriligator, Michael D. (2008). "nonlinear programming," The New Palgrave Dictionary of Economics, 2nd Edition. TOC (em inglês).
- ↑
• Scott E. Page (2008). "agent-based models," The New Palgrave Dictionary of Economics, 2ª edição. Abstract.
• Leigh Tesfatsion (2006) "Agent-Based Computational Economics: A Constructive Approach to Economic Theory," pp. 831-880, in Leigh Tesfatsion and Kenneth Judd, ed., Handbook of Computational Economics, ch. 16, v. 2. Description Arquivado em 6 de março de 2012, no Wayback Machine. & and chapter-preview links (em inglês). - ↑ Weintraub, E. Roy (1977). «General Equilibrium Theory». In: Weintraub, Sidney. Modern Economic Thought (em inglês). [S.l.]: University of Pennsylvania Press. pp. 107–109. ISBN 0812277120
• Arrow, Kenneth J.; Debreu, Gérard (1954). «Existence of an equilibrium for a competitive economy». The Econometric Society. Econometrica (em inglês). 22 (3): 265–290. ISSN 0012-9682. JSTOR 1907353. doi:10.2307/1907353 - ↑ a b c Kantorovich, Leonid and Victor Polterovich. "Functional analysis." The New Palgrave Dictionary of Economics. 2ª Edição. Eds. Steven N. Durlauf and Lawrence E. Blume. Palgrave Macmillan, 2008. The New Palgrave Dictionary of Economics Online. Palgrave Macmillan. 15 de fevereiro de 2011 <http://www.dictionaryofeconomics.com/article?id=pde2008_F000236> doi:10.1057/9780230226203.0608 (em inglês).
- ↑ Kantorovich, L. V (1990). «"My journey in science (supposed report to the Moscow Mathematical Society)" [expanding Russian Math. Surveys 42 (1987), no. 2, pp. 233–270]». In: Lev J. Leifman. Functional analysis, optimization, and mathematical economics: A collection of papers dedicated to the memory of Leonid Vitalʹevich Kantorovich (em inglês). New York: The Clarendon Press, Oxford University Press. pp. 8–45. ISBN 0-19-505729-5. MR 898626
- ↑ Página 406: Polyak, B. T. (2002). «History of mathematical programming in the USSR: Analyzing the phenomenon (Chapter 3 The pioneer: L. V. Kantorovich, 1912–1986, pp. 405–407)». Mathematical Programming. Series B (em inglês). 91 (3). pp. 401–416. MR 1888984. doi:10.1007/s101070100258
- ↑ «Leonid Vitaliyevich Kantorovich — Prize Lecture ("Mathematics in economics: Achievements, difficulties, perspectives")». Nobelprize.org (em inglês). Consultado em 12 de dezembro de 2010
- ↑ Aliprantis, Charalambos D.; Brown, Donald J.; Burkinshaw, Owen (1990). Existence and optimality of competitive equilibria (em inglês). Berlin: Springer–Verlag. pp. xii+284. ISBN 3-540-52866-0. MR 1075992
- ↑ Rockafellar, R. Tyrrell. Conjugate duality and optimization. Lectures given at the Johns Hopkins University, Baltimore, Md., June, 1973. Conference Board of the Mathematical Sciences Regional Conference Series in Applied Mathematics, No. 16. Society for Industrial and Applied Mathematics, Philadelphia, Pa., 1974. vi+74 pp (em inglês).
- ↑ Lester G. Telser and Robert L. Graves Functional Analysis in Mathematical Economics: Optimization Over Infinite Horizons (em inglês) 1972. University of Chicago Press, 1972, ISBN 978-0-226-79190-6.
- ↑ Pontryagin, L. S.; Boltyanski, V. G., Gamkrelidze, R. V., Mischenko, E. F. (1962). The Mathematical Theory of Optimal Processes (em inglês). New York, NY: Wiley. ISBN 9782881240775
- ↑ Shell, K., ed. (1967). Essays on the Optimal Economic Growth (em inglês). Cambridge, MA: The MIT Press. ISBN 0262190362
• Arrow, K. J.; Kurz, M. (1970). Public Investment, the Rate of Return, and Optimal Fiscal Policy (em inglês). Baltimore, MD: The Johns Hopkins Press. ISBN 0801811244 Resumo Arquivado em 19 de julho de 2013, no Wayback Machine. (em inglês).
• Sethi, S. P.; Thompson, G. L. (2000). Optimal Control Theory: Applications to Management Science and Economics, Second Edition (em inglês). New York, NY: Springer. ISBN 0792386086 Scroll to chapter-preview links (em inglês). - ↑ Mas-Colell, Andreu (1985). The Theory of general economic equilibrium: A differentiable approach. Col: Econometric Society monographs, 9 (em inglês). [S.l.]: Cambridge UP. ISBN 0-521-26514-2. MR 1113262
- ↑ Yves Balasko. Foundations of the Theory of General Equilibrium (em inglês), 1988, ISBN 0-12-076975-1.
- ↑ Brockhaus, Oliver; Farkas, Michael; Ferraris, Andrew; Long, Douglas; Overhaus, Marcus (2000). Equity Derivatives and Market Risk Models (em inglês). [S.l.]: Risk Books. pp. 13–17. ISBN 9781899332878. Consultado em 17 de agosto de 2008
- ↑ Liner, Gaines H. (2002). «Core Journals in Economics». Oxford University Press. Economic Inquiry (em inglês). 40 (1). 140 páginas. doi:10.1093/ei/40.1.138
- ↑ Stigler, George J.; Stigler, Steven J.; Friedland, Claire (1995). «The Journals of Economics». The University of Chicago Press. The Journal of Political Economy (em inglês). 103 (2). 339 páginas. ISSN 0022-3808. JSTOR 2138643. doi:10.1086/261986
- ↑ Stigler et al. revisaram artigos nos principais jornais econômicos (como definido pelos autores, mas em geral significando jornais não-especiaistas) durante o século XX.Notou-se que os artigos de jornal que usavam representação geométrica ou notação matemática usavam esse nível de matemática como o "mais alto nível de técnica matemática". Os autores se referem a "técnicas verbais" como aquelas que transmitiam o assunto em questão sem notação de geometria, álgebra ou cálculo.
- ↑ Stigler et al., p. 342
- ↑ Sutter, Daniel and Rex Pjesky. "Where Would Adam Smith Publish Today?: The Near Absence of Math-free Research in Top Journals" (Maio de 2007). [1] (em inglês).
- ↑ Arrow, Kenneth J. (1960). «The Work of Ragnar Frisch, Econometrician». Blackwell Publishing. Econometrica (em inglês). 28 (2): 175–192. ISSN 0012-9682. JSTOR 1907716. doi:10.2307/1907716
- ↑ Bjerkholt, Olav (1995). «Ragnar Frisch, Editor of Econometrica 1933-1954». Blackwell Publishing. Econometrica (em inglês). 63 (4): 755–765. ISSN 0012-9682. JSTOR 1906940. doi:10.2307/2171799
- ↑ Lange, Oskar (1945). «The Scope and Method of Economics». The Review of Economic Studies Ltd. Review of Economic Studies (em inglês). 13 (1): 19–32. ISSN 0034-6527. JSTOR 2296113. doi:10.2307/2296113
- ↑ Aldrich, John (1989). «Autonomy». Oxford University Press. Oxford Economic Papers (em inglês). 41 (1, History and Methodology of Econometrics): 15–34. ISSN 0030-7653. JSTOR 2663180
- ↑ Epstein, Roy J. (1987). A History of Econometrics. Col: Contributions to Economic Analysis (em inglês). [S.l.]: North-Holland. pp. 13–19. ISBN 9780444702678. OCLC 230844893
- ↑ Colander, David C. (2004). «The Strange Persistence of the IS-LM Model». Duke University Press. History of Political Economy (em inglês). 36 (Annual Supplement): 305–322. ISSN 0018-2702. doi:10.1215/00182702-36-Suppl_1-305
- ↑ Brems, Hans (1975). «Marshall on Mathematics». University of Chicago Press. Journal of Law and Economics (em inglês). 18 (2): 583–585. ISSN 0022-2186. JSTOR 725308. doi:10.1086/466825
- ↑ Frigg, R.; Hartman, S. (27 de fevereiro de 2006). Edward N. Zalta, ed. Models in Science. Col: Stanford Encyclopedia of Philosophy (em inglês). Stanford, CA: The Metaphysics Research Lab. ISSN 1095-5054. Consultado em 16 de agosto de 2008
- ↑ Hayek, Friedrich (1945). «The Use of Knowledge in Society». American Economic Review (em inglês). 35 (4): 519–530. JSTOR 1809376
- ↑ Boland, L. A. (2007). «Seven Decades of Economic Methodology». In: I. C. Jarvie, K. Milford, D.W. Miller. Karl Popper:A Centenary Assessment (em inglês). London: Ashgate Publishing. 219 páginas. ISBN 9780754653752. Consultado em 10 de junho de 2008
- ↑ Beed, Clive; Kane, Owen (1991). «What Is the Critique of the Mathematization of Economics?». Kyklos. 44 (4): 581–612. doi:10.1111/j.1467-6435.1991.tb01798.x
- ↑ Friedman, Milton (1953). Essays in Positive Economics (em inglês). Chicago: University of Chicago Press. pp. 30, 33, 41. ISBN 9780226264035
- ↑ Keynes, John Maynard (1936). The General Theory of Employment, Interest and Money (em inglês). Cambridge: Macmillan. 297 páginas. ISBN 0333107292
- ↑ Paul A. Samuelson (1952). "Economic Theory and Mathematics — An Appraisal," American Economic Review, 42(2), pp. 56, 64-65 (press +) (em inglês).
- ↑ D.W. Bushaw and R.W. Clower (1957). Introduction to Mathematical Economics, p. vii. (em inglês)
- ↑ Solow, Robert M. (20 de março de 1988). «The Wide, Wide World Of Wealth (The New Palgrave: A Dictionary of Economics'. Edited by John Eatwell, Murray Milgate and Peter Newman. Four volumes. 4,103 pp. New York: Stockton Press. $650)». New York Times (em inglês)
Notas[editar | editar código-fonte]
- Este artigo foi inicialmente traduzido, total ou parcialmente, do artigo da Wikipédia em inglês cujo título é «Mathematical economics».








