Coordenadas hiperbólicas
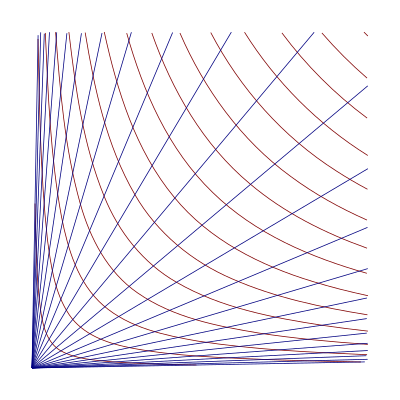
Em matemática, as coordenadas hiperbólicas são um método útil para a localização de pontos no primeiro quadrante do plano cartesiano[porquê?].
As coordenadas hiperbólicas assumem valores tais que
Para um ponto em temos
e
O parâmetro algumas vezes é chamado ângulo hiperbólico e a média geométrica.
A transformação inversa é
Esta é uma transformação contínua, mas não é uma função analítica.
Modelo quadrante para a geometria hiperbólica[editar | editar código-fonte]
A correspondência
proporciona a estrutura de geometria hiperbólica a Q, que é projetada sobre HP por movimentos hiperbólicos. As linhas hiperbólicas de Q são retas que partem da origem ou curvas em forma de pétala que saem e entram pela origem. O deslocamento da esquerda para a direita de HP corresponde a um mapeamento comprimido aplicado a Q. Note que as hipérboles de Q não representam geodésicas neste modelo.
Caso se considere apenas a topologia euclidiana do plano e a topologia herdada por Q, então a fronteira de Q parece próxima a P. O espaço métrico HP mostra que o conjunto aberto Q possui apenas a origem como fronteira, quando visto como o modelo quadrante do plano hiperbólico. De fato, considere "raios" a partir da origem de Q e suas imagens, que são os raios verticais da fronteira R de HP. Qualquer ponto de HP está a uma distância infinita do ponto p no pé da normal a R, mas uma seqüência de pontos desta perpendicular pode tender à direção de p. A seqüência correspondente em Q tende ao longo de um raio em direção à origem. A velha fronteira euclidiana de Q é irrelevante para o modelo quadrante.
Aplicações às ciências físicas[editar | editar código-fonte]
Relações com unidades físicas, como:
- E = IR: Lei de Ohm
- P = VI: Potência elétrica
- PV = kT: Lei do gás ideal
- f λ = c: Ondas senoidais
todas sugerindo a análise cuidadosa dos eixos coordenados. Por exemplo, na termodinâmica o processo isotérmico segue explicitamente o caminho hiperbólico e o trabalho pode ser interpretado como uma variação do ângulo hiperbólico. Da mesma forma, um processo isobárico pode resultar numa hipérbole no eixo temperatura versus densidade absoluta do gás.
Para ver as coordenadas hiperbólicas na teoria da relatividade, ver a seção História abaixo.
Aplicações à estatística[editar | editar código-fonte]
- Estudos comparativos da densidade populacional começam com a escolha de um país, região ou área urbana de referência, cuja população e área são tomados como o ponto (1,1).
- Análises dos representantes políticos de uma região sob regime democrático começa com a escolha de um padrão de comparação: um grupo particular representativo, cuja magnitude e ardósia magnitude (de representantes) é de (1,1) no gráfico.
Aplicações à economia[editar | editar código-fonte]
Há muitas aplicações naturais das coordenadas hiperbólicas na economia:
- Análise da flutuação da taxa de câmbio monetária:
A unidade monetária é definida por O preço da moeda corresponde ao valor Para
encontramos um ângulo hiperbólico positivo. Para uma flutuação toma-se um novo preço
Então a variação em u é:
A quantificação da flutuação da taxa de câmbio através de um ângulo hiperbólico fornece uma medida objetiva, simétrica e consistente. A quantidade é o comprimento do deslocamento da esquerda para a direita do ponto de vista do movimento hiperbólico da flutuação da moeda.
- Análise da inflação ou deflação de preços da cesta básica.
- Quantificação da alteração na cota de mercado de duopólio.
- Fotografia corporativa versus recompra de ações.
História[editar | editar código-fonte]
Enquanto a média geométrica é um conceito antigo, o ângulo hiperbólico é contemporâneo com o desenvolvimento do logaritmo, a última parte do século XVII. Grégoire de Saint-Vincent, Marin Mersenne e Alphonse Antonio de Sarasa avaliaram a quadratura da hipérbole como uma função com propriedades agora familiares com o logaritmo e em seguida com a função exponencial, o seno hiperbólico e cosseno hiperbólico. Como a teoria da função complexa referia-se às séries infinitas, as funções circulares seno e cosseno pareciam absorver o seno e o cosseno hiperbólicos como dependente de uma variável imaginária. No século XIX, os biquatérnios começaram a ser utilizados e mostraram um plano complexo alternativo chamado números hipercomplexos, onde o ângulo hiperbólico é levado a um nível igual ao ângulo clássico. Na literatura inglesa, os biquatérnios foram utilizados para modelar o espaço-tempo e mostrar suas simetrias. Nela, o parâmetro ângulo hiperbólico veio a ser chamado de rapidez. Para os relativistas, examinando-se o quadrante como um futuro possível entre fótons de direções opostas, o parâmetro média geométrica é temporal.
Na relatividade, o foco está na hiper-superfície tridimensional dentro do futuro do espaço-tempo, onde várias velocidades chegam após um tempo próprio dado. Scott Walter[1] explica que em novembro de 1907 Herman Minkowski especulou sobre uma conhecida geometria tridimensional hiperbólica enquanto falava para a Göttingen Mathematical Society, mas não para uma de quatro dimensões.[2] Em homenagem a Wolfgang Rindler, o autor do livro-texto padrão de nível universitário sobre relatividade, as coordenadas hiperbólicas do espaço-tempo são chamadas de coordenadas de Rindler.
Referências[editar | editar código-fonte]
- Betounes, David (2001). Differential Equations. Theory and Applications (em inglês). [S.l.]: Springer-TELOS. p. 254. ISBN 0387951407
- Scott Walter (1999). "The non-Euclidean style of Minkowskian relativity". Chapter 4 in: Jeremy J. Gray (ed.), The Symbolic Universe: Geometry and Physics 1890-1930, pp. 91–127. Oxford University Press. ISBN 0198500882.

















