Lei de Ohm

A Lei de Ohm (por vezes referida como Primeira Lei de Ohm), afirma que, para um condutor mantido à temperatura constante, é também constante a razão entre a tensão entre dois pontos e a corrente elétrica. Essa constante é denominada de resistência elétrica.[1] Lei designada em homenagem ao seu formulador, o físico alemão Georg Simon Ohm (1789-1854).[2]
Lei de Ohm[editar | editar código-fonte]
Quando essa lei é respeitada por um determinado condutor mantido à temperatura constante, este é denominado condutor ôhmico. A resistência de um dispositivo condutor é dada pela equação:[3]
Nesta expressão, é a diferença de potencial elétrico, é a corrente elétrica e é a resistência.
Essa expressão não depende da natureza do condutor: ela é válida para todos os condutores. Para um dispositivo condutor que obedeça à lei de Ohm, a diferença de potencial aplicada é proporcional à corrente elétrica, isto é, a resistência é independente da diferença de potencial e da corrente. Um exemplo de dispositivo que obedece à essa lei — muito utilizado em aparelhos eletrônicos como rádios, televisores e amplificadores — é o resistor. Sua função é controlar a intensidade de corrente elétrica que passa pelo aparelho.[4]
Entretanto, para alguns materiais como os semicondutores, a resistência elétrica não é constante. Mesmo que a temperatura seja, ela depende da diferença de potencial . Estes materiais são denominados condutores não ôhmicos. Um exemplo de componente eletrônico que não obedece à lei de Ohm é o diodo.
Interpretação da resistência elétrica[editar | editar código-fonte]
A resistência elétrica pode ser entendida como a dificuldade de se estabelecer uma corrente elétrica num determinado condutor. Por exemplo, um fio de nicromo precisa ser submetido a uma diferença de potencial elétrico de 300 V para que seja estabelecida uma corrente de 1 A, enquanto um fio de tungstênio precisa ser submetido a apenas 15 V para que nele se estabeleça a mesma corrente. Isto significa que a resistência elétrica do nicromo é maior do que a do tungstênio:[5]
Determinação da resistência[editar | editar código-fonte]
A resistência elétrica de um condutor homogêneo, e de seção transversal constante, é proporcional ao seu comprimento , inversamente proporcional à sua área transversal e depende da temperatura e do material de que é feito o condutor:[5][6]
Essa relação é comumente denominada de Segunda Lei de Ohm. A grandeza chama-se resistividade elétrica e é característica do material e da temperatura. Sua unidade de medida é o ohm-metro ( m). Ela é inversamente proporcional à condutividade elétrica .
Formulação microscópica[editar | editar código-fonte]
Em um condutor metálico isolado, os elétrons estão num estado de movimento aleatório, não apresentando deslocamento preferencial, em média, em nenhuma direção. Se este condutor tem seus terminais ligados aos de uma bateria, um campo elétrico é criado em todos os pontos no interior do condutor e atua sobre os elétrons de forma a produzir um movimento de arrasto, que é a corrente elétrica. Em condutores ôhmicos, o vetor densidade de corrente elétrica , cujo módulo é igual à corrente elétrica dividida pela área de seção transversal, (quando a corrente é uniformemente distribuída pelo condutor), é proporcional ao campo elétrico .[6] O fator de proporcionalidade entre a densidade de corrente e o campo elétrico é a condutividade elétrica :
Esta é a relação microscópica equivalente à relação macroscópica . Pode-se dizer também que um material condutor obedece à lei de Ohm se a condutividade for independente de e de .
A unidade de medida da condutividade é o siemens por metro (S/m). Materiais que conduzem melhor a corrente elétrica são aqueles que possuem os valores mais altos de . A prata, o cobre e o alumínio, por exemplo, são bons condutores, enquanto a mica e o vidro são maus condutores.[1]
A relação macroscópica da lei de Ohm a partir da relação microscópica[editar | editar código-fonte]
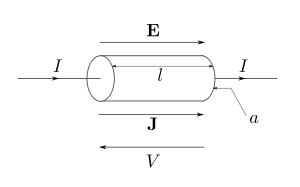
A relação macroscópica pode ser obtida da relação microscópica a partir do seguinte exemplo.[3]
Considere um segmento de fio condutor de comprimento e seção reta , com uma corrente . Para que o campo elétrico não varie apreciavelmente, o segmento do fio deve ser muito pequeno. Sendo o campo elétrico dirigido da esquerda para a direita, o potencial é mais baixo neste lado do que no outro, de forma que se tem
onde é o módulo do campo elétrico. A corrente no condutor é igual ao produto da densidade de corrente pela área de seção reta:
onde usou-se a lei de Ohm na forma microscópica na passagem anterior. Sendo assim,
substituindo por , obtém-se
A expressão entre parênteses pode ser definida como:
e, então, obtém-se a relação
Variação da resistividade e condutividade com a temperatura[editar | editar código-fonte]
Nos metais, os elétrons da última camada eletrônica estão fracamente ligados a átomos individuais, podendo mover-se livremente. Quando a temperatura aumenta, a amplitude do movimento dos íons da rede cristalina também aumenta, o que dificulta a locomoção dos elétrons livres. Em outras palavras, isto quer dizer que a resistividade aumenta com a temperatura. Para uma ampla gama de substâncias, esse aumento é linear, dentro de uma larga faixa de temperaturas. Isto pode ser descrito pela seguinte equação:[7]
onde:
- é a resistividade à temperatura ,
- é a resistividade à temperatura e
- é o coeficiente de temperatura da resistividade e é positivo para os metais.
Temos também a relação da condutividade (σ) com a temperatura do filamento que obedece uma relação inversamente proporcional,[8] uma vez que a condutividade e inversamente proporcional a resistividade (ρ).[9]
Nos semicondutores a resistividade diminui com o aumento da temperatura. Isto acontece, porque as flutuações térmicas a altas temperaturas provocam a promoção de elétrons ligados a transportadores de carga livres.[5]
A resistividade de alguns condutores desaparece bruscamente abaixo de uma temperatura crítica, quando estes são resfriados, podendo manter uma corrente por muito tempo sem necessidade do uso de baterias. Esse fenômeno é chamado de supercondutividade e foi divulgado pela primeira vez em 1911 pelo físico holandês Heike Kamerlingh Onnes.[4]
História[editar | editar código-fonte]

Em janeiro de 1781, antes do trabalho de Georg Ohm, Henry Cavendish fez experimentos com potes de Leyden e tubos de vidro de diâmetro e comprimento variados cheios de solução salina. Ele mediu a corrente observando quão forte foi o choque que sentiu ao completar o circuito com seu corpo. Cavendish escreveu que a "velocidade" (corrente) variava diretamente com o "grau de eletrificação" (voltagem). Ele não comunicou seus resultados a outros cientistas na época, e seus resultados eram desconhecidos até que Maxwell os publicou em 1879.
Francis Ronalds delineou "intensidade" (voltagem) e "quantidade" (corrente) para a pilha seca - uma fonte de alta voltagem - em 1814, usando um eletrômetro de folha de ouro. Ele descobriu para uma pilha seca que a relação entre os dois parâmetros não era proporcional sob certas condições meteorológicas.
Ohm fez seu trabalho sobre resistência nos anos 1825 e 1826 e publicou seus resultados em 1827 como o livro Die galvanische Kette, mathematisch bearbeitet ("O circuito galvânico investigado matematicamente"). Ele se inspirou consideravelmente no trabalho de Fourier sobre a condução de calor na explicação teórica de seu trabalho. Para experimentos, ele inicialmente usou pilhas voltaicas , mas depois usou um termopar pois isso forneceu uma fonte de tensão mais estável em termos de resistência interna e tensão constante. Ele usou um galvanômetro para medir a corrente e sabia que a tensão entre os terminais do termopar era proporcional à temperatura da junção. Ele então adicionou fios de teste de comprimento, diâmetro e material variados para completar o circuito. Ele descobriu que seus dados podiam ser modelados por meio da equação
onde x era a leitura do galvanômetro, l era o comprimento do condutor de teste, α dependia da temperatura da junção do termopar e b era uma constante de toda a configuração. A partir disso, Ohm determinou sua lei da proporcionalidade e publicou seus resultados.

Em notação moderna, escreveríamos,
Onde Ԑ é a fem de circuito aberto do termopar, r é a resistência interna do termopar e R é a resistência do fio de teste. Em termos de comprimento do fio, isso se torna,
Onde é R a resistência do fio de teste por unidade de comprimento. Assim, os coeficientes de Ohm são,

A lei de Ohm foi provavelmente a mais importante das primeiras descrições quantitativas da física da eletricidade. Nós consideramos isso quase óbvio hoje. Quando Ohm publicou seu trabalho pela primeira vez, não era esse o caso; os críticos reagiram ao tratamento que deu ao assunto com hostilidade. Eles chamaram seu trabalho de "teia de fantasias nuas" e o Ministro da Educação alemão proclamou que "um professor que pregava tais heresias era indigno de ensinar ciências". A filosofia científica prevalecente na Alemanha na época afirmava que os experimentos não precisam ser realizados para desenvolver uma compreensão da natureza porque a natureza é muito bem ordenada e que as verdades científicas podem ser deduzidas apenas pelo raciocínio. Além disso, o irmão de Ohm, Martin, um matemático, estava lutando contra o sistema educacional alemão. Esses fatores dificultaram a aceitação do trabalho de Ohm, e seu trabalho não foi amplamente aceito até a década de 1840. No entanto, Ohm recebeu reconhecimento por suas contribuições para a ciência muito antes de morrer. Na década de 1850, a lei de Ohm era conhecida como tal e amplamente considerada comprovada, e alternativas, como a "lei de Barlow", foram desacreditadas, em termos de aplicações reais ao projeto de sistemas telegráficos, conforme discutido por Samuel FB Morse em 1855.
O elétron foi descoberto em 1897 por J. J. Thomson, e rapidamente percebeu-se que é a partícula (portadora de carga) que carrega correntes elétricas em circuitos elétricos. Em 1900, o primeiro modelo ( clássico ) de condução elétrica, o modelo de Drude, foi proposto por Paul Drude, que finalmente deu uma explicação científica para a lei de Ohm. Neste modelo, um condutor sólido consiste em uma rede estacionária de átomos (íons), com elétrons de condução movendo-se aleatoriamente nela. Uma tensão em um condutor causa um campo elétrico, que acelera os elétrons na direção do campo elétrico, causando um deslocamento de elétrons que é a corrente elétrica. No entanto, os elétrons colidem e se dispersam dos átomos, o que torna seu movimento aleatório, convertendo em calor a energia cinética adicionada ao elétron pelo campo (energia térmica). Usando distribuições estatísticas, pode-se mostrar que a velocidade média de deriva dos elétrons e, portanto, a corrente, é proporcional ao campo elétrico e, portanto, à voltagem, em uma ampla faixa de voltagens.
O desenvolvimento da mecânica quântica na década de 1920 modificou um pouco esse quadro, mas nas teorias modernas a velocidade média de deriva dos elétrons ainda pode ser mostrada como sendo proporcional ao campo elétrico, derivando assim a lei de Ohm. Em 1927, Arnold Sommerfeld aplicou a distribuição quântica de energias de elétrons de Fermi-Dirac ao modelo de Drude, resultando no modelo de elétrons livres . Um ano depois, Felix Bloch mostrou que os elétrons se movem em ondas (elétrons de Bloch) através de uma rede de cristal sólido, portanto, espalhar os átomos da rede como postulado no modelo de Drude não é um processo importante; os elétrons espalham átomos de impureza e defeitos no material. O sucessor final, a moderna teoria de banda quântica de sólidos, mostrou que os elétrons em um sólido não podem assumir nenhuma energia como assumida no modelo de Drude, mas estão restritos a bandas de energia, com lacunas entre elas de energias que os elétrons são proibidos de ter. O tamanho do gap é uma característica de uma determinada substância que tem muito a ver com sua resistividade elétrica, explicando por que algumas substâncias são condutores elétricos, algumas semicondutores e alguns isolantes .
Enquanto o antigo termo para condutância elétrica, o mho (o inverso da unidade de resistência ohm), ainda é usado, um novo nome, o siemens, foi adotado em 1971, em homenagem a Ernst Werner von Siemens. O siemens é preferido em documentos formais.
Na década de 1920, foi descoberto que a corrente através de um resistor prático na verdade tem flutuações estatísticas, que dependem da temperatura, mesmo quando a tensão e a resistência são exatamente constantes; esta flutuação, agora conhecida como ruído Johnson-Nyquist, é devido à natureza discreta da carga. Este efeito térmico implica que as medições de corrente e tensão que são feitas em períodos de tempo suficientemente curtos produzirão relações de V / I que flutuam do valor de R implícito pela média de tempo ou média do conjunto da corrente medida; A lei de Ohm permanece correta para a corrente média, no caso de materiais resistivos comuns.
O trabalho de Ohm precedeu em muito as equações de Maxwell e qualquer compreensão dos efeitos dependentes da frequência em circuitos CA. Desenvolvimentos modernos na teoria eletromagnética e na teoria do circuito não contradizem a lei de Ohm quando são avaliados dentro dos limites apropriados.
Modelo microscópico clássico para a condutividade elétrica de metais[editar | editar código-fonte]
Em um metal, os elétrons que não estão presos aos átomos e podem movimentar-se livremente são chamados elétrons de condução.[6] Classicamente, a velocidade quadrática média de agitação térmica dos elétrons à temperatura pode ser estimada via Teorema da equipartição:[7]
Ou seja,
Nesta equação
- é o valor médio do quadrado da velocidade dos elétrons devido a agitação térmica,
- é a massa do elétron e
- é a constante de Boltzmann.
Na ausência de um campo elétrico externo, o movimento dos elétrons no metal é caótico e o valor da velocidade de agitação térmica obtido mostra que esse movimento é muito rápido. Entretanto, se um campo elétrico externo constante é aplicado, os elétrons passam a se deslocar, em velocidade muitíssimo pequena, na direção oposta a do campo, devido à sua carga negativa. Consequentemente, eles experimentam uma aceleração devido à força elétrica , onde é a carga do elétron em módulo. De acordo com a segunda lei de Newton,
ou
onde
- é a aceleração do elétron.
À primeira vista, parece que, como as cargas estão sendo aceleradas, a corrente está aumentando com o tempo, e a lei de Ohm afirma que um campo elétrico constante produz uma corrente constante, o que implica uma velocidade constante. Isto parece contradizer o argumento anterior.[10]
Entretanto, as frequentes colisões dos elétrons que acontecem ao longo do fio fazem com que eles sofram desaceleração. Desta forma, mesmo que eles estejam se acelerando entre as colisões, o resultado global é uma velocidade média constante. Após uma colisão, essa velocidade varia em média de , em que é o tempo médio entre duas colisões, representado por e é a distância média percorrida pelo elétron entre duas colisões, conhecida como livre caminho médio.
O valor médio da velocidade devida a ação do campo elétrico será dada, então, por
A velocidade pode ser expressa em termos da densidade de corrente elétrica :
onde é o número de elétrons livres por unidade de volume e o sinal de menos é devido ao fato de que as cargas em movimento são negativas. Igualando este resultado ao anterior, obtém-se
ou
em que vê-se que a densidade de corrente induzida é proporcional ao campo elétrico , assim como na lei de Ohm. Entretanto, não se pode afirmar que a quantidade seja um bom modelo para a condutividade elétrica de metais, já que a dedução apresentada aqui foi baseada em argumentos puramente clássicos. Por exemplo, experiências mostram que a altas temperaturas, a resistividade elétrica desses materiais varia linearmente com a temperatura e o modelo aqui apresentado implica numa variação proporcional a devido ao termo no denominador da expressão anterior. Ainda assim, o modelo clássico de movimento de arrasto na presença de campo elétrico superposto ao movimento aleatório térmico devido a colisões com átomos do material, conhecido como modelo de Drude, apresenta os ingredientes básicos que definem a condutividade. Um tratamento adequado para o problema da condutividade elétrica em metais é dado pela Mecânica Quântica.
Potência dissipada num resistor[editar | editar código-fonte]
Quando um resistor é percorrido por uma corrente elétrica , devida a uma tensão fornecida por uma fonte de energia, ele se aquece. Esse aquecimento, chamado de efeito Joule, é resultado da transformação da energia que vem da fonte em energia térmica no resistor. A energia transformada em calor por unidade de tempo é a potência dissipada[4] e é calculada pela equação
A unidade de medida da potência é o watt (W).
Usando , obtém-se
Outra relação envolvendo potência e resistência elétrica também pode ser obtida usando :
Por terem essa finalidade de transformar energia elétrica em energia térmica, os resistores também estão presentes nos aquecedores elétricos de ambiente, nos chuveiros elétricos, nos ferros elétricos de passar roupa, nos soldadores elétricos etc.[5]
Ver também[editar | editar código-fonte]
- Campo elétrico
- Diodo semicondutor
- Lei de Joule
- Resistor
- Semicondutor
- Supercondutividade
- Tensão elétrica
Referências
- ↑ a b Alonso e Finn Física um curso universitário Vol 2 - Campos e Ondas Editora Edgard Blucher (1972), págs 150-151
- ↑ «Primeira lei de Ohm: o que diz, fórmula, cálculo». Mundo Educação. Consultado em 3 de março de 2023
- ↑ a b Tipler Física 2 Guanabara dois (1978), págs 792-793
- ↑ a b c Sampaio e Calçada Universo da Física 3 Ondulatória Eletromagnetismo Física Moderna, Atual Editora, segunda edição (2005), págs 45 e 59
- ↑ a b c d Gualter Newton Helou Física Ensino Médio Vol 3, Primeira edição, Editora Saraiva (2010), págs 114-115, 119, 121
- ↑ a b c Halliday e Resnick Física 2 Vol 1, Livros técnicos e científicos editora S.A (1976), págs 133, 135, 144-147
- ↑ a b Nussenzveig H. Moysés Eletromagnetismo Curso de Física Básica 3, Primeira edição (1997), Editora Blucher, págs 105-107
- ↑ Bagnato e Rodrigues, Vanderlei e Vinícius (2006). «Análogo mecânico para condutividade elétrica dos metais:Efeito da temperatura» (PDF). Revista Brasileira de Ensino de Física
- ↑ Girotto e Santos, Emerson e Ivair (2002). «MEDIDAS DE RESISTIVIDADE ELÉTRICA DC EM SÓLIDOS: COMO EFETUÁ-LAS CORRETAMENTE» (PDF). Revista Quim. Nova
- ↑ Griffitts David J. Eletrodinâmica, terceira edição, Person (2011), págs 198-199 e 201




























![{\displaystyle \rho =\rho _{0}[{1}+{\alpha \,(T-T_{0})}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c60ee21bed92bd869036b97159c3bc71502617aa)





































