Integral de Riemann

No ramo da matemática conhecido como análise real, a integral de Riemann, criada por Bernhard Riemann, foi a primeira definição rigorosa de uma integral de uma função em um intervalo. Enquanto a integral de Riemann é inadequada para muitos propósitos teóricos, ela é uma das definições mais fáceis de integral. Algumas deficiências destas técnicas podem ser remediadas pela integral de Riemann-Stieltjes, e a maioria delas desaparece na integral Lebesgue.

Visão geral

Figura 2

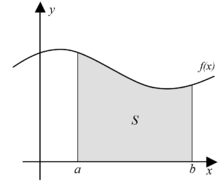
Seja $f(x)$ uma função não negativa válida para os números reais do intervalo $[a,b]$, e seja $S=\{(x,y);0<y<f(x)\}$ uma região plana sob a função $f(x)$ e acima do intervalo $[a,b]$ (veja a figura 2). O nosso interesse é medir a área de $S$. Uma vez realizada esta medição, iremos denotá-la por:

$\int \limits _{a}^{b}f(x)\,dx$

A ideia básica de integral de Riemann é muito simples de usar e não deixa ambiguidade para a área de $S$. Para se ter uma aproximação cada vez melhor, nós podemos dizer que "no limite" iremos obter exatamente a área de $S$ sob a curva.

Note que onde $f$ pode ser positivo e negativo, a integral corresponde à "área com sinal"; isto é, a área acima do eixo $x$ é positiva e a área abaixo do eixo $x$ negativa.

Uma soma de Riemann. O número na parte superior representa a soma das áreas dos retângulos azuis. O valor converge para o integral da função.

Definição da integral de Riemann

Partições de um intervalo

Uma partição de um intervalo $[a,b]$ é uma sequência finita $a=x_{0}<x_{1}<x_{2}<\ldots <x_{n}=b$. Cada $[x_{i},x_{i+1}]$ é denominado como um sub-intervalo da partição. A malha de uma partição é definida como o comprimento do mais longo sub-intervalo $[x_{i},x_{i+1}]$, isto é, aquele em que $\max(x_{i+1}-x_{i})$ onde $0\leq i\leq n-1$. Isto também é conhecido como norma de partição.

Uma partição de um intervalo etiquetado é uma partição de um intervalo juntamente com uma sequência finita de números $t_{0},\ldots ,t_{n-1}$ sujeito a condição que para cada $i$, $x_{i}\leq t_{i}\leq x_{i+1}$. Em outras palavras, isto é uma partição juntamente com um ponto distinto para cada sub intervalo. A malha de uma etiqueta é definida da mesma forma que para uma partição ordinária.

Suponha que $x_{0},\ldots ,x_{n}$ juntamente com $t_{0},\ldots ,t_{n-1}$ são uma partição etiquetada de $[a,b]$, e que $y_{0},\ldots ,y_{m}$ juntamente com $s_{0},\ldots ,s_{m-1}$ seja uma outra partição etiquetada de $[a,b]$. Nos poderemos dizer que $y_{0},\ldots ,y_{m}$ e $s_{0},\ldots ,s_{m-1}$ juntas são um refinamento da $x_{0},\ldots ,x_{n}$ juntamente com $t_{0},\ldots ,t_{n-1}$ se para cada inteiro $i$ com $0\leq i\leq n$, exista um inteiro $r(i)$ tal que $x_{i}=y_{r(i)}$ e tal que $t_{i}=s_{j}$ para algum $j$ com $r(i)\leq j\leq r(i+1)$. Falando de uma maneira mais simples, um refinamento de uma partição de etiqueta pega uma partição inicial e adiciona mais etiquetas, mas isto não chega a lugar algum.

Nos podemos definir uma ordem parcial um subconjunto de todas as etiquetas de partição significando que uma etiqueta de partição é maior do que outra se a maior é um refinamento da menor.

Soma de Riemann

Escolha uma função válida para números reais $f$ a qual se encontra definida no intervalo $[a,b]$. A Soma de Riemann de $f$ com respeito a partição denominada $x_{0},\ldots ,x_{n}$ com $t_{0},\ldots ,t_{n-1}$ é:

$\sum _{i=0}^{n-1}f(t_{i})(x_{i+1}-x_{i})$

Cada termo na soma é o produto do valor da função em um ponto dado e o comprimento do intervalo. Consequentemente, cada termo representa área de um retângulo com a altura $f(t_{i})$ e o comprimento $x_{i+1}-x_{i}$. A soma de Riemann é a área sinalizada de todos os retângulos.

A integral de Riemann

Grosseiramente falando, a integral de Riemann é o limite da soma de Riemann com uma função de partição que se afine cada vez mais. Contudo, o significado preciso a cerca do que significa "cada vez mais fino" é o mais importante.

Um fato importante é que a malha de partição deve ser tornar menor e menor, até que seu limite atinja zero. Se isto não for assim, então não poderemos ter uma boa aproximação para esta função em certos intervalos. De fato, isto é suficientemente bom para definir uma integral. Para ser especifico, nos dizemos que a integral Riemann de $f$ se igualara a $S$ se as seguintes condições foram consideradas:

Para todo $\epsilon >0$, onde exista $\delta >0$ tal que para qualquer partição etiquetada $x_{0},\ldots ,x_{n}$ e $t_{0},\ldots ,t_{n-1}$ onde a malha seja menor que $\delta$, nos temos:

$\left|\sum _{i=0}^{n-1}f(t_{i})(x_{i+1}-x_{i})-s\right|<\epsilon .\,$

Contudo, existe um problema desagradável com esta definição: ela é muito difícil para se trabalhar. Então faremos uma definição alternativa para a integral de Riemann a qual seja mais fácil para se trabalhar, então se prova que esta é a mesma definição que a original. Nossa nova definição diz que a integral de Riemann de $f$ é igual a $s$ se as seguintes condições foram consideradas:

Para todo $\epsilon >0$, existe uma partição etiquetada $x_{0},\ldots ,x_{n}$ e $t_{0},\ldots ,t_{n-1}$ tal que para qualquer refinamento $y_{0},\ldots ,y_{m}$ e $s_{0},\ldots ,s_{m-1}$ de $x_{0},\ldots ,x_{n}$ e $t_{0},\ldots ,t_{n-1}$, nos teremos

$\left|\sum _{i=0}^{m-1}f(s_{i})(y_{i+1}-y_{i})-s\right|<\epsilon .\,$

Ambos eventualmente significam, a soma de Riemann de $f$ com respeito para qualquer partição que seja selecionada que leve a se aproximar de $s$. Desde que isto seja verdade, não importa a proximidade que necessitamos que esta soma ira assumir, nos diremos que a soma Riemann convergira para $s$. Esta definição é sempre um caso especial de um conceito mais geral, uma rede.

Como nos estabelecemos antes, estas duas definições são equivalentes. Em outras palavras, $s$ funciona na sua primeira definição se e somente se $s$ funciona na sua segunda definição. Para mostrar que a primeira definição implica a segunda, iniciamos com um $\epsilon$, e escolhemos um $\delta$ que satisfaça a condição. Escolha qualquer partição etiquetada onde a malha é menor que $\delta$. Esta soma Riemann é em dentro $\epsilon$ de $s$, e qualquer refinamento desta partição ira também ter uma grade menor que $\delta$, então a soma de Riemann dos refinamentos ira também estar em $\epsilon$ de $s$. Para mostrar que a segunda definição implica a primeira, isto é facilitado com uso da integral de Darboux. Primeiro mostraremos que a segunda é equivalente a definição da integral de Darboux, para isto veja a integral. Agora nos iremos mostras que a função de integração de Darboux satisfaz a primeira definição. Escolha a partição $x_{0},\ldots ,x_{n}$ tal que o limite inferior e superior da soma de Darboux com respeito a esta partição esteja em dentro ${\frac {\epsilon }{2}}$ do valor $s$ da integral de Darboux. Seja $r$ igual $\max _{0\leq i\leq n-1}M_{i}-m_{i}$, onde $M_{i}$ e $m_{i}$ são o supremum e infimum, respectivamente, de $f$ em $[x_{i},x_{i+1}]$, e sendo $\delta$ menor que ${\frac {\epsilon }{2rn}}$ e $\min _{0\leq i\leq n-1}x_{i+1}-x_{i}$. Então não é difícil de mostrar que a soma de Riemann de $f$ com respeito de qualquer partição etiquetada da grade menor que $\delta$ ira estar em dentro de ${\frac {\epsilon }{2}}$ da maior ou menor soma de Darboux, então isto estará em dentro de $\epsilon$ de $s$.

Referências

• * Shilov, G. E., and Gurevich, B. L., 1978. Integral, Measure, and Derivative: A Unified Approach, Richard A. Silverman, trans. Dover Publications. ISBN 0-486-63519-8.

Ver também

• Primitiva
• Integral de Riemann-Stieltjes
• Integral de Henstock–Kurzweil
• Integral de Lebesgue
• Integral de Darboux