Soma de Riemann

Quatro dos métodos do somatório de Riemann para aproximação da área sob curvas. Métodos à direita e à esquerda fazem a aproximação usando os pontos finais à direita e à esquerda de cada subintervalo, respectivamente. Métodos máximo e mínimo fazem a aproximação usando o maior e menor valores de pontos finais de cada subintervalo, respectivamente. Os valores das somas convergem como os subintervalos da metade superior à esquerda a baixo à direita.

Na matemática, a soma de Riemann é uma aproximação obtida pela expressão $\sum _{i=1}^{n}f(x_{i}^{*})\cdot \Delta x$.

É nomeada em homenagem ao matemático alemão Bernhard Riemann. Uma aplicação muito comum é a aproximação da área de funções ou linhas em um gráfico, mas também o comprimento das curvas e outras aproximações.

A soma é dada pela divisão da região a ser calculada em formas (retângulos, trapézios, parábolas ou cubos) que juntos formam uma região que é similar àquela a ser medida, então calcula-se a área de cada uma das formas, e finalmente soma-se todas essas áreas menores juntas.  Essa abordagem pode ser usada para encontrar uma aproximação numérica para a integral definida mesmo se o teorema fundamental do cálculo não ajudar a encontrar uma forma fechada.

Tendo em vista que a região preenchida pelas formas menores geralmente não corresponde a exata forma da região a ser medida, a Soma de Riemann será diferente desta. Esse erro pode ser reduzido se a região for mais dividida, usando formas cada vez menores. Ao passo que as formas ficam menores, a soma se aproxima a Integral de Riemann.

Normalmente a Soma de Riemann tem uma aplicação ótima para funções polinomiais ou algébricas, o que significa que é possível precisar o valor exato do limite da soma com facilidade. Porém, para funções ditas transcendentes o cálculo da integral definida é não trivial por Riemann, ocorrendo ele comumente pela formação de retângulos de forma análoga ao método da exaustão.

Definição

Considere f:D → R sendo uma função definida do subconjunto D, de números reais, R. Tome I = [a, b] como um intervalo fechado contido em D, e

$P=[x_{0},x_{1}],[x_{1},x_{2}],...,[x_{n-1},x_{n}],$

sendo uma partição de I, onde

$a=x_{0}<x_{1}<x_{2}<...<x_{n}=b.$

Uma soma de Riemann de f sobre I com a partição P é definida como

$S=\sum _{i\mathop {=} 1}^{n}f(x_{i}^{*})(x_{i}-x_{i-1}),x_{i-1}\leq x_{i}^{*}\leq x_{i}.$

Atenção no uso de “uma” ao invés de “a” em referência a soma de Riemann. Isso ocorre pelo fato que a escolha de $x_{i}^{*}$  no intervalo $[x_{i-1},x_{i}]$  é arbitrária, dado o fato que qualquer função f definida em um intervalo I e na partição fixada P, pode produzir uma soma de Riemann diferente em decorrência de qual $x_{i}^{*}$ foi escolhido, desde que $x_{i-1}\leq x_{i}^{*}\leq x_{i}$ se mantenha verdadeiro.

Exemplo: Escolhas específicas de $x_{i}^{*}$ nos dão diferentes tipos de soma de Riemann:

• Se $x_{i}^{*}=x_{i-1}$ para todo i, então S é chamado de Soma de Riemann à Esquerda;
• Se $x_{i}^{*}=x_{i}$ para todo i, então  S é chamado de Soma de Riemann à Direita;
• Se $x_{i}^{*}={\frac {1}{2}}(x_{i}+x_{i-1})$ para todo i, então é S é chamado de Soma de Riemann Média.
• A média entre a Soma à Esquerda e a Soma à Direita é chamada de Soma Trapezoidal.
• Se é dado que $S=\sum _{i\mathop {=} 1}^{n}v_{i}(x_{i}-x_{i-1}),$  onde $v_{i}$ é o supremo de f sobre $[x_{i-1},x_{i}]$ , então S é definido como uma Soma de Riemann Superior;
• De forma semelhante, se $v_{i}$ é o ínfimo de f sobre $[x_{i-1},x_{i}]$ , então S é definido como uma Soma de Riemann Inferior.

Qualquer soma de Riemann em dada partição (isto é, qualquer soma obtida pela escolha de $x_{i}^{*}$ entre $x_{i-1}$ e $x_{i}$ ) está entre as somas de Riemann superior e a inferior. Uma função é definida como integrável por Riemann se a soma inferior e superior forem se aproximando conforme a partição se afina. Este fato pode ser também usado para a integração numérica.

Método

Soma de Riemann à Esquerda

Soma de Riemann à Direita

Os quatro métodos de Riemann para a soma são geralmente melhor usados com partições de tamanhos equivalentes. O intervalo [a, b] é, portanto, dividido em n subintervalos, de comprimento

$\Delta x={b-a \over n}.$   Os pontos na partição serão então $a,a+\Delta x,a+2\Delta x,...,a+(n-2)\Delta x,a+(n-1)\Delta x,b.$

Soma de Riemann à Esquerda

Para a Soma de Riemann à Esquerda, aproxima-se a função pelo seu valor no ponto final à esquerda, dando múltiplos retângulos com base Δx e altura f(a+iΔx). Tomando para i = 0, 1, ... n-1, e adicionando as áreas resultantes temos

$\Delta x{}[f(a)+f(a+\Delta x)+f(a+2\Delta x)+...+f(b-\Delta x)].$

 A soma de Riemann à esquerda resulta em uma superestimação se f está monotonicamente decrescendo nesse intervalo, e em uma subestimação se f está monotonicamente crescendo.

Soma de Riemann à Direita

Nessa soma, aproxima-se f de seu valor no ponto final à direita. São gerados, então, múltiplos retângulos de base Δx e altura f(a+Δx). Tomando para i – 1 , ..., n e adicionando as áreas resultantes se produz

$\Delta x{}[f(a+\Delta x)+f(a+2\Delta x)+...+f(b)].$  

Soma de Riemann Média

A soma de Riemann à direita resulta em uma subestimação se f está monotonicamente decrescendo, e uma superestimação se f está

monotonicamente crescendo. O erro na fórmula será

$\left|\int _{a}^{b}f(x)dx-A_{direita}\right|\leq {\frac {M_{1}(b-a)^{2}}{2n}},$

 onde $M_{1}$ é o valor máximo do valor absoluto de $f'(x)$ nesse intervalo.

Soma de Riemann Regra Trapezoidal

Soma Média

Aproximando f no ponto médio dos intervalos expressam f(a+Δx/2) para o primeiro intervalo, para o próximo temos f(a+3Δx/2), e assim por diante até f(b-Δx/2). Somando as áreas temos

$\Delta x[f(a+{\frac {\Delta x}{2}})+f(a+{\frac {3\Delta x}{2}})+...+f(b-{\frac {\Delta x}{2}})].$ 

O erro dessa formula será

$\left|\int _{a}^{b}f(x)dx-A_{media}\right|\leq {\frac {M_{2}(b-a)^{3}}{24n^{2}}},$

onde $M_{2}$ é o valor máximo do valor absoluto de $f''(x)$ nesse intervalo.

Regra Trapezoidal

Nesse caso, os valores da função f no intervalo são aproximados pela média dos valores nos pontos finais da direita e da esquerda. Dessa mesma maneira, um simples cálculo usando a formula da área

$A={\frac {1}{2}}h(b_{1}+b_{2})$

 para um trapézio de lados paralelos b₁, b₂ e altura h produz

${\frac {1}{2}}\Delta x[f(a)+2f(a+\Delta x)+2f(a+2\Delta x)+2f(a+3\Delta x)+...+2f(b-\Delta x)+f(b)].$

O erro dessa fórmula será

$\left|\int _{a}^{b}f(x)dx-A_{trap}\right|\leq {\frac {M_{2}(b-a)^{3}}{12n^{2}}},$

 onde $M_{2}$ é o valor máximo do valor absoluto de $f''(x).$

 A aproximação obtida com a regra do trapézio para a função é o mesmo que a média da somas esquerdas e direitas dessa função.

Exemplo

O valor da Soma de Riemann sob a curva y=x² de 0 à 2. Conforme o número de retangulos aumenta, aproxima-se da área exata de 8/3

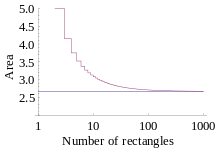
Tomado um exemplo, a área sob a curva de y=x² entre 0 e 2 pode ser processualmente computada usando o método de Riemann.

O intervalo [0,2] é primeiramente dividido em n subintervalos, cada um deles com comprimento de ${\frac {2}{n}}$ ; esse é o comprimento dos retângulos de Riemann (a seguir chamadas “caixas”). Já que será usada a soma de Riemann à direita, a sequência de coordenadas x para as caixas será $x_{1},x_{2},...,x_{n}$. Dessa forma, a sequência de alturas das caixas será $x_{1}^{2},x_{2}^{2},...,x_{n}^{2}$. É um fato importante que $x_{i}={\frac {2i}{n}}$ e $x_{n}=2$.

A área de cada caixa será ${\frac {2}{n}}\times x_{i}^{2}$ e sendo assim a soma de Riemann à direita será: 

${\begin{matrix}S&=&{\frac {2}{n}}\times \left({\frac {2}{n}}\right)^{2}+...+{\frac {2}{n}}\times \left({\frac {2i}{n}}\right)^{2}+...+{\frac {2}{n}}\times \left({\frac {2n}{n}}\right)^{2}\\&=&{\frac {8}{n^{3}}}(1+...+i^{2}+...n^{2})\\&=&{\frac {8}{n^{3}}}\left({\frac {n(n+1)(2n+1)}{6}}\right)\\&=&{\frac {8}{n^{3}}}\left({\frac {2n^{3}+3n^{2}+n}{6}}\right)\\&=&{\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}\end{matrix}}$

Se o limite é visualizado como  n → ∞, pode-se concluir que a aproximação alcança o valor real da área  sob a curva ao passo que o número de caixas aumenta.

Consequentemente:

$\lim _{n\to \infty }S=\lim _{n\to \infty }\left({\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}\right)={\frac {8}{3}}$ .

Esse método concorda com a integral definida tal qual calculada nos modos mais mecânicos:

$\int _{0}^{2}x^{2}dx={\frac {8}{3}}$

Animações

Soma de Riemann à Esquerda

Soma de Riemann à Direita

Soma de Riemann Média

Soma de Riemann para y=x²

Ver também

Integral de Riemann

Integral de Riemann-Stieltjes

Integral de Lebesgue

Fórmula de Simpson

Primitiva

Referências

• Thomas, George B. Jr.; Finney, Ross L. (1996), Calculus and Analytic Geometry (9th ed.), Addison Wesley, ISBN 0-201-53174-7