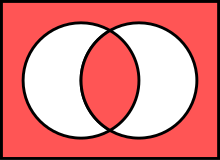
Conectivo lógico bicondicional
Na Lógica e Matemática, a Lógica bicondicional (também conhecida como bicondicional material) é o Conectivo lógico de duas proposições afirmando "p se e somente se q", onde q é uma Hipótese (ou antecedente) e p é um conclusão (ou consequente).[1] Isso é frequentemente abreviado p sse q. O operador é denotado usando uma seta de dupla implicação (↔), a prefixed E (Epq), um sinal de igualdade (=),um sinal de equivalência (≡), ou EQV. Isso é logicamente equivalente a (p → q) ∧ (q → p), ou o XNOR (nor exclusivo) operador da Álgebra_booleana.Isto é equivalente a "(não p ou q) e (não q ou p)". Também é logicamente equivalente a "(p e q) ou (não p e não q)",significando "os dois ou nenhum". A única diferença paraCondicional_material é o caso no qual a hipótese é falsa mas a conclusão é verdadeira. Neste caso, na condicional, o resultado é verdadeiro, contudo, na bicondicional o resultado é falso. Na interpretação conceitual, a = b significa "Todos os a 's são b 's e todos os b 's são a 's"; Em outras palavras, os conjuntos a e b coincidem: eles são idênticos. Isso não significa que todos os conceitos têm o mesmo significado. Exemplos: "triângulo" e "trilateral", "triângulo equiangular" e "triângulo equilátero". O antecedente é o "sujeito" e o consequente é o e predicado de uma afirmativa/ Proposição universal.
Na interpretação proposicional, a ⇔ b significa que a implica b e b implica a; em outras palavras, que as proposições são equivalentes, o que é dizer, ambas são verdadeiras ou falsas ao mesmo tempo. Isso não significa que elas tem o mesmo significado. Exemplo: "O triângulo ABC tem dois lados iguais", e "O triângulo ABC tem 2 ângulos iguais". O antecedente é a premissa ou a causa e o consequente é a consequência. Quando uma implicação é traduzida por um julgamento hipotético (ou condicional) O antecedente é chamado de "hipótese (ou de condição) e o consequente é chamado de tese.
Uma forma comum de se demonstrar um bicondicional é usar sua equivalência para a conjunção de duas condicionais ,em que há uma troca entre a hipótese e a conclusão, as demonstrando separadamente.
Quando ambos os membros da bicondicional são proposições, ela pode ser dividida em duas condicionais, na qual uma é chamada de teoremae a outra é sua recíproca.[carece de fontes]Assim, sempre que um teorema e sua recíproca são verdadeiros, temos um bicondicional. Um simples teorema dá origem a uma implicação cujo antecedente é a hipótese e cujo consequente é a tese do teorema. condição suficiente da tese, e a tese a condição necessária da hipótese; isto é, é suficiente que a hipótese seja verdadeira para a tese de ser verdadeira também; embora seja necessário que a tese seja verdadeira para a hipótese de ser verdade também. Quando um teorema e sua recíproca são verdadeiros, dizemos que a sua hipótese é a condição necessária e suficiente da tese, ou seja, que é ao mesmo tempo, tanto a causa como consequência. Muitas vezes é dito que a hipótese é a condição suficiente da tese, e a tese a condição necessária da hipótese; isto é, é suficiente que a hipótese seja verdadeira para a tese de ser verdadeira também; embora seja necessário que a tese seja verdadeira para a hipótese de ser verdade também. Quando um teorema e sua recíproca são verdadeiros, dizemos que a sua hipótese é a condição necessária e suficiente da tese, ou seja, que é ao mesmo tempo, tanto a causa como consequência.
Definição[editar | editar código-fonte]
Igualdade lógica (Também conhecida como bicondicional) é uma operação em dois valores verdade, tipicamente, o valor de duas proposições, que produzem o valor verdadeirose e somente se ambos os operandos são falsos ou ambos os operandos são verdadeiros.
Tabela verdade[editar | editar código-fonte]
A tabela verdade para (também escritos como A ≡ B, A = B, or A EQ B) como a seguir:
| INPUT | OUTPUT | |
| A | B | A B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Mais de duas proposições combinadas por são ambíguas:
pode estar significando ,
Ou pode ser usado para dizer que todos os são todos verdadeiros ou todos falsos:
Só para o zero ou para dois argumentos isso é o mesmo.
As próximas tabelas verdades mostram o mesmo padrão apenas na linha com nenhum argumento e nas linhas com dois argumentos:
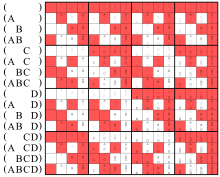
concebido como equivalente a
O diagrama de Venn central abaixo,
e a linha (ABC ) nesta matriz
representam a mesma operação.
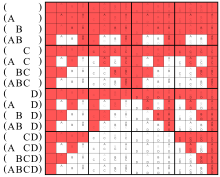
concebido como uma simplificação para
O diagrama de bem exatamente abaixo,
e a linha (ABC )nesta matriz
representam a mesma operação.
The left Venn diagram below, and the lines (AB ) in these matrices represent the same operation.
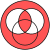
Diagramas de Venn[editar | editar código-fonte]
As áreas vermelhas representam verdadeiro (como em ![]() para Disjunção_lógica|e).
para Disjunção_lógica|e).
|
|
|
Propriedades[editar | editar código-fonte]
Comutatividade: sim
Associatividade: sim

|

|

|
|

|
Distributividade: Bicondicionais dão distribuem entre nenhuma função binária (nem a si mesmo),
Mas a disjunção lógica (veja aqui)se distribui sobre bicondicionais.
Função_monótona: não
monotonicity: no

|

|
|

|
verdade preservada: sim
Quando todas as entradas são verdadeiras, a saída é verdadeira.
falsidade de preservação: não
Quando todos as entradas são falsas, a saída não é falsa.
Walsh spectrum: (2,0,0,2)
Nãolinearidade: 0 (a função é linear)
Regras de inferência[editar | editar código-fonte]
Como todos os conectivos em lógica de primeira ordem, a bicondicional tem regras de inferência que governam seu uso em provas formais.
introdução bicondicional[editar | editar código-fonte]
Introdução_Bicondicional permite inferir que, se B se segue a partir de A, e A Decorre B, então A Se_e_somente_se B. Por exemplo, a partir das declarações "se eu estou respirando, então eu estou vivo" e "se eu estou vivo, então eu estou respirando", pode-se inferir que "eu estou respirando, se e somente se eu estiver vivo "ou, igualmente inferível:" Eu estou vivo, se e somente se eu estou respirando. "
B → A A → B ∴ A ↔ B
B → A A → B ∴ B ↔ A
Eliminação da bicondicional[editar | editar código-fonte]
Eliminação Biconditional permite inferir uma a condicional de um bicondicional: if (A ↔ B) é verdadeira, então pode-se inferir um sentido da bicondicional, (A → B) e (B → A).
Por exemplo, se é verdade que eu estou respirando, se e somente se, eu estou vivo, então é verdade que se eu estou respirando, eu estou vivo, do mesmo modo, é verdade que se eu estou vivo, eu estou respirando . formalmente:
( A ↔ B ) ∴ ( A → B )
também
( A ↔ B ) ∴ ( B → A )
Uso coloquial[editar | editar código-fonte]
Uma maneira inequívoca de afirmar uma bicondicional em português é da forma "b se um e se b". Outra é "a se e somente se b". Um pouco mais formal, pode-se dizer "b implica a e a implica b". Em português "se" pode às vezes ser usado como um bicondicional. É preciso pesar contexto fortemente.
Por exemplo, "eu vou te comprar uma nova carteira, se você precisa de uma" pode ser entendida como uma bicondicional, uma vez que o orador não tem a intenção de um resultado válido para estar comprando a carteira ou não a carteira é necessário (como em uma condicional). No entanto, "está nublado, se está chovendo" não é concebida como um bicondicional, uma vez que pode ser nublado, enquanto não chover.
Ver também[editar | editar código-fonte]
Notas[editar | editar código-fonte]
- ↑ Handbook of Logic, page 81
References[editar | editar código-fonte]
- Brennan, Joseph G. Handbook of Logic, 2nd Edition. Harper & Row. 1961
Predefinição:Logical connectives Este artigo incorpora material de Biconditional do PlanetMath, que é licenciado sob GFDL.