Elementos orbitais
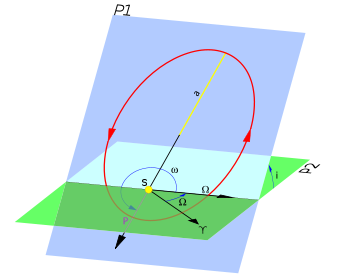
 - Nó ascendente, - Argumento do periastro, - Ponto Vernal, Ω - Longitude do nó ascendente, i - Inclinação orbital do corpo secundário em relação ao plano de referência.
- Nó ascendente, - Argumento do periastro, - Ponto Vernal, Ω - Longitude do nó ascendente, i - Inclinação orbital do corpo secundário em relação ao plano de referência.Os elementos orbitais de um corpo celeste são um conjunto de seis parâmetros que permitem definir a sua órbita em torno de qualquer outro corpo celeste de forma totalmente unívoca. Estas seis quantidades são:[1][2][3][4]
- Longitude do nó ascendente ()
- Inclinação orbital ()
- Argumento do periastro () - se a órbita for em torno do Sol, argumento do periélio
- Semieixo maior da órbita ()
- Excentricidade da órbita ()
- Anomalia média da época ()
Por vezes, no lugar da anomalia média da época, utiliza-se a anomalia média de um certo tempo (), ou a longitude média, ou a anomalia verdadeira ou, mais raramente, a anomalia excêntrica.
Por vezes também a época da passagem pelo periastro substitui a anomalia média. Em lugar do semieixo maior pode-se utilizar também o período orbital.
Pode usar-se a (longitude do periastro), que se relaciona com a longitude do nó ascendente () e com o argumento do periastro () mediante a seguinte expressão:
Os três primeiros elementos orbitais simplesmente são tais que os ângulos de Euler definem a orientação da órbita no espaço, enquanto os restantes três definem a forma da órbita e a posição do corpo na órbita.
- A inclinação e a longitude do nó ascendente indicam o plano da órbita.
- O argumento do periastro orienta a órbita dentro do seu plano.
- O semieixo maior (ou o período, indistintamente) determina o tamanho da órbita.
- A excentricidade determina a sua forma.
- A época da passagem pelo periastro (ou a anomalia média) permitem situar o objeto na sua órbita.
Os seis elementos anteriores surgem no problema dos dois corpos sem perturbações externas. Uma trajetória perturbada realista é representada como uma sucessão instantânea de cónicas que partilham um dos seus focos. Estes elementos orbitais chamam-se osculatrizes e a trajetória é sempre tangente a esta sucessão de cónicas.
Os elementos orbitais de objetos reais tendem a alterar-se ao longo do tempo. A evolução dos elementos orbitais tem lugar devido fundamentalmente à força gravitacional dos outros corpos. No caso de satélites, devido à falta de esfericidade do primário, ou ao atrito com a atmosfera. Isto é fundamental nos satélites artificiais da Terra ou de outros planetas. No caso de cometas, a expulsão de gás e a pressão da radiação, ou as forças eletromagnéticas introduzem pequenas forças não gravitacionais que devem ser consideradas para explicar o seu movimento.
Ver também[editar | editar código-fonte]
Referências
- ↑ CÁLCULO DA VARIAÇÃO DOS ELEMENTOS ORBITAIS DE SATÉLITES LUNARES DEVIDO À DISTRIBUIÇÃO NÃO UNIFORME DE MASSA DA LUA
- ↑ Green, Robin M. (1985). Spherical Astronomy. Cambridge University Press. ISBN 978-0-521-23988-2. (em inglês)
- ↑ Danby, J. M. A. (1962). Fundamentals of Celestial Mechanics. Willmann-Bell. ISBN 978-0-943396-20-0 (em inglês)
- ↑ Isaías Rojas Peña, Astronomía Elemental: Volumen I: Astronomía Básica, Ediciones USM, 2010 ISBN 9-563-32536-2 (em castelhano)
Bibliografia[editar | editar código-fonte]
- M. Asunción Català Poch, Juan José de Orús Navarro, Jorge Núñez de Murga, Astronomía esférica y mecánica celeste, Edicions Universitat Barcelona, 2007 ISBN 8-447-53059-0 (em castelhano)
- Romildo Póvoa Faria, Fundamentos de Astronomia, Papirus Editora, 1987 ISBN 8-530-80491-0
Ligações externas[editar | editar código-fonte]
- «Os elementos orbitais em breve explicação» (em inglês)
- «Elementos orbitais de satélites meteorológicos» 🔗 (em inglês)
- «Tutorial» (em inglês)











