Escala diatônica
Este artigo não cita fontes confiáveis. (Agosto de 2011) |
Escala diatônica é uma escala de sete notas (heptatônica), com cinco intervalos de tons e dois intervalos de semitons entre as notas. Este padrão se repete a cada oitava nota numa seqüência tonal específica. A escala diatônica é típica da música ocidental e concerne à fundação da tradição da música europeia. As escalas modernas maior e menor são diatônicas, assim como todos os sete modos tonais utilizados atualmente.
Histórico[editar | editar código-fonte]
As escalas que hoje em dia são conhecidas como escala maior e escala menor, na Era Medieval e no começo da Renascença, eram apenas dois dos sete modos litúrgicos (modos jônio e eólio, respectivamente). Na passagem da Renascença para o Período Barroco, a noção musical de tonalidade já se consolidava, baseada na ideia de uma tríade central em vez de uma nota simples como tom central de cada modo (finalis). As escalas maiores e menores dominaram a música ocidental até o início do Século XX, parcialmente porque os seus intervalos são perfeitos para reforçar a ideia da tríade central. Entretanto, a sonoridade modal sobreviveu por meio da música tradicional, popular e folclórica, sempre havendo inclusões no repertório erudito desde a era clássica, passando pela romântica (especialmente nos repertórios nacionalistas, novamente marcando a presença da música popular) até a música erudita do Século XX (com compositores como Debussy e Villa-Lobos, a beber dos modos da música oriental e indígena brasileira, respectivamente). A sonoridade modal se reinventou na música popular do século XX, sendo visível na escala do Rock, no Jazz e de maneira mais especial e recente com a chamada World Music, na busca de referências sonoras com a antiguidade e com a história antiga das civilizações (Inca, Índia, China, etc.).
Entretanto, a organização da harmonia da música clássica, a partir do Período Barroco é completamente fundamentada na organização harmônica advinda dos modos jônio e eólio, que fundamentam os dois sistemas harmônicos Maior e Menor.
Teoria da Escala Diatônica[editar | editar código-fonte]
Todas as escalas musicais empregadas na música ocidental não passam de variantes da escala diatônica. Ela teve origem na antiga Grécia.
O sábio grego Pitágoras acreditava que tudo no universo está governado pelos números. Ele notou que, quando uma corda esticada é posta em vibração, ela produz um certo som. Se o comprimento da corda vibrante for reduzido à metade, um som mais agudo é produzido, que guarda uma relação muito interessante com o primeiro. Para entender melhor o que Pitágoras fez, vamos pensar na corda dó de uma viola ou violoncelo moderno. Quando submetida a uma certa tensão, se a corda vibra em toda a sua extensão, ela produz um som de uma certa frequência, que se convencionou chamar de dó. O instrumentista varia o comprimento da corda vibrante, pondo o dedo em certas posições na corda. O que Pitágoras fez foi reduzir o comprimento da corda segundo a sequência de frações , , e . A vibração do comprimento restante (, , e ) produziria as notas que hoje nós chamamos de dó, sol, fá e mi.

Como a frequência do som produzido por uma corda vibrante é inversamente proporcional ao comprimento da corda (), se atribuímos o valor 1 à frequência fundamental da corda, as frequências das outras notas que acabamos de obter resultam: mi = , fá = , sol = . Isso pois os comprimentos para as notas mi, fá e sol são, respectivamente: , e .
Assim, as notas musicais são geradas a partir de relações de números simples com a frequência fundamental. Ao multiplicarmos a frequência de uma nota por 2, obtemos uma outra nota que recebe o mesmo nome da anterior. Se multiplicamos a frequência por , obtemos uma nota que guarda com a anterior uma relação harmônica tão interessante que ela recebe um nome especial: a dominante.
É claro que uma escala musical com só quatro notas como a que obtivemos acima é muito pobre, mas a verdade é que todas as notas musicais podem ser geradas a partir da dominante. Por exemplo, se quisermos saber qual é a dominante do mi, só precisamos multiplicar a frequência do mi por :
* = ; obtivemos assim uma outra nota, que chamamos de si.
Se multiplicarmos a frequência do fá por obteremos a própria nota dó, provando assim que a dominante do fá é dó: * = 2
Já sabemos que sol é a dominante de dó; para saber qual é a dominante do próprio sol, fazemos *=. Obtemos então uma nota mais aguda que o segundo dó; dividindo sua frequência por 2 (para que ela fique na primeira gama que estamos tentando preencher), *= - obtemos assim uma outra nota, que vamos chamar de ré.
Assim, seguindo o método acima, procurando achar a dominante de cada nota obtida (multiplicando sua frequência por 3/2), acabamos por obter a escala diatônica completa:
| dó | ré | mi | fá | sol | lá | si | dó | |||||||
| 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 | |||||||
| V | V | V | V | V | V | V | ||||||||
| 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 |
Percebemos que a dominante é o quinto grau da escala. Uma quinta acima do dó está o sol; uma quinta acima do sol está o ré; uma quinta acima do ré está o lá; assim, seguindo o ciclo das quintas, obtemos todas as notas da escala diatônica e retornamos ao dó.
Para sabermos em que ponto da corda dó o instrumentista deve pôr o dedo para obter as notas sucessivas da escala diatônica, basta olharmos a figura abaixo:

Intervalos[editar | editar código-fonte]
O intervalo entre duas notas é definido da seguinte maneira: se a frequência de uma nota é , e a da outra é , então o intervalo entre elas é a razão . Se esta razão for igual a 2, o intervalo é chamado de oitava justa. Outros intervalos também recebem nomes especiais: = quinta justa, = quarta justa, = terça maior, = terça menor, = tom maior, = tom menor, = semitom. O intervalo entre o tom maior e o tom menor, igual a 81/80, é chamado uma coma pitagórica, e é considerado o menor intervalo perceptível pelo ouvido humano.
Formação das escalas maiores[editar | editar código-fonte]
A escala que acabamos de obter também se chama a escala de dó maior. Se tivéssemos começado com a corda sol de um instrumento musical, e fizéssemos a mesmíssima divisão da corda que fizemos acima, obteríamos não mais a escala de dó maior, mas sim a escala de sol maior. A escala que criamos acima tem a seguinte distribuição de intervalos:
| dó | ré | mi | fá | sol | lá | si | dó | |||||||
| V | V | V | V | V | V | V | ||||||||
| tom | tom | semitom | tom | tom | tom | semitom |
Suponhamos que queiramos formar uma escala que soe melodicamente igual à escala de dó maior, mas começando na nota sol.
| sol | lá | si | dó | ré | mi | fá | sol | |||||||
| V | V | V | V | V | V | V | ||||||||
| tom | tom | semitom | tom | tom | semitom | tom |
A escala acima não soa melodicamente igual à escala de dó maior, e é fácil ver porque. A distribuição dos semitons não é a mesma. Para que isto aconteça, uma nota da escala tem que ser alterada. Mais precisamente, o fá tem que subir um pouco para ficar mais próximo do sol e mais longe do mi. Ou seja: dizemos que o fá tem que virar fá sustenido. Resolvendo uma equação, acharemos facilmente que precisamos multiplicar a frequência desta nota por 25/24 (dividindo o intervalo da terça maior pelo intervalo da terça menor).
Definição: Sustenir uma nota é multiplicar sua frequência por 25/24.
Similarmente, se quisermos criar uma outra escala que soe melodicamente igual à escala de dó maior, mas começando na nota fá, veremos que teremos que alterar uma nota da escala. Mais precisamente, o si vai ter que virar si bemol.
Definição: Bemolizar uma nota é multiplicar sua frequência por 24/25.
Ver também[editar | editar código-fonte]
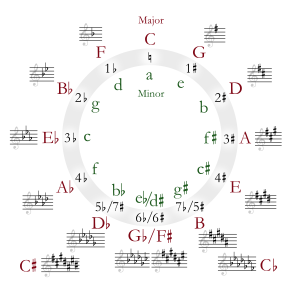 |
| |||||||||||||||||||||||||||||||||||||||||||||||||
| A tabela indica o número de sustenidos ou bemóis de cada escala. As escalas menores estão escritas em minúsculas. | ||||||||||||||||||||||||||||||||||||||||||||||||||






















