Sistema de numeração duodecimal
Origem: Wikipédia, a enciclopédia livre.
| Sistemas de numeração por cultura | |
|---|---|
| Numerais hindu-arábico | |
| Árabe ocidental Árabe oriental Família indiana |
Khmer Mongólico Thai |
| Numerais leste-asiáticos | |
| Chinês Counting rods Japonês |
Coreano Suzhou |
| Numerais alfabéticos | |
| Abjad Armênio Āryabhaṭa Cirílica |
Ge'ez Grego (jônio) Hebraico |
| Outros sistemas | |
| Ático Babilônica Brahmi Egípcios Etrusco |
Inuíte Maia Romano Urnfield |
| Lista de sistemas de numeração | |
| Sistema de numeração posicional | |
| 5, 10, 15, 20 | |
| 2, 4, 8, 16, 32, 64 | |
| 3, 6, 9, 12, 24, 30, 36, 60 | |
| 1, 7, 13, 26 | |
O sistema de numeração duodecimal (também conhecido como base-12) é um sistema de numeração que usa o número 12 como sua base.
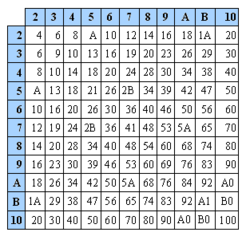
O número 12 possui seis fatores, que são 1, 2, 3, 4, 6 e 12.
