Lei de Bragg

Em física do estado sólido, a Lei de Bragg está relacionada ao espalhamento de ondas quando incidentes em um cristal e sugere uma explicação para os efeitos difrativos observados por esta interação. Estes padrões são explicados relacionando os vetores de onda do feixe incidente e espalhado em uma rede cristalina para o caso de seu espalhamento elástico com os átomos do material. No caso de ondas de raios X, ao atingirem um átomo, o campo elétrico da radiação provoca uma força na nuvem eletrônica acelerando as cargas livres do material (elétrons). O movimento das mesmas re-irradia ondas de aproximadamente mesma frequência (o espalhamento não é totalmente elástico, podendo haver interações de criação e aniquilação de fônons, porém em uma escala de energia muito menor). Nesse modelo, as frequências incidente e espalhada são consideradas idênticas. As ondas emergentes interferem entre si construtiva e destrutivamente, gerando padrões de difração no espaço que podem ser medidos em um filme ou detector. O padrão de difração resultante é a base da análise difrativa, chamada difração de Bragg.

A difração de Bragg (também chamada de formulação de Bragg da difração de raios X) foi proposta originalmente por William Lawrence Bragg e William Henry Bragg em 1913, em resposta à descoberta de que sólidos cristalinos produziam padrões intrigantes de reflexão de raios x (ao contrário, por exemplo, de um líquido). Eles descobriram que esses cristais, para alguns comprimentos de onda e ângulos de incidência específicos, produziam intensos picos de radiação refletida (conhecidos como picos de Bragg). O conceito de difração de Bragg se aplica igualmente a processos de difração de nêutrons e de elétrons. Ambos nêutrons e raios X possuem comprimento de onda compatível com as distâncias interatômicas (~150pm) e, portanto, constituem uma excelente ferramenta para se explorar essa ordem de grandeza de extensão.

W.L. Bragg explicou esse resultado empírico modelando o cristal como um conjunto de planos discretos, paralelos e separados por uma distância constante d, propondo que a radiação incidente produziria um pico de Bragg se as reflexões especulares de vários planos interferissem construtivamente, ou seja, se a diferença de fase entre as frentes de onda refletidas por planos consecutivos fosse de $2\pi$ radianos.

A lei de Bragg foi derivada pelo físico Sir William Lawrence Bragg. em 1912 e apresentada pela primeira vez em 11 de Novembro de 1912 à Sociedade Filosófica de Cambridge. Embora simples, a lei de Bragg confirmou a existência de partículas reais na escala atômica, e forneceu uma nova e poderosa ferramenta para o estudo de cristais utilizando difração de raios X e nêutrons. William Lawrence Bragg e seu pai, Sir William Henry Bragg, foram laureados com o Prêmio Nobel de física em 1915 por seu trabalho em determinar estruturas cristalinas, a começar pelo NaCl, ZnS e diamante. Eles são a única equipe formada por pai e filho a ganhar o prêmio conjuntamente. W.L. Bragg tinha 25 anos de idade, o que faz dele o mais jovem laureado pela academia Sueca.

Condição de Bragg

A periodicidade do cristal faz com que haja planos de átomos separados por uma distância fixa nas diferentes direções do espaço. A difração de Bragg ocorre quando a radiação eletromagnética ou ondas de matéria de comprimento de onda comparável à distância entre dois planos de átomos é refletida especularmente por planos consecutivos. Nota-se que partículas em movimento, incluindo elétrons, prótons e nêutrons têm um comprimento de onda associado de de Broglie:

$\lambda ={\frac {h}{p}}$ ,

onde $p$ é o momento da partícula.

Modelo de Bragg em duas dimensões: A diferença de caminho óptico entre os dois raios é $2d\sin \theta$, onde $d$ é a distância entre os planos considerados e $\theta$, o ângulo de incidência.

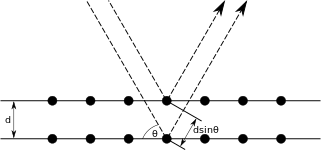
A próxima equação é conhecida como Lei de Bragg. Para termos uma diferença de fase entre dois raios igual a $2\pi$ radianos, é necessária a condição

$2d\sin \theta =n\lambda \;,\;\!$

onde $n$ é um inteiro, $\lambda$ é o comprimento de onda da radiação incidente, $d$ é a distância entre planos atômicos e $\theta$ é o ângulo de incidência em relação ao plano considerado. Dessa maneira, existe uma dependência entre o ângulo de incidência e a intensidade refletida. Como cada plano reflete de $10^{-3}$ a $10^{-5}$ do total da radiação incidente, temos de $10^{3}$ a $10^{5}$ planos contribuindo para a reflexão total. Se os raios refletidos estão fora de fase, a soma das muitas contribuições(reflexões por planos diferentes) tenderá a zero, de maneira que podemos observar picos localizados nos ângulos onde condição de Bragg é satisfeita.

Densidade eletrônica

Análise de Fourier

Para entendermos melhor o comportamento da onda espalhada, vamos considerar como modelo um cristal perfeito, formado por uma célula primitiva que se repete no espaço. A descrição matemática do cristal é invariante sob uma translação espacial

${\vec {T}}=u_{1}{\vec {a}}_{1}+u_{2}{\vec {a}}_{2}+u_{3}{\vec {a}}_{3}$

onde os $u_{i}$ são números inteiros e os vetores ${\vec {a}}_{i}$ são os vetores associados aos eixos do cristal, cujas magnitudes $a_{i}$ são as distâncias entre sítios (pontuais) da rede nas direções ${\hat {a}}_{i}$. Todas as propriedades locais do cristal, como densidade de momento magnético, concentração de carga ou densidade eletrônica, serão invariantes sob uma translação da forma ${\vec {T}}$ para qualquer combinação de $u_{i}$

$F({\vec {r}}+{\vec {T}})=F({\vec {r}})$ .

Essa periodicidade permite que realizemos uma expansão da densidade eletrônica $n({\vec {r}})$ em série de Fourier. Considerando primeiro apenas uma componente dimensional, temos:

$n(x)=\sum _{p>0}^{}[C_{p}\cos {\frac {2\pi px}{a_{1}}}+S_{p}\sin {\frac {2\pi px}{a_{1}}}]$,

onde $C_{p}$ e $S_{p}$ são constantes reais e $a_{1}=|{\vec {a}}_{1}|$. É imediato que

$n(x+a_{1})=n(x)\;\!$ .

Um ponto ${\frac {2\pi p}{a_{1}}}$ é um ponto no chamado espaço recíproco do cristal. Os coeficientes da expansão serão tais que apenas os termos que condizem com a periodicidade do cristal no espaço real (das posições) poderão ser diferentes de zero.

É conveniente escrever a soma como uma exponencial complexa através da relação de Euler:

$e^{ix}=\cos x+i\sin x\;\!$

Com essa notação, podemos escrever a expansão como

$n(x)=\sum _{p=-\infty }^{\infty }[n_{p}e^{\frac {i2\pi px}{a_{1}}}]$ ,

onde o somatório percorre todos os valores inteiros de p. O termo $n_{p}$ agora é, em geral, um número complexo, portanto precisamos de uma condição que faça com que $n(x)$ seja uma função real como tínhamos originalmente. A condição

$n_{p}=n^{*}\!_{-p}$

faz com que

$[n_{p}e^{\frac {i2\pi px}{a_{1}}}+n_{-p}e^{\frac {-i2\pi px}{a_{1}}}]=2Re[n_{p}]\cos {\frac {i2\pi px}{a_{1}}}-2Im[n_{p}]\sin {\frac {i2\pi px}{a_{1}}}$ ,

que é uma função real.

Estender o argumento para três dimensões é algo direto:

$n({\vec {r}})=\sum _{G}^{}n_{p}e^{{\vec {G}}\cdot {\vec {r}}}$ .

O somatório triplo foi omitido para preservar a clareza da expressão, mas é importante lembrar que a soma é realizada sobre todos as combinações possíveis de $v_{1},v_{2},v_{3}\;\!$ (definido na próxima subseção). Assim, precisamos encontrar um conjunto de vetores ${\vec {G}}$ que satisfaçam a relação de invariância por translação ${\vec {T}}$.

Tendo a expressão para a expansão de Fourier para densidade eletrônica, podemos obter os coeficientes da expansão em uma dimensão através de

$n_{p}=a_{1}^{-1}\int _{0}^{a_{1}}n(x)e^{\frac {-i2\pi px}{a_{1}}}\,dx$

Substituindo a expressão expandida para $n(x)$ na integral acima, temos

$n_{p}=a_{1}^{-1}\sum _{p'}^{}n_{p'}\int _{0}^{a_{1}}e^{\frac {i2\pi (p-p')x}{a_{1}}}\,dx$

O caso $p\neq p'$ faz com que o valor da integral seja

${\frac {a_{1}}{i2\pi (p'-p)}}(e^{i2\pi (p'-p)}-1)=0$ ,

pois $p'-p$ é um inteiro e $e^{i2\pi (inteiro)}=1$. No caso $p'=p$, temos $e^{0}=1$, de maneira que o valor da integral é $a_{1}$ e $n_{p}={\frac {a_{1}n_{p}}{a_{1}}}=n_{p}$. De maneira semelhante, podemos inverter o caso tridimensional, obtendo

$n_{G}=V_{c}^{-1}\int _{}^{}\int _{}^{}\int _{}^{}n({\vec {r}})e^{(-i{\vec {G}}\cdot {\vec {r}})}dV$

onde a integração é realizada sobre uma célula primitiva e $V_{c}$ é o volume da mesma.

Rede Recíproca

Podemos construir, a partir dos vetores da base ${\vec {a}}_{1},{\vec {a}}_{2},{\vec {a}}_{2}$, a base da rede recíproca

${\vec {b}}_{1}=2\pi {\frac {a_{2}\times a_{3}}{a_{1}\cdot a_{2}\times a_{3}}}$

${\vec {b}}_{2}=2\pi {\frac {a_{3}\times a_{1}}{a_{1}\cdot a_{2}\times a_{3}}}$

${\vec {b}}_{3}=2\pi {\frac {a_{1}\times a_{2}}{a_{1}\cdot a_{2}\times a_{3}}}$

ou de forma condensada, utilizando o tensor ou símbolo de Levi-Civita,

${\vec {b}}_{i}=2\pi {\frac {a_{j}\times a_{k}}{|a_{i}\cdot a_{j}\times a_{k}|}}\varepsilon _{ijk}.$

Por análise vetorial simples temos

${\vec {b}}_{i}\cdot {\vec {a}}_{j}=2\pi \delta _{ij},$

onde $\delta _{ij}$ é o delta de Kronecker.

Definimos ${\vec {G}}$ como sendo um vetor da forma

${\vec {G}}=v_{1}{\vec {b}}_{1}+v_{2}{\vec {b}}_{2}+v_{3}{\vec {b}}_{3}$ ,

onde os $v_{i}\;\!$ são números inteiros e os ${\vec {b}}_{i}$ são a base da rede recíproca. Estamos agora em condições de descrever a periodicidade de $n({\vec {r}})$ combinando a definição de ${\vec {G}}$ e a expansão em coeficientes de Fourier de $n({\vec {r}})$:

$n({\vec {r}})=\sum _{\vec {G}}^{}n_{p}e^{{\vec {G}}\cdot {\vec {r}}}$

$n({\vec {r}}+{\vec {T}})=\sum _{\vec {G}}^{}n_{p}e^{{\vec {G}}\cdot {\vec {r}}}e^{{\vec {G}}\cdot {\vec {T}}}$

O termo à direita pode ser escrito como

$e^{{\vec {G}}\cdot {\vec {T}}}=e^{i(v_{1}{\vec {b}}_{1}+v_{2}{\vec {b}}_{2}+v_{3}{\vec {b}}_{3})\cdot (u_{1}{\vec {a}}_{1}+u_{2}{\vec {a}}_{2}+u_{3})}=e^{i2\pi (v_{1}u_{1}+v_{2}u_{2}+v_{3}u_{3})}$

e como todos os $u_{i},v_{i}$ são inteiros e a exponencial de $2i\pi$ vezes um número inteiro é um, obtemos o resultado desejado, isto é, a invariância da densidade eletrônica, pois

$n({\vec {r}}+{\vec {T}})=\sum _{\vec {G}}^{}n_{p}e^{{\vec {G}}\cdot {\vec {r}}}e^{{\vec {G}}\cdot {\vec {T}}}=\sum _{\vec {G}}^{}n_{p}e^{{\vec {G}}\cdot {\vec {r}}}1=\sum _{\vec {G}}^{}n_{p}e^{{\vec {G}}\cdot {\vec {r}}}=n({\vec {r}})$ .

Amplitude de Espalhamento

Definimos a amplitude de espalhamento como sendo uma função que depende da densidade eletrônica e dos vetores de ondas incidente e refletido ${\vec {k}}$ e ${\vec {k}}'$, a princípio ondas planas monocromáticas:

$F=\int _{}^{}\int _{}^{}\int _{}^{}n({\vec {r}})e^{i({\vec {k}}-{\vec {k}}')\cdot {\vec {r}}}dV$ .

As integrais são realizadas sobre o volume do cristal inteiro. Embora tenhamos considerado um modelo onde o cristal é perfeito e infinito, uma amostra macroscópica é aproximadamente infinita se comparadas as suas dimensões com as distâncias interatômicas de uma rede cristalina, da ordem de $10^{-10}$ metros. O vetor de onda incidente tem a mesma energia que o vetor difratado, conforme a condição de espalhamento elástico considerando a rede cristalina como muito massiva e imóvel. A condição de conservação de energia é

$|{\vec {k}}|=|{\vec {k}}'|$ .

Definimos o vetor de espalhamento como sendo

$\Delta {\vec {k}}={\vec {k}}'-{\vec {k}}$ ,

de maneira que a expressão anterior se torna

$F=\int _{}^{}\int _{}^{}\int _{}^{}n({\vec {r}})e^{-i\Delta {\vec {k}}\cdot {\vec {r}}}dV$.

Introduzimos agora a expansão em série de Fourier para $n({\vec {r}})$ nessa expressão para obter

$F=\sum _{G}^{}\int _{}^{}\int _{}^{}\int _{}^{}n_{G}e^{i({\vec {G}}-\Delta {\vec {k}})\cdot {\vec {r}}}dV$ .

Quando o vetor de espalhamento é igual a algum vetor da rede recíproca, isto é,

$\Delta {\vec {k}}={\vec {G}}$ ,

a exponencial é nula e

$F=Vn_{G}$.

Quando o vetor de espalhamento difere significantemente de qualquer vetor da rede recíproca, o grande número de oscilações da exponencial devido à variação de ${\vec {r}}$ dentro da integral faz com que $F$ rapidamente tenda a zero.

Podemos reescrever a relação entre os vetores de onda e os vetores da base recíproca utilizando a definição do vetor de espalhamento

${\vec {k}}+{\vec {G}}={\vec {k}}'$ .

Pela conservação da energia, obtivemos que as magnitudes dos vetores ${\vec {k}}$ devem ser iguais. Portanto, tomando o produto escalar dos dois lados:

$({\vec {k}}+{\vec {G}})\cdot ({\vec {k}}+{\vec {G}})={\vec {k}}'\cdot {\vec {k}}'=k'^{2}=k^{2}$

Portanto,

$({\vec {k}}+{\vec {G}})^{2}=k^{2}$.

ou ainda

$2{\vec {k}}\cdot {\vec {G}}+G^{2}=0$ .

Pelas definições de rede recíproca, é possível mostrar que, se ${\vec {G}}$ é um vetor da rede recíproca, então $-{\vec {G}}$ também é. Isso faz com que seja possível escrever a condição acima como

$2{\vec {k}}\cdot {\vec {G}}=G^{2}$ .

As últimas duas equações são formulações equivalentes da condição de difração de Bragg. O espaçamento $d(hkl)$ entre planos cristalinos paralelos entre si, normais à direção

${\vec {G}}=h{\vec {b}}_{1}+k{\vec {b}}_{2}+l{\vec {b}}_{3}$ ,

onde h, k, l são inteiros, é dado por

$d(hkl)={\frac {2\pi }{|{\vec {G}}|}}$ .

Combinando a definição de $|{\vec {k}}|$,

$|{\vec {k}}|={\frac {2\pi }{\lambda }}$

onde $\lambda$ é o comprimento de onda incidente, com a definição de produto escalar e do módulo de ${\vec {G}}$, temos:

$2\left({\frac {2\pi }{\lambda }}{\frac {2\pi }{d(hkl)}}\right)\cos \phi =\left({\frac {2\pi }{d(hkl)}}\right)^{2}$ ,

sendo $\phi$ o ângulo entre os vetores ${\vec {k}}$ e $-{\vec {G}}$ .

Conforme observamos acima, o vetor ${\vec {G}}$ é normal ao plano $d(hkl)$. Logo, o vetor $-{\vec {G}}$ também é normal ao plano e o ângulo entre esse vetor e um vetor no plano considerado é $-{\frac {\pi }{2}}$. O menor ângulo formado entre o vetor de onda incidente ${\vec {k}}$ e o plano é, por análise geométrica, igual a

Modelo de Bragg em duas dimensões: Relação entre os ângulos de incidência e de espalhamento tomando como referência o plano cristalino e a vetor $-{\vec {G}}$ para obtenção da formulação usual da lei de Bragg. Pela condição de reflexão especular, é possível deduzir que o ângulo entre os vetores de onda incidente e refletido é de $2\theta$

$-{\frac {\pi }{2}}+\phi =-\theta$

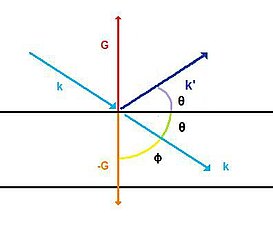
ou rearranjando os fatores:

$\phi ={\frac {\pi }{2}}-\theta$ .

Podemos reescrever a condição de Bragg utilizando o ângulo entre o vetor incidente e o plano, ao invés de considerar o ângulo entre o vetor incidente e o vetor $-{\vec {G}}$, utilizando a relação

$\cos \phi =\cos {\left({\frac {\pi }{2}}-\theta \right)}=\sin \theta$

Assim, recuperamos o resultado obtido pela análise geométrica simples, escrito à maneira usual da formulação da lei de Bragg:

$2d(hkl)\sin \theta =\lambda \;\!$ .

Aqui, $\theta$ é o ângulo entre o vetor de onda e o plano cristalino descrito pelos inteiros h, k e l. Existe uma diferença entre essa equação e a primeira equação apresentada aqui como condição de difração, a saber, a multiplicação do lado direito da equação por um número inteiro. Isso se dá pelo fato dos índices de Miller poderem conter um fator comum n, que é eliminado no processo de obtenção dos mesmos. Fisicamente, isso significa que a expressão

$2\sin \theta d(hkl)=n\lambda \;\!$

dá a condição de difração de Bragg para um plano de índices de Miller $({\frac {h}{n}}\;{\frac {k}{n}}\;{\frac {l}{n}})$.