Problema de Monty Hall

Em busca de um novo carro, o jogador escolhe a porta 1. O apresentador então abre a porta 3 revelando que ela não tem o carro, e oferece ao jogador a possibilidade de escolher a porta 2 ao invés da porta 1.

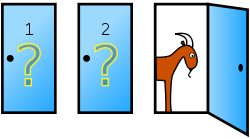
O problema de Monty Hall, tambem conhecido por paradoxo de Monty Hall ou problema do Silvio Santos é um problema matemático e paradoxo que surgiu a partir de um concurso televisivo dos Estados Unidos chamado Let’s Make a Deal, exibido na década de 1970.

O jogo consiste no seguinte: Monty Hall (o apresentador) apresentava 3 portas aos concorrentes, sabendo que atrás de uma delas está um carro (prémio bom) e que as outras têm prêmios de pouco valor.

1. Na 1ª etapa o concorrente escolhe uma porta (que ainda não é aberta);
2. De seguida Monty abre uma das outras duas portas que o concorrente não escolheu, sabendo à partida que o carro não se encontra aí;
3. Agora com duas portas apenas para escolher — pois uma delas já se viu, na 2ª etapa, que não tinha o prêmio — e sabendo que o carro está atrás de uma delas, o concorrente tem que se decidir se permanece com a porta que escolheu no início do jogo e abre-a ou se muda para a outra porta que ainda está fechada para então a abrir.

Qual é a estratégia mais lógica? Ficar com a porta escolhida inicialmente ou mudar de porta? Com qual das duas portas ainda fechadas o concorrente tem mais probabilidades de ganhar? Por quê?

Realmente não é assim tão indiferente mudar ou ficar na mesma porta. No início, quando se escolheu uma das portas, havia 1/3 de probabilidade de ganhar o carro. Não existe razão nenhuma para essa probabilidade mudar após o Monty Hall ter aberto uma das portas que não era premiada. As outras duas portas não escolhidas tinham em conjunto 2/3 de probabilidade de ocultarem o carro, e quando uma dessa portas é aberta (por não ter prêmio) a porta não escolhida que continua fechada passa a ter 2/3 de probabilidade de ser a porta do carro.

A confusão é feita seguindo o raciocínio que parece mais lógico: "mas a porta escolhida também continua fechada... então cada uma das portas fechadas passa a ter 1/2 de chance de ter o carro".

O problema

Este pequeno problema é muito mais difícil do que parece, e tornou-se famoso nos EUA como o problema de Monty Hall, devido ao apresentador que possuía um quadro bem similar (ou o contrário seria mais apropriado) em seu programa popular 'Let's Make a Deal' ['Vamos fazer um trato'] nos anos 70, algo como os diversos programas de auditório que ficaram famosos no Brasil com o apresentador Silvio Santos.

A resposta intuitiva, porém errada

A resposta intuitiva ao problema é a de que quando o apresentador revelou uma porta não-premiada, o concorrente teria à frente um novo dilema com apenas duas portas e um prêmio, portanto as chances de que o prêmio esteja em qualquer uma das duas portas seriam de 50%. O apresentador teria nos ajudado, já que nossas chances subiram de 1/3 para 1/2, mas realmente não faria diferença trocar ou não de porta uma vez que ambas teriam as mesmas chances de possuírem o prêmio. No entanto, esta resposta está errada, pois a porta que o apresentador abre depende da porta que o concorrente escolher inicialmente. O apresentador sabe desde o começo onde está o prêmio (ele nunca abrirá uma porta premiada). Ao abrir uma porta, ele não está criando um jogo todo novo, mas está dando informações valiosas sobre o jogo original. É por isso que a resposta é tão contra-intuitiva: parece-nos que o apresentador abriu uma porta aleatoriamente, mas isso está muito longe da verdade. Como se observa, se o concorrente tiver escolhido inicialmente uma porta não-premiada (isto é, com o prémio mau), o apresentador não tem liberdade de escolha e só pode abrir uma porta.

A solução

A resposta correta e contra-intuitiva é que é vantajoso trocar. Na verdade é duas vezes mais provável ganhar o prêmio se se trocar de porta do que se não o fizer.

Existem três portas - A, B e C. Quando o concorrente escolheu uma delas, digamos a A, a chance de que ela seja a premiada é de 1/3. Como conseqüência, a probabilidade de que tenha errado, ou em outras palavras, de que o prêmio esteja nas outras duas portas B ou C é de 2/3. Pode-se comprovar isso somando a probabilidade de cada uma das outras portas ou simplesmente sabendo que a probabilidade de que haja um prêmio é sempre 1. O importante é ter em mente que a chance de o prêmio estar nas outras portas que você não escolheu é de 2/3.

Entendendo isso, basta ver que o apresentador abrirá sem erro uma dessas outras duas portas que contém um prémio mau, digamos que seja a B. Ao fazer isso, ele está lhe dando uma informação valiosa: se o prêmio estava nas outras portas que não escolheu (B ou C), então agora ele só pode estar na porta que você não escolheu e não foi aberta, ou seja, a porta C. Ou seja, se o concorrente errou ao escolher uma porta - e as chances disto são de 2/3 - então ao abrir uma das outras portas não-premiadas o apresentador está lhe dizendo onde está o prêmio. Toda vez que o concorrente tiver escolhido inicialmente uma porta errada, ao trocar de porta irá com certeza ganhar. Como as chances de que tenha errado em sua escolha inicial são de 2/3, se trocar suas chances de ganhar serão de 2/3 - e por conseguinte a chance de que ganhe se não trocar de porta é de apenas 1/3. É assim mais vantajoso trocar de porta.

A análise pode ser ilustrada em termos da chances de probabilidades iguais que o jogador inicialmente escolheu o carro, bode A, ou bode B (Economist 1999):

1. Apresentador revela um dos bodes Jogador escolhe carro (probabilidade 1/3) Trocar perde. 2. Apresentador tem que revelar Bode B Jogador escolhe Bode A (probabilidade 1/3) Trocar ganha. 3. Apresentador tem que revelar Bode A Jogador escolhe Bode B (probabilidade 1/3) Trocar ganha.

O jogador tem uma chance igual de inicialmente selecionar o carro, Bode A, ou Bode B. A troca resulta em uma vitória 2/3 das vezes.

O problema de Monty Hall é exposto em muitos cursos de probabilidades e de estatística, e um exercício com ele seria dado em Harvard e Princeton. Ele demonstra muito bem como nosso cérebro não foi feito para lidar intuitivamente com tais tipos específicos de problemas. Felizmente pode-se resolver o problema de Monty Hall no papel de forma simples e sem erro usando o teorema de Bayes relativo às probabilidades condicionadas.

Simulação em computador

Um programa de computador pode ser usado para demonstrar como a troca de porta em geral é mais vantajosa. O programa simula vários jogos, onde o jogador sempre estará trocando de porta. Em cada jogo é gerada uma escolha aleatória para o jogador, sendo que o carro sempre estará na primeira porta. Uma das portas é então aberta, e o jogador realiza a troca. As vitórias são computadas toda vez que a troca resultar na porta que contém o carro.

Usando boa aleatoriedade e executando o jogo um considerável número de vezes, podemos verificar que a taxa de acerto fica em torno de 2/3 ou 66%.

Ruby

O seguinte código-fonte em Ruby é um exemplo de programa que implementa esta simulação:

car = wins = 0
many = 1000000
 
many.times do |game| 
    choice1 = rand(3)
    host_opts = [0, 1, 2] - [choice1, car]
    choice2 = [0, 1, 2] - [choice1, host_opts.first]
    wins += 1 if choice2 == [car] 
 
    progress = ((game + 1) * 100) / many
    print("\b\b\b#{progress}%")
end
 
puts "\b\b\b\b#{wins} wins in #{many} games."
puts "Success rate of #{(wins * 100) / many}%"

Exemplo de saída (traduzido para português):

666840 vitórias em 1000000 jogos.
Taxa de sucesso em 67%.

ActionScript 3.0

O seguinte código-fonte em ActionScript 3.0 é um exemplo de programa que implementa esta simulação:

var cabra:uint = 0;
var carro:uint = 1;
var escolhido:uint = 2;
var tentativas:uint = 1000000;
var vitorias:uint = 0;
for(var i:uint=0; i<tentativas; i++){
        var escolha1:uint = Math.floor(Math.random()*3);
        var portas:Array = [cabra, cabra, carro];
        portas[escolha1] = escolhido;
 
        if(escolha1 != 0){
                portas.splice(0, 1);
        } else {
                portas.splice(1, 1);
        }
 
        var escolha2:uint = (portas[0] == cabra ? escolhido : carro); //Mudando a escolha
        if(escolha2 == carro){
                vitorias++;
        }
 
        var progresso:Number = ((i + 1) * 100) / tentativas;
        trace("Progresso: " + progresso);
}
trace(vitorias + " vitórias em " + tentativas + " tentativas.");
trace("Sucesso em: " + (vitorias * 100) / tentativas + "% das vezes.");

Exemplo de saída

666634 vitórias em 1000000 tentativas.
Sucesso em: 66.6634% das vezes.

Python

O seguinte código-fonte em Python também exemplifica o paradoxo de Monty Hall:

#! This script can be used to test the Monty Hall paradox
#! Variable "car" selects the door that hides the car: 0, 1 or 2.
#! Variable "switch" can be 1 (switch doors) or 0 (doesn't switch doors).
#! Feel free to use and modify!
#! Date: 2011-10-22
#! Author: Felipe Nascimento Martins
#! Brazil
 
#! This script can be used to test the Monty Hall paradox
#! Variable "car" selects the door that hides the car: 0, 1 or 2.
#! Variable "switch" can be 1 (switch doors) or 0 (doesn't switch doors).
#! Feel free to use and modify!
#! Date: 2011-10-22
#! Author: Felipe Nascimento Martins
#! Brazil
#! Edited to Python 3.2 by Daniel Petri, Brazil
#! Date: 2012-05-09
#! Edited to Python 3.2 by Emanuel Vianna, Brazil
#! Change: use xrange instead of range once range expands the entire
#! array to memory instead of use a lazy approach, that is, returns
#! a generator that gives you the next element at each iteration.
#! Date: 2012-05-09
 
import random
switch = 1
car = 0
wins = 0
max = 10000.0
for count in xrange(1,int(max)):
        car = int(random.random()*3)
        player_list = [0, 1, 2]
        choice1 = int(random.random()*3)
        player_list.remove(choice1)
        if player_list[0]==car:
                host_not_open=car
        elif player_list[1]==car:
                host_not_open=car
        else:
                host_not_open=player_list[int(random.random()*2)]
        if switch == 1:
                if car==host_not_open:
                        wins=wins+1
        elif car!=host_not_open:
                wins=wins+1
print('Wins = ',wins)
print('Won ', (wins/max)*100,'% of the games.')

Bibliografia

• Edward R. Scheinerman. Matemática Discreta - Uma Introdução. 1 ed. Brasil: Cengage Learning, 2003. 532 p. ISBN 85-221-0291-0