Ângulo reto: diferenças entre revisões
Etiquetas: Edição via dispositivo móvel Edição feita através do sítio móvel |
Etiquetas: Inserção de predefinição obsoleta editor de código 2017 |
||
| Linha 1: | Linha 1: | ||
[[Image:Right angle.svg|thumb|134px|Um ângulo reto é igual a 90 graus.]] |
|||
{{mais-notas|data=Junho de 2011}} |
|||
[[Image:Perpendicular-coloured.svg|right|thumb|Um segmento de linha (AB) desenhado para formar ângulos retos com uma linha (CD).]] |
|||
[[Ficheiro:Right angle.svg|direita|thumb|120px|Ângulo reto]] |
|||
[[Ficheiro:Brasil_A-1b.svg|alt=|miniaturadaimagem|120x120px|Uma Placa de Sinalização a dizer uma curva a direita, a seta da imagem é um '''ângulo reto''' ]] |
|||
'''Ângulo reto''' aquele que obrigatoriamente tem a característica de 90°(graus) e também é um [[ângulo]] formado quando uma semirreta, tocando em um ponto de uma outra [[reta]], cria dois ângulos iguais e perpendiculares.<ref name="euclides">[[Euclides]], ''Os Elementos'', ''Livro I'', ''Definição 10'' [http://aleph0.clarku.edu/~djoyce/java/elements/bookI/defI10.html <nowiki>[em linha]</nowiki>]</ref> |
|||
Na [[geometria]] e [[trigonometria]], um '''ângulo reto''' é um [[ângulo]] de exatamente 90° ([[Grau (geometria)|graus]]),<ref>{{cite web|title=Right Angle|url=http://www.mathopenref.com/angleright.html|website=Math Open Reference|accessdate=26 April 2017}}</ref> correspondendo a um quarto de [[Volta (geometria)|volta]].<ref>Wentworth p. 11</ref> Se um [[Raio (geometria)|raio]] é colocado de modo que seu ponto final esteja em uma linha e os ângulos adjacentes sejam iguais, então eles são ângulos retos.<ref>Wentworth p. 8</ref> O termo é um [[calque]] do [[latim]] ''angulus rectus''; aqui, reto significa "[[vertical]]", referindo-se à vertical perpendicular a uma linha de base horizontal. |
|||
É o ângulo formado por duas [[reta]]s [[perpendicular]]es. O ângulo reto corresponde ao ângulo com "quantidade de rotação" de 1/4 de círculo, dessa forma, dois ângulos retos formam um [[ângulo plano]]. |
|||
Conceitos geométricos intimamente relacionados e importantes são [[Perpendicularidade|retas perpendiculares]], que significam retas que formam ângulos retos em seu ponto de intersecção, e [[Perpendicularidade|ortogonalidade]], que é a propriedade de formar ângulos retos, geralmente aplicados a [[Vetor (matemática)|vetores]]. A presença de um ângulo reto em um [[triângulo]] é o fator que define os [[Triângulo retângulo|triângulos retos]],<ref>Wentworth p. 40</ref> fazendo o ângulo direito básico à trigonometria. |
|||
| ⚫ | |||
== Na geometria elementar == |
|||
Um [[retângulo]] é um [[quadrilátero]] com quatro ângulos retos. Um [[quadrado]] tem quatro ângulos retos, além de lados de comprimento igual. |
|||
{{DEFAULTSORT:Angulo Reto}} |
|||
| ⚫ | |||
O [[Teorema de Pitágoras]] indica como determinar um lado quando um triângulo é um [[triângulo retângulo]]. |
|||
[[ca:Angle#Angles notables]] |
|||
== Símbolos == |
|||
[[Image:Rtriangle.svg|thumb|Triângulo retângulo, com o ângulo reto mostrado através de um pequeno quadrado.]] |
|||
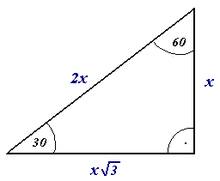
[[File:Triangle 30-60-90 rotated.png|thumb|Outra opção de indicar diagramaticamente um ângulo reto, usando uma curva angular e um pequeno ponto.]] |
|||
Em [[Unicode]], o símbolo para um ângulo reto é {{unichar|221f|Right angle|html=}}. Não deve ser confundido com o símbolo de forma semelhante {{unichar|231e|Bottom left corner|html=}}. Símbolos relacionados são {{unichar|22be|Right angle with arc|html=}}, {{unichar|299c|Right angle variant with square|html=}}, e {{unichar|299d|Measured right angle with dot|html=}}.<ref>Unicode 5.2 Character Code Charts [https://www.unicode.org/charts/PDF/U2200.pdf Mathematical Operators], [https://www.unicode.org/charts/PDF/U2980.pdf Miscellaneous Mathematical Symbols-B]</ref> |
|||
Nos [[Diagrama|diagramas]], o fato de um ângulo ser um ângulo reto geralmente é expresso pela adição de um pequeno ângulo reto que forma um quadrado com o ângulo no diagrama, como visto no diagrama de um triângulo retângulo à direita. O símbolo para um ângulo medido, um arco com um ponto, é usado em alguns países europeus, incluindo países de [[língua alemã]] e na [[Polónia|Polônia]], como um símbolo alternativo para um ângulo reto.<ref>{{cite book |last1=Müller-Philipp|first2=Hans-Joachim|last2=Gorski |first1=Susanne |year=2011 |title=Leitfaden Geometrie |trans-title=Handbook Geometry |url=https://books.google.com/books?id=PAdSPOBYHPUC |language=German |publisher=Springer |isbn=9783834886163}}</ref> |
|||
== Euclides == |
|||
Os ângulos retos são fundamentais nos [[Os Elementos|Elementos de Euclides]]. Eles são definidos no ''Livro 1, definição 10'', que também define retas perpendiculares. A ''definição 10'' não usa medições de graus numéricos, mas implica diretamente no que é um ângulo reto, ou seja, duas linhas retas que se interceptam para formar dois ângulos iguais e adjacentes.<ref>Heath p. 181</ref> As linhas retas que formam ângulos retos são chamadas perpendiculares.<ref>Heath p. 181</ref> Euclides usa ângulos retos nas ''definições 11 e 12'' para definir [[Ângulo agudo|ângulos agudos]] (aqueles menores que um ângulo reto) e [[Ângulo obtuso|ângulos obtusos]] (aqueles maiores que um ângulo reto).<ref>Heath p. 181</ref> Dois ângulos são chamados [[Ângulos complementares e suplementares|complementares]] se a soma deles for um ângulo reto.<ref>Wentworth p. 9</ref> |
|||
''Livro 1, Postulado 4'' afirma que todos os ângulos retos são iguais, o que permite que [[Euclides]] use um ângulo reto como uma unidade para medir outros ângulos. O comentador de Euclides, [[Proclo|Proclus]], deu uma prova desse postulado usando os postulados anteriores, mas pode-se argumentar que essa prova faz uso de algumas suposições ocultas. [[Giovanni Gerolamo Saccheri|Saccheri]] deu uma prova também, mas usando uma suposição mais explícita. Na [[Axiomas de Hilbert|axiomatização da geometria]] de [[David Hilbert|Hilbert]], essa afirmação é dada como um [[teorema]], mas somente depois de muito trabalho de base. Pode-se argumentar que, mesmo que o ''postulado 4'' possa ser comprovado a partir dos anteriores, na ordem em que Euclides apresenta seu material é necessário incluí-lo, pois sem ele o ''postulado 5'', que usa o ângulo reto como unidade de medida, não faz sentido.<ref>Heath pp. 200-201 for the paragraph</ref> |
|||
== Conversão para outras unidades == |
|||
Um ângulo reto pode ser expresso em diferentes unidades: |
|||
*<math>\frac{1}{4}</math> de [[Volta (geometria)|volta]] |
|||
* 90° ([[Grau (geometria)|graus]]) |
|||
*<math>\frac {\pi}{2}</math> [[Radiano|radianos]] |
|||
* 100 [[Grado (ângulo)|grado]] (também chamado de ''gradiano'' ou ''gon'') |
|||
* 8 pontos (de uma [[rosa dos ventos]] de 32 pontos) |
|||
* 6 horas ([[ângulo horário]] astronômico) |
|||
== Regra do 3-4-5 == |
|||
Ao longo da história, os carpinteiros e pedreiros conheceram uma maneira rápida de confirmar se um ângulo é um verdadeiro "ângulo reto". Baseia-se no [[Terno pitagórico|triplo pitagórico]] mais amplamente conhecido (3, 4, 5) e é chamado de "regra do 3-4-5". Do ângulo em questão, correndo uma linha reta ao longo de um lado com exatamente 3 unidades de comprimento, e ao longo do segundo lado exatamente 4 unidades de comprimento, criará uma [[hipotenusa]] (a linha mais longa oposta ao ângulo reto que conecta os dois pontos finais) exatamente 5 unidades de comprimento. Essa medição pode ser feita rapidamente e sem instrumentos técnicos. A lei geométrica por trás da medida é o [[teorema de Pitágoras]] ("O quadrado da hipotenusa de um triângulo retângulo é igual à soma dos quadrados dos dois lados adjacentes"). |
|||
== Teorema de Tales == |
|||
{{multiple image |
|||
| align = right |
|||
| image1 = 01-Rechter Winkel mittels Thaleskreis.gif |
|||
| width1 = 254 |
|||
| alt1 = |
|||
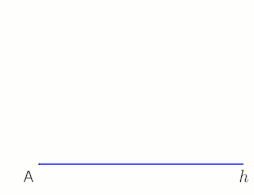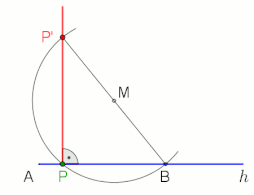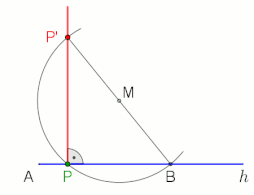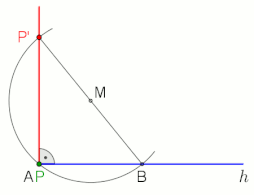
| caption1 = Construção da perpendicular à meia-linha h do ponto P (aplicável não só no ponto final A, M é livremente selecionável),<br>animação no final com pausa de 10 s |
|||
| image2 = 01-Rechter Winkel mittels Thaleskreis-II.gif |
|||
| width2 = 237 |
|||
| alt2 = |
|||
| caption2 = Construção alternativa se P fora da meia-linha h e a distância A a P' é pequena (B é livremente selecionável),<br> animação no final com pausa de 10 s |
|||
| footer = |
|||
}} |
|||
{{main|Teorema de Tales (círculo)}} |
|||
O teorema de [[Tales de Mileto|Tales]] afirma que um ângulo inscrito em um [[semicírculo]] (com um [[vértice]] no semicírculo e seus raios definidores passando pelos pontos finais do semicírculo) é um ângulo reto. |
|||
== Ver também == |
|||
{{Commons category|Right angles}} |
|||
*[[Sistema de coordenadas cartesiano|Sistema de coordenada cartesiana]] |
|||
*[[Perpendicularidade]] |
|||
*[[Retângulo]] |
|||
| ⚫ | |||
{{reflist}} |
|||
*{{cite book |title=A Text-Book of Geometry|first=G.A.|last=Wentworth |
|||
|publisher=Ginn & Co.|year=1895| |
|||
url=https://books.google.com/books?id=CyUAAAAAYAAJ#v=onepage&q&f=false}} |
|||
*Euclid, commentary and trans. by [[T. L. Heath]] ''Elements'' Vol. 1 (1908 Cambridge) [https://books.google.com/books?id=UhgPAAAAIAAJ Google Books] |
|||
| ⚫ | |||
Revisão das 22h54min de 8 de julho de 2019


Na geometria e trigonometria, um ângulo reto é um ângulo de exatamente 90° (graus),[1] correspondendo a um quarto de volta.[2] Se um raio é colocado de modo que seu ponto final esteja em uma linha e os ângulos adjacentes sejam iguais, então eles são ângulos retos.[3] O termo é um calque do latim angulus rectus; aqui, reto significa "vertical", referindo-se à vertical perpendicular a uma linha de base horizontal.
Conceitos geométricos intimamente relacionados e importantes são retas perpendiculares, que significam retas que formam ângulos retos em seu ponto de intersecção, e ortogonalidade, que é a propriedade de formar ângulos retos, geralmente aplicados a vetores. A presença de um ângulo reto em um triângulo é o fator que define os triângulos retos,[4] fazendo o ângulo direito básico à trigonometria.
Na geometria elementar
Um retângulo é um quadrilátero com quatro ângulos retos. Um quadrado tem quatro ângulos retos, além de lados de comprimento igual.
O Teorema de Pitágoras indica como determinar um lado quando um triângulo é um triângulo retângulo.
Símbolos

Em Unicode, o símbolo para um ângulo reto é U+221F ∟ RIGHT ANGLE (∟). Não deve ser confundido com o símbolo de forma semelhante U+231E ⌞ BOTTOM LEFT CORNER (⌞, ⌞). Símbolos relacionados são U+22BE ⊾ RIGHT ANGLE WITH ARC (⊾), U+299C ⦜ RIGHT ANGLE VARIANT WITH SQUARE (⦜), e U+299D ⦝ MEASURED RIGHT ANGLE WITH DOT (⦝).[5]
Nos diagramas, o fato de um ângulo ser um ângulo reto geralmente é expresso pela adição de um pequeno ângulo reto que forma um quadrado com o ângulo no diagrama, como visto no diagrama de um triângulo retângulo à direita. O símbolo para um ângulo medido, um arco com um ponto, é usado em alguns países europeus, incluindo países de língua alemã e na Polônia, como um símbolo alternativo para um ângulo reto.[6]
Euclides
Os ângulos retos são fundamentais nos Elementos de Euclides. Eles são definidos no Livro 1, definição 10, que também define retas perpendiculares. A definição 10 não usa medições de graus numéricos, mas implica diretamente no que é um ângulo reto, ou seja, duas linhas retas que se interceptam para formar dois ângulos iguais e adjacentes.[7] As linhas retas que formam ângulos retos são chamadas perpendiculares.[8] Euclides usa ângulos retos nas definições 11 e 12 para definir ângulos agudos (aqueles menores que um ângulo reto) e ângulos obtusos (aqueles maiores que um ângulo reto).[9] Dois ângulos são chamados complementares se a soma deles for um ângulo reto.[10]
Livro 1, Postulado 4 afirma que todos os ângulos retos são iguais, o que permite que Euclides use um ângulo reto como uma unidade para medir outros ângulos. O comentador de Euclides, Proclus, deu uma prova desse postulado usando os postulados anteriores, mas pode-se argumentar que essa prova faz uso de algumas suposições ocultas. Saccheri deu uma prova também, mas usando uma suposição mais explícita. Na axiomatização da geometria de Hilbert, essa afirmação é dada como um teorema, mas somente depois de muito trabalho de base. Pode-se argumentar que, mesmo que o postulado 4 possa ser comprovado a partir dos anteriores, na ordem em que Euclides apresenta seu material é necessário incluí-lo, pois sem ele o postulado 5, que usa o ângulo reto como unidade de medida, não faz sentido.[11]
Conversão para outras unidades
Um ângulo reto pode ser expresso em diferentes unidades:
- de volta
- 90° (graus)
- radianos
- 100 grado (também chamado de gradiano ou gon)
- 8 pontos (de uma rosa dos ventos de 32 pontos)
- 6 horas (ângulo horário astronômico)
Regra do 3-4-5
Ao longo da história, os carpinteiros e pedreiros conheceram uma maneira rápida de confirmar se um ângulo é um verdadeiro "ângulo reto". Baseia-se no triplo pitagórico mais amplamente conhecido (3, 4, 5) e é chamado de "regra do 3-4-5". Do ângulo em questão, correndo uma linha reta ao longo de um lado com exatamente 3 unidades de comprimento, e ao longo do segundo lado exatamente 4 unidades de comprimento, criará uma hipotenusa (a linha mais longa oposta ao ângulo reto que conecta os dois pontos finais) exatamente 5 unidades de comprimento. Essa medição pode ser feita rapidamente e sem instrumentos técnicos. A lei geométrica por trás da medida é o teorema de Pitágoras ("O quadrado da hipotenusa de um triângulo retângulo é igual à soma dos quadrados dos dois lados adjacentes").
Teorema de Tales
animação no final com pausa de 10 s
O teorema de Tales afirma que um ângulo inscrito em um semicírculo (com um vértice no semicírculo e seus raios definidores passando pelos pontos finais do semicírculo) é um ângulo reto.
Ver também
Referências
- ↑ «Right Angle». Math Open Reference. Consultado em 26 April 2017 Verifique data em:
|acessodata=(ajuda) - ↑ Wentworth p. 11
- ↑ Wentworth p. 8
- ↑ Wentworth p. 40
- ↑ Unicode 5.2 Character Code Charts Mathematical Operators, Miscellaneous Mathematical Symbols-B
- ↑ Müller-Philipp, Susanne; Gorski, Hans-Joachim (2011). Leitfaden Geometrie [Handbook Geometry] (em German). [S.l.]: Springer. ISBN 9783834886163
- ↑ Heath p. 181
- ↑ Heath p. 181
- ↑ Heath p. 181
- ↑ Wentworth p. 9
- ↑ Heath pp. 200-201 for the paragraph
- Wentworth, G.A. (1895). A Text-Book of Geometry. [S.l.]: Ginn & Co.
- Euclid, commentary and trans. by T. L. Heath Elements Vol. 1 (1908 Cambridge) Google Books