Filtro passa-baixo
Este artigo não cita fontes confiáveis. (Janeiro de 2016) |
Filtro passa-baixo é o nome comum dado a um circuito eletrônico que permite a passagem de baixas frequências sem dificuldades e atenua (ou reduz) a amplitude das frequências maiores que a frequência de corte. A quantidade de atenuação para cada frequência varia de acordo com as configurações adotadas no projeto do filtro.
O conceito de filtro passa-baixo existe de muitas formas diferentes, incluindo os circuitos eletrônicos, algoritmos digitais para trabalhar com conjuntos de dados, barreiras acústicas, trabalhos com imagens, entre outros.
Exemplos de filtros passa-baixo[editar | editar código-fonte]
Uma barreira sólida atua como um filtro passa-baixo para as ondas do som. Quando se está em um quarto e a música passa através de uma parede, as notas mais baixas (graves) são ouvidas com mais facilidade do que as notas mais altas (agudas), que são largamente filtradas. Similarmente, uma música muito alta ouvida em um carro é ouvida apenas como alguns ruídos pelos ocupantes dos outros veículos, pois os veículos fechados (e a barreira de ar) atuam como um filtro passa-baixo muito seletivo, atenuando os tons mais agudos.
Os filtros passa-baixo eletrônicos são utilizados para controlar subwoofers e outros tipos de alto-falantes, para bloquear os picos mais agudos que não seriam transmitidos eficientemente.
Os transmissores de rádio utilizam filtros passa-baixo para filtrar as emissões harmônicas que podem causar interferência com outras comunicações.
O DSL splitters utilizam filtros passa-baixo e passa-alto para separar os sinais de DSL e o POTS compartilhando o mesmo par de fios.
Os filtros passa-baixo também possuem um papel importante no trabalho dos sons em música eletrônica quando esta é criada por sintetizadores analógicos, como o TB-303, criado pela Roland Corporation.
Filtros reais e ideais[editar | editar código-fonte]
Um filtro passa-baixo ideal elimina completamente todas as frequências acima da frequência de corte, enquanto permite que as frequências abaixo desta faixa passem inalteradas. A região de transição nos filtros práticos não existe. Um filtro passa baixas ideal pode ser obtido matematicamente (teoricamente) multiplicando o sinal pela função retangular no domínio da frequência ou fazendo a convolução com uma função de sincronização no domínio do tempo.
Entretanto, este filtro não existe para sinais reais, pois a função de sincronização destes estende-se ao infinito. O filtro teria que prever o futuro e ter conhecimento infinito do passado para realizar a convolução. Isto é efetivamente realizado para sinais digitais pré-gravados, ou perfeitamente cíclicos, que se repetem infinitamente.
Os filtros reais para as aplicações em tempo real aproximam-se do filtro ideal por atrasarem o sinal por um período de tempo, permitindo uma pequena "visão" do futuro. Isto é manifestado como a mudança de fase. Uma maior precisão na aproximação requer um atraso maior.
O teorema de amostras de Nyquist-Shannon descreve como utilizar um filtro passa-baixo perfeito e a fórmula de interpolação de Nyquist-Shannon mostra como reconstruir um sinal contínuo de uma amostra de um sinal digital. Os conversores digital-analógico utilizam aproximações com os filtros reais
Os filtros passa-baixo eletrônicos[editar | editar código-fonte]

Existem muitos tipos diferentes de circuitos de filtros, com diferentes respostas à mudança de frequência. A resposta em frequência de um filtro é geralmente representada utilizando um gráfico.
- Um filtro de primeira ordem, por exemplo, irá atenuar a amplitude do sinal em cerca de 6 dB cada vez que a frequência dobrar (subir uma oitava). O gráfico de magnitude de um filtro de primeira ordem se assemelha a uma linha horizontal antes da frequência de corte, e um linha diagonal após a mesma. Existe também o "cotovelo" no limite entre os dois, que é a transição suave entre as duas regiões de reta. Veja Circuito RC.
- Um filtro de segunda ordem possui uma maior atenuação às frequências mais altas. O gráfico deste tipo de filtro é semelhante ao gráfico do filtro de primeira ordem, com a diferença de que a variação na queda da amplitude com o aumento da frequência é mais acentuada. Por exemplo, um filtro Butterworth de segunda ordem reduzirá a amplitude do sinal a um quarto de seu valor anterior cada vez que a frequência dobrar (−12 dB por oitava). Outros filtros de segunda ordem podem apresentar taxas diferentes dependendo de seu fator Q, porém se aproximam da taxa final de −12dB por oitava. Veja Circuito RLC.
- Filtros de terceira ordem ou mais possuem uma definição similar. No geral, a taxa final de atenuação de um filtro de n-ordem é −6n dB por oitava.

Em qualquer filtro Butterworth, se a linha horizontal se estende para a direita e a linha diagonal para a esquerda superior (a assímptota da função), eles terão uma intersecção exatamente na "frequência de corte". A resposta na frequência de corte de um filtro de primeira ordem é de −3 dB com relação à linha horizontal. Os vários tipos de filtros, filtro Butterworth, filtro Chebyshev e outros, possuem "curvas de cotovelo" diferentes. Muitos filtros de segunda ordem são projetados para possuir "pico" ou ressonância, fazendo com que sua resposta em frequência na frequência de corte seja "acima" da linha horizontal. Veja filtro eletrônico para ver os outros tipos.
Os significados de 'baixo' e 'alto', como a frequência de corte, dependem das características do filtro. (O termo "filtro passa-baixo" se refere meramente ao formato da resposta do filtro. Um filtro passa-alto pode ser construído de modo a cortar as frequências menores que as de um filtro passa-baixo. São suas respostas que os diferenciam, não a frequência de corte.) Os circuitos eletrônicos podem ser desenvolvidos para qualquer faixa de frequência desejada, podem atingir inclusive a faixa das micro-ondas (acima de 1000 MHz) ou superior.
Implementação através de componentes passivos[editar | editar código-fonte]
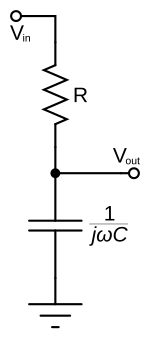
Um circuito eletrônico simples que funciona como um filtro passa-baixo consiste de um resistor em série com um capacitor em paralelo com a carga. O capacitor exibe reatância, e bloqueia os sinais de baixa frequência, fazendo com que eles passem pela carga. A frequências mais altas, a reatância reduz e o capacitor conduz com facilidade. A frequência de corte é determinada pela escolha da resistência e da capacitância:
ou equivalentemente (em radianos por segundo):
Um modo de compreender este circuito é se voltar ao tempo que o capacitor leva para se carregar. O capacitor leva um período de tempo para carregar e descarregar através do resistor:
- A baixas frequências, exige muito tempo para que o capacitor se carregue até atingir praticamente a mesma tensão da entrada.
- A altas frequências, o capacitor tem tempo apenas para uma pequena carga antes que as entradas invertam sua polaridade. A saída sobe e desce apenas uma pequena quantia de tempo com relação às subidas e descidas da entrada. A uma frequência dobrada, existe tempo apenas para que o capacitor se carregue metade do que poderia se carregar antes.
Outra forma de compreender este circuito é com a ideia de reatância em uma frequência particular:
- Como a CC não pode passar através do capacitor, a entrada CC deve "passar" pelo caminho marcado (como se o capacitor tivesse sido removido do circuito).
- Como a CA flui com facilidade pelo capacitor, a entrada CA "passa" através do capacitor, atuando de forma semelhante a um curto-circuito à terra (como se o capacitor tivesse sido substituído por um fio).
Deve-se perceber que o capacitor não é um componente "ligado/desligado" (como a explicação de bloqueio ou passagem acima). O capacitor irá ter uma atuação que varia entre estes dois experimentos, reduzindo a sua impedância com o aumento da frequência. Seu gráfico e sua resposta em frequência mostram esta variação.
Implementação através de componentes ativos[editar | editar código-fonte]

Outro tipo de circuito eletrônico é o filtro passa-baixo "ativo" de 1ª ordem (apenas 1 polo).
Neste exemplo, a frequência de corte (em hertz) é definida como:
ou equivalentemente (em radianos por segundo):
O ganho deste filtro é , e o ganho cai em −6 dB por oitava, assim como no filtro de primeira ordem.
Muitas vezes, um ganho simples ou um amplificador de atenuação (Veja amplificador operacional) é transformado em um filtro passa-baixo através da adição do capacitor C. Isto reduz a resposta em frequência a altas frequências e ajuda e eliminar oscilações no amplificador. Por exemplo, um amplificador de áudio pode ser montado como um filtro passa-baixo com frequência de corte igual a 100 kHz para reduzir o ganho nas frequências que o fariam oscilar. Como a banda audível vai até cerca de 20 kHz. todas as frequências de interesse estão inclusas na banda passante, e o amplificador atua da mesma forma para os sinais de áudio.






