Ressonância
| Mecânica clássica |
|---|
 Diagramas de movimento orbital de um satélite ao redor da Terra, mostrando a velocidade e aceleração. |
|
Cinemática |
|
História |
|
Colisões |
|
Sistemas Clássicos |
Em física, ressonância é o fenômeno em que um sistema vibratório ou força externa conduz outro sistema a oscilar com maior amplitude em frequências específicas, conhecidas como frequências ressonantes ou frequências naturais do sistema. Nessas frequências, até mesmo forças periódicas pequenas podem produzir vibrações de grande amplitude, pois o sistema armazena energia vibracional.
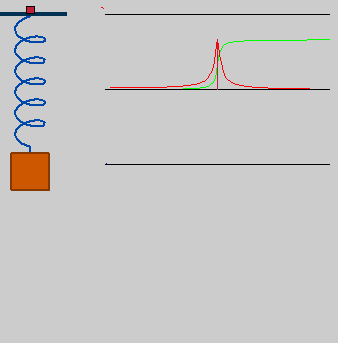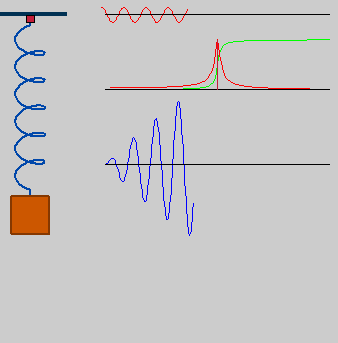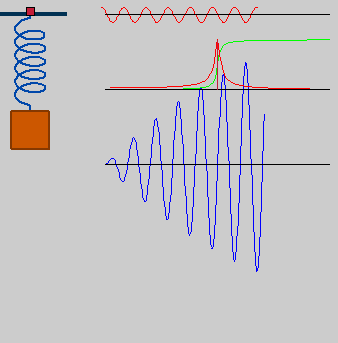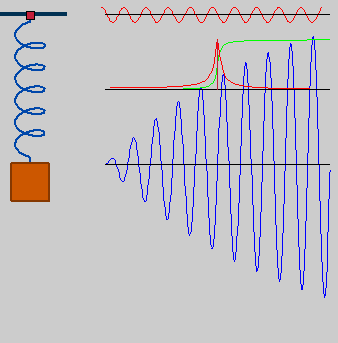
Um oscilador harmônico simples possui uma frequência angular natural relacionada com as características do sistema em questão. Quando o oscilador harmônico simples está sujeito a uma força externa periódica e contínua, o denominamos de oscilador forçado. Dependendo da frequência dessa força, pode ocorrer efeito ressonante.
Interpretaremos num primeiro momento a ressonância de maneira idealizada, ou seja, não levaremos em conta as perdas de energia ocasionadas por atrito, por exemplo. Então, de maneira simplificada, a ressonância ocorre em um sistema quando o mesmo está sujeito a uma força externa contínua e periódica cuja periodicidade está diretamente relacionada com a frequência natural do sistema. Nesse caso, o sistema produzirá grandes amplitudes.
Contudo, a realidade não é tão simples, existem algumas perdas de energia de período a período, a qual denominamos de amortecimento. Quando o amortecimento é pequeno, a frequência de ressonância do sistema é aproximadamente igual à frequência natural do sistema.
Os sistemas possuem múltiplas e distintas frequências de ressonância e esse fenômeno ocorre com todos os tipos de vibrações ou ondas; mecânicas (acústicas), eletromagnéticas, e funções de onda quântica. Sistemas ressonantes podem ser usados para gerar vibrações de uma frequência específica, ou para obter frequências específicas de uma vibração complexa contendo muitas frequências.
A ressonância foi descoberta por Galileu Galilei quando começou suas pesquisas com pêndulos e cordas musicais no começo de 1602. Outros acreditam que Pitágoras foi o pioneiro no assunto muito antes durante sua vida entre 570 - 495 anos a.C. especialmente na investigação sobre teorias musicais.
Exemplos[editar | editar código-fonte]
- Ressonância mecânica;
- Ressonância elétrica;
- Ressonância óptica;
- Ressonância orbital em astronomia;
- Ressonância Molecular;
- Ressonância Acústica.
Oscilações forçadas[editar | editar código-fonte]
Com o intuito de apresentar uma base introdutória clara sobre ressonância, e para fins práticos, falaremos sobre ressonância no que concerne a perspectiva de osciladores harmônicos forçados. A ressonância elétrica possui a mesma equação que a ressonância em um sistema massa-mola, porém, com outras variáveis. Esse exemplo ilustra o fato de que a equação de ressonância é a mesma tanto para o caso elétrico, para o caso mecânico, quanto para os demais casos, a não ser pelas respectivas variáveis.[1]
Descrição teórica da ressonância em oscilações forçadas[editar | editar código-fonte]

Uma criança que se diverte em um balanço sem que ninguém a empurre constitui um exemplo de oscilação livre. Contudo, se a esse movimento for acrescentado uma força externa periódica, dizemos que a criança estará executando uma oscilação forçada, e dependendo da frequência da força a amplitude do movimento pode aumentar ou diminuir. Como veremos a seguir, a amplitude aumentará quando a frequência da força externa é a mesma da frequência natural do sistema. É o caso que aplicamos uma força externa periódica - empurramos a criança toda vez que o balanço se encontrar no máximo de altura (máxima energia potencial - com a mesma frequência do movimento livre.[2]

A um sistema que executa oscilações forçadas podemos associar duas frequências angulares (as relações matemáticas entre os termos físicos estão explicitados abaixo): uma delas está de acordo com a frequência angular das oscilações livres do sistema, ou seja, é a frequência natural do sistema adquirido a partir de uma perturbação curta; e a outra está associada com a frequência angular da força externa (contínua e periódica) que produz a oscilação forçada.[2] Note que em um momento falamos sobre frequência angular natural e em outro apenas sobre frequência natural. Isso se deve pelo fato de que as duas grandezas estão relacionadas por uma constante , descritas a seguir:
A amplitude do sistema de oscilação forçada ideal é máxima quando a frequência angular da força externa é igual à frequência angular natural do sistema. Essa situação caracteriza um caso de ressonância, na qual o sistema passa a oscilar com um amplitude crescente. Na verdade, como veremos na interpretação matemática, essa amplitude seria infinita. O sistema não atinge essa amplitude devido a alguns outros termos de atrito e resistência do material que não foram considerados.[1]

Para um sistema que sofre oscilação forçada com amortecimento (caso real), percebemos que o menor amortecimento está associado a um pico de ressonância mais alto. Esse caso está ilustrado no gráfico ao lado.
Apesar de termos usado o exemplo particular da criança no balanço como interpretação simplificada da ressonância, podemos generalizar as implicações para outros diversos casos em muitos campos diferentes, e também perceberíamos que as equações seriam as mesmas. Existem muitas situações na natureza na qual algo está oscilando e na qual o fenômeno de ressonância ocorre.[1] Todas as estruturas mecânicas possuem uma ou mais frequências naturais de vibração. Se a estrutura é submetida a forças periódicas de mesma frequência ou próxima a frequência natural pode ocorrer o efeito de ressonância, de forma mais brusca ou não dependendo do amortecimento do sistema, e isso pode causar a ruptura da estrutura.[2] Para efeitos de interpretação, a força externa poderia ser a força causada por um terremoto, nesse caso.
Descrição matemática da ressonância em oscilações forçadas[editar | editar código-fonte]
Requisitos[editar | editar código-fonte]
- 2ª Lei de Newton:
- A frequência das oscilações será dada pela seguinte relação:
- Identidades:
: frequência natural do sistema em questão; : frequência da força externa;
- Se definirmos , então a a equação do oscilador harmônico simples poderá ser escrita do seguinte modo:
- Solução homogênea da equação do oscilador harmônico simples:
Descrição matemática[editar | editar código-fonte]
A seguir discutiremos o oscilador harmônico forçado. A equação então é a seguinte:
Sabemos que a solução da parte homogênea dessa equação diferencial, ou seja, a solução (usando ) de:
é:
Precisamos descobrir qual é a solução particular referente a força externa .
A força externa pode ter diversos tipos de dependências funcionais com diferentes frequências. Tentaremos resolver a equação com uma força especial, uma força oscilante:
Note que não é necessariamente o mesmo que . Temos sob o nosso controle; Então devemos resolver tal equação. Com conhecimento prévio de equações diferenciais percebemos que uma solução particular é do tipo:
, onde a constante é para ser determinada.
Então jogamos essa solução na equação do oscilador harmônico forçado com explicito. Colocamos também e encontraremos:
Como o cosseno aparece em todos os lugares, podemos dividir a equação toda por ele e mostrar que a solução especial é, de fato, uma solução, se escolhermos o corretamente. A resposta é que deve ser

Então a solução particular é:
De fato, a solução geral do oscilador harmônico forçado será a soma da solução particular com a solução da equação homogênea:
Notemos, então, que quando a frequência angular da força externa se aproxima do valor da frequência angular natural do sistema sob oscilação livre, teremos um fator periódico com uma amplitude que tende ao infinito. Sabemos que não existe nenhum sistema que chegaria a esse ponto, pois além dele se partir antes, existem outros termos de atrito e outras forças que não consideramos por fins práticos mas que acontecem no tempo real.[1] Ao somarmos a solução particular com a solução do caso homogêneo, percebemos que existe a concordância com o Princípio da Superposição das Ondas. Podemos interpretar essa situação, em que o sistema não pode atingir uma amplitude infinita, pela perspectiva do Princípio da Superposição das Ondas: só pode existir a sobreposição de ondas até o momento que o sistema em questão permitir, ou seja, o quanto a estrutura do material suporta, por exemplo.[2] De fato estamos interessados no resultado qualitativo de tal equação. Chegamos num resultado que está de acordo com a explicação teórica acima e que configura o efeito de ressonância.
Descrição matemática 2[editar | editar código-fonte]
Podemos, também, interpretar o caso de ressonância a partir de uma força externa periódica que já tenha a mesma frequência angular natural do sistema,[3] o que é diferente do primeiro caso, no qual consideramos que a força externa não possuía a mesma frequência angular natural do sistema, mas que a fazíamos assumir o valor ao analisarmos a solução geral. Então, a partir dessa perspectiva, podemos considerar a força externa como:
Assim, percebemos que existe uma similaridade dessa solução, com a solução que já conhecemos da parte homogênea que é:
Com o conhecimento de equações diferenciais é fácil perceber que a solução particular referente a força externa precisa ser da seguinte forma para produzirmos soluções linearmente independentes:
, onde a constante é para ser determinada. Substituindo a equação da solução particular na equação do sistema, encontramos a seguinte constante referente a força externa:
Então, a solução geral é da forma:[3]
E, novamente, percebemos que a força externa passa a governar o sistema se se considerar tempos sucessivos, na qual a amplitude do termo periódico na solução geral, referente a força externa, só tende a aumentar com o decorrer do tempo. Chegamos, mais uma vez, num resultado que está de acordo com a explicação teórica acima e que configura o efeito de ressonância.






























