Mecânica de Lagrange
| Mecânica clássica |
|---|
 Diagramas de movimento orbital de um satélite ao redor da Terra, mostrando a velocidade e aceleração. |
|
Cinemática |
|
História |
|
Colisões |
|
Sistemas Clássicos |
A mecânica de Lagrange ou mecânica lagrangiana, nomeada em honra ao seu conceptor, Joseph-Louis Lagrange, é uma formulação da mecânica clássica que combina a conservação do momento linear com a conservação da energia. Exposta pela primeira vez no livro Méchanique Analytique em 1788, a formulação é provida de um potente ferramental matemático equivalente a qualquer outra formulação da mecânica, como por exemplo, o formalismo newtoniano.
Na mecânica lagrangiana, a trajetória de um sistema de partículas é obtida resolvendo as equações de Lagrange em uma de suas duas formas, chamadas equações de Lagrange de primeiro tipo,[1] que trata as restrições explicitamente como equações adicionais, geralmente utilizando os multiplicadores de Lagrange;[2][3] e as equações de Lagrange de segundo tipo, que incorporam as restrições diretamente na escolha das coordenadas generalizadas.[1][4] O lema fundamental do cálculo das variações mostra que resolver as equações de Lagrange é equivalente a encontrar o caminho que minimiza a funcional ação, uma quantidade que é a integral da função de Lagrange no tempo.
Dado um conjunto de coordenadas generalizadas para descrever o sistema físico estudado, a lagrangiana de qualquer sistema o caracteriza de forma unívoca e pode apresentar as seguintes dependências funcionais , em que que são as velocidades generalizadas.
Pelo Princípio de Hamilton,[5] que nos diz que o trajeto real da partícula,[6] entre os instantes e é aquele que minimiza a ação . Fixados os extremos da trajetória no espaço de configuração. Encontramos [7] as equações de Euler-Lagrange
que são equações diferenciais parciais de segunda ordem em .
No caso de um sistema não-conservativo (ou dissipativo), temos
em que são as forças generalizadas externas.
A mecânica lagrangiana é baseada num formalismo escalar mais simples e geral, quando comparado ao formalismo vetorial de Newton. Com isso, ela é capaz de descrever igualmente bem fenômenos a baixas velocidades ou a velocidades relativísticas. O único aspecto que difere entre cada caso é a Função de Lagrange.
Uma escolha para as coordenadas generalizadas[editar | editar código-fonte]

Em um sistema clássico, por exemplo, temos que (aqui estamos assumindo que as coordenadas generalizadas são os módulos dos vetores posição de cada partícula que compõem o sistema) e a função de Lagrange é definida por:[8]
,
em que é a energia cinética e é a energia potencial.
Quanto às equações de Euler-Lagrange, temos
Aplicação "clássica"[editar | editar código-fonte]
A mecânica de Lagrange tem a vantagem de resolver elegantemente problemas complexos, sendo um bom exemplo do grau de abstração embutido no formalismo de Lagrange a simplicidade com que podemos deduzir as leis de conservação a partir das simetrias do espaço-tempo. Deixa-se, aqui, a título de exemplo, a dedução da Conservação do Momento Linear:
- Conservação do Momento Linear
Sendo o espaço homogêneo,[9] tem-se que . Num sistema isolado (conservativo), pelas equações de Euler-Lagrange, temos . Definindo [10], chegamos a
Princípio de D'Alembert e forças generalizadas[editar | editar código-fonte]

O Princípio de D'Alembert introduz o conceito de Força Virtual ou Trabalho Virtual devido a aplicação de forças F i e forças inerciais, agindo em um sistema tri-dimensional acelerado de n partículas que em movimento é consistente com as suas limitações,[11]
Matematicamente, o trabalho virtual feito AW em uma partícula de massa através de um deslocamento virtual δ r i (consistente com as restrições) é:
Princípio de D'Alembert
onde são as acelerações das partículas no sistema i = 1, 2,...,n simplesmente rotulam as partículas. Em termos de coordenadas generalizadas
essa expressão sugere que as forças aplicadas possam ser forças generalizadas, Qj. Dividindo por δqj da a definição de uma força generalizada:[11]:265
Se as forças Fi são Força conservativa, há um campo escalar potencial V em que o gradiente de V é a força:[11]:266 & 270
Forças generalizadas podem ser reduzidas para um gradiente de potencial em termos de coordenadas generalizadas. O resultado anterior pode ser mais fácil de ver, reconhecendo que V é a função de ri, que por sua vez são funções de qj, e, em seguida aplicando a Regra da cadeia para a derivada de em relação a qj.
Relações de energia cinética[editar | editar código-fonte]
A energia cinética, T, para o sistema de partículas é[11]:269
As derivadas parciais de T em relação às coordenadas generalizadas e velocidades generalizadas são [11]:269:
Porque e são variáveis independentes:
Então :
O Tempo total derivado desta equação é:
resultando em:
Equações de movimento generalizadas
Esta é uma importante equação. As leis de Newton estão contidas nela e não existe nenhuma necessidade de encontrar as forças de restrição, porque o trabalho virtual e coordenadas generalizadas (que representam restrições) são usados. Esta equação em si não é realmente usada na prática, mas é um passo para derivar as equações de Lagrange.[12]
Lagrangiano e ação[editar | editar código-fonte]
O elemento central da mecânica de Lagrange é a função de Lagrange, função que resume a dinâmica de todo o sistema em uma expressão muito simples. A física de análise de um sistema é reduzida para a escolha do conjunto mais conveniente de coordenadas generalizadas, determinando as energias potencial e cinética dos constituintes do sistema, então escrevemos a equação do lagrangiano nas equações de Lagrange. Que é definido pela[13]
onde T é o total de energia cinética V é o total de energia potencial do sistema.
O próximo elemento fundamental é a ação , definida como a integral do lagrangiano no tempo:
Este contém também a dinâmica do sistema, e tem implicações teóricas profundas. Formalmente a ação não é uma função, mas um funcional: seu valor depende da função de Lagrange em todos os instantes entre t1 e t2. Sua dimensão é a mesma do momento angular.
Na teoria de campos, a densidade lagrangiana deve ser utilizada:
e a ação torna-se um integral no espaço e no tempo:
Derivação de equações de Lagrange[editar | editar código-fonte]
Princípio de Hamilton[editar | editar código-fonte]
As equações de Euler-Lagrange seguem diretamente o princípio de Hamilton, e são matematicamente equivalentes. A partir do cálculo das variações, qualquer funcional da forma:
leva à equação geral de Euler-Lagrange para o valor estacionário de J:
Então, fazendo as substituições:
se produz as equações de Lagrange para a mecânica. Como, matematicamente, as equações de Hamilton podem ser derivadas a partir de equações de Lagrange e as equações de Lagrange podem ser derivadas a partir das Leis de Newton, as quais são equivalentes e resumem a mecânica clássica, podemos observar que a mecânica clássica é fundamentalmente governada por um princípio de variação (princípio de Hamilton acima).
Forças generalizadas[editar | editar código-fonte]
Para um sistema conservativo, uma vez que o campo de potencial é só uma função da posição, não a velocidade, as equações de Lagrange também se seguem diretamente a partir da equação de movimento acima:
simplificando temos
Isto é consistente com os resultados obtidos acima, e pode ser visto através da diferenciação do lado direito do lagrangiano em relação à e tempo, e somente com relação a qj, somando os resultados e associando um acordo com as equações de Fi e Qj.
Princípio de Hamilton de ação estacionária[editar | editar código-fonte]
Deixemos q0 e q1 serem as coordenadas em respectivos tempos iniciais e finais t0 e t1. Usando o Cálculo das variações, pode-se mostrar que as equações de Lagrange são equivalentes ao princípio de Hamilton:
- A trajetória do sistema entre t0 e t1 tem uma 'ação estacionária' S.
Por estacionário, queremos dizer que a ação não varia da primeira ordem para deformações infinitesimais da trajetória, com os pontos finais (q0, t0) e (q1,t1) corrigidos. O Princípio de Hamilton pode ser escrito como:
Assim, em vez de pensar sobre partículas aceleradas em resposta a forças aplicadas, pode-se pensar nelas escolhendo o caminho com uma ação estacionária.
O Princípio de Hamilton é muitas vezes referido como oprincípio da mínima ação. No entanto, a ação funcional só precisa ser estacionária, não necessariamente a um valor máximo ou mínimo. Qualquer variação das funcionais resulta em um aumento na integral funcional da ação.
Podemos usar este princípio em vez de as leis de Newton como o princípio fundamental da mecânica, o que nos permite usar um princípio integral (leis de Newton são baseadas em equações diferenciais para que elas sejam um princípio diferencial) como base para a mecânica.
Equações de Lagrange do primeiro tipo[editar | editar código-fonte]
Lagrange introduziu um método analítico para encontrar pontos fixos, utilizando o método de multiplicadores de Lagrange , e isto também se aplica à mecânica.
Para um sistema sujeito à equação de restrição nas coordenadas generalizadas:
onde A é uma constante, então as equações de lagrange do primeiro tipo são:
onde λ é o multiplicador de Lagrange. Por analogia com o procedimento matemático, podemos escrever:
onde
denota a Derivada variacional
Para e equações de restrição F1, F2,..., Fe, existe um multiplicador de Lagrange, para cada equação de restrição, e as equações do primeiro tipo de Lagrange a generalizar são:
Equações de Lagrange (1º tipo)
Este procedimento faz aumentar o número de equações, mas ainda não são suficientes para resolver todos os multiplicadores. O número de equações é gerado o número de equações de restrição adicional, o número de coordenadas, e + m. A vantagem do método é que (potencialmente complicada) a substituição e eliminação das variáveis ligadas por equações de restrição podem ser ignoradas.
Existe uma ligação entre as equações de restrição Fj e as forças de restrição Nj atuando no conservador do sistema (as forças são conservadoras):
que é derivado a seguir.
Derivação de conexão entre as equações de restrição e as forças As forças de restrição são indicadas pela definição da força generalizada acima: e usando a equação da energia cinética do movimento:
Para sistemas conservadores (ver abaixo)
então
e
igualando leva à
e, finalmente, equivalendo a equações do primeiro tipo de Lagrange ,implica:
Assim, cada equação de restrição corresponde a uma força de restrição (num sistema conservador).
Equações de Lagrange do segundo tipo[editar | editar código-fonte]
Equações de Euler-Lagrange[editar | editar código-fonte]
Para qualquer sistema com m graus de liberdade, as equações de Lagrange incluem M coordenadas generalizadas e M velocidades generalizadas. Abaixo, vamos esboçar a derivação das equações de Lagrange do segundo tipo. Nesse contexto, V é usado ao invés de U para energia potencial e T substitui K de energia cinética.
As equações de movimento na mecânica de Lagrange são as equações lagrangianas do segundo tipo', também conhecidas como as Equações de Euler-Lagrange:[14]
Equações de Lagrange (2º tipo)
onde j = 1, 2,...m representa o j grau de liberdade, qj são as coordenadas generalizadas, e são as velocidades generalizadas.
Embora a matemática necessária para equações de Lagrange pareça muito mais complicada do que as leis de Newton, isso aponta para uma percepção mais profunda do que as leis da mecânica clássica de Newton só: em particular, conceitos como simetria e conservação. Na prática, muitas vezes é mais fácil de resolver um problema usando as equações de Lagrange do que as leis de Newton, pois as coordenadas generalizadasqi podem ser escolhidas por conveniência para explorar simetrias no sistema, e as forças de restrição são incorporadas na geometria do problema. Existe uma equação de Lagrange para cada coordenada generalizada qi.
Para um sistema de muitas partículas, cada partícula pode ter diferentes números de graus de liberdade do que os outros. Em cada uma das equações de Lagrange, T é o total da energia cinética do sistema, e V o total da energia potencial.
Derivação das equações de Lagrange[editar | editar código-fonte]
Princípio de Hamilton[editar | editar código-fonte]
As equações de Euler-Lagrange se seguem diretamente do princípio de Hamilton, e são matematicamente equivalentes.Do cálculo das variações, qualquer funcional da forma:
leva à geral equação de Euler-Lagrange para o valor estacionário de J:
Em seguida, fazendo as substituições:
produz as equações de Lagrange para a mecânica. Desde que matematicamente as equações de Hamilton podem ser derivadas a partir de equações de Lagrange (por uma transformação de Legendre) e as equações de Lagrange podem ser derivadas a partir de leis de Newton, as quais são equivalentes em resumir a mecânica clássica, isto significa que mecânica clássica é fundamentalmente governada por um princípio de variação (princípio de Hamilton acima).
Forças generalizadas[editar | editar código-fonte]
Para um sistema conservativo, uma vez que o campo de potencial é só uma função da posição, não a velocidade, as equações de Lagrange também seguem diretamente a partir da equação de movimento acima:
simplificando a
Isto é consistente com os resultados obtidos acima e pode ser vista por diferenciação do lado direito do lagrangiano com relação a e tempo, e somente com relação ao qj, somando os resultados e associando um acordo com as equações para Fi e Qj.
As leis de Newton[editar | editar código-fonte]
Como os seguintes derivação mostraram, nenhuma nova física é introduzida, então as equações de Lagrange podem descrever a dinâmica de um sistema clássico equivalentemente como as leis de Newton.
Derivação das equações de Lagrange da 2 ª lei de Newton e o princípio de D'Alembert - Força e trabalho feitos (sobre a partícula)
Considere uma única partícula com massa m e o Vetor posição r, movendo-se sob uma aplicada Força conservativa F, que pode ser expressada como o gradiente de um escalar energia potencial função V(r, t):
Tal força é independente da terceira ou de ordem superior derivados de r.
Considere um deslocamento arbitrário δr da partícula. O Trabalho feito pela força aplicada F é
- .
Usando a segunda lei de Newton:
Desde que o trabalho é uma grandeza escalar física, devemos ser capazes de reescrever esta equação em termos das coordenadas generalizadas e velocidades. No lado esquerdo,
No lado direito, a realização de uma alteração de coordenadas para coordenadas generalizadas, obtemos:
Agora a Integração por partes o somatório em relação a t, em seguida, a diferenciação com respeito a t:
permite que a soma seja escrita como:
Reconhecendo que
Nós obtemos:
- A energia cinética e potencial
Agora, alterando a ordem de diferenciação, obtém-se:
Finalmente, alterando a ordem da soma:
O que equivale a:
onde T é o total de energia cinética do sistema
- Aplicando o Princípio de d'Alembert
A equação para o trabalho torna-se
No entanto, isso deve ser verdadeiro para qualquer conjunto dos deslocamentos generalizados δqi,por isso devemos ter
para cada coordenada generalizada δqi.Podemos simplificar ainda mais notando que V é uma função exclusiva de r e t, e r é uma função das coordenadas e generalizada t. Portanto, V é independente das velocidades generalizadas:
Introduzindo esta na equação anterior e substituindo L = T − V,chamado de Lagrangiano, obtemos as equações de Lagrange:
Quando qi = ri (as coordenadas generalizadas são simplesmente as coordenadas cartesianas), é fácil verificar que as equações de Lagrange reduzem para a segunda lei de Newton.
Função da dissipação[editar | editar código-fonte]
Numa formulação mais geral, as forças poderiam ser tanto potenciais e viscosas. Se uma transformação apropriada podem ser achada da Fi, indica-se usar um a função de dissipação, D, na seguinte forma:
onde Cjk elas são constantes que são relacionados com os coeficientes de amortecimento nos sistemas físicos, mas não são iguais a eles necessariamente.
Se D é definido deste jeito:}
então
Massa em queda[editar | editar código-fonte]
Considere um ponto de massa m em queda livre a partir do repouso. Pela gravidade uma força F = mg é exercida nas massas (assumindo g uma constante durante o movimento). O preenchimento da força na relação de Newton, descobrimos que da qual a solução de
segue (tomando a antiderivada da antiderivada e, escolhendo a origem como o ponto inicial). Este resultado também pode ser derivado por meio do formalismo lagrangiano. Tendo x para ser a coordenada em que 0 é ponto de partida.
A energia cinética é T = 1⁄2mv2 e a energia potencial é V = −mgx; logo,
- .
então
a qual pode ser reescrita como , originando o mesmo resultado obtido aplicando-se a mecânica newtoniana.
Pêndulo sobre um suporte móvel[editar | editar código-fonte]
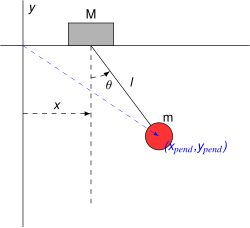
Considere um pêndulo de massa m e comprimento ℓ, que está ligado a um suporte com massa M, que pode se mover ao longo de uma linha na direção x. Seja x a coordenada ao longo da linha de apoio, vamos indicar a posição do pêndulo pelo ângulo θ em relação à vertical.
A energia cinética pode então ser descrita como:
e a energia potencial do sistema é:
O lagrangiano é portanto:
Agora realizando as diferenciações temos o apoio de coordenadas x
portanto:
indicando a presença de uma constante de movimento. Realizando o mesmo procedimento para a variável temos:
portanto
Essas equações podem parecer bastante complicadas, mas encontrá-las com as leis de Newton teria exigido identificar cuidadosamente todas as forças, o que teria sido muito mais trabalhoso e propenso a erros. Ao considerar casos limite, a correção deste sistema pode ser verificada: Por exemplo, deve dar as equações de movimento para um pêndulo que está em repouso em algum inercial, Enquanto deve dar as equações para um pêndulo em um sistema de aceleração constante, etc.
Referências
- ↑ a b R. Dvorak, Florian Freistetter (2005). «§ 3.2 Lagrange equations of the first kind». Chaos and stability in planetary systems. [S.l.]: Birkhäuser. p. 24. ISBN 3540282084
- ↑ H. Haken (2006). Information and self-organization 3ª ed. [S.l.]: Springer. p. 61. ISBN 3540330216
- ↑ Cornelius Lanczos (1986). «II §5 Auxiliary conditions: the Lagrangian λ-method». The variational principles of mechanics Reprint of University of Toronto 1970 4th ed. [S.l.]: Courier Dover. p. 43. ISBN 0486650677
- ↑ Henry Zatzkis (1960). «§1.4 Lagrange equations of the second kind». In: DH Menzel. Fundamental formulas of physics. 1 2ª ed. [S.l.]: Courier Dover. p. 160. ISBN 0486605957
- ↑ Também conhecido como princípio da mínima ação.
- ↑ Se este for o nosso objeto de estudo.
- ↑ Para sistemas conservativos.
- ↑ Thornton, Stephen T.; Marion, Jerry B. (1995). Classical Dynamics of Particles and Systems (em inglês) 4 ed. Fort Worth: Saunders College Publications. ISBN 978-0030973024
- ↑ Ou seja, havendo invariância sob translação espacial no fenômeno estudado.
- ↑ De fato, na mecânica clássica teremos , se somente não for função das velocidades generalizadas.
- ↑ a b c d e Torby, Bruce (1984). «Energy Methods». Advanced Dynamics for Engineers. Col: HRW Series in Mechanical Engineering. United States of America: CBS College Publishing. ISBN 0-03-063366-4
- ↑ Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, ISBN 978-0-521-57572-0
- ↑ Torby1984, p.270
- ↑ The Road to Reality, Roger Penrose, Vintage books, 2007, ISBN 0-679-77631-1
Bibliografia[editar | editar código-fonte]
- MAIA, NUNO M: Introdução à Mecânica Analítica, IST Press
- GOLDSTEIN: Classical Mechanics, Addison-Wesley
- LEMOS, NIVALDO A.: Mecânica Analítica, Livraria da Física, 2ª ed.














































![{\displaystyle Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {(}}L+V)}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial {\mathcal {(}}L+V)}{\partial q_{j}}}=\left[{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)+0\right]-\left[{\frac {\partial L}{\partial q_{j}}}+{\frac {\partial V}{\partial q_{j}}}\right]={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial L}{\partial q_{j}}}+Q_{j}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80309d23e434cd34da4345a4409a39fa6a7ac010)



![{\displaystyle \left[{\frac {\partial L}{\partial r_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {r}}_{j}}}\right)\right]+\lambda {\frac {\partial F}{\partial r_{j}}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cb75e59979cfda8ea6547467835de03b9a3dc69)
















![{\displaystyle m{\ddot {\mathbf {r} }}\cdot \delta \mathbf {r} =m\sum _{j}\left[\sum _{i}{\ddot {r_{i}}}{\partial r_{i} \over \partial q_{j}}\right]\delta q_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e89b4cb3a9e28609873facbaa2b629c8727a50e1)

![{\displaystyle m{\ddot {\mathbf {r} }}\cdot \delta \mathbf {r} =m\sum _{j}\left[\sum _{i}\left[{\mathrm {d} \over \mathrm {d} t}\left({\dot {r_{i}}}{\partial r_{i} \over \partial q_{j}}\right)-{\dot {r_{i}}}{\mathrm {d} \over \mathrm {d} t}\left({\partial r_{i} \over \partial q_{j}}\right)\right]\right]\delta q_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/255229d6b2447b547fa97c5c797a8acf1f817cd4)

![{\displaystyle m{\ddot {\mathbf {r} }}\cdot \delta \mathbf {r} =m\sum _{j}\left[\sum _{i}\left[{\mathrm {d} \over \mathrm {d} t}\left({\dot {r_{i}}}{\partial {\dot {r_{i}}} \over \partial {\dot {q_{j}}}}\right)-{\dot {r_{i}}}{\partial {\dot {r_{i}}} \over \partial q_{j}}\right]\right]\delta q_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a2c5b59be98ca7fa9291de9be417aa2bb705b86)
![{\displaystyle m{\ddot {\mathbf {r} }}\cdot \delta \mathbf {r} =m\sum _{j}\left[\sum _{i}\left[{\mathrm {d} \over \mathrm {d} t}{\partial \over \partial {\dot {q_{j}}}}\left({\frac {1}{2}}{\dot {r_{i}}}^{2}\right)-{\partial \over \partial q_{j}}\left({\frac {1}{2}}{\dot {r_{i}}}^{2}\right)\right]\right]\delta q_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a341f2fe46f9e58c37cd15b6f9978b583025750)
![{\displaystyle m{\ddot {\mathbf {r} }}\cdot \delta \mathbf {r} =\sum _{j}\left[{\mathrm {d} \over \mathrm {d} t}{\partial \over \partial {\dot {q_{j}}}}\left(\sum _{i}{\frac {1}{2}}m{\dot {r_{i}}}^{2}\right)-{\partial \over \partial q_{j}}\left(\sum _{i}{\frac {1}{2}}m{\dot {r_{i}}}^{2}\right)\right]\delta q_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae905db05218a041ad6a08a56a1c39ae4deb4cbd)
![{\displaystyle m{\ddot {\mathbf {r} }}\cdot \delta \mathbf {r} =\sum _{i}\left[{\mathrm {d} \over \mathrm {d} t}{\partial T \over \partial {\dot {q_{i}}}}-{\partial T \over \partial q_{i}}\right]\delta q_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/720a3c504b0bf29404669ee12589ba666087c3e9)
![{\displaystyle m\mathbf {\ddot {r}} \cdot \delta \mathbf {r} -\mathbf {F} \cdot \delta \mathbf {r} =\sum _{i}\left[{\mathrm {d} \over \mathrm {d} t}{\partial {T} \over \partial {\dot {q_{i}}}}-{\partial {(T-V)} \over \partial q_{i}}\right]\delta q_{i}=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/376faa7b6ba8f058de2a4748b2407893b6ff06b7)
![{\displaystyle \left[{\mathrm {d} \over \mathrm {d} t}{\partial {T} \over \partial {\dot {q_{i}}}}-{\partial {(T-V)} \over \partial q_{i}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f35602e82b06cc166a95fe5286442b787b673ad6)









![{\displaystyle {\begin{aligned}T&={\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left({\dot {x}}_{\mathrm {pend} }^{2}+{\dot {y}}_{\mathrm {pend} }^{2}\right)\\&={\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left[\left({\dot {x}}+\ell {\dot {\theta }}\cos \theta \right)^{2}+\left(\ell {\dot {\theta }}\sin \theta \right)^{2}\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bba26a81160e526ba09256f808cb65831b6ac518)

![{\displaystyle {\begin{aligned}L&=T-V\\&={\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left[\left({\dot {x}}+\ell {\dot {\theta }}\cos \theta \right)^{2}+\left(\ell {\dot {\theta }}\sin \theta \right)^{2}\right]+mg\ell \cos \theta \\&={\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}+m{\dot {x}}\ell {\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^{2}{\dot {\theta }}^{2}+mg\ell \cos \theta \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7b790706b97cb8d6fafd6e78350ced32325e723)
![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left[(M+m){\dot {x}}+m\ell {\dot {\theta }}\cos \theta \right]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a25d3d545ea517d7cf66ddac264940eb0042b8b)


![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left[m({\dot {x}}\ell \cos \theta +\ell ^{2}{\dot {\theta }})\right]+m\ell ({\dot {x}}{\dot {\theta }}+g)\sin \theta =0;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27ef95240aa335e09f85c8c7ef67a7301547c588)



