Movimento harmônico simples
| Mecânica clássica |
|---|
 Diagramas de movimento orbital de um satélite ao redor da Terra, mostrando a velocidade e aceleração. |
|
Cinemática |
|
História |
|
Colisões |
|
Sistemas Clássicos |
O movimento harmônico simples (MHS) é o movimento oscilatório periódico ocorrido quando a aceleração e a força resultante são proporcionais e opostas ao deslocamento. É um tipo de frequência do movimento, onde oscila a massa.[1] É explicável por um modelo matemático para alguns movimentos vibratórios observáveis em alguns fenômenos (pêndulo ou vibração molecular).[2]
Num modelo físico construído com molas, o movimento harmônico simples é observável em massas presas a uma mola ligada a um suporte rígido, como uma parede. Se o sistema está na posição de repouso, diz-se em equilíbrio estático.[1] No entanto, se a massa é deslocada a partir da posição de equilíbrio, uma reposição da mesma vai ser exercida pela mola, chamada de elasticidade, seguindo assim a lei de Hooke.[3]
Matematicamente, a força resultante F é dada a partir de onde F é uma força elástica exercida por uma mola (no SI: Newton N, k na Lei de Hooke (N·m−1), e x que é o deslocamento a partir da posição de equilíbrio (em m).[1] Contudo, para qualquer movimento harmônico simples, determina-se que quando o sistema é deslocado de sua posição de equilíbrio, uma força restauradora que obedece à lei de Hooke tende a restaurar o sistema para esse equilíbrio. Uma vez que a massa é deslocada da sua posição de equilíbrio, experimenta uma força resultante de restauração. Como resultado, ela acelera e começa a voltar à posição de equilíbrio.
Quando a massa se aproxima da posição de equilíbrio, a força restauradora diminui. Na posição de equilíbrio, a força resultante restaurada desaparece. No entanto, em x= 0, a força da massa não desaparece devido ao impulso da força restauradora que agiu sobre ele. Portanto, a massa continua além da posição de equilíbrio, comprimindo a mola. Então, a força resultante restaurada tende a desacelerar, até a sua velocidade desaparecer, tentando chegar novamente à posição de equilíbrio.[1]
Dinâmica[editar | editar código-fonte]


Para o movimento harmônico simples unidimensional, a equação dos movimentos é aplicada à segunda lei linear com uma equação diferencial ordinária com seus coeficientes constantes, a partir da segunda lei de Newton e da lei de Hooke.
onde m é a massa inercial com a oscilação do corpo, x é o vetor de deslocamento para o equilíbrio estático e k é a constante elástica, sendo:
Abaixo, uma resolução da equação diferencial, obtendo-se um senoide como solução:
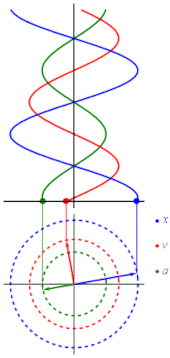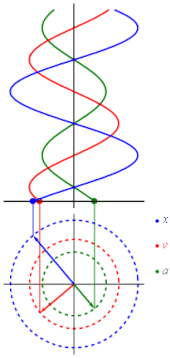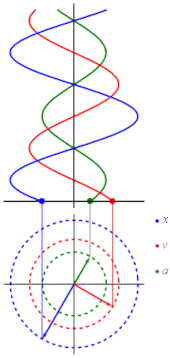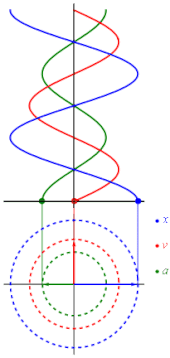
onde
Na solução, c1 e c2 são duas constantes determinadas nas condições iniciais e a sua origem está levando a uma posição de equilíbrio. Cada uma destas constantes leva a um padrão físico ao movimento: A é a amplitude (deslocamento máximo da posição de equilíbrio), é a sua frequência angular, e φ é uma fase. Usando as técnicas do cálculo diferencial, a velocidade e a aceleração têm uma das seguintes funções de tempo:
A aceleração pode ser expressado pela função de deslocamento:
Já que ,
e que T = 1/f onde T é o período de tempo,
Estas equações demonstram que o movimento simples harmônico é isócrono (o período e a frequência são independentes da amplitude e da fase inicial do movimento).[1]
Energia[editar | editar código-fonte]
A energia cinética K de um sistema em função do tempo t é:
e a energia potencial é:
A adição entre a energia cinética e potencial no cálculo da energia mecânica é medida por:
- .[4]
Aplicações[editar | editar código-fonte]
Abaixo tem alguns exemplos de sistemas que usam o movimento harmônico simples:
Massa na mola sob ação da gravidade[editar | editar código-fonte]

Considere um bloco de massa m equilibrado por uma mola constante k sob ação da gravidade. Na situação de equilíbrio, a força gravitacional e a força elástica se igualam. Matematicamente, , onde é a posição natural da mola e é a aceleração devido à gravidade. Note que se conforme se espera. Assim, a posição de equilíbrio se desloca por uma distância .
O que ocorre quando o sistema é deliberadamente retirado da posição de equilíbrio e depois abandonado? A força exercida pela mola atua no sentindo de restaurar à posição natural: assim o objeto oscila verticalmente. Pela segunda lei de Newton podemos escrever
onde é a aceleração (vertical) da mola e é a posição natural (onde a força restauradora é nula). A força gravitacional sempre em direção ao solo enquanto a força da mola só aponta para o solo se .
Podemos simplificar através de uma mudança de variável. Seja , então a segunda derivada (aceleração) é , pois todos os demais termos são constantes. Assim, a equação se transforma na equação do movimento harmônico simples:
.
Nesta variável o movimento é harmônico simples com período . Desta maneira, evidencia-se que o período de oscilação é independente tanto da amplitude quanto da aceleração gravitacional. Vamos supor que as condições iniciais sejam tais que
,
onde é a amplitude e é a frequência angular da oscilação. Para saber como o bloco se desloca no mundo físico devemos voltar para a variável inicial . Assim
é a equação de movimento de um bloco oscilando devido à força elástica de uma mola sob ação da gravidade.
A conclusão é que (1) o movimento tem o mesmo período independente da amplitude e da gravidade[1], e (2) o bloco oscila com amplitude , mas entre os pontos e .
Movimento circular uniforme[editar | editar código-fonte]
O movimento harmônico simples pode ser muitas vezes considerado como uma projeção matemática do movimento circular uniforme. Se um objeto se movimenta com uma velocidade angular ω ao redor de um círculo de um raio r centralizado de uma origem de um plano de x-y, este movimento é em cada coordenada um movimento simples harmônico com uma amplitude r e uma frequência angular ω.[1]
Pêndulo simples em regime de pequenas oscilações[editar | editar código-fonte]

Considere um objeto preso a uma haste inextensível oscilando sob ação da força gravitacional. A este sistema denominamos Pêndulo Simples. De maneira geral, atuam sob o objeto a força de tração da haste, que o mantém oscilando em um arco de círculo a uma distância fixa do ponto fixo que prende a haste ao teto; e também a força gravitacional . Decompomos a força gravitacional de forma que conhecemos a componente na direção da força de tração, que nos fornece , e também a componente responsável pelo movimento
Assim, a força restaura o objeto para a situação de ângulo nulo, , mas o problema se torna mais difícil por tratar com uma função trigonométrica.
Iremos então tomar um caso especial, a situação de pequenos ângulos. Neste caso, e eliminamos a função trigonométrica. Note que a distância horizontal é dada por de forma que neste regime (e apenas neste regime), podemos escrever:
.

Compare esta expressão à Lei de Hooke. Um pêndulo simples é equivalente a um oscilador linear. A constante de reconstituição seria igual à . Substituindo o valor de na fórmula do período de um movimento harmônio simples se obtém
,
,
[1].
Resumidamente, para deduzir a equação do período, estabelece-se que o ângulo θ descrito pelo pêndulo de sua posição de repouso até sua amplitude máxima seja menor que 10°, assim é possível aproximar o valor do ângulo com seu seno.
Reescrevendo as equações do movimento harmônico simples para torná-las mnemônicas[editar | editar código-fonte]
| Aplicação | Variáveis | Fórmula |
|---|---|---|
| Massa na mola | ||
| Aceleração centrípeta | ||
| Pêndulo | [1] | |
| Oscilador LC | ||
| Oscilador RLC paralelo | ||
Ver também[editar | editar código-fonte]
Referências
- ↑ a b c d e f g h i TIPLER, Paul; MOSCA, Gene (2009). Física para cientistas e engenheiros 6 ed. Rio de Janeiro: LTC. p. 466. ISBN 978-85-216-1710-5
- ↑ WALKER, Jearl (2011). Principles of physics 9 ed. Hoboken: Wiley. ISBN 0-470-56158-0
- ↑ TIPLER, Paul; MOSCA, Gene (2009). Física para cientistas e engenheiros 6 ed. Rio de Janeiro: LTC. p. 114. ISBN 978-85-216-1710-5
- ↑ Jain 2009, p. 12




























































