Energia mecânica
física foi marcada para revisão devido a incoerências ou dados de confiabilidade duvidosa. (Agosto de 2011) |
| Mecânica clássica |
|---|
 Diagramas de movimento orbital de um satélite ao redor da Terra, mostrando a velocidade e aceleração. |
|
Cinemática |
|
História |
|
Colisões |
|
Sistemas Clássicos |

Energia mecânica é, resumidamente, a capacidade de um corpo produzir trabalho.[1] Também podemos interpretá-la como a energia que pode ser transferida por meio de uma força. A energia mecânica total de um sistema é a soma da energia cinética, relacionada ao movimento de um corpo, com a energia potencial, relacionada ao armazenamento, podendo ser gravitacional ou elástica.[1]
Se o sistema for conservativo, ou seja, apenas forças conservativas atuarem nele, a energia mecânica total conserva-se e é uma constante de movimento[1]. A energia mecânica que um corpo possui é a soma da sua energia cinética com sua energia potencial .
Uma força é classificada como sendo conservativa quando o trabalho realizado por ela para mover um corpo de um lugar a outro é independente do percurso, isto é, do caminho escolhido. Esclarecendo: para carregar um saco de batatas e o transportar morro acima, o caminho escolhido pode ser mais longo, caminhando-se circularmente ou seguindo um caminho mais curto e reto, mas através de uma ladeira íngreme. A força gravítica é conservativa. Um exemplo de força não conservativa é a força de atrito, que também é chamada de força dissipativa.
Pela lei da conservação da energia, se um corpo está apenas sob a ação de forças conservativas, a sua energia mecânica () conservar-se-á. Isso equivale a dizer, neste caso, que se a energia cinética de um corpo aumentar, a energia potencial deve diminuir e vice-versa, de modo a manter constante.
Considere que uma bola de massa na mão de uma pessoa está a uma altura do chão. A sua energia potencial é joules, sendo , a aceleração da gravidade. Nesse lugar, como a bola está parada, a sua velocidade é igual a , e portanto a sua energia cinética também é igual a zero, ou seja . Assim, a sua energia mecânica total é . Ao ser lançada, essa bola atinge o solo e a sua altura ficará igual a , e consequentemente a sua . Como há conservação da energia mecânica, a energia cinética da bola no solo é . Deste valor podemos obter a componente escalar da velocidade instantes antes de a bola atingir o solo, ou seja . Quanto maior a altura de onde é lançada a bola, maior a velocidade atingida ao chegar ao solo. Vale também o contrário, isto é, quanto maior a velocidade, maior a altura atingida. Assim, se um atleta quiser saltar uma boa altura , é preciso correr muito para atingir uma velocidade alta. É isso que fazem os atletas que praticam salto em altura, salto tríplice e saltos com evoluções em ginástica olímpica.
Equações[editar | editar código-fonte]
A energia mecânica de um sistema conservativo é dada por:
- , a energia cinética;
- , a energia potencial.
Energia cinética[editar | editar código-fonte]
O trabalho feito por uma força ao longo de um caminho C é calculado pela seguinte integral:
Segundo o teorema do trabalho e da energia cinética:
Energia cinética de translação[editar | editar código-fonte]
A definição da energia cinética de translação é obtida mediante a resolução
da integral que define o trabalho:
- .
Usando a definição de força e a regra da cadeia, modifica-se o integrando e a variável de integração de modo a resolver a integral:
- ,
em que é o momento linear do objeto e é sua velocidade. Tomemos a definição de momento linear:
Diferenciando a expressão e a substituindo na integral:
Finalmente, resolve-se a integral:
Define-se a energia cinética, portanto, como:
O resultado da integração acima leva-nos à igualdade entre o trabalho e a variação da energia cinética:
Energia cinética de rotação[editar | editar código-fonte]
Energia potencial[editar | editar código-fonte]
Energia Potencial Gravitacional:
Energia Potencial Elástica:
Energia Potencial Elétrica:
Energia Potencial: Soma de todas as energias potenciais
Equações diferenciais[editar | editar código-fonte]
No formalismo que descreve a Mecânica, existem algumas equações diferenciais:
onde é o trabalho, a energia cinética e a energia potencial. No caso de a diferencial dW não ser exata, pode-se dizer que o trabalho W não depende do percurso.
Se a força é conservativa, resulta:
Dessa maneira, percebe-se que a energia mecânica não varia ao longo do "caminho".
Mecânica quântica[editar | editar código-fonte]
Tratando-se de física quântica, o formalismo dado à mecânica muda um pouco. As leis da física são vistas de maneira diferente no caso de uma escala próxima ao núcleo atómico. As equações que regem a dinâmica dos corpos (formalismo Hamiltoniano e Lagrangiano), são substituídas pela equação de Schrödinger:
onde é o operador Hamiltoniano, a função de onda e a energia do estado . É importante ressalvar que a equação de Schrödinger pode tomar a forma dependente e independente do tempo. Para isso, deve lembrar-se que:
Operador Hamiltoniana:
Operador momento:
Operador Potencial:
Energia: (no caso dependente do tempo)
Assim, no caso da equação independente do tempo, tem-se:
(equação independente do tempo)
Já no caso da dependente do tempo tem-se:
(equação dependente do tempo)
Exemplos[editar | editar código-fonte]
Nesta seção serão dados alguns exemplos do cálculo da energia mecânica.
Partícula livre[editar | editar código-fonte]
No caso de uma partícula livre, sabe-se que a energia potencial é nula. Assim, a energia mecânica é escrita como:
onde é o momento linear da partícula e sua massa.
Oscilador harmônico[editar | editar código-fonte]
No caso de uma partícula em um oscilador harmônico, a energia potencial pode ser escrita como:
com sendo a velocidade angular e a posição da partícula. Assim, a energia mecânica do sistema é dada por:
Atração gravitacional[editar | editar código-fonte]
No caso de uma partícula de massa em um potencial gravitacional gerado por outra partícula de massa , pode-se escrever a energia mecânica do sistema como
onde é a constante da gravitação universal e a distância entre os corpos.
Pêndulo simples[editar | editar código-fonte]
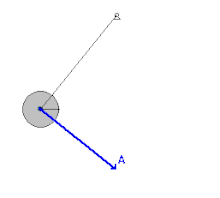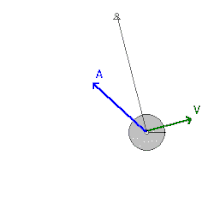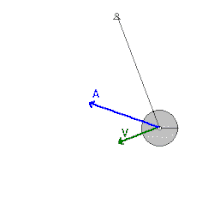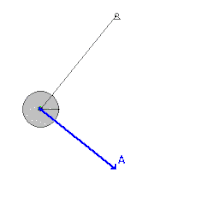
Em um pêndulo simples, a energia mecânica do sistema será igual à energia potencial gravitacional inicial, que é proporcional à altura da qual ele será solto. Durante o movimento de descida, a energia potencial converte-se continuamente em energia cinética devido ao trabalho realizado pela força gravitacional (peso). Quanto o corpo atinge o ponto mais baixo, toda a energia potencial foi transformada em cinética, correspondendo ao ponto de velocidade máxima do pêndulo. Uma vez passado esse ponto, o corpo começa sua subida e o processo inverso se inicia: a energia cinética se transformando em potencial gravitacional até que o corpo pare totalmente, na mesma altura em que foi solto do outro lado.
A energia mecânica do sistema de um pêndulo simples é dada pela expressão a seguir:
Em que é a energia potencial gravitacional e é a energia cinética associadas à massa do pêndulo. Pelo princípio da Conservação da Energia Mecânica, essa soma permanece constante ao longo do tempo, ou seja, quando a energia cinética aumenta, a potencial tem que diminuir e vice-versa.
Legenda[editar | editar código-fonte]
- =constante elástica
- =aceleração da gravidade (~9,81 m/s²) (constante)
- =energia cinética
- =massa (kg)
- =Momento de Inércia (kg*m²)
- (letra grega ômega) = velocidade angular (rad/s)
- =trabalho (J)
- =energia potencial gravitacional
- =energia potencial elétrica
- =energia potencial elástica
- =altura (m)
- =velocidade (m/s)
- =elongação ou deformação da mola









































































