Entalpia
Entalpia, por vezes referida como entalpia absoluta, é uma grandeza física definida no âmbito da termodinâmica clássica, de forma que esta meça a máxima energia de um sistema termodinâmico, teoricamente passível de ser deste removida na forma de calor. É particularmente útil na compreensão e descrição de processos isobáricos:[1] à pressão constante as variações de entalpia encontram-se diretamente associadas às energias recebidas pelo sistema na forma de calor, as quais são facilmente mensuráveis em calorímetros.
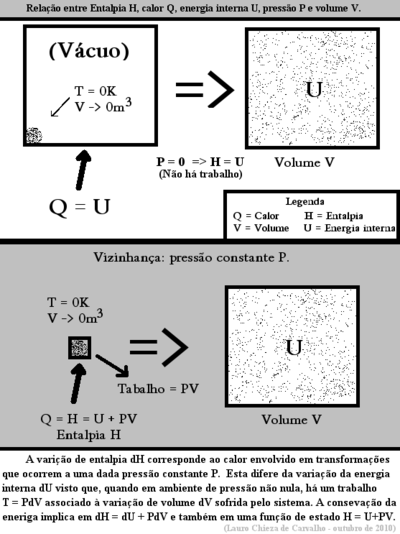
Conforme definida, a entalpia engloba em si não apenas a energia interna do sistema, mas também a energia armazenada no conjunto sistema-vizinhança que, absorvida pelo sistema via trabalho realizado pela vizinhança em processos termodinâmicos que impliquem a diminuição de seu volume, também integra uma parcela de energia passível de ser extraída na forma de calor a partir do referido sistema. A entalpia mensura pois a totalidade de energia de alguma forma atrelada ao sistema - incluindo-se nesta não apenas a energia encerrada no sistema como também a energia atrelada ao sistema em virtude das relações que este estabelece com a sua vizinhança.
Em acordo com o apresentado, a variação de entalpia, define-se por:[2][3]
onde U representa a energia interna do sistema e PV mensura a quantidade de energia associada ao conjunto sistema-vizinhança devido ao fato do sistema ocupar um volume V quando submetido à pressão constante P, ou seja, o máximo trabalho executável pela vizinhança sobre o sistema.
Embora as entalpias absolutas - assim como as energias internas absolutas - não desempenhem papel de maior relevância na análise prática de processos físico-químicos - sendo em verdade experimentalmente muito complicadas suas precisas determinações - as variações de entalpia são contudo facilmente mensuráveis via aparelhos conhecidos como calorímetros e estas sim desempenham papel o mais importante na análise dos citados processos. É a variação de entalpia em um dado processo termodinâmico - ou seja, a diferença entre as entalpias do estado final e do estado inicial visto ser a entalpia uma função de estado -, e não a entalpia em si, que retém real significado físico e prático: a variação de entalpia mensura o calor absorvido pelo sistema durante os processos termodinâmicos provido que estes realizem-se à pressão constante.
A entalpia-padrão de um sistema corresponde à entalpia do sistema antes descrita subtraída de uma constante adequadamente escolhida de forma a ter-se a entalpia-padrão de um sistema em particular - adequadamente escolhido para constituir um padrão universal de referência - propositalmente definida como zero. A definição de entalpia-padrão faz-se por razões práticas e não acarreta implicação alguma na determinação das variações de entalpia em processos termodinâmicos, visto serem as suas variações iguais às respectivas variações de entalpia absoluta (). Assim sendo, define-se de forma universalmente aceita que toda substância simples em estado padrão - ou seja, no estado físico e alotrópico mais estável, a 298,15 K (25°C) e 1 bar (100 000 Pa), tem entalpia-padrão por definição igual a zero - mesmo não sendo nula sua entalpia absoluta em tal estado. Determinar a entalpia-padrão de um estado particular de um sistema consiste pois em determinar a variação de entalpia em um processo qualquer que tenha por estado final o estado em consideração e que tenha por estado inicial sempre o estado padronizado associado. O estado inicial padrão constitui uma referência para a medida de entalpia, e a partir desta referência determinam-se doravante com facilidade as entalpias-padrão de todos os demais compostos químicos ou estados. Em particular, dá-se o nome de entalpia de formação à entalpia-padrão de uma substância pura composta; o que corresponde, dada a aplicação da definição de entalpia padrão ao caso, à variação de entalpia associada à reação que tem por estado inicial os elementos necessários à produção do composto - este em sua forma padrão - e por estado final apenas a substância composta em consideração - nas condições específicas à situação. As entapias-padrão das substâncias compostas - as entalpias de formação - são as entalpias que encontram-se geralmente tabeladas em livros e manuais, não raro figurando junto às variações de entalpias para reações químicas específicas.
No Sistema Internacional de Unidades a unidade da entalpia é o joule (J). Ao passo que na literatura a entalpia absoluta é geralmente representada pelo símbolo H, a entalpia-padrão encontra-se geralmente representada pelo símbolo H 0.
Quando expressa em função da entropia S, número de elementos N, e da pressão P - para o caso de sistemas termodinâmicos mais simples - a entalpia é, assim como o são as respectivas Transformadas de Legendre associadas, a saber a Energia livre de Helmholtz , a Energia livre de Gibbs e a energia interna , uma equação fundamental para os sistemas termodinâmicos em consideração. A partir de uma equação fundamental é possível via formalismo matemático inerente à termodinâmica obter-se qualquer informação física relevante para o sistema por ela descrito. Se a entalpia encontrar-se expressa em função de outras grandezas que não as mencionadas, esta constituirá apenas uma equação de estado e não em uma equação fundamental. Uma equação de estado não encerra em si todas as informações acerca do sistema; contudo a partir de todas as equações de estado do sistema é possível deduzir-se uma equação fundamental, e em consequência, via transformadas de Legendre, todas as demais.[4]
Definição[editar | editar código-fonte]
Quando um sistema imerso em um ambiente à pressão constante sofre um processo qualquer, indo de um estado inicial "i" para um estado final "f", a quantidade de energia trocada com a vizinhança na forma de trabalho é definida apenas pela variação de volume sofrida pelo sistema e pela pressão P do ambiente constate durante todo o processo. Assume-se aqui, sem perda de generalidade, que tem-se uma transformação quase-estática, de forma que a pressão P é também a pressão do sistema em si. A citada quantidade de trabalho W realizada pelo sistema sobre a vizinhança sob pressão constante é determinável através da expressão:
É de interesse mensurar neste tipo de transformação a quantidade de calor trocada entre o sistema e sua vizinhança. Ao ceder-se certa quantidade de calor ao sistema, este expande-se, realizando um trabalho W sobre a vizinhança. A energia entregue à vizinhança - e que por tal abandona o sistema - é transferida às custas de parte do calor que entra no sistema, de forma que apenas parte do calor transferido ao sistema implica real aumento na energia interna deste sistema. A lei da conservação da energia fornece:
Como a energia interna e o volume do sistema são funções de estado, segue-se que nestes processos a quantidade de calor trocada também é uma função de estado. A expressão acima permite a definição de uma grandeza física conhecida por entalpia H de forma que:
Decorre que a entalpia pode ser definida pela função de estado introduzida por Josiah Willard Gibbs:
Definição de Entalpia
onde U é a energia interna do sistema e PV é o produto da pressão pelo volume do sistema (e da vizinhança), ou seja, a energia armazenada no conjunto sistema vizinhança.
Conforme definida, a variação da entalpia implica pois a expressão antes apresentada para a conservação da energia:
A entalpia, por ser - assim como a energia interna e o trabalho - uma grandeza associada à medida de energia, é por tal também medida em joules.
É aqui importante ressaltar-se que a variação da entalpia em um dado processo corresponde sempre à entalpia do estado final menos a entalpia do estado inicial atrelados ao referido processo, e que em equações químicas esta corresponde pois a entalpia do estado onde tem-se os produtos menos a entalpia do estado onde tem-se os reagentes ().
Partindo-se do fato que a expressão da energia interna é uma equação fundamental para o sistema e assim o sendo encerra em si todas as informações acerca do comportamento deste, é de se esperar que seja possível, partindo-se desta expressão, inferir o comportamento do correspondente sistema à pressão constante, e por tal derivar-se da primeira a expressão para . Em acordo com o estabelecido pela Transformada de Legendre aplicada à energia interna , a fim de constituir também uma equação fundamental, a entalpia deve figurar em função, entre outras se houver, das grandezas extensivas entropia S, quantidade de matéria N, e da grandeza intensiva pressão P, devendo a correspondente grandeza extensiva conjugada à pressão - o volume V - ser substituída em mediante a relação:[5]
.
Caso a entalpia figure em função de demais grandezas que não as citadas, a exemplo em função da temperatura T ou mesmo do volume V, tal expressão não constituirá uma equação fundamental para o sistema, caracterizando-se então apenas como uma equação de estado.
A tabela que se segue apresenta os passos a serem seguidos a fim de se obter a entalpia a partir da energia interna , e vice versa mantidas as condições para que ambas figurem como equações fundamentais.
| Determinar e |
|---|
| Eliminação de U e V fornece: |
| Entalpia H |
| Determinar e |
|---|
| Eliminação de P e H fornece: |
| Energia Interna U |
- Exemplo
A equação fundamental para a Entalpia de um gás monoatômico ideal é, com sendo uma constante com dimensão adequado ao ajuste correto da análise dimensional:
Esta equação pode ser obtida a partir da equação fundamental para a energia interna seguindo-se os passos na parte superior da tabela apresentada, ou a partir dela pode-se obter a energia interna seguindo-se os passos na parte inferior da tabela em questão. Os cálculos associados são apresentados no artigo relacionado à Transformada de Legendre na presente enciclopédia. A título ilustrativo a energia interna para o sistema em questão expressa-se como:
A equação anterior pode facilmente ser reescrita a fim de tornar-se similar à encontrada em outros artigos da Wikipédia. Uma vez suprimidas constante(s) com unidade(s) definida(s) de forma a tornarem correta a análise dimensional,[7] esta apresentar-se-á como abaixo:
Variação de entalpia[editar | editar código-fonte]
A variação de entalpia () em transformações físico-químicas é geralmente expressa de forma proporcional à quantidade de matéria envolvida na reação, ou seja, proporcional ao número de mols envolvidos no processo. A exemplo, na reação termoquímica a seguir, a variação da entalpia (-241,2 kJ/mol) corresponde à variação de entalpia mensurada quando meio mol de reage com um mol de dando como resultado um mol de .
Quanto ao sinal do , observar-se-á que, em:
- Reações exotérmicas: . Há liberação de calor do sistema para a vizinhança.
- Reações endotérmicas: . Há uma absorção de calor pelo sistema.
As variações de entalpia em reações químicas podem ser mensuradas via medida do calor absorvido ou liberado na reação, sendo o procedimento experimentalmente levado a cabo em aparelhos conhecidos como calorímetros.
É importante mencionar que as variações de entalpia absoluta e entalpia padrão - esta definida como a entalpia absoluta menos uma constante C adequadamente escolhida (; ver próxima seção) - são iguais. Tal igualdade é facilmente demonstrável a partir da definição desta última:
assim, ao falar-se em variação, tanto faz falar-se da variação da entalpia-padrão ou falar-se da variação da entalpia absoluta. Fala-se pois simplesmente em variação de entalpia .
Entalpia, e entalpias[editar | editar código-fonte]
Em fundamento tem-se apenas uma entalpia, a antes definida entalpia absoluta - ou simplesmente entalpia. Contudo, dado um conjunto de situações específicas e similares, pode-se estabelecer "entalpias" também específicas ao conjunto, que não obstante carregam em seu nome a descrição da característica comum. Assim tem-se por exemplo a entalpia-padrão já discutida, a entalpia de formação, a entalpia de combustão, de vaporização, de dissolução, e quem sabe outras mais. Contudo todas[Nota 1] remontam, em essência e sem restrições, à definição inicial de entalpia absoluta - quando muito aparte alguma constante sem qualquer implicação prática - e à determinação das variações de entalpia ao longo dos processos que levam do estado inicial ao final. Assim, a "entalpia de combustão" nada mais é do que a variação de entalpia observada entre o estado inicial - neste caso definido como sendo um combustível + comburente - e o estado final - neste caso o produto da combustão, geralmente gás carbônico e água no caso da queima de hidrocarbonetos. As demais "entalpias" seguem o mesmo padrão.
Entalpia-padrão[editar | editar código-fonte]
Teoricamente, o cálculo do valor do só seria em princípio possível se fossem conhecidas as entalpias absolutas dos reagentes () e dos produtos () visto que . Tais valores absolutos, entretanto, são praticamente impossíveis de serem diretamente mensurados experimentalmente dado a utopia prática de um sistema de referência em um estado de entalpia absoluta zero. Na prática tem-se em verdade não há ganho ou obrigatoriedade alguma de que as entalpias a serem consideradas no cálculo sejam as entalpias absolutas dos estados do sistema. Tal consideração decorre do fato que, experimentalmente, com o uso do calorímetro, só é possível obterem-se os valores das variações devido às transformações do sistema visto que o calorímetro permite mensurar apenas o calor perdido ou recebido pelo sistema durante uma dada transformação, mas não a energia interna e a energia associada ao volume sob pressão de um estado particular do sistema. As variações de entalpia correspondem pois às grandezas experimentalmente mesuráveis e de relevância.
Em vista da situação há pois uma liberdade de escolha quanto ao "nível" de referência ao qual associar-se-á por definição um valor de entalpia nulo visto que não há razão prática alguma que acarrete a necessidade da entalpia "zero" encontrar-se obrigatoriamente associada - como encontra-se na definição de entalpia absoluta - a um estado do sistema à temperatura de zero kelvins e cujos volume e energia interna clássicos sejam nulos - ou seja, ao estado naturalmente determinado para o qual a entalpia absoluta é nula. De forma similar ao que ocorre com a determinação de diferenças de alturas, onde o valor obtido para a espessura ("altura") de uma mesa - ou seja, a diferenças de alturas entre o topo e o pé da mesa - independe do nível de referência escolhido para medirem-se as alturas a serem subtraídas - podendo estas serem medidas tanto em relação o piso da sala como em relação o nível do mar sem contudo afetar-se o resultado de interesse prático - pode-se em princípio também escolher um nível de referência qualquer a partir do qual as entalpias serão mensuradas e a partir dos quais as variações de entalpia sejam sempre corretamente determináveis.
Embora a escolha do "nível" de referência seja em princípio livre, é extremamente valioso que este estabeleça-se um padrão experimentalmente bem definido e que seja por todos facilmente reprodutível e universalmente reconhecido, de forma a permitir a fácil determinação dos valores de entalpia para as mais variadas substâncias puras compostas visto que isso certamente facilitará muito o cálculo teórico do nas milhares de transformações químicas existentes bem como o intercâmbio de dados e resultados práticos entre profissionais dos mais diversificados ramos de atividade pertinentes. A fim de estabelecer tal nível de referência padrão determinaram-se primeiramente, entre outros, as condições físico-químicas de referência para os quais a entalpia - esta doravante nomeada entalpia-padrão - será definida como zero. Convencionou-se, entre outros, que constituir-se-á o sistema de referência por todas as substâncias simples, e que o estado padrão será o estado físico e alotrópico mais estável destas substâncias à temperatura de 25 °C e pressão de 1 atm.. A partir desta definição, mensurada a variação de entalpia em qualquer processo que leve o sistema das condições de referência - a justaposição para reação da mistura de substâncias simples - a um estado final em particular - a substância composta formada - foi e é possível determinar-se a entalpia-padrão associada a qualquer estado final desejado, e de forma recorrente, as entalpias-padrão e variações de entalpia para as mais diversas reações, mesmo para aquelas envolvendo várias substâncias puras ou mesmo compostas atuando tanto como reagentes quanto como produtos. Tais entalpias-padrão, ou suas variações - cujos valores coincidem com as variações de entalpia absoluta - encontram-se desta forma tabeladas em muitos livros de química e física para as mais diversas substâncias e reações químicas.
Tem-se pois que pela definição as entalpias-padrão do hidrogênio (), do oxigênio () ou do grafite (C) quando nas condições padrão, ou seja, a 25 °C de temperatura e 1 atm. de pressão, são por definição, zero. O mesmo já não ocorre para o diamante (carbono em estado alotrópico menos estável), (substância composta) e outras, mesmo que nas condições padrão de temperatura e pressão.
É conveniente explicitar-se que, conforme definidas, a entalpia absoluta e a entalpia-padrão diferem entre si por uma mera subtração de um valor adequadamente escolhido para cada situação:
onde C representa uma constante.
Uma vez estabelecido o padrão de referência e uma forma de mensurarem-se as entalpias-padrão dos sistemas nos seus diversos estados, mostra-se também válido estabelecer alguns conceitos de utilidade prática derivados, a exemplo os conceitos de entalpias de formação e de entalpia de combustão das substâncias.
Entalpia de formação[editar | editar código-fonte]
Refere-se à energia liberada ou absorvida quando um mol de um composto se forma a partir de substâncias simples no estado padrão - as quais têm entalpia-padrão por definição igual a zero.[9]
Exemplo:
A equação acima indica que a entalpia de formação do etanol :, é igual a -277,7 kJ. Repare que a reação é exotérmica: energia é liberada na formação de etanol a partir das substâncias simples associadas.
Entalpia de combustão[editar | editar código-fonte]
Refere-se à energia liberada na combustão de um mol de um composto; desde que todos os participantes da reação estejam no estado-padrão.
Exemplo:
A equação acima indica que a entalpia de combustão do metano :, é igual a -889,5 kJ. Assim como o que se observa na reação de formação do metano, a reação de combustão do metano também é exotérmica.
Entalpia de ligação[editar | editar código-fonte]
Outra forma de calcular a variação de entalpia de uma reação química envolve o conceito de energias de ligação, ou seja, aquela relacionada à variação da energia potencial associada à força que une os átomos: entalpia de ligação é a energia necessária para romper um mol de ligações químicas entre pares de átomos no estado gasoso.
É importante ressaltar que a entalpia de ligação será sempre positiva visto que, pela definição, a exemplo do hidrogênio, tem-se a seguinte ordem entre reagente e produto:
e não o contrário
(incorreto) .
Considerando que a quebra de ligações é um processo endotérmico, e que a formação de ligações é um processo exotérmico, uma forma prática de calcular-se o de uma reação química é a partir dos valores de energia liberada na quebra de ligações e absorvida na formação de novas ligações. Para tanto, faz-se necessário conhecer as entalpias de ligação para cada ligação específica entre cada par de átomos específico. Calcula-se, então, a variação de entalpia pela diferença entre as entalpias de ligação das ligações rompidas e as entalpias de ligação das ligações formadas.[10] Contudo é demonstrável que este método fornece resultados mais para aproximados do que para exatos visto que a energia de uma dada ligação é influenciada pela existência ou não bem como pela natureza das demais ligações sendo realizadas por um ou mesmo pelo par de átomos em consideração. Verifica-se que, por razões práticas, as entalpias de ligação associadas a uma dada ligação refletem em verdade uma média para as diversas situações tipicamente encontradas. Um tratamento via entalpias de ligação de um dado átomo a grupos termoquímicos específicos melhora a situação mas não remove completamente a imprecisão .[11]
Encontram-se com facilidade na literatura tabelas contendo as entalpias de ligação para as mais variadas ligações. A partir das mesmas é possível fazer-se uma estimativa das variações de entalpia em processos envolvendo reagentes e produtos definidos por tais ligações. A exemplo, pode-se determinar a variação de entalpia associada à reação (∆H=?):
uma vez conhecidos as entalpias de ligação:[12]
| C–H | +413,4 KJ/mol |
| O=O | +468,6 KJ/mol |
| C=O | +804,3 KJ/mol (para CO2) |
| H–O | +463,5 KJ/mol |
Vistos que todos os elementos encontram-se no estado gasoso, assumidos nas condições normais de temperatura e pressão, pode-se determinar a requisitada variação de entalpia, que corresponde à entalpia do estado final (produtos) menos a entalpia do estado inicial (reagentes) de duas maneiras:[13]
1) Pela diferença entre as entalpias de formação ∆H 0F (= H0F) dos produtos e dos reagentes.
2) Pela diferença entre as entalpias de ligação ∆HL (= HL) das ligações rompidas e das ligações formadas.
Como dispõe-se das entalpias de ligação, sendo este o caso em consideração, aplicar-se-á a regra 2. Tem-se assim:
a) Ligações a serem quebradas: 4 mols de ligações C-H para desfazer-se o metano, 2 mols de ligações O=O para desfazerem-se os dois mols de O2.
Tem-se que a soma das entalpias de ligação para as ligações a serem quebradas vale:
= 4 mols * (+413,4 KJ/mol) + 2 * + (468,6 KJ/mol) = 2 590,8 KJ
b) Ligações a serem formadas: 2 mols de ligações C=O formam 1 mol de CO2 ; 4 mols de ligações H-O formando 2 mols de H2O.
Tem-se que a soma das entalpias de ligação associadas às ligações que serão formadas vale:
A variação de entalpia para a reação inicial de combustão do metano vale, segundo a regra 2, a diferença entre as entalpias de ligação quebradas [], cuja soma foi determinada no caso (a), e as entalpias de ligações formadas [], cuja soma foi determinada em (b). Tem-se pois que:
= 2 590,8 KJ – 3 462,6 KJ = - 871,8 KJ
de onde
A reação é exotérmica visto que a variação de entalpia é negativa, conforme esperado por se tratar da combustão do metano, e libera aproximadamente 871,8 KJ de energia via calor. A entalpia do estado final é cerca de 871,8 KJ menor do que a entalpia do estado inicial.
Entendendo os cálculos[editar | editar código-fonte]
O mecanismo em questão para o cálculo de , conforme apresentado, deriva, em verdade, da aplicação da lei de Hess (ver seção a frente) a um conjunto de reações: para o presente exemplo, o primeiro somatório corresponde a uma variação de entalpia associada à seguinte reação:
Em uma segunda etapa tem-se a reação:
cuja variação de entalpia é determinada pelo negativo do segundo somatório (-Σ HL(formadas)), visto que as ligações são agora formadas e não quebradas.
Trata-se assim da decomposição da reação original em duas etapas levada a cabo via inserção de um estado intermediário contendo elementos não ligados. Conforme esperado pelo fato da entalpia ser função de estado, a variação de entalpia total será a soma das variações de entalpia associadas a cada etapa da reação, o que leva corretamente, conforme esperado, a:
Entalpia de ligação ou energia de ligação?[editar | editar código-fonte]
Uma vez resolvido o problema conforme apresentado, de grande importância perceber que, embora seja verdade que para determinarem-se as ligações a serem rompidas deva-se olhar sobretudo para o lado da equação correspondente aos reagentes, e que para determinarem-se as reações a serem feitas deva-se olha prioritariamente para o lado da equação correspondente aos produtos, a primeira somatória acima (a soma das entalpias de ligação para as ligações quebradas,(Σ HL(rompidas)), não é um cálculo que fornece por resultado a entalpia HR - quer absoluta, quer padrão, quer em relação a qualquer nível pré-estabelecido - do estado inicial (dos reagentes), ou seja, esta expressão não representa o cálculo da entalpia do estado do sistema antes da reação; e que a segunda somatória em questão, (Σ HL(formadas)), não é um cálculo válido acerca da determinação da entalpia do estado final HP - quer absoluta, quer padrão, quer em relação a qualquer nível pré-estabelecido - ou seja, do estado associado aos produtos da reação, quando já formados. A equação acima, por tal, não implica que esteja-se a fazer, a fim de determinar-se a variação de entalpia ∆H na combustão do metano, “a diferença de entalpias dos reagentes e dos produtos (HR – HP)”, pois não se está a determinar, com cada parcela da mesma, a entalpia dos reagentes, HR, e dos produtos, HP. Em verdade o cálculo acima, após concluído, configura uma forma alternativa de determinar-se a variação da entalpia associada à reação, ou seja, uma forma alternativa ao método tradicional onde faz-se - por definição de variação - o valor da entalpia do estado final – dos produtos - menos a entalpia do estado inicial – dos reagentes.
Escreve-se corretamente pois que:
(correto)
e não que
(incorreto) .
Poder-se-ia em princípio, contudo, a fim de evitar-se confusão certa quanto a não diferenciação explicita do "H" que figura ante e dos "H" que figuram depois do sinal de igual na sentença anterior - e eles são diferentes, o primeiro representando a entalpia do sistema e os demais entalpias de ligação - argumentar que embora a expressão anterior não encontre-se escrita de forma correta, para uma dada reação qualquer esta contudo seria valida:
(inadequado, embora "aceita" por alguns autores)
O problema com esta notação reside em um ponto bem simples: a ausência de referencial padrão teórico e experimentalmente válio para a medida da "entalpia de ligação" a ser adotado em sua definição, ou seja, na tentativa de definir-se uma nova função de estado para o sistema a ser nomeada "entalpia de ligação" .
Não há dúvidas que a entalpia de ligação e tradicional devam ser definidas de formas distintas visto que, dados o estado inicial e o estado final do sistema, o intuito é definir a entalpia de ligação de forma que um aumento em seu valor ( implique necessariamente, conforme equação em parágrafo anterior, uma diminuição da entalpia padrão (), raciocínio pertinente visto que energia presa em uma ligação é energia que não pode ser transferida na forma de calor.
Em hipótese a opção para referencial seria o estado intermediário inserido no processo a fim de suportar o raciocínio sendo considerado, ou seja, seria o estado de referência um estado onde encontrar-se-iam apenas elementos isolados - desprovidos de qualquer ligação. Definir-se a “entalpia de ligação” deste estado como zero, e por conseguinte, a entalpia de ligação de um estado em particular seria definida, em acordo com a situação, como o negativo da variação de entalpia (tradicional) associada à formação de um elemento via estabelecimento de ligações entre os átomos avulsos em questão. Ter-se-ia pois a entalpia de ligação sempre positiva, e que
Ressalta-se que tal definição - que tenta ser condizente com a real definição de entalpia de ligação - seria contudo apenas complicadora, visto que o estado contendo apenas átomos sem ligação, excetuado gases nobres, é experimentalmente muito mais inacessível do que um sistema contendo elementos em estado padrão, e de forma mais inquietante, que este estado, tipicamente embora não necessariamente, implica um estado do sistema fora de seu equilíbrio termodinâmico. E para estados fora do equilíbrio não se definem os potenciais termodinâmicos, a exemplo, uma entalpia.
Grosso modo, fazê-lo seria pois apenas - a menos de um sinal - dar nova definição à “entalpia-padrão” - mediante mudança do nível de referência - de forma a apenas, em princípio, complicá-la teórica e experimentalmente.
Da forma que a entalpia de ligação é realmente definida - alguns autores mencionam apenas energia de ligação talvez por esta razão - a entalpia de ligação não é propriedade de um estado em particular e sim uma propriedade de um processo em específico onde há quebra de determinada ligação em particular, e em verdade, de forma mais detalhada - onde há a quebra de ligação entre um radical e um elemento em particular. A proposta de notação
(inadequado, embora "aceita" por alguns autores)
é por tal, inadequada: busca expressar um raciocínio válido (a lei de Hess), contudo de forma infeliz.
Confirma-se tal afirmação observando que, embora uma variação na entalpia de ligação implique realmente uma variação na entalpia-padrão do sistema, há diversos processos que implicam uma variação da entalpia-padrão do sistema sem que contudo estes impliquem uma variação na energia de ligação de seus componentes. A associação conforme feita seria, pois, de mão única.
A alternativa para expressar-se o que realmente ocorre é definir-se uma energia de ligação - a nomear-se aqui por EL de forma a nitidamente dissociar o conceito de energia de ligação do conceito de entalpia e conectá-lo ao conceito de calor de reação, e afirmar que variações na energia de ligação, quando presentes, implicam variações correspondentes na entalpia do sistema determináveis segundo a expressão:
(correto) .
Não sendo a energia de ligação promovida ao status ou uma mera re-expressão de um potencial termodinâmico do sistema, portanto.
Entalpia de dissolução[editar | editar código-fonte]
A dissolução de uma substância em água - principalmente para o caso das substâncias iônicas - ocorre sempre com transferência de energia. Uma vez verificado que a maioria das reações químicas se processa em meio aquoso, a compreensão acerca da entalpia de dissolução mostra-se importante à correta análise de tais processos.
Define-se a entalpia de dissolução como a variação de entalpia associada à dissolução de 1 mol de soluto em uma quantidade de solvente maior ou igual à mínima necessária para que se tenha a máxima variação de entalpia no processo, ou seja, para que se tenha a dissolução completa do soluto.
Um típico processo onde a entalpia de dissolução pode ser facilmente evidenciada refere-se à dissolução em água do vulgo "percloreto de ferro" - corretamente cloreto férrico - frequentemente realizada por profissionais ou amantes de eletrônica a fim de se obter uma solução adequadamente diluída de forma a poder ser utilizada no processo de corrosão de placas de circuito impresso - placas de material isolante com uma fina camada de cobre em sua superfície -, placas estas sobre as quais primeiro desenham-se e posteriormente à corrosão montam-se os circuitos eletrônicos projetados. A dissolução deve ser feita vagarosamente tamanho é o aquecimento que a mesma provoca, sempre jogando-se o percloreto na água, e nunca o contrário. A entalpia de dissolução para tal produto é consideravelmente alta em módulo - contudo negativa em valor, visto que a dissolução é exotérmica.
Dependendo do espécime químico o processo de dissolução pode em si não ser muito simples, por vezes incluindo várias etapas, as quais podem implicar respectivas variações de entalpia com sinais trocados. A exemplo, durante a dissolução de sólido iônico típico em água, em uma primeira etapa o cristal iônico é desfeito, e tal dissolução requer energia, implicando que a etapa é endotérmica (. Em uma segunda etapa cada um dos íons passa a ser circundado por um número adequado de moléculas de água devidamente orientadas - processo conhecido como hidratação das partículas - o qual é acompanhado de uma considerável liberação de energia, sendo por tal um processo exotérmico que acarreta uma significativa diminuição da entalpia ().[10]O valor total da entalpia de dissolução depende então de qual das partes irá predominar. Extrapolando o conceito, a exemplo, ao contrário da dissolução de percloreto em água, a "dissolução" do sal de cozinha quando misturado com gelo mostra-se consideravelmente endotérmica.
Entalpia de vaporização[editar | editar código-fonte]
A entalpia de vaporização ou calor de vaporização é a quantidade de energia necessária para que um mol de um elemento ou de uma substância que encontre-se em equilíbrio com o seu próprio vapor passe completamente para o estado gasoso. Supõe-se a pressão constante, por padrão 1 atmosfera ou em caso contrário conforme explicitamente especificada. Mais informações, e tabela de valores para as substâncias típicas encontram-se disponíveis no artigo especialmente destinado ao assunto nesta enciclopédia eletrônica.
Entalpia de fusão[editar | editar código-fonte]
A entalpia de fusão ou calor de fusão é a quantidade de energia necessária para que um mol de um elemento ou substância em equilíbrio com seu líquido passe do estado sólido para o estado líquido mantida a pressão constante, usualmente definida como 1 atmosfera, ou conforme explicitamente especificada, em caso contrário.
Mais informações encontram-se disponíveis no artigo especialmente destinado ao assunto nesta enciclopédia eletrônica.
Processos endotérmicos, exotérmicos, e espontaneidade[editar | editar código-fonte]
O processo endotérmico é aquele que ocorre com absorção de energia na forma de calor pelo sistema. Um exemplo disso: se um pedaço de gelo for deixado sobre a mesa à temperatura ambiente, ele receberá energia na forma de calor do ambiente e isso provocará a fusão do gelo. A transição da água no estado sólido para o estado líquido é um processo em que há calor da vizinhança para o sistema, ou seja, é endotérmica.
Outro exemplo: quando um mol de óxido de mercúrio sólido se decompõe, à pressão constante, em um mol de mercúrio líquido e meio mol de oxigênio gasoso, ocorre a absorção de 90,7 kJ de energia do ambiente. Matematicamente:
Que também pode ser representada por:
O processo exotérmico é aquele que ocorre com liberação de energia na forma de calor para a vizinhança. Pode-se citar o seguinte como exemplo: quando um sistema formado por água líquida é colocado em um congelador, ele perde energia na forma de calor para esse ambiente e, em decorrência disso, ocorre a solidificação da água. Assim, transição da água no estado líquido para o estado sólido é um processo em que há calor do sistema para a vizinhança: é exotérmico.
Outro exemplo: quando um mol de hidrogênio gasoso reage, à pressão constante, com meio mol de oxigênio gasoso para formar um mol de água líquida, ocorre a liberação de 285,8 kJ de energia para o meio ambiente. Matematicamente:
Que também pode ser representada por:
Repare a correspondência entre os sinais das respectivas variações nas entalpias-padrão e a natureza da reação. Em reações exotérmicas há calor do sistema para a vizinhança, o que implica que a entalpia final do sistema é sempre menor do que a inicial; a diferença será sempre negativa visto que implica . Raciocínio análogo acarreta que em reações endotérmicas a entalpia final é maior do que a inicial, e a diferença será sempre positiva em reações endotérmicas visto que implica .
Relevante ao contexto é a falsa afirmação de que reações exotérmicas () são espontâneas, e endotérmica ()não são espontâneas. A reação entre gelo e sal de cozinha é endotérmica, contudo espontânea. Embora verdade para um grande número de situações, não é difícil encontrarem-se situações onde tal afirmação falha drasticamente. Em condições ambientes o que determina a espontaneidade de uma reação ou processo não é o sinal da variação da entalpia no processo e sim o sinal da variação da energia livre de Gibbs no processo a ser desencadeado.
Fatores que influenciam o valor da variação de entalpia[editar | editar código-fonte]
- Quantidade de reagentes e produtos: o valor do de uma reação varia em função da concentração de cada um de seus participantes. O aumento da concentração provoca um aumento proporcional da variação de entalpia.
Exemplo:
- Os estados físicos dos reagentes e produtos: substâncias no estado sólido provocam variações de entalpia maiores do que no estado líquido; e estas, maiores do que no estado gasoso.
Exemplo:
- Estado alotrópico de reagentes e produtos: cada estado alotrópico tem um valor de entalpia distinto.
Exemplo:
- Temperatura.
Uma reação exoenergética em uma dada temperatura pode mostrar-se endoenergética em outra temperatura, de forma que as temperaturas dos reagentes e produtos devem — quando fora do padrão — ser especificadas.
Lei de Hess[editar | editar código-fonte]
Em 1840, um físico chamado Germain Henry Hess, com base em seus estudos sobre calores de reação, descobriu que, de um modo geral, quando uma reação se dá em etapas, a soma dos calores de reação correspondentes aos diversos estágios é igual ao calor de reação obtido quando a reação é realizada completamente em uma só etapa.
Então, enunciou sua lei: "Quando uma reação química apresenta etapas intermediárias, a variação de entalpia da reação geral equivale à soma das variações de entalpia de cada uma das etapas intermediárias". A lei de Hess implica a verificação experimental de que a entalpia é uma função de estado, ou seja, de que a variação da entalpia depende em um sistema depende apenas dos estados inicial e final do sistema - sendo sempre determinável pela diferença - isto de forma independente de como o sistema evoluiu do estado inicial "i" para o estado final "f". Dados os mesmos estados inicial e final a variação de entalpia total observada será sempre a mesma, quer a reação se dê por etapas, quer se dê via uma única etapa, quer rápida, quer lentamente.
Podemos utilizar como exemplo simples da aplicação da Lei de Hess a reação de oxidação do carbono. É possível que o carbono se combine com um único átomo de oxigênio, formando o monóxido de carbono:
O monóxido de carbono é combustível, isto é, ele pode se combinar com outro átomo de oxigênio, produzindo dióxido de carbono; por este motivo, ocorre a reação de combustão:
Se somarmos estas duas equações (como se elas fossem equações algébricas), poderíamos também, segundo a Lei de Hess, somar as entalpias de reação:
Continuando a utilizar regras análogas às empregadas na álgebra, podemos eliminar todos os elementos que aparecem nos dois membros da equação - neste caso, eliminamos o .
Somando e , podemos anotar 1 mol deste gás, e o resultado final será:
que é exatamente a entalpia da reação se queimássemos diretamente o carbono a dióxido de carbono.
Notas
- ↑ A "entalpia de ligação" apresenta algumas particularidades próprias.
Referências
- ↑ Assume-se o sistema em equilíbrio mecânico com sua vizinhança, ou seja, que as pressões do sistema e da vizinhança sejam sempre iguais.
- ↑ «Oxford Living Dictionaries». Consultado em 19 de fevereiro de 2018. Cópia arquivada em 17 de agosto de 2016
- ↑ «IUPAC Gold Book. Enthalpy, H». Consultado em 19 de fevereiro de 2018
- ↑ Em acordo com Callen, Herbert B. - Thermodynamics and An Introduction to Thermostatics - John Wiley & Sons - ISBN 0-471-86256-8
- ↑ Callen, Herbert B. - Thermodynamics and an Introduction to Thermostatics - John Wiley & Sons - 1985 - ISBN 0-471-86256-8
- ↑ Ambas as expressões, H e U, conforme artigo sobre Gás Ideal na wikipédia lusófona, conforme publicado em 10 março 2010 às 19:06.]]
- ↑ A saber, o expoente em funções exponenciais e o logaritmando em logaritmos devem ser adimensionais.
- ↑ Conforme Salinas, Silvio R. A. - Introdução à Física Estatística - EdUSP - 1999 - ISBN 85-314-0386-3
- ↑ «Entalpia padrão de formação». - www.unb.br
- ↑ a b Nóbrega, Olímpio Salgado ; Roberto da Silva, Eduardo ; Hashimoto da Silva, Ruth - Química - Volume único - editora Ática - São Paulo - 2008 - ISBN 978-85-08-11059-9
- ↑ Atkins - Fisico-química.
- ↑ Mortimer, Eduardo Fleury at al. - Química para o ensino médio – Editora Scipione – ISBN 85-262-4456-6
- ↑ Nobrega, Olimpio Salgado; at al. - Química – Volume único – ISBN 978-85-08-11059-9, Pág. 435
Ver também[editar | editar código-fonte]
- Entalpia de combustão
- Trocador de calor
- Unidade de recuperação de calor
- Arrefecimento gratuito
- Entropia
Ligações externas[editar | editar código-fonte]
- ENTALPIA- educar.sc.usp.br - Uma abordagem simples e didática sobre entalpia.
- José Luis de Paula Barros Silva; Por que não estudar entalpia no Ensino Médio; QUÍMICA NOVA NA ESCOLA; N° 22, NOVEMBRO 2005































![{\displaystyle H(S,P,N)={\frac {5}{2}}Nk\left(P\Phi \,e^{[({\frac {S}{Nk}}-c)-{\frac {5}{2}}]}\right)^{\frac {2}{5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9804bb5921b121117cc9af3a325e91b827da7a3)

![{\displaystyle U_{(S,V,N)}=N({\frac {N}{V}})^{\frac {2}{3}}e^{[{\frac {2}{3}}({\frac {S}{Nk_{B}}}-c)]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12cc8927c7289a257629d531b8232a6007cb92c7)





































![{\displaystyle \Delta H=[H_{R}]-[H_{P}]\;\;\;\;(=[\Sigma H_{(rompidas)}^{L}]-[\Sigma H_{(formadas)}^{L}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12f4197eca734805681d14a68f3c7fc4dbfbc5e5)
![{\displaystyle \Delta H=[H_{R}^{L}]-[H_{P}^{L}]=-\Delta H^{L}\;\;\;\;(=[\Sigma H_{(rompidas)}^{L}]-[\Sigma H_{(formadas)}^{L}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/433c00ff33e3c96033edba97961691a3fd79820e)





![{\displaystyle \Delta E^{L}=>\Delta H=H_{P}-H_{R}=[\Sigma H_{(rompidas)}^{L}]-[\Sigma H_{(formadas)}^{L}]=[E_{R}]-[E_{P}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47a963d6fd4be764ba0189d291e00f5ee8589c34)



















