Relatividade geral
Relatividade geral, também conhecida como teoria da relatividade geral, é uma teoria geométrica da gravitação publicada por Albert Einstein em 1915 e a descrição atual da gravitação na física moderna. É um conjunto de hipóteses que generaliza a relatividade especial e a lei da gravitação universal de Newton, fornecendo uma descrição unificada da gravidade como uma propriedade geométrica do espaço e do tempo, ou espaço-tempo. Em particular, a "curvatura do espaço-tempo" está diretamente relacionada à energia e ao momento de qualquer matéria e radiação presente. A relação é especificada pelas equações de campo de Einstein, um sistema de equações diferenciais parciais.
Muitas previsões da relatividade geral diferem significativamente das da física clássica, especialmente no que respeita à passagem do tempo, a geometria do espaço, o movimento dos corpos em queda livre, e a propagação da luz. Exemplos de tais diferenças incluem a dilatação do tempo gravitacional, lente gravitacional, o desvio gravitacional para o vermelho da luz, e o tempo de atraso gravitacional. Previsões da relatividade geral foram confirmadas em todas as observações e experimentos até o presente. Embora a relatividade geral não seja a única teoria relativística da gravidade, é a mais simples das teorias que são consistentes com dados experimentais. No entanto, há questões ainda sem resposta, sendo a mais fundamental delas explicar como a relatividade geral pode ser conciliada com as leis da física quântica para produzir uma teoria completa e auto-consistente da gravitação quântica.
A teoria de Einstein tem importantes implicações astrofísicas. Ela aponta para a existência de buracos negros — regiões no espaço onde o espaço e o tempo são distorcidos de tal forma que nada, nem mesmo a luz, pode escapar — como um estado final para estrelas maciças. Há evidências de que esses buracos negros estelares, bem como outras variedades maciças de buracos negros são responsáveis pela intensa radiação emitida por certos tipos de objetos astronômicos, tais como núcleos ativos de galáxias ou microquasares. O desvio da luz pela gravidade pode levar ao fenômeno de lente gravitacional, onde várias imagens do mesmo objeto astronômico distante são visíveis no céu. A relatividade geral também prevê a existência de ondas gravitacionais, que já foram medidas indiretamente; uma medida direta, no final de 2015, por pesquisadores do projeto LIGO (Observatório de Ondas Gravitacionais por Interferômetro Laser) confirmou as "distorções no espaço e no tempo" causadas por um par de buracos negros com 30 massas solares em processo de fusão. Além disso, a relatividade geral é a base dos atuais modelos cosmológicos de um universo em expansão.
Amplamente reconhecida como uma teoria de grande beleza matemática, a relatividade geral tem sido frequentemente descrita como a mais bela de todas as teorias físicas existentes.[2]
História[editar | editar código-fonte]
Logo depois de publicar a teoria da relatividade especial em 1905, Einstein começou a pensar sobre como incorporar a gravidade em sua nova estrutura relativista. Em 1907, começando com um simples experimento mental envolvendo um observador em queda livre, embarcou no que seria uma busca de oito anos por uma teoria relativística da gravidade. Após inúmeros desvios e falsos começos, seu trabalho culminou na apresentação à Academia de Ciências da Prússia, em novembro de 1915, do que hoje são conhecidas como as equações de campo de Einstein, que formam o núcleo da teoria geral da relatividade.[3] Essas equações especificam como a geometria do espaço e do tempo é influenciada por qualquer matéria e radiação presentes.[4]

As equações de campo de Einstein são não-lineares e consideradas difíceis de solucionar. Einstein usou métodos de aproximação na elaboração das previsões iniciais da teoria. Mas em 1916, o astrofísico Karl Schwarzschild encontrou a primeira solução não trivial exata para as equações de campo, a métrica de Schwarzschild. Esta solução estabeleceu as bases para a descrição das etapas finais do colapso gravitacional e os objetos conhecidos hoje como buracos negros. No mesmo ano, foram realizados os primeiros passos para a generalização da métrica de Schwarzschild para objetos carregados eletricamente, o que acabou resultando na métrica de Reissner-Nordström, agora associada a buracos negros carregados eletricamente.[5] No ano seguinte, Einstein aplicou sua teoria ao universo como um todo, iniciando o campo da cosmologia relativista. Em consonância com o pensamento contemporâneo, assumiu um universo estático, adicionando um novo parâmetro às suas equações de campo originais — a constante cosmológica — para combinar com essa presunção observacional.[6] Em 1929, no entanto, o trabalho de Edwin Powell Hubble e outros mostrava que o nosso universo está se expandindo. Isto é prontamente descrito pelas soluções cosmológicas em expansão encontradas por Alexander Friedmann em 1922, que não exigem uma constante cosmológica. Georges Lemaître usou essas soluções para formular a versão mais antiga dos modelos do Big Bang, em que nosso universo evoluiu a partir de um estado anterior extremamente quente e denso.[7] Einstein declarou mais tarde a constante cosmológica como o maior erro de sua vida.[8]
Durante esse período, a relatividade geral permaneceu como uma curiosidade entre as teorias físicas. Era claramente superior à gravidade newtoniana, sendo consistente com a relatividade especial e contabilizando vários efeitos inexplicados pela teoria clássica. O próprio Einstein havia mostrado em 1915 como sua teoria explicava a precessão anormal do periélio do planeta Mercúrio sem quaisquer parâmetros arbitrários ("fatores de correção").[9] Da mesma forma, uma expedição de 1919 liderada por Arthur Stanley Eddington confirmou a previsão da relatividade geral para a deflexão da luz das estrelas pelo Sol durante o eclipse solar total de 29 de maio,[10] tornando Einstein instantaneamente famoso.[11] No entanto, a teoria tornou-se consolidada na física teórica e na astrofísica apenas com os desenvolvimentos por volta de 1960 e 1975, hoje conhecidos como a era dourada da relatividade geral.[12] Físicos começaram a entender o conceito de buraco negro e a identificar quasares como uma das manifestações astrofísicas desses objetos.[13] Testes cada vez mais precisos com o sistema solar confirmaram o poder preditivo teórico,[14] e a cosmologia relativística também se tornou passível de testes de observação direta.[15]
Da mecânica clássica à relatividade geral[editar | editar código-fonte]
A relatividade geral pode ser entendida examinando suas semelhanças e desvios da física clássica. O primeiro passo é a compreensão de que a mecânica clássica e a lei da gravidade de Newton admitem uma descrição geométrica. A combinação dessa descrição com as leis da relatividade especial resulta em uma derivação heurística da relatividade geral.[16]
Princípio da Relatividade Geral[editar | editar código-fonte]

Na base da mecânica clássica está a noção de que o movimento de um corpo pode ser descrito como uma combinação de movimento livre (ou inercial) e desvios desse movimento. Tais desvios são causados por forças externas que agem sobre um corpo de acordo com a segunda lei de Newton, que afirma que a força resultante que atua sobre um corpo é igual à massa desse corpo (inercial) multiplicada por sua aceleração.[17] Os movimentos inerciais preferidos estão relacionados à geometria do espaço e do tempo: nos referenciais padrões da mecânica clássica, objetos em movimento livre se movem ao longo de linhas retas em velocidade constante. Na linguagem moderna, seus caminhos são geodésicos, linhas de universo retas no espaço-tempo curvo.[18]
Por outro lado, pode-se esperar que os movimentos inerciais, uma vez identificados observando os movimentos reais dos corpos e fazendo concessões para as forças externas (como eletromagnetismo ou atrito), possam ser usados para definir a geometria do espaço, bem como uma coordenada de tempo. No entanto, existe uma ambiguidade, uma vez que a gravidade entra em jogo. De acordo com a lei da gravidade de Newton, e verificada independentemente por experimentos como o de Eötvös e seus sucessores (veja experimento de Eötvös), há uma universalidade na queda livre (também conhecida como princípio da equivalência fraca, ou a igualdade universal da massa inercial e gravitacional passiva): a trajetória de um corpo de teste em queda livre depende apenas de sua posição e velocidade inicial, mas não de suas propriedades materiais.[19] Uma versão simplificada disso é incorporada na "experiência do elevador" de Einstein, ilustrada na figura à direita: para um observador numa pequena sala fechada, é impossível decidir, mapeando a trajetória de corpos como uma bola solta, se a sala está em repouso em um campo gravitacional ou em espaço livre a bordo de um foguete que está acelerando a um taxa igual à do campo gravitacional.[20]
Dada a universalidade da queda livre, não há distinção observável entre movimento inercial e movimento sob a influência da força gravitacional. Isso sugere a definição de uma nova classe de movimento inercial, a saber, a dos objetos em queda livre sob a influência da gravidade. Essa nova classe de movimentos preferidos também define uma geometria de espaço e tempo; em termos matemáticos, é o movimento geodésico associado a uma conexão específica que depende do gradiente do potencial gravitacional. O espaço, nessa construção, ainda possui a convencional geometria euclidiana. No entanto, o espaço-tempo como um todo é mais complicado. Como pode ser mostrado usando experimentos de pensamento simples seguindo as trajetórias de queda livre de diferentes partículas de teste, o resultado do transporte de vetores de espaço-tempo que podem denotar a velocidade de uma partícula variará com a trajetória da mesma; matematicamente falando, a conexão newtoniana não é integrável. A partir disso, pode-se deduzir que o espaço-tempo é curvo. A teoria de Newton-Cartan resultante é uma formulação geométrica da gravidade newtoniana usando apenas conceitos covariantes, ou seja, uma descrição que é válida em qualquer sistema de coordenadas desejado.[21] Nessa descrição geométrica, os efeitos de maré — a aceleração relativa de corpos em queda livre — estão relacionados à derivada da conexão, mostrando como a geometria modificada é causada pela presença de massa.[22]
Generalização relativista[editar | editar código-fonte]

Por mais intrigante que a gravidade geométrica newtoniana possa ser, sua base, a mecânica clássica, é meramente um caso limitante da mecânica relativista (especial).[23] Na linguagem da simetria: onde a gravidade pode ser desprezada, a física é uma invariante de Lorentz como na relatividade especial, e não uma invariante de Galileu como na mecânica clássica. (A definição de simetria da relatividade especial é o grupo de Poincaré, que inclui traduções, rotações e reforços.) As diferenças entre os dois tornam-se significativas quando se trata de velocidades que se aproximam da velocidade da luz e com fenômenos de alta energia.[24]
Com a simetria de Lorentz, estruturas adicionais entram em jogo. Elas são definidas pelo conjunto de cones em luz (ver imagem). Os cones de luz definem uma estrutura causal: para cada evento A, há um conjunto de eventos que podem, em princípio, influenciar ou ser influenciado por A por meio de sinais ou interações que não precisam viajar mais rápido que a luz (como o evento B na imagem) e um conjunto de eventos para os quais tal influência é impossível (como o evento C na imagem). Esses conjuntos são independentes do observador.[25] Em conjunto com a linha do espaço de partículas que caem livremente, os cones de luz podem ser usados para reconstruir a métrica semi-riemanniana do espaço-tempo, pelo menos até um fator escalar positivo. Em termos matemáticos, isso define uma estrutura conformada ou uma geometria conforme.[26]
Relatividade especial é definida na ausência de gravidade, portanto, para aplicações práticas, é um modelo adequado sempre que a gravidade pode ser desprezada. Colocando a gravidade em jogo, e assumindo a universalidade da queda livre, aplica-se um raciocínio análogo como na seção anterior: não há quadros inerciais globais. Em vez disso, existem quadros inerciais aproximados que se movem ao lado de partículas que caem livremente. Traduzido para a linguagem do espaço-tempo: as linhas retas que definem um referencial inercial livre de gravidade são deformadas para linhas curvas em relação umas às outras, sugerindo que a inclusão da gravidade requer uma mudança na geometria do espaço-tempo.[27]
A priori, não está claro se os novos quadros locais em queda livre coincidem com os referenciais nos quais as leis da relatividade especial são válidas — essa teoria é baseada na propagação da luz e, portanto, no eletromagnetismo, que poderia ter um conjunto diferente de quadros preferidos. Mas, usando diferentes suposições sobre os quadros especiais-relativísticos (como ser fixado na terra ou em queda livre), pode-se derivar previsões diferentes para o desvio para o vermelho gravitacional, isto é, a maneira pela qual a frequência de luz se desloca à medida que a luz se propaga através de um campo gravitacional. As medições reais mostram que os quadros de queda livre são aqueles em que a luz se propaga como na relatividade especial.[28] A generalização dessa afirmação, a saber, que as leis da relatividade restrita mantêm uma boa aproximação em referenciais de queda livre (e não rotativos), é conhecida como princípio da equivalência de Einstein, um princípio orientador crucial para generalizar a física relativista especial para incluir a gravidade.[29]
Os mesmos dados experimentais mostram que o tempo medido por relógios num campo gravitacional — tempo próprio, para dar o termo técnico — não segue as regras da relatividade especial. Na linguagem da geometria do espaço-tempo, ela não é medida pela métrica de Minkowski. Como no caso newtoniano, isso sugere uma geometria mais geral. Em escalas pequenas, todos os referenciais que estão em queda livre são equivalentes e aproximadamente minkowskianos. Consequentemente, estamos lidando agora com uma generalização curva do espaço de Minkowski. O tensor métrico que define a geometria — em particular, como os comprimentos e os ângulos são medidos — não é a métrica de Minkowski da relatividade especial, é uma generalização conhecida como métrica semi ou pseudoriemanniana. Além disso, cada métrica riemanniana é naturalmente associada a um tipo particular de conexão, a conexão de Levi-Civita, e esta é, de fato, a conexão que satisfaz o princípio da equivalência e torna o espaço localmente minkowskiano (isto é, em inerciais coordenadas localmente adequadas, a métrica é minkowskiana, e suas primeiras derivadas parciais e os coeficientes de conexão desaparecem).[30]
Equações de Einstein[editar | editar código-fonte]
Tendo formulado a versão relativista e geométrica dos efeitos da gravidade, a questão da fonte da gravidade permanece. Na gravidade newtoniana, a fonte é massa. Na relatividade especial, a massa acaba por ser parte de uma quantidade mais geral chamada de tensor de energia-momento, que inclui densidades de energia e de momento, bem como tensão: pressão e cisalhamento.[31] Usando o princípio da equivalência, este tensor é prontamente generalizado para o espaço-tempo curvo. Com base na analogia com a gravidade newtoniana geométrica, é natural supor que a equação de campo para a gravidade relaciona esse tensor com o tensor de Ricci, que descreve uma classe particular de efeitos de maré: a mudança de volume para uma pequena nuvem de partículas de teste que estão inicialmente em repouso e depois caem livremente. Na relatividade especial, a conservação de energia-momento corresponde à afirmação de que o tensor de energia-momento é livre de divergência. Essa fórmula também é prontamente generalizada para o espaço-tempo curvo, substituindo as derivadas parciais por suas contrapartes curvadas-múltiplas, derivadas covariantes estudadas na geometria diferencial. Com essa condição adicional — a divergência covariante do tensor energia-momento, e, portanto, de qualquer coisa que esteja do outro lado da equação, é zero — o conjunto mais simples de equações é chamado de equações (de campo) de Einstein:
Equações de campo de Einstein
Do lado esquerdo está o tensor de Einstein, uma combinação específica livre de divergência do tensor de Ricci e da métrica. Onde é simétrico. Em particular,
é a curvatura escalar. O próprio tensor de Ricci está relacionado com o tensor de curvatura de Riemann mais geral
Do lado direito, é o tensor energia-momento. Todos os tensores são escritos em notação de índices abstratos.[32] Combinando a previsão da teoria com resultados observacionais para órbitas planetárias ou, equivalentemente, assegurando que o limite de gravidade fraca e baixa velocidade é a mecânica newtoniana, a constante de proporcionalidade pode ser fixada como κ = 8πG/c4, com G a constante gravitacional e c a velocidade da luz.[33] Quando não há nenhuma matéria presente, de modo que o tensor de energia-momento desaparece, os resultados são as equações de vácuo de Einstein,
Alternativas à relatividade geral[editar | editar código-fonte]
Existem teorias alternativas à relatividade geral baseadas nas mesmas premissas, que incluem regras e/ou restrições adicionais, levando a diferentes equações de campo. Exemplos são a teoria de Whitehead, a teoria Brans-Dicke, o teleparalelismo, a gravidade de f(R) e a teoria de Einstein-Cartan.[34]
Definição e aplicações básicas[editar | editar código-fonte]
A derivação descrita na seção anterior contém todas as informações necessárias para definir a relatividade geral, descrever suas principais propriedades e abordar uma questão de importância crucial na física, ou seja, como a teoria pode ser usada para a construção de modelos.
Definição e propriedades básicas[editar | editar código-fonte]
A relatividade geral é uma teoria métrica da gravitação. Em seu cerne estão as equações de Einstein, que descrevem a relação entre a geometria de uma variedade pseudoriemanniana quadridimensional que representa o espaço-tempo e a energia-momento contida naquele espaço-tempo.[35] Fenômenos que na mecânica clássica são atribuídos à ação da força da gravidade (tais como queda livre, movimento orbital e trajetórias de espaçonaves), correspondem ao movimento inercial dentro de uma geometria curva do espaço-tempo na relatividade geral; não há força gravitacional desviando objetos de seus caminhos naturais e retos. Em vez disso, a gravidade corresponde a mudanças nas propriedades do espaço e do tempo, que por sua vez alteram os caminhos mais retos possíveis que os objetos seguirão naturalmente.[36] A curvatura é, por sua vez, causada pela energia-momento da matéria. Parafraseando o físico relativista norte-americano John Archibald Wheeler, o espaço-tempo diz à matéria como se mover; a matéria diz ao espaço-tempo como se curvar.[37]
Enquanto a relatividade geral substitui o potencial gravitacional escalar da física clássica por um tensor de grau-dois simétrico, o último reduz-se ao primeiro em certos casos limitantes. Para campos gravitacionais fracos e velocidade lenta em relação à velocidade da luz, as previsões da teoria convergem naquelas da lei de gravitação universal de Newton.[38]
Como é construída usando tensores, a relatividade geral exibe uma covariância geral: suas leis — e outras leis formuladas dentro do quadro geral relativista — assumem a mesma forma em todos os sistemas de coordenadas.[39] Além disso, a teoria não contém quaisquer estruturas de fundo geométricas invariantes, ou seja, é independência-fundo. Assim, satisfaz um princípio geral mais rigoroso da relatividade, ou seja, que as leis da física são as mesmas para todos os observadores.[40] Localmente, como expresso no princípio da equivalência, o espaço-tempo é minkowskiano, e as leis da física exibem a invariância local de Lorentz.[41]
Construção de modelos[editar | editar código-fonte]
O conceito central da construção de modelos gerais relativísticos é o de uma solução das equações de Einstein. Dadas as equações de Einstein e os cálculos adequados para as propriedades da matéria, tal solução consiste em uma variedade semi-riemanniana específica (geralmente definida dando-se a métrica em coordenadas específicas), e campos de matéria específica definidos nessa variedade. A matéria e a geometria devem satisfazer as equações de Einstein, portanto, em particular, o tensor de energia-momento da matéria deve ser livre de divergências. A matéria deve, é claro, também satisfazer as equações adicionais que foram impostas às suas propriedades. Em suma, tal solução é um modelo do universo que satisfaz as leis da relatividade geral e, possivelmente, leis adicionais que governam qualquer assunto que possa estar presente.[42]
As equações de Einstein são equações diferenciais parciais não-lineares e, como tal, difíceis de serem resolvidas com exatidão.[43] No entanto, várias soluções exatas são conhecidas, embora apenas algumas tenham aplicações físicas diretas.[44] As soluções exatas mais conhecidas, e também as mais interessantes do ponto de vista da física, são a solução de Schwarzschild, a solução de Reissner-Nordström e a métrica de Kerr, cada uma correspondendo a um certo tipo de buraco negro em um universo vazio,[45] e os universos Friedmann-Lemaître-Robertson-Walker e de Sitter, cada um descrevendo um cosmos em expansão.[46] Soluções exatas de grande interesse teórico incluem o universo de Gödel (que abre a intrigante possibilidade da viagem no tempo em espaços-tempos curvos), a solução de Taub–NUT (um modelo de universo que é homogêneo, mas anisotrópico) e o anti-espaço de Sitter (que recentemente ganhou destaque no contexto do que é chamado de conjectura Maldacena).[47]
Dada a dificuldade de encontrar soluções exatas, as equações de campo de Einstein também são resolvidas frequentemente por integração numérica num computador, ou considerando pequenas perturbações de soluções exatas. No campo da relatividade numérica, computadores poderosos são empregados para simular a geometria do espaço-tempo e resolver as equações de Einstein para situações interessantes, como dois buracos negros em colisão.[48] Em princípio, esses métodos podem ser aplicados a qualquer sistema, com recursos computacionais suficientes, e podem tratar de questões fundamentais, como singularidades nuas. Soluções aproximadas também podem ser encontradas por teorias de perturbação, como a gravidade linearizada[49] e sua generalização, a expansão pós-newtoniana, ambas desenvolvidas pelo cientista alemão. A última fornece uma abordagem sistemática para resolver a geometria de um espaço-tempo que contém uma distribuição de matéria que se move lentamente em comparação com a velocidade da luz. A expansão envolve uma série de termos; os primeiros termos representam a gravidade newtoniana, enquanto os termos posteriores representam correções cada vez menores à teoria de Newton, devido à relatividade geral.[50] Uma extensão dessa expansão é o formalismo parametrizado pós-newtoniano (PPN), que permite comparações quantitativas entre as previsões da relatividade geral e as teorias alternativas.[51]
Consequências da teoria de Einstein[editar | editar código-fonte]
A relatividade geral tem várias consequências físicas. Algumas seguem diretamente dos axiomas da teoria, enquanto outras se tornaram claras apenas no curso de muitos anos de pesquisa que se seguiram à publicação inicial de Einstein.
Dilatação do tempo gravitacional e mudança de frequência[editar | editar código-fonte]

Assumindo que o princípio da equivalência se mantenha,[52] a gravidade influencia a passagem do tempo. A luz enviada para o poço da gravidade é desviado para o azul, enquanto a luz enviada na direção oposta (ou seja, saindo do poço gravitacional) é desviada para o vermelho; coletivamente, esses dois efeitos são conhecidos como desvio de frequência gravitacional. De maneira mais geral, os processos próximos a um corpo massivo são mais lentos quando comparados aos processos que estão ocorrendo mais longe; este efeito é conhecido como dilatação do tempo gravitacional.[53]
O desvio para o vermelho gravitacional foi medido em laboratório[54] e usando observações astronômicas.[55] A dilatação do tempo gravitacional no campo gravitacional da Terra foi medida inúmeras vezes usando relógios atômicos,[56] enquanto a validação contínua é fornecida como um efeito colateral da operação do Sistema de Posicionamento Global (GPS).[57] Testes em campos gravitacionais mais fortes são fornecidos pela observação de pulsares binários.[58] Todos os resultados estão de acordo com a relatividade geral.[59] No entanto, no nível atual de precisão, essas observações não podem distinguir entre a relatividade geral e outras teorias em que o princípio de equivalência é válido.[60]
Deflexão de luz e atraso de tempo gravitacional[editar | editar código-fonte]
A relatividade geral prevê que o caminho da luz siga a curvatura do espaço-tempo ao passar perto de uma estrela. Este efeito foi inicialmente confirmado observando a luz das estrelas ou quasares distantes sendo desviados quando passa o Sol.[61]
Essa e outras previsões relacionadas derivam do fato de que a luz segue o que é chamado de geodésica nula ou leve — uma generalização das linhas retas ao longo das quais a luz viaja na física clássica. Tais geodésicas são a generalização da invariância da velocidade da luz na relatividade especial.[62] À medida que se examina os modelos de espaço-tempo adequados (seja a solução Schwarzschild externa ou, para mais de uma massa única, a expansão pós-newtoniana),[63] surgem vários efeitos da gravidade sobre a propagação da luz. Embora a curvatura da luz também possa ser derivada pela extensão da universalidade da queda livre à luz,[64] o ângulo de deflexão resultante de tais cálculos é apenas metade do valor dado pela relatividade geral.[65]
Intimamente relacionado à deflexão da luz está o atraso de tempo gravitacional (ou atraso de Shapiro), o fenômeno em que os sinais de luz demoram mais para se mover através de um campo gravitacional do que na ausência desse campo. Houve inúmeros testes bem-sucedidos dessa previsão.[66] No formalismo pós-newtoniano parametrizado (PPN), as medidas tanto da deflexão da luz quanto do atraso gravitacional determinam um parâmetro chamado γ, que codifica a influência da gravidade na geometria do espaço.[67]
Ondas gravitacionais[editar | editar código-fonte]

Previstas por Einstein em 1916,[68][69] as ondas gravitacionais são fenômenos que consistem em ondulações na métrica do espaço-tempo que se propagam na velocidade da luz. Estas são uma das várias analogias entre a gravidade do campo fraco e o eletromagnetismo, pois são análogas às ondas eletromagnéticas. Em 11 de fevereiro de 2016, a equipe do Observatório de Ondas Gravitacionais por Interferômetro Laser (LIGO) anunciou[70] que havia detectado diretamente ondas gravitacionais de um par de buracos negros se fundindo.[71][72][73]
O tipo mais simples de tal onda pode ser visualizada pela ação de um anel de partículas livremente flutuantes. Uma onda senoidal que se propaga através desse anel em direção ao leitor distorce o anel de uma maneira característica e rítmica (imagem animada à direita).[74] Como as equações de Einstein são não-lineares, ondas gravitacionais arbitrariamente fortes não obedecem à superposição linear, dificultando sua descrição. No entanto, para campos fracos, uma aproximação linear pode ser feita. Essas ondas gravitacionais linearizadas são suficientemente precisas para descrever as ondas extremamente fracas que espera-se que cheguem à Terra a partir de eventos cósmicos distantes, que tipicamente resultam em distâncias relativas aumentando e diminuindo em ou menos. Métodos de análise de dados usam rotineiramente o fato de que essas ondas linearizadas podem ser decompostas por Fourier.[75]
Algumas soluções exatas descrevem ondas gravitacionais sem qualquer aproximação, por exemplo, um trem de ondas que viaja através do espaço vazio[76] ou universos de Gowdy, variedades de um cosmos em expansão cheio de ondas gravitacionais.[77] Mas para ondas gravitacionais produzidas em situações astrofisicamente relevantes, como a fusão de dois buracos negros, os métodos numéricos são atualmente a única maneira de construir modelos apropriados.[78]
Efeitos orbitais e a relatividade da direção[editar | editar código-fonte]
Precessão de apsides[editar | editar código-fonte]

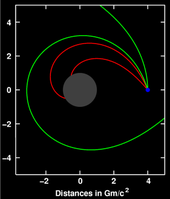
Na relatividade geral, os apsides (o ponto de aproximação mais extremo de um corpo em órbita no centro de massa do sistema) de qualquer órbita sofrerão precessão; a órbita não é uma elipse, mas semelhante a uma que gira em seu foco, resultando numa forma semelhante a uma curva rosa (ver imagem). Einstein derivou primeiro este resultado usando uma métrica aproximada representando o limite newtoniano e tratando o corpo em órbita como uma partícula de teste. Para ele, o fato de sua teoria ter dado uma explicação direta da mudança anômala do periélio de Mercúrio, descoberta anteriormente por Urbain Le Verrier em 1859, era uma evidência importante de que havia finalmente identificado a forma correta das equações do campo gravitacional.[79]
O efeito também pode ser derivado usando a métrica exata de Schwarzschild (descrevendo o espaço-tempo em torno de uma massa esférica)[80] ou o muito mais geral formalismo pós-newtoniano.[81] Isso ocorre devido à influência da gravidade na geometria do espaço e à contribuição da auto-energia para a gravidade do corpo (codificada na não-linearidade das equações de Einstein).[82] A precessão relativista foi observada em todos os planetas que permitem medições precisas de precessão (Mercúrio, Vênus e Terra),[83] bem como em sistemas de pulsares binários, onde é superior a cinco ordens de grandeza.[84]
Na relatividade geral, o deslocamento do periélio σ, expresso em radianos por revolução, é dado aproximadamente por:[85]
onde
- é o semieixo maior
- é o período orbital
- é a velocidade da luz
- é a excentricidade orbital
Decaimento orbital[editar | editar código-fonte]

De acordo com a relatividade geral, um sistema binário emitirá ondas gravitacionais, perdendo energia. Devido a essa perda, a distância entre os dois corpos em órbita diminui, assim como o seu período orbital. Dentro do Sistema Solar ou de estrelas duplas comuns, o efeito é muito pequeno para ser observável. Este não é o caso de um pulsar binário próximo, um sistema de duas estrelas de nêutrons em órbita, uma das quais é um pulsar: a partir do pulsar, os observadores na Terra recebem uma série regular de pulsos de rádio que podem servir como um relógio altamente preciso, que permite medições precisas do período orbital.[87]
A primeira observação de uma diminuição no período orbital devido à emissão de ondas gravitacionais foi feita por Hulse e Taylor, usando o pulsar binário PSR 1913+16 que haviam descoberto em 1974. Esta foi a primeira detecção de ondas gravitacionais, embora indiretas, pelas quais foram agraciados com o Prêmio Nobel de Física em 1993.[88] Desde então, vários outros pulsares binários foram encontrados, em particular o pulsar duplo PSR J0737-3039, no qual ambas as estrelas são pulsares.[89]
Precessão geodésica e arraste de referenciais[editar | editar código-fonte]
Vários efeitos relativísticos estão diretamente relacionados à relatividade da direção.[90] Uma é a precessão geodésica: a direção do eixo de um giroscópio em queda livre no espaço-tempo curvo mudará quando comparada, por exemplo, com a direção da luz recebida de estrelas distantes – mesmo que tal giroscópio represente a maneira de manter uma direção o mais estável possível ("transporte paralelo").[91] Para o sistema Lua-Terra, esse efeito foi medido com a ajuda do laser lunar.[92] Mais recentemente, foi medido para massas de teste a bordo do satélite Gravity Probe B com uma precisão melhor que 0,3%.[93][94]
Perto de uma massa rotativa, existem efeitos gravitomagnéticos ou de arrastamento da estrutura. Um observador distante determinará que objetos próximos à massa serão "arrastados". Isso é mais extremo para buracos negros rotativos onde, para qualquer objeto que entre numa zona conhecida como ergosfera, a rotação é inevitável.[95] Tais efeitos podem ser novamente testados através de sua influência na orientação dos giroscópios em queda livre.[96] Testes um pouco controversos foram realizados usando os satélites LAGEOS, confirmando a previsão relativista.[97] Também foi usada a sonda Mars Global Surveyor em torno de Marte.[98][99]
Aplicações astrofísicas[editar | editar código-fonte]
Lente gravitacional[editar | editar código-fonte]

A deflexão da luz pela gravidade é responsável por uma nova classe de fenômenos astronômicos. Se um objeto massivo estiver situado entre o astrônomo e um objeto alvo distante, com massa apropriada e distâncias relativas, o astrônomo verá múltiplas imagens distorcidas do alvo. Tais efeitos são conhecidos como lentes gravitacionais.[100] Dependendo da configuração, escala e distribuição de massa, pode haver duas ou mais imagens, um anel brilhante conhecido como anel de Einstein ou anéis parciais chamados de arcos.[101] O primeiro exemplo foi descoberto em 1979;[102] desde então, mais de cem lentes gravitacionais foram observadas.[103] Mesmo se as múltiplas imagens estiverem muito próximas umas das outras para serem resolvidas, o efeito ainda pode ser medido, por exemplo, como um brilho geral do objeto alvo; vários desses "eventos de microlente" foram observados.[104]
As lentes gravitacionais transformaram-se numa ferramenta da astronomia observacional. São usadas para detectar a presença e distribuição de matéria escura, fornecer um "telescópio natural" para observar galáxias distantes e obter uma estimativa independente da constante de Hubble. Avaliações estatísticas de dados de lentes apresentam informações valiosas sobre a evolução estrutural das galáxias.[105]
Astronomia de onda gravitacional[editar | editar código-fonte]

Observações de pulsares binários fornecem fortes evidências indiretas para a existência de ondas gravitacionais. A detecção dessas ondas foi por anos um dos principais objetivos de recentes pesquisas relacionadas à relatividade.[106] Vários detectores de ondas gravitacionais terrestres estão atualmente em operação, principalmente os detectores interferométricos GEO600, LIGO (dois detectores), TAMA 300 e VIRGO.[107] Várias matrizes de temporização de pulsares estão usando pulsares de milissegundos para detectar ondas gravitacionais na faixa de freqüência de 10−9 a 10−6 Hertz que originam-se de buracos negros supermassivos binários.[108] Um detector baseado no espaço europeu, eLISA / NGO, está atualmente em desenvolvimento,[109] com uma missão precursora (LISA Pathfinder) lançada em dezembro de 2015.[110]
Observações de ondas gravitacionais prometem complementar observações no espectro eletromagnético.[111] Espera-se que eles forneçam informações sobre buracos negros e outros objetos densos, como estrelas de nêutrons e anãs brancas, sobre certos tipos de implosões de supernovas, e sobre processos no universo primitivo, incluindo a assinatura de certos tipos de sequências cósmicas hipotéticas.[112] Em fevereiro de 2016, a equipe Advanced LIGO anunciou que havia detectado ondas gravitacionais de uma fusão de buraco negro.[71][72][73]
Buracos negros e outros objetos compactos[editar | editar código-fonte]
Sempre que a relação entre a massa de um objeto e seu raio se torna suficientemente grande, a relatividade geral prediz a formação de um buraco negro, uma região do espaço da qual nada, nem mesmo a luz, pode escapar. Nos modelos atualmente aceitos de evolução estelar, estrelas de nêutrons com cerca de 1,4 massa solar e buracos negros estelares com algumas dezenas de massas solares são considerados o estado final para a evolução de estrelas massivas.[113] Normalmente, uma galáxia tem um buraco negro supermassivo com alguns milhões até alguns bilhões de massas solares em seu centro,[114] e acredita-se que sua presença tenha desempenhado um papel importante na formação da galáxia e de estruturas cósmicas maiores.[115]

Astronomicamente, a propriedade mais importante dos objetos compactos é que eles fornecem um mecanismo extremamente eficiente para converter a energia gravitacional em radiação eletromagnética.[116] Acredita-se que a acreção, a queda de poeira ou matéria gasosa em buracos negros estelares ou supermassivos, seja responsável por alguns objetos astronômicos espetacularmente luminosos, notavelmente diversos tipos de núcleos galácticos ativos em escalas galácticas e objetos de tamanho estelar, como microquasares.[117] Em particular, a acreção pode levar a jatos relativísticos, feixes concentrados de partículas altamente energéticas que são lançadas no espaço a uma velocidade quase que à luz.[118] A relatividade geral desempenha um papel central na modelagem de todos esses fenômenos,[119] e as observações fornecem fortes evidências para a existência de buracos negros com as propriedades previstas pela teoria.[120]
Buracos negros também são fenômenos procurados na busca por ondas gravitacionais (ver seção Ondas gravitacionais, acima). Mesclar buracos negros binários deve levar a alguns dos mais fortes sinais de ondas gravitacionais a atingir detectores na Terra, e a fase diretamente antes da fusão ("chilro") pode ser usada como uma "vela padrão" para deduzir a distância até os eventos de fusão – e, portanto, servem como uma sonda de expansão cósmica a grandes distâncias.[121] As ondas gravitacionais produzidas como um buraco negro estelar em um supermassivo devem fornecer informações diretas sobre a geometria do buraco negro supermassivo.[122]
Cosmologia[editar | editar código-fonte]

Os modelos atuais de cosmologia são baseados nas equações de campo de Einstein, que incluem a constante cosmológica , visto que esta exerce importante influência na dinâmica de larga escala do cosmos:
onde é a métrica do espaço-tempo.[123] As soluções isotrópicas e homogêneas dessas equações aprimoradas, as soluções de Friedmann-Lemaître-Robertson-Walker,[124] permitem que os físicos modelem um universo que evoluiu nos últimos 14 bilhões de anos a partir de uma fase inicial quente do Big Bang.[125] Uma vez que um pequeno número de parâmetros (por exemplo, a densidade de matéria média do universo) foi fixado por observação astronômica,[126] outros dados observacionais podem ser usados para testar os modelos.[127] As previsões, todas bem-sucedidas, incluem a abundância inicial de elementos químicos formados em um período de nucleossíntese primordial,[128] a estrutura em larga escala do universo[129] e a existência e propriedades de um "eco térmico" do início do cosmos, a radiação cósmica de fundo.[130]
As observações astronômicas da taxa de expansão cosmológica permitem estimar a quantidade total de matéria no universo, embora a natureza dessa matéria em parte permaneça misteriosa. Cerca de 90% de toda a matéria parece ser matéria escura, que possui massa (ou, equivalentemente, influência gravitacional), mas não interage eletromagneticamente e, portanto, não pode ser observada diretamente.[131] Não existe uma descrição geralmente aceita desse novo tipo de matéria, dentro da estrutura da física de partículas[132] conhecida ou não.[133] Evidências observacionais de pesquisas no desvio para o vermelho de supernovas distantes e medidas da radiação cósmica de fundo também mostram que a evolução do nosso universo é significativamente influenciada por uma constante cosmológica que resulta em uma aceleração da expansão cósmica ou, equivalente, por uma forma de energia com uma equação incomum de estado, conhecido como energia escura, cuja natureza permanece incerta.[134]
Uma fase inflacionária,[135] uma etapa adicional de expansão fortemente acelerada em tempos cósmicos de cerca de 10−33 segundos, foi levantada como hipótese em 1980 para explicar várias observações intrigantes que não eram explicadas pelos modelos cosmológicos clássicos, como a homogeneidade quase perfeita da radiação cósmica de fundo.[136] Medições recentes da radiação cósmica de fundo resultaram na primeira evidência desse cenário.[137] No entanto, existe uma variedade desconcertante de possíveis cenários inflacionários, que não podem ser restringidos pelas observações atuais.[138] Uma questão ainda maior é a física do universo primitivo, anterior à fase inflacionária e próxima de onde os modelos clássicos preveem a singularidade do Big Bang. Uma resposta autoritária exigiria uma teoria completa da gravidade quântica, que ainda não foi desenvolvida.[139]
Viagem no tempo[editar | editar código-fonte]
Kurt Gödel mostrou que existem soluções para as equações de Einstein que contêm curvas fechadas de tempo, que permitem loops no tempo. As soluções exigem condições físicas extremas que dificilmente ocorrerão na prática, e permanece uma questão em aberto se outras leis da física as eliminarão completamente. Desde então, foram encontradas outras soluções da relatividade geral – igualmente impraticáveis – contendo curvas fechadas de tempo, como o cilindro de Tipler e buracos de minhoca atravessáveis.[140]
Conceitos avançados[editar | editar código-fonte]
Estrutura causal e geometria global[editar | editar código-fonte]

Na relatividade geral, nenhum corpo material pode alcançar ou ultrapassar um pulso de luz. Nenhuma influência de um evento A pode chegar a qualquer outro local X antes que a luz seja enviada de A a X. Em consequência, uma exploração de todas as linhas mundiais leves (geodésica nula) produz informações importantes sobre a estrutura causal do espaço-tempo. Essa estrutura pode ser exibida usando diagramas de Penrose-Carter, em que regiões infinitamente grandes de espaço e intervalos de tempo infinitos são reduzidos ("compactados") para caber em um mapa finito, enquanto a luz ainda viaja ao longo das diagonais, como nos diagramas de espaço-tempo padrão.[141]
Consciente da importância da estrutura causal, Roger Penrose e outros desenvolveram o que é conhecido como geometria global. Na geometria global, o objeto de estudo não é uma solução específica (ou família de soluções) para as equações de Einstein. Em vez disso, relações que são verdadeiras para todos os geodésicos, como a equação de Raychaudhuri, e suposições adicionais não específicas sobre a natureza da matéria (geralmente na forma de condições de energia) são usadas para derivar resultados gerais.[142]
Horizontes[editar | editar código-fonte]
Usando a geometria global, pode-se mostrar que algumas vezes o espaço-tempo contêm limites chamados horizontes, que delimitam uma região do restante do espaço-tempo. Os exemplos mais conhecidos são buracos negros: se a massa é comprimida em uma região suficientemente compacta do espaço (conforme especificado na conjectura do aro, a escala de comprimento relevante é o raio de Schwarzschild),[143] nenhuma luz do interior pode escapar para o exterior. Como nenhum objeto pode ultrapassar um pulso de luz, toda a matéria interior também é aprisionada. A passagem do exterior para o interior ainda é possível, mostrando que a fronteira, o horizonte do buraco negro, não é uma barreira física.[144]

Os primeiros estudos sobre buracos negros baseavam-se em soluções explícitas das equações de Einstein, principalmente na solução esférica simétrica de Schwarzschild (usada para descrever um buraco negro estático) e na axissimétrica solução de Kerr (usada para descrever um buraco negro rotativo e estacionário e introduzir recursos interessantes, como a ergosfera). Usando a geometria global, estudos posteriores revelaram propriedades mais gerais dos buracos negros. Com o tempo, eles se tornam objetos bastante simples, caracterizados por onze parâmetros, especificando: carga elétrica, energia de massa, momento linear, momento angular e localização em um horário especificado. Isto é afirmado pelo teorema da singularidade do buraco negro: "buracos negros não têm cabelo", isto é, sem marcas distintivas como os penteados dos humanos. Independentemente da complexidade de um objeto gravitacional em colapso para formar um buraco negro, o objeto resultante (tendo emitido ondas gravitacionais) é muito simples.[145]
Ainda mais notavelmente, existe um conjunto geral de leis conhecidas como mecânica dos buracos negros, que é análoga às leis da termodinâmica. Por exemplo, pela segunda lei da mecânica dos buracos negros, a área do horizonte de eventos de um buraco negro geral nunca diminuirá com o tempo, análoga à entropia de um sistema termodinâmico. Isso limita a energia que pode ser extraída por meios clássicos de um buraco negro em rotação (por exemplo, pelo processo Penrose).[146] Há fortes evidências de que as leis da mecânica dos buracos negros são, de fato, um subconjunto das leis da termodinâmica e que a área do buraco negro é proporcional à sua entropia.[147] Isso leva a uma modificação das leis originais da mecânica dos buracos negros: por exemplo, quando a segunda lei da mecânica dos buracos negros se torna parte da segunda lei da termodinâmica, é possível que a área dos buracos negros diminua – desde que outros processos garantam que, em geral, a entropia aumente. Como objetos termodinâmicos com temperatura diferente de zero, os buracos negros devem emitir radiação térmica. Cálculos semi-clássicos indicam que sim, com a gravidade da superfície desempenhando o papel da temperatura na lei de Planck. Essa radiação é conhecida como radiação Hawking.[148]
Existem outros tipos de horizontes. Em um universo em expansão, um observador pode achar que algumas regiões do passado não podem ser observadas ("horizonte de partículas"), e algumas regiões do futuro não podem ser influenciadas (horizonte de eventos).[149] Mesmo no espaço plano de Minkowski, quando descrito por um observador acelerado (espaço de Rindler), haverá horizontes associados a uma radiação semi-clássica conhecida como radiação de Unruh.[150]
Singularidades[editar | editar código-fonte]
Outra característica universal da relatividade geral é o aparecimento de limites do espaço-tempo conhecidos como singularidades. O espaço-tempo pode ser explorado acompanhando geodésicas semelhantes ao tempo e à luz – todas maneiras possíveis pelas quais a luz e as partículas em queda livre podem viajar. Mas algumas soluções das equações de Einstein têm "bordas irregulares" – regiões conhecidas como singularidade espaço-tempo, onde os caminhos da luz e das partículas que caem chegam a um fim abrupto, e a geometria fica mal definida. Nos casos mais interessantes, são as "singularidades da curvatura", onde as quantidades geométricas que caracterizam a curvatura do espaço-tempo, como a escalar de Ricci, assumem valores infinitos.[151] Exemplos bem conhecidos de espaços-tempos com singularidades futuras – onde as linhas do mundo terminam – são a solução de Schwarzschild, que descreve uma singularidade dentro de um buraco negro estático eterno,[152] ou a solução de Kerr com sua singularidade em forma de anel dentro de um buraco negro rotativo eterno.[153] As soluções de Friedmann–Lemaître–Robertson–Walker e outros espaços-tempos que descrevem universos têm singularidades passadas nas quais as linhas do mundo começam, ou seja, singularidades do Big Bang, e algumas também possuem singularidades futuras (Big Crunch).[154]
Dado que todos esses exemplos são altamente simétricos – e, portanto, simplificados –, é tentador concluir que a ocorrência de singularidades é um objeto de idealização.[155] Os famosos teoremas da singularidade, provados usando os métodos da geometria global, dizem o contrário: as singularidades são uma característica genérica da relatividade geral e inevitáveis, visto que o colapso de um objeto com propriedades de matéria realistas transcende um certo estágio[156] e também no início de uma ampla classe de universos em expansão.[157] No entanto, os teoremas dizem pouco sobre as propriedades das singularidades, e grande parte da pesquisa atual é dedicada à caracterização da estrutura genérica dessas entidades (hipotetizada, por exemplo, pela conjectura BKL).[158] A hipótese da censura cósmica afirma que todas as singularidades futuras realistas (sem simetrias perfeitas, matéria com propriedades realistas) são escondidas com segurança atrás de um horizonte e, portanto, invisíveis a todos os observadores distantes. Embora ainda não exista uma prova formal, as simulações numéricas oferecem evidências de sua validade.[159]
Equações de evolução[editar | editar código-fonte]
Cada solução da equação de Einstein abrange toda a história de um universo – não é apenas um instantâneo de como as coisas são, mas um espaço-tempo inteiro, possivelmente cheio de matéria. Descreve o estado da matéria e da geometria em todos os lugares e a todo momento naquele universo em particular. Devido à sua covariância geral, a teoria de Einstein não é suficiente por si só para determinar a evolução temporal do tensor métrico. Ele deve ser combinado com uma condição de coordenada, que é análoga à fixação de gauge em outras teorias de campo.[160]
Para entender as equações de Einstein como equações diferenciais parciais, é útil formulá-las de uma maneira que descreva a evolução do universo ao longo do tempo. Isso é feito em formulações "3+1", onde o espaço-tempo é dividido em três dimensões espaciais e uma dimensão temporal. O exemplo mais conhecido é o formalismo ADM.[161] Essas decomposições mostram que as equações de evolução do espaço-tempo da relatividade geral são bem-comportadas: as soluções sempre existem e são definidas de maneira única, uma vez que condições iniciais adequadas foram especificadas.[162] Tais formulações das equações de campo de Einstein são a base da relatividade numérica.[163]
Quantidades globais e quase locais[editar | editar código-fonte]
A noção de equações da evolução está intimamente ligada a outro aspecto da física relativística geral. Na teoria de Einstein, é impossível encontrar uma definição geral para uma propriedade aparentemente simples, como a massa total (ou energia) de um sistema. A principal razão é que o campo gravitacional – como qualquer campo físico – deve receber uma determinada energia, mas que é fundamentalmente impossível essa energia ser localizada.[164]
No entanto, existem possibilidades para definir a massa total de um sistema, usando um hipotético "observador infinitamente distante" (massa ADM)[165] ou simetrias adequadas (massa de Komar).[166] Se alguém excluir da massa total do sistema a energia que é transportada para o infinito por ondas gravitacionais, o resultado é a massa de Bondi no infinito nulo.[167] Assim como na física clássica, pode-se demonstrar que essas massas são positivas.[168] Existem definições globais correspondentes para momento e momento angular.[169] Também houve várias tentativas para definir quantidades quase locais, como a massa de um sistema isolado formulado usando apenas quantidades definidas dentro de uma região finita de espaço que contém esse sistema. A esperança é obter uma quantidade útil para confirmações gerais sobre sistemas isolados, como uma formulação mais precisa da conjectura do aro.[170]
Relação com a teoria quântica[editar | editar código-fonte]
Se a relatividade geral fosse considerada um dos dois pilares da física moderna, a teoria quântica, a base da compreensão da matéria das partículas elementares à física do estado sólido, seria a outra.[171] No entanto, como reconciliar a teoria quântica com a relatividade geral ainda é uma questão em aberto.
Teoria quântica de campos no espaço-tempo curvo[editar | editar código-fonte]
As teorias quânticos de campos comuns, que formam a base da física moderna de partículas elementares, são definidas no espaço plano de Minkowski, que é uma excelente aproximação quando se trata de descrever o comportamento de partículas microscópicas em campos gravitacionais fracos, como os encontrados na Terra.[172] Para descrever situações nas quais a gravidade é forte o suficiente para influenciar a matéria (quântica), mas não forte o suficiente para exigir a própria quantização, os físicos formularam teorias quânticas de campos no espaço-tempo curvo. Essas teorias baseiam-se na relatividade geral para descrever um espaço-tempo de fundo curvo e definem uma teoria generalizada de campos quânticos para descrever o comportamento da matéria quântica dentro desse espaço-tempo.[173] Usando esse formalismo, pode ser demonstrado que os buracos negros emitem um espectro de corpos negros conhecido como radiação Hawking, levando à possibilidade de que eles evaporem com o tempo.[174] Como mencionado brevemente acima, essa radiação desempenha um papel importante na termodinâmica dos buracos negros.[175]
Gravidade quântica[editar | editar código-fonte]
A demanda por consistência entre uma descrição quântica da matéria e uma descrição geométrica do espaço-tempo,[176] bem como o aparecimento de singularidades (onde as escalas de comprimento das curvaturas tornam-se microscópicas), indicam a necessidade de uma teoria completa da gravidade quântica: para uma descrição adequada do interior dos buracos negros e do universo primitivo, é necessária uma teoria na qual a gravidade e a geometria associada do espaço-tempo sejam descritas na linguagem da física quântica.[177] Apesar dos grandes esforços, nenhuma teoria completa e consistente da gravidade quântica é atualmente conhecida, embora existam várias candidatas promissores.[178][179]

Tentativas de generalizar teorias comuns de campos quânticos, usadas na física de partículas elementares para descrever interações fundamentais, de modo a incluir a gravidade, levaram a sérios problemas.[180] Alguns argumentaram que, com baixas energias, essa abordagem é bem-sucedida, na medida em que resulta em uma efetiva teoria da gravidade (quântica) aceitável.[181] Em energias muito altas, no entanto, os resultados perturbadores são muito divergentes e levam a modelos desprovidos de poder preditivo ("não-renormalizabilidade perturbativa").[182]

Uma tentativa de superar essas limitações é a teoria das cordas, uma teoria quântica não de partículas pontuais, mas de pequenos objetos estendidos unidimensionais.[183] A teoria promete ser uma descrição unificada de todas as partículas e interações, incluindo a gravidade;[184] o preço a pagar são características incomuns, como seis dimensões extras de espaço, além das três usuais.[185] Na chamada segunda revolução das supercordas, conjeturou-se que tanto a teoria das cordas quanto a unificação da relatividade geral e da supersimetria conhecidas como supergravidade[186] fazem parte de um modelo hipotético onze-dimensional conhecido como teoria-M, que constituiria uma teoria consistente e exclusivamente definida da gravidade quântica.[187]
Outra abordagem começa com os procedimentos de quantização canônica da teoria quântica. Usando a formulação de valor inicial da relatividade geral (cf. equações de evolução acima), o resultado é a equação de Wheeler–DeWitt (um análogo da equação de Schrödinger) que, lamentavelmente, acaba sendo mal definida sem um corte (de rede) ultravioleta adequado.[188] No entanto, com a introdução do que agora são conhecidas como variáveis de Ashtekar,[189] isso leva a um modelo promissor conhecido como gravidade quântica em loop. O espaço é representado por uma estrutura semelhante à web chamada rede de spin, evoluindo ao longo do tempo em etapas discretas.[190]
Dependendo de quais características da relatividade geral e da teoria quântica são aceitas inalteradas, e em que mudanças de nível são introduzidas,[191] existem inúmeras outras tentativas para chegar a uma teoria viável da gravidade quântica, alguns exemplos são a teoria da gravidade em treliça baseada na Formulação Integral de Caminho de Feynman e no Cálculo de Regge,[178] triangulações dinâmicas,[192] conjuntos causais,[193] modelos de torção[194] ou modelos baseados na integral de caminho da cosmologia quântica.[195]
Todas as teorias candidatas ainda têm grandes problemas formais e conceituais a serem superados. Também enfrentam o problema comum de que, até o momento, não há como colocar previsões de gravidade quântica em testes experimentais (e, assim, decidir entre as candidatas onde suas previsões variam), embora exista esperança de que isso mude à medida que dados futuros de observações cosmológicas e experimentos de física de partículas estiverem disponíveis.[196]
Situação atual[editar | editar código-fonte]

A relatividade geral tem emergido como um modelo altamente bem-sucedido de gravitação e cosmologia, que até agora tem subsistido a cada prova inequívoca de observação e experimentação. Mesmo assim, há fortes indícios de que a teoria seja incompleta.[197] O problema da gravitação quântica e a questão da realidade da singularidade gravitacional permanecem abertos. Dados de observação que são tomados como prova de energia escura e matéria escura poderiam indicar a necessidade de uma nova física e, enquanto a chamada Anomalia das Pioneers ainda poderia admitir uma explicação convencional, ela também poderia ser um prenúncio de uma nova física.[198] Mesmo considerando essas questões, a relatividade geral é rica em possibilidades de exploração adicional. Matemáticos relativistas procuram entender a natureza das singularidades e das propriedades fundamentais das equações de Einstein,[199] e simulações de computador cada vez mais poderosas (como aquelas que descrevem fusão de buracos negros) são executadas.[200][201][202] Um século após a sua publicação, a relatividade geral continua a ser uma área muito ativa de investigação.[203]
Diversos experimentos têm confirmado as previsões teóricas da relatividade geral (ver seção Aplicações astrofísicas, acima). Em dezembro de 2018 foi anunciado mais um resultado: dois grupos que trabalharam de forma independente mediram o efeito do campo gravitacional em relógios atômicos. Os pesquisadores mediram ao longo de três anos a frequência de masers de hidrogênio a bordo de dois satélites do projeto Galileo lançados em 2014 que descrevem órbitas elípticas em torno da Terra. Ao determinarem como a frequência varia em função da altitude, foram capazes de obter um resultado que é 5,6 vezes melhor do que as medidas até então disponíveis.[204]
Ver também[editar | editar código-fonte]
- Ação de Einstein–Hilbert
- Deflexão da luz
- Cálculo de Ricci
- Controvérsia sobre a paternidade da teoria da relatividade
- Geometria e Experiência
- Propulsão Alcubierre
- Teoria das singularidades
Notas[editar | editar código-fonte]
- Este artigo foi inicialmente traduzido, total ou parcialmente, do artigo da Wikipédia em inglês cujo título é «General relativity».
Referências
- ↑ «GW150914: LIGO Detects Gravitational Waves». black-holes.org (em inglês). Consultado em 29 de setembro de 2017
- ↑ Landau & Lifshitz 1975, p. 228.
- ↑ O'Connor, J.J.; Robertson, E.F. (1996). «General relativity». Escola de Matemática e Estatística da Universidade de St. Andrews. Mathematical Physics Index. Consultado em 30 de setembro de 2017
- ↑ Pais 1982, capítulo 9 ao 15, Janssen 2005; um acervo atualizado de pesquisas recentes, incluindo reimpressões de muitos dos artigos originais, está em Renn 2007; uma visão geral acessível pode ser encontrada em Renn 2005, pp. 110ff. Os documentos originais de Einstein são encontrados em Digital Einstein, volumes 4 e 6. Um artigo chave inicial é Einstein 1907, cf. Pais 1982, capítulo 9. A publicação com as equações de campo está em Einstein 1915, ch. Pais 1982, capítulos 11–15
- ↑ Schwarzschild 1916a, Schwarzschild 1916b e Reissner 1916 (mais tarde complementado em Nordström 1918)
- ↑ Einstein 1917, cf. Pais 1982, ch. 15e
- ↑ O artigo original de Hubble é Hubble 1929; uma visão geral acessível é apresentada por Singh 2004, capítulos 2–4
- ↑ Conforme relatado por Gamow 1970. A condenação de Einstein seria prematura, confronte pode ser visto na seção Cosmologia
- ↑ Pais 1982, pp. 253–254
- ↑ Kennefick 2005, Kennefick 2007
- ↑ Pais 1982, ch. 16
- ↑ Thorne 2003, p. 74.
- ↑ Israel 1987, ch. 7.8–7.10, Thorne 1994, ch. 3–9
- ↑ Veja as seções "Efeitos orbitais e a relatividade da direção", "Dilatação do tempo gravitacional e mudança de frequência" e "Deflexão de luz e atraso de tempo gravitacional", e suas referências.
- ↑ Seção Cosmologia e referências nela contidas; o desenvolvimento histórico está em Overbye 1999
- ↑ A exposição a seguir re-traça a de Ehlers 1973, seção 1
- ↑ Arnold 1989, ch. 1
- ↑ Ehlers 1973, pp. 5f
- ↑ Will 1993, seção 2.4, Will 2006, seção 2
- ↑ Wheeler 1990, ch. 2
- ↑ Ehlers 1973, seção 1.2, Havas 1964, Künzle 1972. O simples experimento mental em questão foi descrito pela primeira vez em Heckmann & Schücking 1959
- ↑ Ehlers 1973, pp. 10f
- ↑ Boas introduções são, em ordem crescente de conhecimento pressuposto em matemática, Giulini 2005, Mermin 2005 e Rindler 1991; para relatos de experimentos de precisão, cf. parte IV de Ehlers & Lämmerzahl 2006
- ↑ Uma comparação aprofundada entre os dois grupos de simetria pode ser encontrada em Giulini 2006a
- ↑ Rindler 1991, seção 22, Synge 1972, seção 1 e 2
- ↑ Ehlers 1973, seção 2.3
- ↑ Ehlers 1973, seção 1.4, Schutz 1985, seção 5.1
- ↑ Ehlers 1973, pp. 17ff; uma derivação pode ser encontrada em Mermin 2005, ch. 12. Para a evidência experimental, cf. a secção Dilatação do tempo gravitacional e mudança de frequência, abaixo.
- ↑ Rindler 2001, seção 1.13; para um relato elementar, veja Wheeler 1990, ch. 2; existem, no entanto, algumas diferenças entre a versão moderna e o conceito original de Einstein usado na derivação histórica da relatividade geral, cf. Norton 1985
- ↑ Ehlers 1973, seção 1.4 para a evidência experimental, veja mais uma vez a seção "Dilatação do tempo gravitacional e mudança de frequência". Escolher uma conexão diferente com uma torção diferente de zero leva a uma teoria modificada conhecida como teoria de Einstein–Cartan.
- ↑ Ehlers 1973, p. 16, Kenyon 1990, seção 7.2, Weinberg 1972, seção 2.8
- ↑ Ehlers 1973, pp. 19–22; para derivações similares, ver seções 1 e 2 do cap. 7 em Weinberg 1972. O tensor de Einstein é o único tensor livre de divergência que é uma função dos coeficientes métricos, sua primeira e segunda derivadas no máximo, e permite que o espaço-tempo da relatividade especial seja uma solução na ausência de fontes de gravidade, confira Lovelock 1972. Os tensores de ambos os lados são de segunda ordem, ou seja, eles podem ser considerados como matrizes 4×4, cada um contendo dez termos independentes; assim, o acima representa dez equações acopladas. O fato de que, como consequência de relações geométricas conhecidas como identidades de Bianchi, o tensor de Einstein satisfaz mais quatro identidades reduzindo estas a seis equações independentes, p. ex. Schutz 1985, seção 8.3
- ↑ Kenyon 1990, seção 7.4
- ↑ Brans & Dicke 1961, Weinberg 1972, seção 3 no cap. 7, Goenner 2004, seção 7.2, e Trautman 2006, respectivamente
- ↑ Wald 1984, capítulo 4, Weinberg 1972, capítulo 7 ou, de fato, qualquer outro livro sobre relatividade geral
- ↑ Pelo menos aproximadamente, cf. Poisson 2004
- ↑ Wheeler 1990, p. xi
- ↑ Wald 1984, sec. 4.4
- ↑ Wald 1984, sec. 4.1
- ↑ Para as dificuldades (conceituais e históricas) de definir um princípio geral de relatividade e separá-lo da noção de covariância geral, veja Giulini 2007
- ↑ Seção 5 do capítulo 12 de Weinberg 1972
- ↑ Capítulos introdutórios de Stephani et al. 2003
- ↑ Uma revisão mostrando a equação de Einstein no contexto mais amplo de outras equações diferenciais parciais com significado físico é Geroch 1996
- ↑ Para informações básicas e uma lista de soluções, cf. Stephani et al. 2003; uma revisão mais recente pode ser encontrada em MacCallum 2006
- ↑ Chandrasekhar 1983, ch. 3,5,6
- ↑ Narlikar 1993, ch. 4, sec. 3.3
- ↑ Breves descrições destas e outras soluções interessantes podem ser encontradas em Hawking & Ellis 1973, capítulo 5
- ↑ Lehner 2002
- ↑ Por exemplo Wald 1984, sec. 4.4
- ↑ Will 1993, seção 4.1 e 4.2
- ↑ Will 2006, sec. 3.2, Will 1993, ch. 4
- ↑ Rindler 2001, pp. 24–26 vs. pp. 236–237 e Ohanian & Ruffini 1994, pp. 164–172. Einstein derivou esses efeitos usando o princípio da equivalência já em 1907, cf. Einstein 1907 e a descrição em Pais 1982, pp. 196–198
- ↑ Rindler 2001, pp. 24–26; Misner, Thorne & Wheeler 1973, § 38.5
- ↑ Experimento de Pound-Rebka, veja Pound & Rebka 1959, Pound & Rebka 1960; Pound & Snider 1964; uma lista de novas experiências é dada em Ohanian & Ruffini 1994, tabela 4.1 na p. 186
- ↑ Greenstein, Oke & Shipman 1971; as mais recentes e mais precisas medições Sirius B são publicadas em Barstow, Bond et al. 2005.
- ↑ Começando com o experimento Hafele–Keating, Hafele & Keating 1972a e Hafele & Keating 1972b, e culminando na experiência da Sonda Gravitacional A; uma visão geral dos experimentos pode ser encontrada em Ohanian & Ruffini 1994, tabela 4.1 na p. 186
- ↑ O GPS é continuamente testado comparando relógios atômicos no solo e a bordo de satélites em órbita; para um relato de efeitos relativísticos, veja Ashby 2002 e Ashby 2003
- ↑ Stairs 2003 e Kramer 2004
- ↑ Visões gerais podem ser encontradas na seção 2.1. de Will 2006; Will 2003, pp. 32–36; Ohanian & Ruffini 1994, seção 4.2
- ↑ Ohanian & Ruffini 1994, pp. 164–172
- ↑ Cf. Kennefick 2005 para as primeiras medidas clássicas das expedições de Arthur Eddington. Para obter uma visão geral das medições mais recentes, consulte Ohanian & Ruffini 1994, ch. 4.3. Para observações modernas diretas mais precisas usando quasares, cf. Shapiro et al. 2004
- ↑ Este não é um axioma independente; pode ser derivado das equações de Einstein e da função lagrangiana de Maxwell usando uma aproximação WKB, cf. Ehlers 1973, sec. 5
- ↑ Blanchet 2006, sec. 1.3
- ↑ Rindler 2001, sec. 1.16; para exemplos históricos, Israel 1987, pp. 202–204; na verdade, Einstein publicou uma dessas derivações em Einstein 1907. Tais cálculos supõem tacitamente que a geometria do espaço é euclidiana, cf. Ehlers & Rindler 1997
- ↑ Do ponto de vista da teoria de Einstein, essas derivações levam em conta o efeito da gravidade no tempo, mas não suas consequências para a deformação do espaço, cf. Rindler 2001, sec. 11.11
- ↑ Para o campo gravitacional do Sol usando sinais de radar refletidos de planetas como Vênus e Mercúrio, cf. cf. Shapiro 1964, Weinberg 1972, ch. 8, sec. 7; para sinais ativamente enviados de volta por sondas espaciais (medições de transponder), cf. Bertotti, Iess & Tortora 2003; para uma visão geral, consulte Ohanian & Ruffini 1994, table 4.4 on p. 200; para medições mais recentes usando sinais recebidos de um pulsar que é parte de um sistema binário, o campo gravitacional causando o atraso de tempo sendo aquele do outro pulsar, cf. Stairs 2003, sec. 4.4
- ↑ Will 1993, sec. 7.1 e 7.2
- ↑ Einstein, A (junho de 1916). «Näherungsweise Integration der Feldgleichungen der Gravitation». Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin. parte 1 (688–696). Bibcode:1916SPAW.......688E
- ↑ Einstein, A (1918). «Über Gravitationswellen». Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin. parte 1 (154–167). Bibcode:1918SPAW.......154E
- ↑ Overbye, Dennis (11 de fevereiro de 2016). «Gravitational Waves Detected, Confirming Einstein's Theory». The New York Times (em inglês). Consultado em 9 de junho de 2019
- ↑ a b Castelvecchi, Davide; Witze, Witze (11 de fevereiro de 2016). «Einstein's gravitational waves found at last». Nature News. doi:10.1038/nature.2016.19361. Consultado em 9 de junho de 2019
- ↑ a b Abbott, B. P. (2016). «Observation of Gravitational Waves from a Binary Black Hole Merger». Physical Review Letters. 116 (6). 061102 páginas. Bibcode:2016PhRvL.116f1102A. PMID 26918975. arXiv:1602.03837
 . doi:10.1103/PhysRevLett.116.061102
. doi:10.1103/PhysRevLett.116.061102
- ↑ a b «Gravitational waves detected 100 years after Einstein's prediction». NSF - National Science Foundation (em inglês). 11 de fevereiro de 2016. Consultado em 9 de junho de 2019
- ↑ Os livros didáticos mais avançados sobre a relatividade geral contêm uma descrição dessas propriedades, por exemplo Schutz 1985, ch. 9
- ↑ Por exemplo Jaranowski & Królak 2005
- ↑ Rindler 2001, ch. 13
- ↑ Gowdy 1971, Gowdy 1974
- ↑ Veja Lehner 2002 para uma breve introdução aos métodos da relatividade numérica, e Seidel 1998 para a conexão com astronomia de ondas gravitacionais
- ↑ Schutz 2003, pp. 48–49, Pais 1982, pp. 253–254
- ↑ Rindler 2001, sec. 11.9
- ↑ Will 1993, pp. 177–181
- ↑ Em consequência, no formalismo pós-newtoniano parametrizado (PPN), as medidas desse efeito determinam uma combinação linear dos termos β e γ, cf. Will 2006, sec. 3.5 e Will 1993, sec. 7.3
- ↑ As medições mais precisas são as de VLBI (Interferometria de Longa Linha de Base) de posições planetárias; veja Will 1993, ch. 5, Will 2006, sec. 3.5, Anderson et al. 1992; para uma visão geral, Ohanian & Ruffini 1994, pp. 406–407
- ↑ Kramer et al. 2006
- ↑ Dediu, Adrian-Horia; Magdalena, Luis; Martín-Vide, Carlos (2015). Theory and Practice of Natural Computing (em inglês). Nova Iorque: Springer. p. 141. ISBN 978-3-319-26841-5
- ↑ Uma imagem que inclui barras de erro é a figura 7 em Will 2006, seção 5.1
- ↑ Stairs 2003, Schutz 2003, pp. 317–321, Bartusiak 2000, pp. 70–86
- ↑ Weisberg & Taylor 2003; para a descoberta do pulsar, veja Hulse & Taylor 1975; para a evidência inicial da radiação gravitacional, veja Taylor 1994
- ↑ Kramer 2004
- ↑ Penrose 2004, §14.5, Misner, Thorne & Wheeler 1973, §11.4
- ↑ Weinberg 1972, sec. 9.6, Ohanian & Ruffini 1994, sec. 7.8
- ↑ Bertotti, Ciufolini & Bender 1987, Nordtvedt 2003
- ↑ Kahn 2007
- ↑ Uma descrição da missão pode ser encontrada em Everitt et al. 2001; uma primeira avaliação pós-voo é apresentada em Everitt, Parkinson & Kahn 2007; mais atualizações estão disponíveis no site da missão: Kahn 1996–2012.
- ↑ Townsend 1997, sec. 4.2.1, Ohanian & Ruffini 1994, pp. 469–471
- ↑ Ohanian & Ruffini 1994, sec. 4.7, Weinberg 1972, sec. 9.7; para uma revisão mais recente, consulte Schäfer 2004
- ↑ Ciufolini & Pavlis 2004, Ciufolini, Pavlis & Peron 2006, Iorio 2009
- ↑ Iorio L. (agosto de 2006). «COMMENTS, REPLIES AND NOTES: A note on the evidence of the gravitomagnetic field of Mars». Classical and Quantum Gravity. 23 (17): 5451–5454. Bibcode:2006CQGra..23.5451I. arXiv:gr-qc/0606092
 . doi:10.1088/0264-9381/23/17/N01
. doi:10.1088/0264-9381/23/17/N01
- ↑ Iorio L. (junho de 2010). «On the Lense–Thirring test with the Mars Global Surveyor in the gravitational field of Mars». Central European Journal of Physics. 8 (3): 509–513. Bibcode:2010CEJPh...8..509I. arXiv:gr-qc/0701146
 . doi:10.2478/s11534-009-0117-6
. doi:10.2478/s11534-009-0117-6
- ↑ Para visões gerais de lentes gravitacionais e suas aplicações, veja Ehlers, Falco & Schneider 1992 e Wambsganss 1998
- ↑ Para uma simples derivação, veja Schutz 2003, ch. 23; cf. Narayan & Bartelmann 1997, sec. 3
- ↑ Walsh, Carswell & Weymann 1979
- ↑ Imagens de todas as lentes conhecidas podem ser encontradas nas páginas do projeto CASTLES, Kochanek et al. 2007
- ↑ Roulet & Mollerach 1997
- ↑ Narayan & Bartelmann 1997, sec. 3.7
- ↑ Barish 2005, Bartusiak 2000, Blair & McNamara 1997
- ↑ Hough & Rowan 2000
- ↑ Hobbs, George; Archibald, A.; Arzoumanian, Z.; Backer, D.; Bailes, M.; Bhat, N. D. R.; Burgay, M.; Burke-Spolaor, S.; et al. (2010). «The international pulsar timing array project: using pulsars as a gravitational wave detector». Classical and Quantum Gravity. 27 (8). 084013 páginas. Bibcode:2010CQGra..27h4013H. arXiv:0911.5206
 . doi:10.1088/0264-9381/27/8/084013
. doi:10.1088/0264-9381/27/8/084013
- ↑ Danzmann & Rüdiger 2003
- ↑ «LISA Pathfinder». Agência Espacial Européia (em inglês). Consultado em 31 de julho de 2019
- ↑ Thorne 1995
- ↑ Cutler & Thorne 2002
- ↑ Miller 2002, palestras 19 e 21
- ↑ Celotti, Miller & Sciama 1999, sec. 3
- ↑ Springel et al. 2005 e o resumo que acompanha Gnedin 2005
- ↑ Blandford 1987, sec. 8.2.4
- ↑ Para o mecanismo básico, veja Carroll & Ostlie 1996, sec. 17.2; para mais sobre os diferentes tipos de objetos astronômicos associados a este, cf. Robson 1996
- ↑ Para uma revisão, consulte Begelman, Blandford & Rees 1984. Para um observador distante, alguns desses jatos parecem mover-se mais rapidamente que a luz; isso, no entanto, pode ser explicado como uma ilusão de ótica que não viola os princípios da relatividade, veja Rees 1966
- ↑ Para estados finais estelares, cf. Oppenheimer & Snyder 1939 ou, para trabalhos numéricos mais recentes, Font 2003, sec. 4.1; para supernovas, ainda há grandes problemas a serem resolvidos, cf. Buras et al. 2003; para simular acreção e a formação de jatos, confira Font 2003, sec. 4.2. Além disso, acredita-se que os efeitos de lentes relativísticas desempenham um papel nos sinais recebidos dos pulsares de raios X, cf. Kraus 1998
- ↑ A evidência inclui limites de compacidade a partir da observação de fenômenos guiados por acreção ("limite de Eddington"), veja Celotti, Miller & Sciama 1999, observações da dinâmica estelar no centro da nossa galáxia Via Láctea, cf. Schödel et al. 2003, e indicações de que pelo menos alguns dos objetos compactos em questão parecem não ter nenhuma superfície sólida, o que pode ser deduzido a partir do exame de explosões de raios X para as quais o objeto central compacto é uma estrela de nêutrons ou um buraco negro, cf. Remillard et al. 2006 para uma visão geral, Narayan 2006, sec. 5. Observações da "sombra" do horizonte central de buracos negros da Via Láctea são ansiosamente procuradas, cf. Falcke, Melia & Agol 2000
- ↑ Dalal et al. 2006
- ↑ Barack & Cutler 2004
- ↑ Originalmente, Einstein 1917; cf. Pais 1982, pp. 285–288
- ↑ Carroll 2001, ch. 2
- ↑ Bergström & Goobar 2003, ch. 9–11; o uso desses modelos é justificado pelo fato de que, em grandes escalas de cerca de cem milhões de anos-luz ou mais, nosso próprio universo realmente parece ser isotrópico e homogêneo, cf. Peebles et al. 1991
- ↑ Por exemplo, com dados WMAP, consulte Spergel et al. 2003
- ↑ Estes testes envolvem observações separadas detalhadas mais adiante; veja, por exemplo, a figura 2 em Bridle et al. 2003
- ↑ Peebles 1966; para um relato recente das previsões, consulte Coc, Vangioni‐Flam et al. 2004; um relato acessível pode ser encontrado em Weiss 2006; comparar com as observações em Olive & Skillman 2004, Bania, Rood & Balser 2002, O'Meara et al. 2001, e Charbonnel & Primas 2005
- ↑ Lahav & Suto 2004, Bertschinger 1998, Springel et al. 2005
- ↑ Alpher & Herman 1948, para uma introdução pedagógica, consulte Bergström & Goobar 2003, ch. 11; para a detecção inicial, consulte Penzias & Wilson 1965 e, para medições de precisão por observatórios de satélite, Mather et al. 1994 (COBE) e Bennett et al. 2003 (WMAP). Medidas futuras também podem revelar evidências sobre ondas gravitacionais no universo primitivo; esta informação adicional está contida na polarização da radiação de fundo, cf. Kamionkowski, Kosowsky & Stebbins 1997 e Seljak & Zaldarriaga 1997
- ↑ A evidência disso vem da determinação de parâmetros cosmológicos e de observações adicionais envolvendo a dinâmica de galáxias e aglomerados de galáxias; cf. Peebles 1993, ch. 18, evidência de lentes gravitacionais, cf. Peacock 1999, sec. 4.6, e simulações de formação de estruturas em larga escala, consulte Springel et al. 2005
- ↑ Peacock 1999, ch. 12, Peskin 2007; em particular, as observações indicam que quase uma parte desprezível dessa matéria não está na forma das partículas elementares usuais ("matéria não bariônica"), cf. Peacock 1999, ch. 12
- ↑ Isto é, alguns físicos questionaram se a evidência para a matéria escura representa, de fato, evidência de desvios da descrição einsteiniana (e newtoniana) da gravidade, cf. uma visão geral está em Mannheim 2006, sec. 9
- ↑ Carroll 2001; uma visão geral acessível é fornecida em Caldwell 2004. Também aqui os cientistas argumentaram que a evidência indica não uma nova forma de energia, mas a necessidade de modificações em nossos modelos cosmológicos, cf. Mannheim 2006, sec. 10; as modificações acima mencionadas não precisam ser modificações da relatividade geral; elas podem, por exemplo, ser modificações na maneira como tratamos as inomogeneidades no universo cf. Buchert 2008
- ↑ Uma boa introdução é Linde 2005; para uma revisão mais recente, consulte Linde 2006
- ↑ Mais precisamente, esses são o problema da planicidade, o problema do horizonte e o problema do monopolo; uma introdução pedagógica pode ser encontrada em Narlikar 1993, sec. 6.4, veja também Börner 1993, sec. 9.1
- ↑ Spergel et al. 2007, sec. 5,6
- ↑ Mais concretamente, a função potencial que é crucial para determinar a dinâmica do ínflaton é simplesmente postulada, mas não derivada de uma teoria física subjacente
- ↑ Brandenberger 2008, sec. 2
- ↑ Gödel 1949
- ↑ Frauendiener 2004, Wald 1984, sec. 11.1, Hawking & Ellis 1973, sec. 6.8, 6.9
- ↑ Wald 1984, sec. 9.2–9.4 e Hawking & Ellis 1973, ch. 6
- ↑ Thorne 1972; para estudos numéricos mais recentes, consulte Berger 2002, sec. 2.1
- ↑ Israel 1987. Uma descrição matemática mais exata distingue vários tipos de horizonte, principalmente horizontes de eventos e horizontes aparentes, cf. Hawking & Ellis 1973, pp. 312–320 ou Wald 1984, sec. 12.2; também existem definições mais intuitivas para sistemas isolados que não requerem conhecimento das propriedades do espaço-tempo no infinito, cf. Ashtekar & Krishnan 2004
- ↑ Para os primeiros passos, cf. Israel 1971; veja Hawking & Ellis 1973, sec. 9.3 ou Heusler 1996, ch. 9 e 10 para uma derivação, e Heusler 1998 assim como Beig & Chruściel 2006 como visões gerais de resultados mais recentes
- ↑ As leis da mecânica dos buracos negros foram descritas pela primeira vez em Bardeen, Carter & Hawking 1973; uma apresentação mais pedagógica pode ser encontrada em Carter 1979; para uma revisão mais recente, consulte Wald 2001, ch. 2. Uma introdução completa, em tamanho de livro, incluindo uma introdução à matemática necessária Poisson 2004. Para o processo Penrose, consulte Penrose 1969
- ↑ Bekenstein 1973, Bekenstein 1974
- ↑ O fato de os buracos negros irradiarem, quantum mecanicamente, foi derivado pela primeira vez em Hawking 1975; uma derivação mais completa pode ser encontrada em Wald 1975. Uma revisão é apresentada em Wald 2001, ch. 3
- ↑ Narlikar 1993, sec. 4.4.4, 4.4.5
- ↑ Horizontes: cf. Rindler 2001, sec. 12.4. Efeito Unruh: Unruh 1976, cf. Wald 2001, ch. 3
- ↑ Hawking & Ellis 1973, sec. 8.1, Wald 1984, sec. 9.1
- ↑ Townsend 1997, ch. 2; um tratamento mais extenso dessa solução pode ser encontrado em Chandrasekhar 1983, ch. 3
- ↑ Townsend 1997, ch. 4; para um tratamento mais extenso, cf. Chandrasekhar 1983, ch. 6
- ↑ Ellis & Van Elst 1999; um olhar mais atento à própria singularidade é levado em consideração em Börner 1993, sec. 1.2
- ↑ Devemos lembrar aqui o fato bem conhecido de que as importantes singularidades "quase-ópticas" das chamadas aproximações eikonais de muitas equações de onda, nomeadamente as "cáusticas", são resolvidas em picos finitos além dessa aproximação.
- ↑ Ou seja, quando há superfícies nulas presas, cf. Penrose 1965
- ↑ Hawking 1966
- ↑ A conjectura foi feita em Belinskii, Khalatnikov & Lifschitz 1971; para uma revisão mais recente, consulte Berger 2002. Uma exposição acessível é dada por Garfinkle 2007
- ↑ A restrição às singularidades futuras exclui naturalmente as singularidades iniciais, como a singularidade do Big Bang, que em princípio são visíveis aos observadores posteriormente no tempo cósmico. A conjectura da censura cósmica foi apresentada pela primeira vez em Penrose 1969; um relato no nível de livro é fornecido em Wald 1984, pp. 302–305. Para resultados numéricos, consulte a revisão Berger 2002, sec. 2.1
- ↑ Hawking & Ellis 1973, sec. 7.1
- ↑ Arnowitt, Deser & Misner 1962; para uma introdução pedagógica, consulte Misner, Thorne & Wheeler 1973, §21.4–§21.7
- ↑ Fourès-Bruhat 1952 e Bruhat 1962; para uma introdução pedagógica, consulte Wald 1984, ch. 10; uma revisão on-line pode ser encontrada em Reula 1998
- ↑ Gourgoulhon 2007; para uma revisão dos conceitos básicos da relatividade numérica, incluindo os problemas decorrentes das peculiaridades das equações de Einstein, consulte Lehner 2001
- ↑ Misner, Thorne & Wheeler 1973, §20.4
- ↑ Arnowitt, Deser & Misner 1962
- ↑ Komar 1959; para uma introdução pedagógica, consulte Wald 1984, sec. 11.2; embora definido de uma maneira totalmente diferente, pode ser demonstrado que é equivalente à massa ADM para espaços-tempo estacionários, cf. Ashtekar & Magnon-Ashtekar 1979
- ↑ Para uma introdução pedagógica, consulte Wald 1984, sec. 11.2
- ↑ Wald 1984, p. 295 e suas referências; isso é importante para questões de estabilidade – se houvesse estados de massa negativos, o espaço Minkowski plano e vazio, que tem massa zero, poderia evoluir para esses estados
- ↑ Townsend 1997, ch. 5
- ↑ Essas definições de energia de massa quase–local são a energia de Hawking, a energia de Geroch ou o momento de energia quase-local de Penrose, baseado em métodos de torção; cf. o artigo de revisão Szabados 2004
- ↑ Uma visão geral da teoria quântica pode ser encontrada em livros-padrão, como Messiah 1999; um relato mais elementar é apresentado em Hey & Walters 2003
- ↑ Ramond 1990, Weinberg 1995, Peskin & Schroeder 1995; uma visão geral mais acessível esta em Auyang 1995
- ↑ Wald 1994, Birrell & Davies 1984
- ↑ Para mais radiação Hawking, veja Hawking 1975 e Wald 1975; uma introdução acessível à evaporação de buraco negro pode ser encontrada em Traschen 2000
- ↑ Wald 2001, ch. 3
- ↑ Simplificando, a matéria é a fonte da curvatura do espaço-tempo e, uma vez que ela possui propriedades quânticas, podemos esperar que o espaço-tempo as tenha também. Cf. Carlip 2001, sec. 2
- ↑ Schutz 2003, p. 407
- ↑ a b Hamber 2009
- ↑ Uma linha do tempo e uma visão geral podem ser encontradas em Rovelli 2000
- ↑ 't Hooft & Veltman 1974
- ↑ Donoghue 1995
- ↑ Em particular, uma técnica perturbativa conhecida como renormalização, parte integrante das previsões derivadas que levam em consideração as contribuições de maior energia, cf. Weinberg 1996, ch. 17, 18, falha neste caso; cf. Veltman 1975, Goroff & Sagnotti 1985; Para uma revisão abrangente e recente da falha da renormalizabilidade perturbativa da gravidade quântica, consulte Hamber 2009
- ↑ Uma introdução acessível no nível de graduação pode ser encontrada em Zwiebach 2004; visões gerais mais completas podem ser encontradas em Polchinski 1998a e Polchinski 1998b
- ↑ Nas energias alcançadas nas experiências atuais, essas cordas são indistinguíveis de partículas pontuais, mas, crucialmente, diferentes modos de oscilação de uma e o mesmo tipo de corda fundamental aparecem como partículas com cargas diferentes (elétricas e outras), por exemplo Ibanez 2000. A teoria é bem sucedida, pois um modo sempre corresponderá a um gráviton, a partícula mensageira da gravidade, por exemplo Green, Schwarz & Witten 1987, sec. 2.3, 5.3
- ↑ Green, Schwarz & Witten 1987, sec. 4.2
- ↑ Weinberg 2000, ch. 31
- ↑ Townsend 1996, Duff 1996
- ↑ Kuchař 1973, sec. 3
- ↑ Essas variáveis representam a gravidade geométrica usando análogos matemáticos de campos elétricos e magnéticos; cf. Ashtekar 1986, Ashtekar 1987
- ↑ Para uma visão, veja Thiemann 2007; contas mais extensas podem ser encontradas em Rovelli 1998, Ashtekar & Lewandowski 2004 bem como nas notas da palestra Thiemann 2003
- ↑ Isham 1994, Sorkin 1997
- ↑ Loll 1998
- ↑ Sorkin 2005
- ↑ Penrose 2004, ch. 33 e as referências nela
- ↑ Hawking 1987
- ↑ Ashtekar 2007, Schwarz 2007
- ↑ Cf. Maddox 1998, pp. 52–59 e 98–122; Penrose 2004, seção 34.1 e capítulo 30.
- ↑ Nieto 2006.
- ↑ Friedrich 2005
- ↑ Para uma análise dos diversos problemas e as técnicas desenvolvidas para superá-los, consulte Lehner 2002.
- ↑ Veja Bartusiak 2000 para um relato até 2000; notícias atualizadas podem ser encontradas nos sites que investigam as colaborações mais importantes tais como GEO 600 Arquivado em 18 de fevereiro de 2007, no Wayback Machine. e LIGO.
- ↑ Para estudos científicos mais recentes sobre as polarizações das ondas gravitacionais de binários compactos, consulte Blanchet et al. 2008, e Arun et al. 2007; para uma revisão do trabalho em binários compactos, consulte Blanchet 2006 e Futamase & Itoh 2006; para uma revisão geral dos testes experimentais da relatividade geral, consulte Will 2006.
- ↑ Veja, por exemplo, o periódico Living Reviews in Relativity.
- ↑ Rini, Matteo (4 de dezembro de 2018). «Satellite Mishap Provides Chance for Relativity Test» (em inglês). American Physical Society. Consultado em 9 de dezembro de 2018
Bibliografia
- Alpher, R. A.; Herman, R. C. (1948). «Evolution of the universe». Nature. 162 (4124): 774–775. Bibcode:1948Natur.162..774A. doi:10.1038/162774b0
- Anderson, J. D.; Campbell, J. K.; Jurgens, R. F.; Lau, E. L. (1992). Sato, H.; Nakamura, T., eds. «Proceedings of the Sixth Marcel Großmann Meeting on General Relativity». World Scientific: 353–355. ISBN 978-981-02-0950-6
- Arnold, V. I. (1989). Mathematical Methods of Classical Mechanics. [S.l.]: Springer. ISBN 978-3-540-96890-0
- Arnowitt, Richard; Stanley, Deser; Misner, Charles W. (1962). Witten, Louis, ed. Gravitation: An Introduction to Current Research. [S.l.]: Wiley. pp. 227–265
- Arun, K.G.; Blanchet, L.; Iyer, B. R.; Qusailah, M. S. S. (2008). «Inspiralling compact binaries in quasi-elliptical orbits: The complete 3PN energy flux». Physical Review D. 77 (6). 064035 páginas. Bibcode:2008PhRvD..77f4035A. doi:10.1103/PhysRevD.77.064035. Arxiv
- Ashby, Neil (2002). «Relativity and the Global Positioning System» (PDF). Physics Today. 55 (5): 41–47. Bibcode:2002PhT....55e..41A. doi:10.1063/1.1485583
- —— (2003). «Relativity in the Global Positioning System». Living Reviews in Relativity. 6 (1). 1 páginas. Bibcode:2003LRR.....6....1A. PMC 5253894
 . PMID 28163638. doi:10.12942/lrr-2003-1. Cópia arquivada em 4 de julho de 2007
. PMID 28163638. doi:10.12942/lrr-2003-1. Cópia arquivada em 4 de julho de 2007
- Ashtekar, Abhay (1986). «New variables for classical and quantum gravity». Phys. Rev. Lett. 57 (18): 2244–2247. Bibcode:1986PhRvL..57.2244A. PMID 10033673. doi:10.1103/PhysRevLett.57.2244
- —— (1987). «New Hamiltonian formulation of general relativity». Phys. Rev. D36 (6): 1587–1602. Bibcode:1987PhRvD..36.1587A. PMID 9958340. doi:10.1103/PhysRevD.36.1587
- —— (2007). «Loop Quantum Gravity: Four Recent Advances and a Dozen Frequently Asked Questions». The Eleventh Marcel Grossmann Meeting - on Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories – Proceedings of the MG11 Meeting on General Relativity. 126 páginas. Bibcode:2008mgm..conf..126A. ISBN 978-981-283-426-3. arXiv:0705.2222
 . doi:10.1142/9789812834300_0008
. doi:10.1142/9789812834300_0008
- ——; Badri, Krishnan (2004). «Isolated and Dynamical Horizons and Their Applications». Living Reviews in Relativity. 7 (1). 10 páginas. Bibcode:2004LRR.....7...10A. PMC 5253930
 . PMID 28163644. arXiv:gr-qc/0407042
. PMID 28163644. arXiv:gr-qc/0407042 . doi:10.12942/lrr-2004-10
. doi:10.12942/lrr-2004-10
- ——; Lewandowski, Jerzy (2004). «Background Independent Quantum Gravity: A Status Report». Class. Quantum Grav. 21 (15): R53–R152. Bibcode:2004CQGra..21R..53A. arXiv:gr-qc/0404018
 . doi:10.1088/0264-9381/21/15/R01
. doi:10.1088/0264-9381/21/15/R01
- ——; Magnon-Ashtekar, Anne (1979). «On conserved quantities in general relativity». Journal of Mathematical Physics. 20 (5): 793–800. Bibcode:1979JMP....20..793A. doi:10.1063/1.524151
- Auyang, Sunny Y. (1995). How is Quantum Field Theory Possible?. Oxford: Oxford University Press. ISBN 978-0-19-509345-2
- Bania, T. M.; Rood, R. T.; Balser, D. S. (2002). «The cosmological density of baryons from observations of 3He+ in the Milky Way». Nature. 415 (6867): 54–57. Bibcode:2002Natur.415...54B. PMID 11780112. doi:10.1038/415054a
- Barack, Leor; Curt, Cutler (2004). «LISA Capture Sources: Approximate Waveforms, Signal-to-Noise Ratios, and Parameter Estimation Accuracy». Phys. Rev. D69 (8). 082005 páginas. Bibcode:2004PhRvD..69h2005B. arXiv:gr-qc/0310125
 . doi:10.1103/PhysRevD.69.082005
. doi:10.1103/PhysRevD.69.082005
- Bardeen, J. M.; Carter, B. (1973). «The Four Laws of Black Hole Mechanics». Comm. Math. Phys. 31 (2): 161–170. Bibcode:1973CMaPh..31..161B. doi:10.1007/BF01645742
- Barish, Barry (2005). Florides, P.; Nolan, B.; Ottewil, A., eds. General Relativity and Gravitation. Proceedings of the 17th International Conference. [S.l.]: World Scientific. pp. 24–34. Bibcode:2005grg..conf.....F. ISBN 978-981-256-424-5
- Barstow, M; Bond, Howard E.; Holberg, J. B.; Burleigh, M. R.; Hubeny, I.; Koester, D. (2005). «Hubble Space Telescope Spectroscopy of the Balmer lines in Sirius B». Mon. Not. R. Astron. Soc. 362 (4): 1134–1142. Bibcode:2005MNRAS.362.1134B. arXiv:astro-ph/0506600
 . doi:10.1111/j.1365-2966.2005.09359.x
. doi:10.1111/j.1365-2966.2005.09359.x
- Bartusiak, Marcia (2000). Einstein's Unfinished Symphony: Listening to the Sounds of Space-Time. Berkley: Joseph Henry Press. ISBN 978-0-425-18620-6
- Begelman, Mitchell C.; Roger D., Blandford; Rees, Martin J. (1984). «Theory of extragalactic radio sources». Rev. Mod. Phys. 56 (2): 255–351. Bibcode:1984RvMP...56..255B. doi:10.1103/RevModPhys.56.255
- Beig, Robert; Chruściel, Piotr T. (2006). Françoise, J.-P.; Naber, G.; Tsou, T.S., eds. Encyclopedia of Mathematical Physics, Volume 2. [S.l.]: Elsevier. p. 2041. Bibcode:2005gr.qc.....2041B. ISBN 978-0-12-512660-1. arXiv:gr-qc/0502041

- Bekenstein, Jacob D. (1973). «Black Holes and Entropy». Phys. Rev. D7 (8): 2333–2346. Bibcode:1973PhRvD...7.2333B. doi:10.1103/PhysRevD.7.2333
- —— (1974). «Generalized Second Law of Thermodynamics in Black-Hole Physics». Phys. Rev. D9 (12): 3292–3300. Bibcode:1974PhRvD...9.3292B. doi:10.1103/PhysRevD.9.3292
- Belinskii, V. A.; Khalatnikov, I. M.; Lifschitz, E. M. (1971). «Oscillatory approach to the singular point in relativistic cosmology». Advances in Physics. 19 (80): 525–573. Bibcode:1970AdPhy..19..525B. doi:10.1080/00018737000101171; artigo original em russo: Belinskii, V. A.; Lifshits, I. M.; Khalatnikov, E. M. (1970). «Колебательный Режим Приближения К Особой Точке В Релятивистской Космологии». Uspekhi Fizicheskikh Nauk (Успехи Физических Наук). 102 (11): 463–500. Bibcode:1970UsFiN.102..463B. doi:10.3367/ufnr.0102.197011d.0463
- Bennett, C. L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S. S.; Page, L.; Spergel, D. N. (2003). «First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results». Astrophys. J. Suppl. Ser. 148 (1): 1–27. Bibcode:2003ApJS..148....1B. arXiv:astro-ph/0302207
 . doi:10.1086/377253
. doi:10.1086/377253
- Berger, Beverly K. (2002). «Numerical Approaches to Spacetime Singularities». Living Reviews in Relativity. 5 (1). 1 páginas. Bibcode:2002LRR.....5....1B. PMC 5256073
 . PMID 28179859. arXiv:gr-qc/0201056
. PMID 28179859. arXiv:gr-qc/0201056 . doi:10.12942/lrr-2002-1
. doi:10.12942/lrr-2002-1
- Bergström, Lars; Goobar, Ariel (2003). Cosmology and Particle Astrophysics. [S.l.]: Wiley & Sons. ISBN 978-3-540-43128-2. (pede registo (ajuda))
- Bertotti, Bruno; Ciufolini, Ignazio; Bender, Peter L. (1987). «New test of general relativity: Measurement of de Sitter geodetic precession rate for lunar perigee». Physical Review Letters. 58 (11): 1062–1065. Bibcode:1987PhRvL..58.1062B. PMID 10034329. doi:10.1103/PhysRevLett.58.1062
- ——; Iess, L.; Tortora, P. (2003). «A test of general relativity using radio links with the Cassini spacecraft». Nature. 425 (6956): 374–376. Bibcode:2003Natur.425..374B. PMID 14508481. doi:10.1038/nature01997
- Bertschinger, Edmund (1998). «Simulations of structure formation in the universe». Annu. Rev. Astron. Astrophys. 36 (1): 599–654. Bibcode:1998ARA&A..36..599B. doi:10.1146/annurev.astro.36.1.599
- Birrell, N. D.; Davies, P. C. (1984). Quantum Fields in Curved Space. Cambridge: Cambridge University Press. ISBN 978-0-521-27858-4
- Blair, David (1997). Ripples on a Cosmic Sea. The Search for Gravitational Waves. [S.l.]: Perseus. ISBN 978-0-7382-0137-5
- Blanchet, Luc; Faye, G.; Iyer, B. R.; Sinha, S. (2008). «The third post-Newtonian gravitational wave polarisations and associated spherical harmonic modes for inspiralling compact binaries in quasi-circular orbits». Classical and Quantum Gravity. 25 (16). 165003 páginas. Arxiv
- —— (2006). «Gravitational Radiation from Post-Newtonian Sources and Inspiralling Compact Binaries». Living Rev. Relativity. 9 (1). 4 páginas. Bibcode:2006LRR.....9....4B. PMC 5255899
 . PMID 28179874. doi:10.12942/lrr-2006-4
. PMID 28179874. doi:10.12942/lrr-2006-4
- Blandford, Roger (1987). Hawking, Stephen W.; Israel, Werner, eds. 300 Years of Gravitation. Cambridge: Cambridge University Press. pp. 277–329. ISBN 978-0-521-37976-2
- Börner, Gerhard (1993). The Early Universe. Facts and Fiction. [S.l.]: Springer. ISBN 978-0-387-56729-7
- Brandenberger, Robert H. (2008). «Conceptual Problems of Inflationary Cosmology and a New Approach to Cosmological Structure Formation». Inflationary Cosmology. Lecture Notes in Physics. 738: 393–424. Bibcode:2008LNP...738..393B. ISBN 978-3-540-74352-1. arXiv:hep-th/0701111
 . doi:10.1007/978-3-540-74353-8_11
. doi:10.1007/978-3-540-74353-8_11
- Brans, C. H.; Dicke, R. H. (1961). «Mach's Principle and a Relativistic Theory of Gravitation». Physical Review. 124 (3): 925–935. Bibcode:1961PhRv..124..925B. doi:10.1103/PhysRev.124.925
- Bridle, Sarah L.; Ofer, Lahav; Ostriker, Jeremiah P.; Steinhardt, Paul J. (2003). «Precision Cosmology? Not Just Yet». Science. 299 (5612): 1532–1533. Bibcode:2003Sci...299.1532B. PMID 12624255. arXiv:astro-ph/0303180
 . doi:10.1126/science.1082158
. doi:10.1126/science.1082158
- Bruhat, Yvonne (1962). Gravitation: An Introduction to Current Research. [S.l.]: Wiley. ISBN 978-1-114-29166-9
- Buchert, Thomas (2008). «Dark Energy from Structure—A Status Report». General Relativity and Gravitation. 40 (2–3): 467–527. Bibcode:2008GReGr..40..467B. arXiv:0707.2153
 . doi:10.1007/s10714-007-0554-8
. doi:10.1007/s10714-007-0554-8
- Buras, R.; Rampp, M.; Janka, H.-Th.; Kifonidis, K. (2003). «Improved Models of Stellar Core Collapse and Still no Explosions: What is Missing?». Phys. Rev. Lett. 90 (24). 241101 páginas. Bibcode:2003PhRvL..90x1101B. PMID 12857181. arXiv:astro-ph/0303171
 . doi:10.1103/PhysRevLett.90.241101
. doi:10.1103/PhysRevLett.90.241101
- Caldwell, Robert R. (2004). «Dark Energy». Physics World. 17 (5): 37–42. doi:10.1088/2058-7058/17/5/36
- Carlip, Steven (2001). «Quantum Gravity: a Progress Report». Rep. Prog. Phys. 64 (8): 885–942. Bibcode:2001RPPh...64..885C. arXiv:gr-qc/0108040
 . doi:10.1088/0034-4885/64/8/301
. doi:10.1088/0034-4885/64/8/301
- Carroll, Bradley W.; Ostlie, Dale A. (1996). An Introduction to Modern Astrophysics. [S.l.]: Addison-Wesley. ISBN 978-0-201-54730-6
- Carroll, Sean M. (2001). «The Cosmological Constant». Living Reviews in Relativity. 4 (1). 1 páginas. Bibcode:2001LRR.....4....1C. PMC 5256042
 . PMID 28179856. arXiv:astro-ph/0004075
. PMID 28179856. arXiv:astro-ph/0004075 . doi:10.12942/lrr-2001-1
. doi:10.12942/lrr-2001-1
- Carter, Brandon (1979). Hawking, S. W.; Israel, W., eds. General Relativity, an Einstein Centenary Survey. Cambridge: Cambridge University Press. ISBN 978-0-521-29928-2
- Celotti, Annalisa; Miller, John C.; Sciama, Dennis W. (1999). «Astrophysical evidence for the existence of black holes». Class. Quantum Grav. 16 (12A): A3–A21. Bibcode:1999CQGra..16A...3C. arXiv:astro-ph/9912186
 . doi:10.1088/0264-9381/16/12A/301
. doi:10.1088/0264-9381/16/12A/301
- Chandrasekhar, Subrahmanyan (1983). The Mathematical Theory of Black Holes. Oxford: Oxford University Press. ISBN 978-0-19-850370-5
- —— (1984). «The general theory of relativity - Why 'It is probably the most beautiful of all existing theories'». Journal of Astrophysics and Astronomy. 5: 3–11. Bibcode:1984JApA....5....3C. doi:10.1007/BF02714967
- Charbonnel, C.; Primas, F. (2005). «The Lithium Content of the Galactic Halo Stars». Astronomy & Astrophysics. 442 (3): 961–992. Bibcode:2005A&A...442..961C. arXiv:astro-ph/0505247
 . doi:10.1051/0004-6361:20042491
. doi:10.1051/0004-6361:20042491
- Ciufolini, Ignazio; Pavlis, Erricos C. (2004). «A confirmation of the general relativistic prediction of the Lense-Thirring effect». Nature. 431 (7011): 958–960. Bibcode:2004Natur.431..958C. PMID 15496915. doi:10.1038/nature03007
- ——; Pavlis, Erricos C.; Peron, R. (2006). «Determination of frame-dragging using Earth gravity models from CHAMP and GRACE». New Astron. 11 (8): 527–550. Bibcode:2006NewA...11..527C. doi:10.1016/j.newast.2006.02.001
- Coc, A.; Vangioni‐Flam, Elisabeth; Descouvemont, Pierre; Adahchour, Abderrahim; Angulo, Carmen (2004). «Updated Big Bang Nucleosynthesis confronted to WMAP observations and to the Abundance of Light Elements». Astrophysical Journal. 600 (2): 544–552. Bibcode:2004ApJ...600..544C. arXiv:astro-ph/0309480
 . doi:10.1086/380121
. doi:10.1086/380121
- Cutler, Curt; Thorne, Kip S. (2002). Bishop, Nigel; Maharaj, Sunil D., eds. Proceedings of 16th International Conference on General Relativity and Gravitation (GR16). [S.l.]: World Scientific. Bibcode:2002gr.qc.....4090C. ISBN 978-981-238-171-2. arXiv:gr-qc/0204090

- Dalal, Neal; Holz, Daniel E.; Hughes, Scott A.; Jain, Bhuvnesh (2006). «Short GRB and binary black hole standard sirens as a probe of dark energy». Phys. Rev. D. 74 (6). 063006 páginas. Bibcode:2006PhRvD..74f3006D. arXiv:astro-ph/0601275
 . doi:10.1103/PhysRevD.74.063006
. doi:10.1103/PhysRevD.74.063006
- Danzmann, Karsten; Rüdiger, Albrecht (2003). «LISA Technology—Concepts, Status, Prospects» (PDF). Class. Quantum Grav. 20 (10): S1–S9. Bibcode:2003CQGra..20S...1D. doi:10.1088/0264-9381/20/10/301. hdl:11858/00-001M-0000-0013-5233-E. Cópia arquivada (PDF) em 26 de setembro de 2007
- Dirac, Paul (1996). General Theory of Relativity. Princeton, NJ: Princeton University Press. ISBN 978-0-691-01146-2
- Donoghue, John F. (1995). Cornet, Fernando, ed. Effective Theories: Proceedings of the Advanced School, Almunecar, Spain, 26 June–1 July 1995. Singapura: World Scientific. Bibcode:1995gr.qc....12024D. ISBN 978-981-02-2908-5
- Duff, Michael (1996). «M-Theory (the Theory Formerly Known as Strings)». Int. J. Mod. Phys. A. 11 (32): 5623–5641. Bibcode:1996IJMPA..11.5623D. arXiv:hep-th/9608117
 . doi:10.1142/S0217751X96002583
. doi:10.1142/S0217751X96002583
- Ehlers, Jürgen (1973). Israel, Werner, ed. Relativity, Astrophysics and Cosmology. [S.l.]: D. Reidel. ISBN 978-90-277-0369-9
- ——; Falco, Emilio E.; Schneider, Peter (1992). Gravitational lenses. [S.l.]: Springer. ISBN 978-3-540-66506-9
- ——; Lämmerzahl, Claus, eds. (2006). Special Relativity—Will it Survive the Next 101 Years?. [S.l.]: Springer. ISBN 978-3-540-34522-0
- ——; Rindler, Wolfgang (1997). «Local and Global Light Bending in Einstein's and other Gravitational Theories». General Relativity and Gravitation. 29 (4): 519–529. Bibcode:1997GReGr..29..519E. doi:10.1023/A:1018843001842
- Einstein, Albert (1907). «Über das Relativitätsprinzip und die aus demselben gezogene Folgerungen». Jahrbuch der Radioaktivität und Elektronik. 4. 411 páginas
- —— (1915). «Die Feldgleichungen der Gravitation». Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin: 844–847
- —— (1916). «Die Grundlage der allgemeinen Relativitätstheorie». Annalen der Physik. 49 (7): 769–822. Bibcode:1916AnP...354..769E. doi:10.1002/andp.19163540702
- —— (1916). «Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie». Sitzungsberichte der Preußischen Akademie der Wissenschaften. 142 páginas
- Ellis, George F R; Van Elst, Henk (1999). Lachièze-Rey, Marc, ed. «Theoretical and Observational Cosmology: Cosmological models (Cargèse lectures 1998)». Theoretical and Observational Cosmology : Proceedings of the NATO Advanced Study Institute on Theoretical and Observational Cosmology. 541: 1–116. Bibcode:1999ASIC..541....1E. ISBN 978-0-7923-5946-3. arXiv:gr-qc/9812046
 . doi:10.1007/978-94-011-4455-1_1
. doi:10.1007/978-94-011-4455-1_1
- Engler, Gideon (2002). «Einstein and the most beautiful theories in physics». International Studies in the Philosophy of Science. 16 (1): 27–37. doi:10.1080/02698590120118800
- Everitt, C. W. F.; Buchman, S.; DeBra, D. B.; Keiser, G. M. (2001). Lämmerzahl, C.; Everitt, C. W. F.; Hehl, F. W., eds. Gyros, Clocks, and Interferometers: Testing Relativistic Gravity in Space (Lecture Notes in Physics 562). [S.l.]: Springer. ISBN 978-3-540-41236-6
- ——; Parkinson, Bradford; Kahn, Bob (2007). «The Gravity Probe B experiment. Post Flight Analysis—Final Report (Preface and Executive Summary)» (PDF). Project Report: NASA, Stanford University and Lockheed Martin
- Falcke, Heino; Melia, Fulvio; Agol, Eric (2000). «Viewing the Shadow of the Black Hole at the Galactic Center». Astrophysical Journal. 528 (1): L13–L16. Bibcode:2000ApJ...528L..13F. PMID 10587484. arXiv:astro-ph/9912263
 . doi:10.1086/312423
. doi:10.1086/312423
- Flanagan, Éanna É.; Hughes, Scott A. (2005). «The basics of gravitational wave theory». New J. Phys. 7 (1). 204 páginas. Bibcode:2005NJPh....7..204F. arXiv:gr-qc/0501041
 . doi:10.1088/1367-2630/7/1/204
. doi:10.1088/1367-2630/7/1/204
- Font, José A. (2003). «Numerical Hydrodynamics in General Relativity». Living Reviews in Relativity. 6 (1). 4 páginas. Bibcode:2003LRR.....6....4F. PMC 5660627
 . PMID 29104452. doi:10.12942/lrr-2003-4
. PMID 29104452. doi:10.12942/lrr-2003-4
- Fourès-Bruhat, Yvonne (1952). «Théoréme d'existence pour certains systémes d'équations aux derivées partielles non linéaires». Acta Mathematica. 88 (1): 141–225. Bibcode:1952AcM....88..141F. doi:10.1007/BF02392131
- Frauendiener, Jörg (2004). «Conformal Infinity». Living Reviews in Relativity. 7 (1). 1 páginas. Bibcode:2004LRR.....7....1F. PMC 5256109
 . PMID 28179863. doi:10.12942/lrr-2004-1
. PMID 28179863. doi:10.12942/lrr-2004-1
- Friedrich, Helmut (2005). «Is general relativity 'essentially understood'?». Annalen Phys. 15: 84–108. Bibcode:2006AnP...518...84F. doi:10.1002/andp.200510173
- Futamase, T.; Itoh, Y. (2006). «The Post-Newtonian Approximation for Relativistic Compact Binaries». Living Rev. Relativity. 10 (1). 2 páginas. Bibcode:2007LRR....10....2F. PMC 5255906
 . PMID 28179819. doi:10.12942/lrr-2007-2
. PMID 28179819. doi:10.12942/lrr-2007-2
- Gamow, George (1970). My World Line. [S.l.]: Viking Press. ISBN 978-0-670-50376-6
- Garfinkle, David (2007). «Of singularities and breadmaking». Einstein Online. Cópia arquivada em 10 de agosto de 2007
- Geroch, Robert (1996). «Partial Differential Equations of Physics». General Relativity. 19 páginas. Bibcode:1996gere.conf...19G. arXiv:gr-qc/9602055

- Giulini, Domenico (2005). Special Relativity: A First Encounter. Oxford: Oxford University Press. ISBN 978-0-19-856746-2
- —— (2006). Ehlers, Jürgen; Lämmerzahl, Claus, eds. Special Relativity—Will it Survive the Next 101 Years?. Col: Lecture Notes in Physics. 702. [S.l.]: Springer. p. 45–111. Bibcode:2006math.ph...2018G. ISBN 978-3-540-34522-0. arXiv:math-ph/0602018
 . doi:10.1007/3-540-34523-X_4
. doi:10.1007/3-540-34523-X_4
- —— (2007). Stamatescu, I. O., ed. «An assessment of current paradigms in the physics of fundamental interactions: Some remarks on the notions of general covariance and background independence». Approaches to Fundamental Physics. Lecture Notes in Physics. 721: 105–120. Bibcode:2007LNP...721..105G. ISBN 978-3-540-71115-5. arXiv:gr-qc/0603087
 . doi:10.1007/978-3-540-71117-9_6
. doi:10.1007/978-3-540-71117-9_6
- Gnedin, Nickolay Y. (2005). «Digitizing the Universe». Nature. 435 (7042): 572–573. Bibcode:2005Natur.435..572G. PMID 15931201. doi:10.1038/435572a
- Gödel, Kurt (1949). «An Example of a New Type of Cosmological Solution of Einstein's Field Equations of Gravitation». Rev. Mod. Phys. 21 (3): 447–450. Bibcode:1949RvMP...21..447G. doi:10.1103/RevModPhys.21.447
- Goenner, Hubert F. M. (2004). «On the History of Unified Field Theories». Living Reviews in Relativity. 7 (1). 2 páginas. Bibcode:2004LRR.....7....2G. PMC 5256024
 . PMID 28179864. doi:10.12942/lrr-2004-2
. PMID 28179864. doi:10.12942/lrr-2004-2
- Goroff, Marc H.; Sagnotti, Augusto (1985). «Quantum gravity at two loops». Phys. Lett. 160B (1-3): 81–86. Bibcode:1985PhLB..160...81G. doi:10.1016/0370-2693(85)91470-4
- Gourgoulhon, Eric (2007). «3+1 Formalism and Bases of Numerical Relativity». arXiv:gr-qc/0703035

- Gowdy, Robert H. (1971). «Gravitational Waves in Closed Universes». Phys. Rev. Lett. 27 (12): 826–829. doi:10.1103/PhysRevLett.27.826
- —— (1974). «Vacuum spacetimes with two-parameter spacelike isometry groups and compact invariant hypersurfaces: Topologies and boundary conditions». Annals of Physics. 83 (1): 203–241. Bibcode:1974AnPhy..83..203G. doi:10.1016/0003-4916(74)90384-4
- Green, Michael; Schwarz, J. H.; Witten, E. (1987). Superstring theory. Volume 1: Introduction. Cambridge: Cambridge University Press. ISBN 978-0-521-35752-4
- Greenstein, J. L.; Oke, J. B.; Shipman, H. L. (1971). «Effective Temperature, Radius, and Gravitational Redshift of Sirius B». Astrophysical Journal. 169. 563 páginas. Bibcode:1971ApJ...169..563G. doi:10.1086/151174
- Hamber, Herbert W. (2009). Hamber, Herbert W, ed. Quantum Gravitation - The Feynman Path Integral Approach. [S.l.]: Springer Publishing. ISBN 978-3-540-85292-6. doi:10.1007/978-3-540-85293-3
- Hafele, J. C.; Keating, R. E. (1972). «Around-the-World Atomic Clocks: Predicted Relativistic Time Gains». Science. 177 (4044): 166–168. Bibcode:1972Sci...177..166H. PMID 17779917. doi:10.1126/science.177.4044.166
- ——; Keating, R. E. (1972). «Around-the-World Atomic Clocks: Observed Relativistic Time Gains». Science. 177 (4044): 168–170. Bibcode:1972Sci...177..168H. PMID 17779918. doi:10.1126/science.177.4044.168
- Havas, P. (1964). «Four-Dimensional Formulation of Newtonian Mechanics and Their Relation to the Special and the General Theory of Relativity». Rev. Mod. Phys. 36 (4): 938–965. Bibcode:1964RvMP...36..938H. doi:10.1103/RevModPhys.36.938
- Hawking, Stephen W. (1966). «The occurrence of singularities in cosmology». Proceedings of the Royal Society. A294 (1439): 511–521. Bibcode:1966RSPSA.294..511H. JSTOR 2415489. doi:10.1098/rspa.1966.0221
- —— (1975). «Particle Creation by Black Holes». Communications in Mathematical Physics. 43 (3): 199–220. Bibcode:1975CMaPh..43..199H. doi:10.1007/BF02345020
- —— (1987). Israel, Werner, ed. 300 Years of Gravitation. Cambridge: Cambridge University Press. ISBN 978-0-521-37976-2
- —— (1973). Ellis, George F. R., ed. The large scale structure of space-time. Cambridge: Cambridge University Press. ISBN 978-0-521-09906-6
- Heckmann, O. H. L.; Schücking, E. (1959). «Newtonsche und Einsteinsche Kosmologie». In: Flügge, S. Encyclopedia of Physics. 53. 489 páginas
- Heusler, Markus (1998). «Stationary Black Holes: Uniqueness and Beyond». Living Reviews in Relativity. 1 (1). 6 páginas. Bibcode:1998LRR.....1....6H. PMC 5567259
 . PMID 28937184. doi:10.12942/lrr-1998-6
. PMID 28937184. doi:10.12942/lrr-1998-6
- —— (1996). Black Hole Uniqueness Theorems. Cambridge: Cambridge University Press. ISBN 978-0-521-56735-0
- Hey, Tony; Walters, Patrick (2003). The new quantum universe. Cambridge: Cambridge University Press. Bibcode:2003nqu..book.....H. ISBN 978-0-521-56457-1
- Hough, Jim; Rowan, Sheila (2000). «Gravitational Wave Detection by Interferometry (Ground and Space)». Living Reviews in Relativity. 3 (1). 3 páginas. Bibcode:2000LRR.....3....3R. PMC 5255574
 . PMID 28179855. doi:10.12942/lrr-2000-3
. PMID 28179855. doi:10.12942/lrr-2000-3
- Hubble, Edwin (1929). «A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae» (PDF). Proc. Natl. Acad. Sci. 15 (3): 168–173. Bibcode:1929PNAS...15..168H. PMC 522427
 . PMID 16577160. doi:10.1073/pnas.15.3.168
. PMID 16577160. doi:10.1073/pnas.15.3.168
- Hulse, Russell A.; Taylor, Joseph H. (1975). «Discovery of a pulsar in a binary system». Astrophys. J. 195: L51–L55. Bibcode:1975ApJ...195L..51H. doi:10.1086/181708
- Ibanez, L. E. (2000). «The second string (phenomenology) revolution». Class. Quantum Grav. 17 (5): 1117–1128. Bibcode:2000CQGra..17.1117I. arXiv:hep-ph/9911499
 . doi:10.1088/0264-9381/17/5/321
. doi:10.1088/0264-9381/17/5/321
- Iorio, L. (2009). «An Assessment of the Systematic Uncertainty in Present and Future Tests of the Lense-Thirring Effect with Satellite Laser Ranging». Space Sci. Rev. 148 (1-4): 363–381. Bibcode:2009SSRv..148..363I. arXiv:0809.1373
 . doi:10.1007/s11214-008-9478-1
. doi:10.1007/s11214-008-9478-1
- Isham, Christopher J. (1994). «Prima facie questions in quantum gravity». In: Ehlers, Jürgen; Friedrich, Helmut. Canonical Gravity: From Classical to Quantum. [S.l.]: Springer. ISBN 978-3-540-58339-4
- Israel, Werner (1971). «Event Horizons and Gravitational Collapse». General Relativity and Gravitation. 2 (1): 53–59. Bibcode:1971GReGr...2...53I. doi:10.1007/BF02450518
- —— (1987). «Dark stars: the evolution of an idea». In: Hawking, S. W. 300 Years of Gravitation. Cambridge: Cambridge University Press. pp. 199–276. ISBN 978-0-521-37976-2
- Janssen, Michel (2005). «Of pots and holes: Einstein's bumpy road to general relativity» (PDF). Annalen der Physik. 14 (S1): 58–85. Bibcode:2005AnP...517S..58J. doi:10.1002/andp.200410130
- Jaranowski, Piotr; Królak, Andrzej (2005). «Gravitational-Wave Data Analysis. Formalism and Sample Applications: The Gaussian Case». Living Reviews in Relativity. 8 (1). 3 páginas. Bibcode:2005LRR.....8....3J. PMC 5253919
 . PMID 28163647. doi:10.12942/lrr-2005-3
. PMID 28163647. doi:10.12942/lrr-2005-3
- Kahn, Bob (1996–2012). «Gravity Probe B Website». Stanford University
- —— (14 de abril de 2007). «Was Einstein right? Scientists provide first public peek at Gravity Probe B results» (PDF). Stanford University Press Release. Stanford University News Service
- Kamionkowski, Marc; Kosowsky, Arthur; Stebbins, Albert (1997). «Statistics of Cosmic Microwave Background Polarization». Phys. Rev. D55 (12): 7368–7388. Bibcode:1997PhRvD..55.7368K. arXiv:astro-ph/9611125
 . doi:10.1103/PhysRevD.55.7368
. doi:10.1103/PhysRevD.55.7368
- Kennefick, Daniel (2005). «Astronomers Test General Relativity: Light-bending and the Solar Redshift». In: Renn, Jürgen. One hundred authors for Einstein. [S.l.]: Wiley-VCH. p. 178–181. ISBN 978-3-527-40574-9
- —— (2007). Not Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition. «Proceedings of the 7th Conference on the History of General Relativity, Tenerife, 2005». 0709. 685 páginas. Bibcode:2007arXiv0709.0685K. doi:10.1016/j.shpsa.2012.07.010
- Kenyon, I. R. (1990). General Relativity. Oxford: Oxford University Press. ISBN 978-0-19-851996-6
- Kochanek, C.S.; Falco, E.E.; Impey, C.; Lehar, J. (2007). «CASTLES Survey Website». Harvard-Smithsonian Center for Astrophysics
- Komar, Arthur (1959). «Covariant Conservation Laws in General Relativity». Phys. Rev. 113 (3): 934–936. Bibcode:1959PhRv..113..934K
- Kramer, Michael (2004). Karshenboim, S. G.; Peik, E., eds. «Astrophysics, Clocks and Fundamental Constants: Millisecond Pulsars as Tools of Fundamental Physics». Lecture Notes in Physics. 648: 33–54. Bibcode:2004LNP...648...33K. arXiv:astro-ph/0405178
 . doi:10.1007/978-3-540-40991-5_3
. doi:10.1007/978-3-540-40991-5_3
- ——; Stairs, I. H.; Manchester, R. N.; McLaughlin, M. A.; Lyne, A. G.; Ferdman, R. D.; Burgay, M.; Lorimer, D. R.; Possenti, A. (2006). «Tests of general relativity from timing the double pulsar». Science. 314 (5796): 97–102. Bibcode:2006Sci...314...97K. PMID 16973838. doi:10.1126/science.1132305
- Kraus, Ute (1998). «Light Deflection Near Neutron Stars». Relativistic Astrophysics. [S.l.]: Vieweg. pp. 66–81. ISBN 978-3-528-06909-4
- Kuchař, Karel (1973). «Canonical Quantization of Gravity». In: Israel, Werner. Relativity, Astrophysics and Cosmology. [S.l.]: D. Reidel. pp. 237–288. ISBN 978-90-277-0369-9
- Künzle, H. P. (1972). «Galilei and Lorentz Structures on spacetime: comparison of the corresponding geometry and physics». Annales de l'Institut Henri Poincaré A. 17: 337–362
- Lahav, Ofer; Yasushi, Suto (2004). «Measuring our Universe from Galaxy Redshift Surveys». Living Reviews in Relativity. 7 (1). 8 páginas. Bibcode:2004LRR.....7....8L. PMC 5253994
 . PMID 28163643. arXiv:astro-ph/0310642
. PMID 28163643. arXiv:astro-ph/0310642 . doi:10.12942/lrr-2004-8
. doi:10.12942/lrr-2004-8
- Landau, L. D.; Lifshitz, E. M. (1975). The Classical Theory of Fields, v. 2. [S.l.]: Elsevier Science, Ltd. ISBN 978-0-08-018176-9
- Landgraf, M.; Hechler, M.; Kemble, S. (2005). «Mission design for LISA Pathfinder». Class. Quantum Grav. 22 (10): S487–S492. Bibcode:2005CQGra..22S.487L. arXiv:gr-qc/0411071
 . doi:10.1088/0264-9381/22/10/048
. doi:10.1088/0264-9381/22/10/048
- Lehner, Luis (2001). «Numerical Relativity: A review». Class. Quant. Grav. 18 (17): R25–R86. Bibcode:2001CQGra..18R..25L. doi:10.1088/0264-9381/18/17/202. Arxiv
- —— (2002). «Numerical Relativity: Status and Prospects». General Relativity and Gravitation: Proceedings of the 16th International Conference. 210 páginas. Bibcode:2002grg..conf..210L. ISBN 978-981-238-171-2. doi:10.1142/9789812776556_0010. Arxiv
- Linde, Andrei (2005). «Particle Physics and Inflationary Cosmology». Contemp.concepts Phys. 5: 1–362. Bibcode:2005hep.th....3203L. ISBN 978-3-7186-0489-0. arXiv:hep-th/0503203

- —— (2006). «Towards inflation in string theory». J. Phys. Conf. Ser. 24 (1): 151–160. Bibcode:2005JPhCS..24..151L. arXiv:hep-th/0503195
 . doi:10.1088/1742-6596/24/1/018
. doi:10.1088/1742-6596/24/1/018
- Loll, Renate (1998). «Discrete Approaches to Quantum Gravity in Four Dimensions». Living Reviews in Relativity. 1 (1). 13 páginas. Bibcode:1998LRR.....1...13L. PMC 5253799
 . PMID 28191826. arXiv:gr-qc/9805049
. PMID 28191826. arXiv:gr-qc/9805049 . doi:10.12942/lrr-1998-13
. doi:10.12942/lrr-1998-13
- Lovelock, David (1972). «The Four-Dimensionality of Space and the Einstein Tensor». J. Math. Phys. 13 (6): 874–876. Bibcode:1972JMP....13..874L. doi:10.1063/1.1666069
- Ludyk, Günter (2013). Einstein in Matrix Form 1 ed. Berlim: Springer. ISBN 978-3-642-35797-8
- MacCallum, M. (2006). Mornas, L.; Alonso, J. D., eds. Finding and using exact solutions of the Einstein equations. «AIP Conference Proceedings» (A Century of Relativity Physics: ERE05, the XXVIII Spanish Relativity Meeting). 841: 129–143. Bibcode:2006AIPC..841..129M. doi:10.1063/1.2218172
- Maddox, John (1998). What Remains To Be Discovered. Londres: Macmillan. ISBN 0-684-82292-X
- Mannheim, Philip D. (2006). «Alternatives to Dark Matter and Dark Energy». Prog. Part. Nucl. Phys. 56 (2): 340–445. Bibcode:2006PrPNP..56..340M. arXiv:astro-ph/0505266
 . doi:10.1016/j.ppnp.2005.08.001
. doi:10.1016/j.ppnp.2005.08.001
- Mather, J. C.; Cheng, E. S.; Cottingham, D. A.; Eplee, R. E.; Fixsen, D. J.; Hewagama, T.; Isaacman, R. B.; Jensen, K. A.; Meyer, S. S. (1994). «Measurement of the cosmic microwave spectrum by the COBE FIRAS instrument». Astrophysical Journal. 420: 439–444. doi:10.1086/173574
- Mermin, N. David (2005). It's About Time. Understanding Einstein's Relativity. Princeton, NJ: Princeton University Press. ISBN 978-0-691-12201-4. (pede registo (ajuda))
- Messiah, Albert (1999). Quantum Mechanics. [S.l.]: Dover Publications. ISBN 978-0-486-40924-5
- Miller, Cole (2002). Stellar Structure and Evolution (Lecture notes for Astronomy 606). [S.l.]: University of Maryland
- Misner, Charles W.; Thorne, Kip. S.; Wheeler, John A. (1973). Gravitation. [S.l.]: W. H. Freeman. ISBN 978-0-7167-0344-0
- Møller, Christian (1952). The Theory of Relativity. Oxford: Oxford University Press
- Narayan, Ramesh; Bartelmann, Matthias (1997). «Lectures on Gravitational Lensing». arXiv:astro-ph/9606001

- —— (2006). «Black holes in astrophysics». New Journal of Physics. 7 (1). 199 páginas. Bibcode:2005NJPh....7..199N. arXiv:gr-qc/0506078

- Narlikar, Jayant V. (1993). Introduction to Cosmology. Cambridge: Cambridge University Press. ISBN 978-0-521-41250-6
- Nieto, Michael Martin (2006). «The quest to understand the Pioneer anomaly» (PDF). EurophysicsNews. 37 (6): 30–34. Bibcode:2006ENews..37f..30N. doi:10.1051/epn:2006604. Arquivado do original (PDF) em 29 de junho de 2007
- Nordström, Gunnar (1918). «On the Energy of the Gravitational Field in Einstein's Theory». Verhandl. Koninkl. Ned. Akad. Wetenschap. 26: 1238–1245. Bibcode:1918KNAB...20.1238N
- Nordtvedt, Kenneth (2003). «Lunar Laser Ranging—a comprehensive probe of post-Newtonian gravity». arXiv:gr-qc/0301024

- Norton, John D. (1985). «What was Einstein's principle of equivalence?» (PDF). Studies in History and Philosophy of Science. 16 (3): 203–246. doi:10.1016/0039-3681(85)90002-0
- Ohanian, Hans C.; Ruffini, Remo (1994). Gravitation and Spacetime. [S.l.]: W. W. Norton & Company. ISBN 978-0-393-96501-8
- Olive, K. A.; Skillman, E. A. (2004). «A Realistic Determination of the Error on the Primordial Helium Abundance». Astrophysical Journal. 617 (1): 29–49. Bibcode:2004ApJ...617...29O. doi:10.1086/425170
- O'Meara, John M.; Tytler, David; Kirkman, David; Suzuki, Nao; Prochaska, Jason X.; Lubin, Dan; Wolfe, Arthur M. (2001). «The Deuterium to Hydrogen Abundance Ratio Towards a Fourth QSO: HS0105+1619». Astrophysical Journal. 552 (2): 718–730. Bibcode:2001ApJ...552..718O. arXiv:astro-ph/0011179
 . doi:10.1086/320579
. doi:10.1086/320579
- Oppenheimer, J. Robert; Snyder, H. (1939). «On continued gravitational contraction». Physical Review. 56 (5): 455–459. Bibcode:1939PhRv...56..455O. doi:10.1103/PhysRev.56.455
- Overbye, Dennis (1999). Lonely Hearts of the Cosmos: the story of the scientific quest for the secret of the Universe. [S.l.]: Back Bay. ISBN 978-0-316-64896-7
- Pais, Abraham (1982). 'Subtle is the Lord ...' The Science and life of Albert Einstein. Oxford: Oxford University Press. ISBN 0-19-853907-X
- Peacock, John A. (1999). Cosmological Physics. Cambridge: Cambridge University Press. ISBN 978-0-521-41072-4
- Peebles, P. J. E. (1966). «Primordial Helium abundance and primordial fireball II». Astrophysical Journal. 146: 542–552. Bibcode:1966ApJ...146..542P. doi:10.1086/148918
- —— (1993). Principles of physical cosmology. Princeton, NJ: Princeton University Press. ISBN 978-0-691-01933-8
- ——; Schramm, D. N.; Turner, E. L.; Kron, R. G. (1991). «The case for the relativistic hot Big Bang cosmology». Nature. 352 (6338): 769–776. Bibcode:1991Natur.352..769P. doi:10.1038/352769a0
- Penrose, Roger (1965). «Gravitational collapse and spacetime singularities». Physical Review Letters. 14 (3): 57–59. Bibcode:1965PhRvL..14...57P. doi:10.1103/PhysRevLett.14.57
- —— (1969). «Gravitational collapse: the role of general relativity». Rivista del Nuovo Cimento. 1: 252–276. Bibcode:1969NCimR...1..252P
- —— (2004). The Road to Reality. [S.l.]: A. A. Knopf. ISBN 0-679-45443-8
- Penzias, A. A.; Wilson, R. W. (1965). «A measurement of excess antenna temperature at 4080 Mc/s». Astrophysical Journal. 142: 419–421. Bibcode:1965ApJ...142..419P. doi:10.1086/148307
- Peskin, Michael E.; Schroeder, Daniel V. (1995). An Introduction to Quantum Field Theory. [S.l.]: Addison-Wesley. ISBN 978-0-201-50397-5. (pede registo (ajuda))
- —— (2007). «Dark Matter and Particle Physics». Journal of the Physical Society of Japan. 76 (11). 111017 páginas. Bibcode:2007JPSJ...76k1017P. arXiv:0707.1536
 . doi:10.1143/JPSJ.76.111017
. doi:10.1143/JPSJ.76.111017
- Poisson, Eric (2004). «The Motion of Point Particles in Curved Spacetime». Living Reviews in Relativity. 7 (1). 6 páginas. Bibcode:2004LRR.....7....6P. PMC 5256043
 . PMID 28179866. arXiv:gr-qc/0306052
. PMID 28179866. arXiv:gr-qc/0306052 . doi:10.12942/lrr-2004-6
. doi:10.12942/lrr-2004-6
- —— (2004). A Relativist's Toolkit. The Mathematics of Black-Hole Mechanics. Cambridge: Cambridge University Press. Bibcode:2004rtmb.book.....P. ISBN 978-0-521-83091-1
- Polchinski, Joseph (1998a). String Theory Vol. I: An Introduction to the Bosonic String. Cambridge: Cambridge University Press. ISBN 978-0-521-63303-1
- —— (1998b). String Theory Vol. II: Superstring Theory and Beyond. Cambridge: Cambridge University Press. ISBN 978-0-521-63304-8
- Pound, R. V.; Rebka, G. A. (1959). «Gravitational Red-Shift in Nuclear Resonance». Physical Review Letters. 3 (9): 439–441. Bibcode:1959PhRvL...3..439P. doi:10.1103/PhysRevLett.3.439
- ——; Rebka, G. A. (1960). «Apparent weight of photons». Phys. Rev. Lett. 4 (7): 337–341. Bibcode:1960PhRvL...4..337P. doi:10.1103/PhysRevLett.4.337
- ——; Snider, J. L. (1964). «Effect of Gravity on Nuclear Resonance». Phys. Rev. Lett. 13 (18): 539–540. Bibcode:1964PhRvL..13..539P. doi:10.1103/PhysRevLett.13.539
- Ramond, Pierre (1990). Field Theory: A Modern Primer. [S.l.]: Addison-Wesley. ISBN 978-0-201-54611-8
- Rees, Martin (1966). «Appearance of Relativistically Expanding Radio Sources». Nature. 211 (5048): 468–470. Bibcode:1966Natur.211..468R. doi:10.1038/211468a0
- Reissner, H. (1916). «Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie». Annalen der Physik. 335 (9): 106–120. Bibcode:1916AnP...355..106R. doi:10.1002/andp.19163550905
- Remillard, Ronald A.; Lin, Dacheng; Cooper, Randall L.; Narayan, Ramesh (2006). «The Rates of Type I X-Ray Bursts from Transients Observed with RXTE: Evidence for Black Hole Event Horizons». Astrophysical Journal. 646 (1): 407–419. Bibcode:2006ApJ...646..407R. arXiv:astro-ph/0509758
 . doi:10.1086/504862
. doi:10.1086/504862
- Renn, Jürgen, ed. (2007). The Genesis of General Relativity (4 Volumes). Dordrecht: Springer. ISBN 978-1-4020-3999-7
- ——, ed. (2005). Albert Einstein—Chief Engineer of the Universe: Einstein's Life and Work in Context. Berlim: Wiley-VCH. ISBN 978-3-527-40571-8
- Reula, Oscar A. (1998). «Hyperbolic Methods for Einstein's Equations». Living Reviews in Relativity. 1 (1). 3 páginas. Bibcode:1998LRR.....1....3R. PMC 5253804
 . PMID 28191833. doi:10.12942/lrr-1998-3
. PMID 28191833. doi:10.12942/lrr-1998-3
- Rindler, Wolfgang (2001). Relativity. Special, General and Cosmological. Oxford: Oxford University Press. ISBN 978-0-19-850836-6
- —— (1991). Introduction to Special Relativity. Oxford: Clarendon Press. ISBN 978-0-19-853952-0. (pede registo (ajuda))
- Robson, Ian (1996). Active galactic nuclei. [S.l.]: John Wiley. ISBN 978-0-471-95853-6
- Roulet, E.; Mollerach, S. (1997). «Microlensing». Physics Reports. 279 (2): 67–118. Bibcode:1997PhR...279...67R. arXiv:astro-ph/9603119
 . doi:10.1016/S0370-1573(96)00020-8
. doi:10.1016/S0370-1573(96)00020-8
- Rovelli, Carlo (2000). «Notes for a brief history of quantum gravity». arXiv:gr-qc/0006061

- ——, ed. (2015). General Relativity: The most beautiful of theories (de Gruyter Studies in Mathematical Physics). Boston: Walter de Gruyter GmbH. ISBN 978-3110340426
- —— (1998). «Loop Quantum Gravity». Living Reviews in Relativity. 1 (1). 1 páginas. Bibcode:1998LRR.....1....1R. PMC 5567241
 . PMID 28937180. arXiv:gr-qc/9710008
. PMID 28937180. arXiv:gr-qc/9710008 . doi:10.12942/lrr-1998-1
. doi:10.12942/lrr-1998-1
- Schäfer, Gerhard (2004). «Gravitomagnetic Effects». General Relativity and Gravitation. 36 (10): 2223–2235. Bibcode:2004GReGr..36.2223S. arXiv:gr-qc/0407116
 . doi:10.1023/B:GERG.0000046180.97877.32
. doi:10.1023/B:GERG.0000046180.97877.32
- Schödel, R.; Ott, T.; Genzel, R.; Eckart, A.; Mouawad, N.; Alexander, T. (2003). «Stellar Dynamics in the Central Arcsecond of Our Galaxy». Astrophysical Journal. 596 (2): 1015–1034. Bibcode:2003ApJ...596.1015S. arXiv:astro-ph/0306214
 . doi:10.1086/378122
. doi:10.1086/378122
- Schutz, Bernard F. (1985). A first course in general relativity. Cambridge: Cambridge University Press. ISBN 978-0-521-27703-7
- —— (2001). «Gravitational radiation». In: Murdin, Paul. Encyclopedia of Astronomy and Astrophysics. Grove's Dictionaries. ISBN 978-1-56159-268-5
- —— (2003). Gravity from the ground up. Cambridge: Cambridge University Press. ISBN 978-0-521-45506-0
- Schwarz, John H. (2007). «String Theory: Progress and Problems». Progress of Theoretical Physics Supplement. 170: 214–226. Bibcode:2007PThPS.170..214S. arXiv:hep-th/0702219
 . doi:10.1143/PTPS.170.214
. doi:10.1143/PTPS.170.214
- Schwarzschild, Karl (1916a). «Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie». Sitzungsber. Preuss. Akad. D. Wiss.: 189–196. Bibcode:1916SPAW.......189S
- —— (1916b). «Über das Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie». Sitzungsber. Preuss. Akad. D. Wiss.: 424–434. Bibcode:1916skpa.conf..424S
- Seidel, Edward (1998). Narlikar, J. V.; Dadhich, N., eds. Numerical Relativity: Towards Simulations of 3D Black Hole Coalescence. «Gravitation and Relativity: At the turn of the millennium (Proceedings of the GR-15 Conference, held at IUCAA, Pune, India, December 16–21, 1997)». IUCAA. 6088 páginas. Bibcode:1998gr.qc.....6088S. ISBN 978-81-900378-3-9. arXiv:gr-qc/9806088

- Seljak, Uros̆; Zaldarriaga, Matias (1997). «Signature of Gravity Waves in the Polarization of the Microwave Background». Phys. Rev. Lett. 78 (11): 2054–2057. Bibcode:1997PhRvL..78.2054S. arXiv:astro-ph/9609169
 . doi:10.1103/PhysRevLett.78.2054
. doi:10.1103/PhysRevLett.78.2054
- Shapiro, S. S.; Davis, J. L.; Lebach, D. E.; Gregory, J. S. (2004). «Measurement of the solar gravitational deflection of radio waves using geodetic very-long-baseline interferometry data, 1979–1999». Phys. Rev. Lett. 92 (12). 121101 páginas. Bibcode:2004PhRvL..92l1101S. PMID 15089661. doi:10.1103/PhysRevLett.92.121101
- Shapiro, Irwin I. (1964). «Fourth test of general relativity». Phys. Rev. Lett. 13 (26): 789–791. Bibcode:1964PhRvL..13..789S. doi:10.1103/PhysRevLett.13.789
- ——; Pettengill, Gordon; Ash, Michael; Stone, Melvin; Smith, William; Ingalls, Richard; Brockelman, Richard (1968). «Fourth test of general relativity: preliminary results». Phys. Rev. Lett. 20 (22): 1265–1269. Bibcode:1968PhRvL..20.1265S
- Singh, Simon (2004). Big Bang: The Origin of the Universe. [S.l.]: Fourth Estate. Bibcode:2004biba.book.....S. ISBN 978-0-00-715251-3
- Sorkin, Rafael D. (2005). «Causal Sets: Discrete Gravity». In: Gomberoff, Andres; Marolf, Donald. Lectures on Quantum Gravity. [S.l.]: Springer. p. 9009. ISBN 978-0-387-23995-8. arXiv:gr-qc/0309009

- —— (1997). «Forks in the Road, on the Way to Quantum Gravity». Int. J. Theor. Phys. 36 (12): 2759–2781. Bibcode:1997IJTP...36.2759S. arXiv:gr-qc/9706002
 . doi:10.1007/BF02435709
. doi:10.1007/BF02435709
- Spergel, D. N.; Verde, L.; Peiris, H. V.; Komatsu, E.; Nolta, M. R.; Bennett, C. L.; Halpern, M.; Hinshaw, G.; Jarosik, N. (2003). «First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters». Astrophys. J. Suppl. Ser. 148 (1): 175–194. Bibcode:2003ApJS..148..175S. arXiv:astro-ph/0302209
 . doi:10.1086/377226
. doi:10.1086/377226
- ——; Bean, R.; Doré, O.; Nolta, M. R.; Bennett, C. L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.; Komatsu, E. (2007). «Wilkinson Microwave Anisotropy Probe (WMAP) Three Year Results: Implications for Cosmology». Astrophysical Journal Supplement. 170 (2): 377–408. Bibcode:2007ApJS..170..377S. arXiv:astro-ph/0603449
 . doi:10.1086/513700
. doi:10.1086/513700
- Springel, Volker; White, Simon D. M.; Jenkins, Adrian; Frenk, Carlos S.; Yoshida, Naoki; Gao, Liang; Navarro, Julio; Thacker, Robert; Croton, Darren (2005). «Simulations of the formation, evolution and clustering of galaxies and quasars». Nature. 435 (7042): 629–636. Bibcode:2005Natur.435..629S. PMID 15931216. arXiv:astro-ph/0504097
 . doi:10.1038/nature03597
. doi:10.1038/nature03597
- Stairs, Ingrid H. (2003). «Testing General Relativity with Pulsar Timing». Living Reviews in Relativity. 6 (1). 5 páginas. Bibcode:2003LRR.....6....5S. PMC 5253800
 . PMID 28163640. arXiv:astro-ph/0307536
. PMID 28163640. arXiv:astro-ph/0307536 . doi:10.12942/lrr-2003-5
. doi:10.12942/lrr-2003-5
- Stephani, H.; Kramer, D.; MacCallum, M.; Hoenselaers, C.; Herlt, E. (2003). Exact Solutions of Einstein's Field Equations 2 ed. Cambridge: Cambridge University Press. ISBN 978-0-521-46136-8
- Synge, J. L. (1972). Relativity: The Special Theory. [S.l.]: North-Holland Publishing Company. ISBN 978-0-7204-0064-9
- Szabados, László B. (2004). «Quasi-Local Energy-Momentum and Angular Momentum in GR». Living Reviews in Relativity. 7 (1). 4 páginas. Bibcode:2004LRR.....7....4S. PMC 5255888
 . PMID 28179865. doi:10.12942/lrr-2004-4
. PMID 28179865. doi:10.12942/lrr-2004-4
- Taylor, Joseph H. (1994). «Binary pulsars and relativistic gravity». Rev. Mod. Phys. 66 (3): 711–719. Bibcode:1994RvMP...66..711T. doi:10.1103/RevModPhys.66.711
- Thiemann, Thomas (2007). «Approaches to Fundamental Physics: Loop Quantum Gravity: An Inside View». Lecture Notes in Physics. 721: 185–263. Bibcode:2007LNP...721..185T. ISBN 978-3-540-71115-5. arXiv:hep-th/0608210
 . doi:10.1007/978-3-540-71117-9_10
. doi:10.1007/978-3-540-71117-9_10
- —— (2003). «Lectures on Loop Quantum Gravity». Lecture Notes in Physics. 631: 41–135. Bibcode:2003LNP...631...41T. ISBN 978-3-540-40810-9. arXiv:gr-qc/0210094
 . doi:10.1007/978-3-540-45230-0_3
. doi:10.1007/978-3-540-45230-0_3
- 't Hooft, Gerard; Veltman, Martinus (1974). «One Loop Divergencies in the Theory of Gravitation». Ann. Inst. Poincare. 20 (1). 69 páginas. Bibcode:1974AIHPA..20...69T
- Thorne, Kip S. (1972). «Nonspherical Gravitational Collapse—A Short Review». In: Klauder, J. Magic without Magic. [S.l.]: W. H. Freeman. p. 231–258
- —— (1994). Black Holes and Time Warps: Einstein's Outrageous Legacy. [S.l.]: W W Norton & Company. ISBN 978-0-393-31276-8
- —— (1995). «Gravitational radiation». Particle and Nuclear Astrophysics and Cosmology in the Next Millenium. 160 páginas. Bibcode:1995pnac.conf..160T. ISBN 978-0-521-36853-7. arXiv:gr-qc/9506086

- Townsend, Paul K. (1997). «Black Holes (Lecture notes)». arXiv:gr-qc/9707012

- —— (2003). The future of theoretical physics and cosmology: celebrating Stephen Hawking's 60th birthday. Cambridg: Cambridge University Press. ISBN 0-521-82081-2
- —— (1996). «Four Lectures on M-Theory». High Energy Physics and Cosmology. 13. 385 páginas. Bibcode:1997hepcbconf..385T. arXiv:hep-th/9612121

- Traschen, Jenny (2000). Bytsenko, A.; Williams, F., eds. «An Introduction to Black Hole Evaporation». World Scientific. Mathematical Methods of Physics (Proceedings of the 1999 Londrina Winter School). 180 páginas. Bibcode:2000mmp..conf..180T. arXiv:gr-qc/0010055

- Trautman, Andrzej (2006). «Einstein–Cartan theory». In: Françoise, J.-P.; Naber, G. L.; Tsou, S. T. Encyclopedia of Mathematical Physics, Vol. 2. [S.l.]: Elsevier. p. 189–195. Bibcode:2006gr.qc.....6062T. arXiv:gr-qc/0606062

- Unruh, W. G. (1976). «Notes on Black Hole Evaporation». Phys. Rev. D. 14 (4): 870–892. Bibcode:1976PhRvD..14..870U. doi:10.1103/PhysRevD.14.870
- Valtonen, M. J.; Lehto, H. J.; Nilsson, K.; Heidt, J.; Takalo, L. O.; Sillanpää, A.; Villforth, C.; Kidger, M.; Poyner, G. (2008). «A massive binary black-hole system in OJ 287 and a test of general relativity». Nature. 452 (7189): 851–853. Bibcode:2008Natur.452..851V. PMID 18421348. arXiv:0809.1280
 . doi:10.1038/nature06896
. doi:10.1038/nature06896
- Veltman, Martinus (1975). Balian, Roger; Zinn-Justin, Jean, eds. «Methods in Field Theory - Les Houches Summer School in Theoretical Physics». North Holland. 77
- Wald, Robert M. (1975). «On Particle Creation by Black Holes». Commun. Math. Phys. 45 (3): 9–34. Bibcode:1975CMaPh..45....9W. doi:10.1007/BF01609863
- —— (1984). General Relativity. Chicago: University of Chicago Press. ISBN 978-0-226-87033-5
- —— (1994). Quantum field theory in curved spacetime and black hole thermodynamics. Chicago: University of Chicago Press. ISBN 978-0-226-87027-4
- —— (2001). «The Thermodynamics of Black Holes». Living Reviews in Relativity. 4 (1). 6 páginas. Bibcode:2001LRR.....4....6W. PMC 5253844
 . PMID 28163633. arXiv:gr-qc/9912119
. PMID 28163633. arXiv:gr-qc/9912119 . doi:10.12942/lrr-2001-6
. doi:10.12942/lrr-2001-6
- Walsh, D.; Carswell, R. F.; Weymann, R. J. (1979). «0957 + 561 A, B: twin quasistellar objects or gravitational lens?». Nature. 279 (5712): 381–4. Bibcode:1979Natur.279..381W. PMID 16068158. doi:10.1038/279381a0
- Wambsganss, Joachim (1998). «Gravitational Lensing in Astronomy». Living Reviews in Relativity. 1 (1). 12 páginas. Bibcode:1998LRR.....1...12W. PMC 5567250
 . PMID 28937183. arXiv:astro-ph/9812021
. PMID 28937183. arXiv:astro-ph/9812021 . doi:10.12942/lrr-1998-12
. doi:10.12942/lrr-1998-12
- Weinberg, Steven (1972). Gravitation and Cosmology. [S.l.]: John Wiley. ISBN 978-0-471-92567-5
- —— (1975). The Quantum Theory of Fields I: Foundations. Cambridge: Cambridge University Press. ISBN 978-0-521-55001-7
- —— (1996). The Quantum Theory of Fields II: Modern Applications. Cambridge: Cambridge University Press. ISBN 978-0-521-55002-4. (pede registo (ajuda))
- —— (2000). The Quantum Theory of Fields III: Supersymmetry. Cambridge: Cambridge University Press. ISBN 978-0-521-66000-6. (pede registo (ajuda))
- Weisberg, Joel M.; Taylor, Joseph H. (2003). Proceedings of "Radio Pulsars," Chania, Crete, August, 2002. «The Relativistic Binary Pulsar B1913+16"» ASP Conference Series ed. arXiv:astro-ph/0211217v1

- Weiss, Achim (2006). «Elements of the past: Big Bang Nucleosynthesis and observation». Einstein Online. Max Planck Institute for Gravitational Physics. Cópia arquivada em 8 de fevereiro de 2007
- Wheeler, John A. (1990). A Journey Into Gravity and Spacetime. Col: Scientific American Library. São Francisco, CA: W. H. Freeman. ISBN 978-0-7167-6034-4
- Will, Clifford M. (1993). Theory and experiment in gravitational physics. [S.l.]: Cambridge University Press. ISBN 0-521-43973-6
- —— (2006). «The Confrontation between General Relativity and Experiment». Living Rev. Relativity. 9 (1). 3 páginas. Bibcode:2006LRR.....9....3W. PMC 5256066
 . PMID 28179873. doi:10.12942/lrr-2006-3
. PMID 28179873. doi:10.12942/lrr-2006-3
- Zwiebach, Barton (2004). A First Course in String Theory. Cambridge: Cambridge University Press. ISBN 978-0-521-83143-7
Leitura adicional[editar código-fonte]
- Callahan, James J. (2000). The Geometry of Spacetime: an Introduction to Special and General Relativity. Nova Iorque: Springer. ISBN 978-0-387-98641-8
- Carroll, Sean M. (2004). Spacetime and Geometry: An Introduction to General Relativity. São Francisco: Addison-Wesley. ISBN 978-0-8053-8732-2
- Chandrasekhar, Subrahmanyan (1983). The Mathematical Theory of Black Holes. [S.l.]: Oxford University Press. ISBN 978-0-226-10087-6
- Cheng, Ta-Pei (2005). Relativity, Gravitation and Cosmology: a Basic Introduction. Oxford e Nova Iorque: Oxford University Press. ISBN 978-0-19-852957-6
- d'Inverno, Ray (1992). Introducing Einstein's Relativity. Oxford: Oxford University Press. ISBN 978-0-19-859686-8. (pede subscrição (ajuda))
- Einstein, Albert (1916). Relativity: The Special and the General Theory. Berlim: [s.n.] ISBN 978-3-528-06059-6
- Geroch, Robert (1981). General Relativity from A to B. Chicago: University of Chicago Press. ISBN 978-0-226-28864-2
- Grøn, Øyvind; Hervik, Sigbjørn (2007). Einstein's General Theory of Relativity. Nova Iorque: Springer. ISBN 978-0-387-69199-2
- Hartle, James B. (2003). Gravity: an Introduction to Einstein's General Relativity. São Francisco: Addison-Wesley. ISBN 978-0-8053-8662-2
- Hawking, Stephen; Ellis, George (1975). The Large Scale Structure of Space-time. [S.l.]: Cambridge University Press. ISBN 978-0521099066
- Hughston, Lane P.; Tod, K. P. (1991). Introduction to General Relativity. Cambridge: Cambridge University Press. ISBN 978-0-521-33943-8
- Landau, Lev; Lifshitz, Evgeny (1980). The Classical Theory of Fields (4th ed.). Londres: Butterworth-Heinemann. ISBN 978-0-7506-2768-9
- Lieber, Lillian (2008). The Einstein Theory of Relativity: A Trip to the Fourth Dimension. Filadélfia, PA: Paul Dry Books, Inc. ISBN 978-1-58988-044-3
- Ludyk, Günter (2013). Einstein in Matrix Form 1 ed. Berlim: Springer. ISBN 978-3-642-35797-8
- Moore, Thomas A. (2012). A General Relativity Workbook. [S.l.]: University Science Books. ISBN 978-1-891389-82-5
- Misner, Charles W.; Thorne, Kip; Wheeler, John (1973). Gravitation. [S.l.]: W. H. Freeman. ISBN 978-0-7167-0344-0
- Poisson, Eric (2007). A Relativist's Toolkit: The Mathematics of Black-Hole Mechanics. [S.l.]: Cambridge University Press. ISBN 978-0521537803
- Schutz, B. F. (2008). A First Course in General Relativity 2 ed. Cambridge: Cambridge University Press. ISBN 978-0-521-88705-2
- Stephani, Hans (1990). General Relativity: An Introduction to the Theory of the Gravitational Field. Cambridge: Cambridge University Press. ISBN 978-0-521-37941-0
- Taylor, Edwin F.; Wheeler, John Archibald (2000). Exploring Black Holes: Introduction to General Relativity. [S.l.]: Addison Wesley. ISBN 978-0-201-38423-9
- Thorne, Kip (1994). Black Holes and Time Warps: Einstein's Outrageous Legacy. Nova Iorque: W. W. Norton. ISBN 0393035050
- Wald, Robert (1992). Space, Time, and Gravity: the Theory of the Big Bang and Black Holes. Chicago: University of Chicago Press. ISBN 978-0-226-87029-8
- Wheeler, John; Ford, Kenneth (1998). Geons, Black Holes, & Quantum Foam: a life in physics. Nova Iorque: W. W. Norton. ISBN 978-0-393-31991-0
- Wald, Robert (1984). General Relativity. Chicago: University of Chicago Press. ISBN 978-0-226-87033-5
- Weinberg, Steven (1972). Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. Nova Iorque: Wiley. ISBN 0471925675
- Will, Clifford; Poisson, Eric (2004). Gravity: Newtonian, Post-Newtonian, Relativistic. [S.l.]: Cambridge University Press. ISBN 978-1107032866
Ligações externas[editar | editar código-fonte]
- «Relatividade». no FisicaNET
- «Relatividade Geral». no Ciência Hoje
- «Geometria e experiência (1921)». no SciELO
- «Legado da relatividade». no Scientific American Brasil



















