Excentricidade orbital

Elíptica (excentricidade = 0.7)
Parabólica (excentricidade = 1)
Hiperbólica (excentricidade = 1.3)

0.0 · 0.2 · 0.4 · 0.6 · 0.8
| Parte de uma série sobre |
| Astrodinâmica |
|---|
 |
|
Influências gravitacionais |
|
Engenharia de pré-voo |
|
Medidas de eficiência |
Em astrodinâmica, a excentricidade orbital de um objeto astronômico é um parâmetro adimensional que determina o quanto sua órbita em torno de outro corpo se desvia de um círculo perfeito. Um valor de 0 é uma órbita circular, valores entre 0 e 1 formam uma órbita elíptica, 1 é uma órbita de escape parabólica e maior que 1 é uma hipérbole. O termo deriva seu nome dos parâmetros das seções cônicas, já que toda órbita kepleriana é uma seção cônica. É normalmente usado para o isolado problema dos dois corpos, mas existem extensões para objetos que seguem uma roseta orbitando pela galáxia.
Definição[editar | editar código-fonte]
Em um problema dos dois corpos em que a força seja função do inverso do quadrado da distância, cada órbita é uma órbita kepleriana. A excentricidade desta órbita é um número não-negativo que define sua forma.
A excentricidade pode assumir os seguintes valores:
- Órbita circular: e = 0
- Órbita elíptica: 0 < e < 1 (veja elipse)
- Trajetória parabólica: e = 1 (veja parábola)
- Trajetória hiperbólica: e > 1 (veja hipérbole)
A excentricidade e é dada por
onde E é a energia orbital total, L é o momento angular, mred é a massa reduzida e α o coeficiente da força central da lei do inverso do quadrado, como gravidade ou eletrostática na física clássica:
-
- (α é negativo para uma força atrativa, positivo para uma força repulsiva; veja também problema Kepler)
ou no caso de uma força gravitacional:
onde ε é a energia orbital específica (energia total dividida pela massa reduzida), μ o parâmetro gravitacional padrão com base na massa total e h o momento angular relativo específico (momento angular dividido pela massa reduzida).
Para valores de e de 0 a 1, a forma da órbita é uma elipse cada vez mais alongada (ou mais plana); para valores de e de 1 a infinito, a órbita é um ramo de hipérbole que faz uma volta total de 2 arccsc e, diminuindo de 180 para 0 graus. O caso limite entre uma elipse e uma hipérbole, quando e é igual a 1, é a parábola.
As trajetórias radiais são classificadas como elípticas, parabólicas ou hiperbólicas com base na energia da órbita, não na excentricidade. As órbitas radiais têm momento angular zero e, portanto, excentricidade igual a um. Mantendo a energia constante e reduzindo o momento angular, as órbitas elíptica, parabólica e hiperbólica tendem, cada uma, ao tipo correspondente de trajetória radial, enquanto e tende a 1 (ou no caso parabólico, permanece 1).
Para uma força repulsiva, apenas a trajetória hiperbólica, incluindo a versão radial, é aplicável.
Para órbitas elípticas, uma prova simples mostra que arcsin() produz o ângulo de projeção de um círculo perfeito para uma elipse de excentricidade e. Por exemplo, para visualizar a excentricidade do planeta Mercúrio (e = 0.2056), deve-se simplesmente calcular o seno inverso para encontrar o ângulo de projeção de 11.86 graus. Em seguida, incline qualquer objeto circular (como uma caneca de café vista de cima) nesse ângulo e a elipse aparente projetada em seu olho terá a mesma excentricidade.
Etimologia[editar | editar código-fonte]
A palavra "excentricidade" vem do latim medieval eccentricus, derivado do grego antigo ἔκκεντρος ekkentros "fora do centro", de ἐκ- ek-, "fora de" + κέντρον kentron "centro". "Excêntrico" apareceu pela primeira vez na Inglaterra em 1551, com a definição "...um círculo no qual a Terra, Sol, etc, se desvia de seu centro". Cinco anos depois, em 1556, uma forma adjetiva da palavra se desenvolveu.
Cálculo[editar | editar código-fonte]
A excentricidade de uma órbita pode ser calculada a partir dos vetores de estado orbital como a magnitude do vetor de excentricidade:
onde:
- e é o vetor de excentricidade ("Hamilton's vector").
Para órbitas elípticas, também pode ser calculado a partir do periapsis e apoapsis, uma vez que and onde a é o comprimento do semieixo maior, a distância média geométrica e média temporal.
onde:
- ra é o raio na apoapsis (também conhecido como "apofoco", "afélio", "apogeu", ou seja, a distância mais distante da órbita ao centro de massa do sistema, que é um foco da elipse).
- rp é o raio no periapsis (também conhecido como "perifocus" etc., a distância mais próxima).
A excentricidade de uma órbita elíptica também pode ser usada para obter a razão entre o raio do periapsis e o raio da apoapsis:
Para a Terra, excentricidade orbital e ≈ 0.01671, apoapsis é afélio, e periapsis é periélio em relação ao Sol.
Para o caminho da órbita anual da Terra, a proporção do raio mais longo (ra) / raio mais curto (rp) é
Exemplos[editar | editar código-fonte]
| Objeto | Excentricidade |
|---|---|
| Tritão | 0.00002 |
| Vênus | 0.0068 |
| Netuno | 0.0086 |
| Terra | 0.0167 |
| Titã | 0.0288 |
| Urano | 0.0472 |
| Júpiter | 0.0484 |
| Saturno | 0.0541 |
| Lua | 0.0549 |
| 1 Ceres | 0.0758 |
| 4 Vesta | 0.0887 |
| Marte | 0.0934 |
| 10 Hígia | 0.1146 |
| Makemake | 0.1559 |
| Haumea | 0.1887 |
| Mercúrio | 0.2056 |
| 2 Palas | 0.2313 |
| Plutão | 0.2488 |
| 3 Juno | 0.2555 |
| 324 Bamberga | 0.3400 |
| Éris | 0.4407 |
| Nereida | 0.7507 |
| Sedna | 0.8549 |
| Cometa Halley | 0.9671 |
| Cometa Hale-Bopp | 0.9951 |
| Cometa Ikeya-Seki | 0.9999 |
| C/1980 E1 (Bowell) | 1.057 |
| ʻOumuamua | 1.20[a] |
| 2I/Borisov | 3.5[b] |
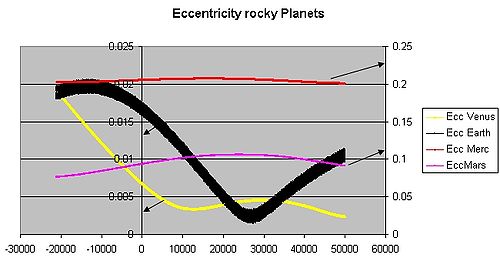
A excentricidade da órbita da Terra é atualmente cerca de 0.0167; a órbita da Terra é quase circular. Vênus e Netuno têm excentricidades ainda mais baixas. Ao longo de centenas de milhares de anos, a excentricidade da órbita da Terra varia de quase 0.0034 a quase 0.058 como resultado das atrações gravitacionais entre os planetas (ver gráfico).[1]
A tabela lista os valores para todos os planetas e planetas anões e asteroides, cometas e satélites naturais selecionados. Mercúrio tem a maior excentricidade orbital de qualquer planeta do Sistema Solar (e = 0.2056). Essa excentricidade é suficiente para Mercúrio receber duas vezes mais irradiação solar no periélio em comparação com o afélio. Antes de seu rebaixamento do status de planeta em 2006, Plutão era considerado o planeta com a órbita mais excêntrica (e = 0.248). Outros objetos transnetunianos têm excentricidade significativa, notavelmente o planeta anão Éris (0.44). Ainda mais longe, Sedna, tem uma excentricidade extremamente alta de 0.855 devido ao seu afélio estimado de 937 unidades astronômicas (UA) e periélio de cerca de 76 UA.
A maioria dos asteroides do Sistema Solar tem excentricidades orbitais entre 0 e 0.35 com um valor médio de 0.17.[2] Suas excentricidades comparativamente altas são provavelmente devido à influência de Júpiter e a colisões anteriores.
O valor da Lua é 0.0549, a mais excêntrica dos grandes satélites naturais do Sistema Solar. As quatro luas galileanas têm excentricidade < 0.01. A maior lua de Netuno, Tritão, tem uma excentricidade de 1.6×10−5 (0.000016),[3] a menor excentricidade de qualquer lua conhecida no Sistema Solar; sua órbita é o mais próximo de um círculo perfeito que pode ser medido atualmente. No entanto, luas menores, particularmente satélites irregulares, podem ter excentricidade significativa, como a terceira maior lua de Netuno, Nereida (0.75).
Os cometas têm valores de excentricidade muito diferentes. Os cometas periódicos têm excentricidades principalmente entre 0.2 e 0.7,[4] mas alguns deles têm órbitas elípticas altamente excêntricas com excentricidades logo abaixo de 1, por exemplo, o Cometa Halley tem um valor de 0.967. Cometas não-periódicos seguem órbitas quase parabólicas e, portanto, têm excentricidades ainda mais próximas de 1. Os exemplos incluem o Cometa Hale-Bopp com um valor de 0.995[5] e o Cometa McNaught com um valor de 1.000019.[6] Como o valor do Cometa Hale-Bopp é menor que 1, sua órbita é elíptica e ele retornará.[5] O Cometa McNaught tem uma órbita hiperbólica enquanto está sob a influência dos planetas,[6] mas ainda está ligado ao Sol com um período orbital de cerca de 105 anos.[7] O Cometa C/1980 E1 (Bowell) tem a maior excentricidade de qualquer cometa hiperbólico conhecido de origem solar com uma excentricidade de 1.057,[8] e deixará o Sistema Solar eventualmente.
ʻOumuamua é o primeiro objeto interestelar encontrado passando pelo Sistema Solar. Sua excentricidade orbital de 1.20 indica que ʻOumuamua nunca foi gravitacionalmente ligado ao nosso Sol. Foi descoberto a 0.2 UA 30.000.000 km da Terra e tem cerca de 200 metros de diâmetro. Tem uma velocidade interestelar (velocidade no infinito) de 26.33 km/s.
Excentricidade média[editar | editar código-fonte]
A excentricidade média de um objeto é a excentricidade média como resultado de perturbações durante um determinado período de tempo. Netuno atualmente tem uma excentricidade instantânea (época atual) de 0.0113,[9] mas de 1800 a 2050 tem uma excentricidade média de 0.00859.[10]
Efeito climático[editar | editar código-fonte]
A mecânica orbital requer que a duração das estações seja proporcional à área da órbita da Terra varrida entre os solstícios e equinócios, então, quando a excentricidade orbital é extrema, as estações que ocorrem no outro lado da órbita (afélio) podem ser substancialmente mais longa em duração. Hoje, o outono e o inverno do hemisfério norte ocorrem na aproximação mais próxima (periélio), quando a Terra está se movendo em sua velocidade máxima, enquanto o oposto ocorre no hemisfério sul. Como resultado, no hemisfério norte, o outono e o inverno são ligeiramente mais curtos do que a primavera e o verão mas, em termos globais, isso é equilibrado com eles sendo mais longos abaixo do equador. Em 2006, o verão do hemisfério norte foi 4.66 dias a mais que o inverno, e a primavera foi 2.9 dias a mais que o outono devido aos ciclos de variação orbital.[11][12]
A precessão apsidal também muda lentamente o lugar na órbita da Terra onde ocorrem os solstícios e equinócios. Observe que esta é uma mudança lenta na órbita da Terra, não no eixo de rotação, que é referido como precessão axial (veja Precessão § Astronomia). Nos próximos 10.000 anos, os invernos do hemisfério norte se tornarão gradualmente mais longos e os verões mais curtos. No entanto, qualquer efeito de resfriamento em um hemisfério é equilibrado pelo aquecimento no outro, e qualquer mudança geral será contrabalançada pelo fato de que a excentricidade da órbita da Terra será reduzida quase pela metade.[13] Isso reduzirá o raio orbital médio e aumentará as temperaturas em ambos os hemisférios para mais perto do pico interglacial médio.
Exoplanetas[editar | editar código-fonte]
Dos muitos exoplanetas descobertos, a maioria tem uma excentricidade orbital mais alta do que os planetas em nosso Sistema Solar. Os exoplanetas encontrados com baixa excentricidade orbital (órbitas quase circulares) estão muito próximos de sua estrela e são fixados pela força de maré da estrela. Todos os oito planetas do Sistema Solar têm órbitas quase circulares. Os exoplanetas descobertos mostram que o Sistema Solar, com sua excepcionalmente baixa excentricidade, é raro e único.[14] Uma teoria atribui essa baixa excentricidade ao alto número de planetas no Sistema Solar; outro sugere que surgiu por causa de seus cinturões de asteroides exclusivos. Alguns outros sistemas multiplanetários foram encontrados, mas nenhum se assemelha ao Sistema Solar. O Sistema Solar possui sistemas planetesimais únicos, o que levou os planetas a terem órbitas quase circulares. Os sistemas planetesimais solares incluem o cinturão de asteroides, família Hilda, cinturão de Kuiper, nuvem de Hills e a nuvem de Oort. Os sistemas de exoplanetas descobertos não possuem sistemas planetesimais ou possuem um sistema muito grande. A baixa excentricidade é necessária para a habitabilidade, especialmente na vida avançada.[15] Os sistemas de planetas de alta multiplicidade têm muito mais probabilidade de ter exoplanetas habitáveis.[16][17] A hipótese da grande aderência do Sistema Solar também ajuda a entender suas órbitas quase circulares e outras características únicas.[18][19][20][21][22][23][24][25]
Notas
Referências
- ↑ A. Berger; M.F. Loutre (1991). «Graph of the eccentricity of the Earth's orbit». Illinois State Museum (Insolation values for the climate of the last 10 million years). Arquivado do original em 6 de janeiro de 2018 Verifique o valor de
|name-list-format=amp(ajuda) - ↑ Asteroids Arquivado em 4 março 2007 no Wayback Machine
- ↑ David R. Williams (22 de janeiro de 2008). «Neptunian Satellite Fact Sheet». NASA
- ↑ Lewis, John (2 de dezembro de 2012). Physics and Chemistry of the Solar System. [S.l.]: Academic Press. ISBN 9780323145848
- ↑ a b «JPL Small-Body Database Browser: C/1995 O1 (Hale-Bopp)» (2007-10-22 last obs). Consultado em 5 de dezembro de 2008
- ↑ a b «JPL Small-Body Database Browser: C/2006 P1 (McNaught)» (2007-07-11 last obs). Consultado em 17 de dezembro de 2009
- ↑ «Comet C/2006 P1 (McNaught) – facts and figures». Perth Observatory in Australia. 22 de janeiro de 2007. Arquivado do original em 18 de fevereiro de 2011
- ↑ «JPL Small-Body Database Browser: C/1980 E1 (Bowell)» (1986-12-02 last obs). Consultado em 22 de março de 2010
- ↑ Williams, David R. (29 de novembro de 2007). «Neptune Fact Sheet». NASA
- ↑ «Keplerian elements for 1800 A.D. to 2050 A.D.». JPL Solar System Dynamics. Consultado em 17 de dezembro de 2009
- ↑ Data from United States Naval Observatory
- ↑ Berger A.; Loutre M.F.; Mélice J.L. (2006). «Equatorial insolation: from precession harmonics to eccentricity frequencies» (PDF). Clim. Past Discuss. 2 (4): 519–533. doi:10.5194/cpd-2-519-2006

- ↑ Arizona U., Long Term Climate
- ↑ exoplanets.org, ORBITAL ECCENTRICITES, by G.Marcy, P.Butler, D.Fischer, S.Vogt, 20 Sept 2003
- ↑ Ward, Peter; Brownlee, Donald (2000). Rare Earth: Why Complex Life is Uncommon in the Universe. [S.l.]: Springer. pp. 122–123. ISBN 0-387-98701-0
- ↑ Limbach, MA; Turner, EL (2015). «Exoplanet orbital eccentricity: multiplicity relation and the Solar System». Proc Natl Acad Sci U S A. 112 (1): 20–4. Bibcode:2015PNAS..112...20L. PMC 4291657
 . PMID 25512527. arXiv:1404.2552
. PMID 25512527. arXiv:1404.2552 . doi:10.1073/pnas.1406545111
. doi:10.1073/pnas.1406545111
- ↑ Steward Observatory, University of Arizona, Tucson, Planetesimals in Debris Disks, by Andrew N. Youdin and George H. Rieke, 2015
- ↑ Zubritsky, Elizabeth. «Jupiter's Youthful Travels Redefined Solar System». NASA. Consultado em 4 de novembro de 2015
- ↑ Sanders, Ray. «How Did Jupiter Shape Our Solar System?». Universe Today. Consultado em 4 de novembro de 2015
- ↑ Choi, Charles Q. «Jupiter's 'Smashing' Migration May Explain Our Oddball Solar System». Space.com. Consultado em 4 de novembro de 2015
- ↑ Davidsson, Dr. Björn J. R. «Mysteries of the asteroid belt». The History of the Solar System. Consultado em 7 de novembro de 2015
- ↑ Raymond, Sean. «The Grand Tack». PlanetPlanet. Consultado em 7 de novembro de 2015
- ↑ O'Brien, David P.; Walsh, Kevin J.; Morbidelli, Alessandro; Raymond, Sean N.; Mandell, Avi M. (2014). «Water delivery and giant impacts in the 'Grand Tack' scenario». Icarus. 239: 74–84. Bibcode:2014Icar..239...74O. arXiv:1407.3290
 . doi:10.1016/j.icarus.2014.05.009
. doi:10.1016/j.icarus.2014.05.009
- ↑ Loeb, Abraham; Batista, Rafael; Sloan, David (agosto de 2016). «Relative Likelihood for Life as a Function of Cosmic Time». Journal of Cosmology and Astroparticle Physics. 2016 (8). 040 páginas. Bibcode:2016JCAP...08..040L. arXiv:1606.08448
 . doi:10.1088/1475-7516/2016/08/040
. doi:10.1088/1475-7516/2016/08/040
- ↑ «Is Earthly Life Premature from a Cosmic Perspective?». Harvard-Smithsonian Center for Astrophysics. 1 de agosto de 2016
Leitura adicional[editar | editar código-fonte]
- Prussing, John E.; Conway, Bruce A. (1993). Orbital Mechanics. New York: Oxford University Press. ISBN 0-19-507834-9. (pede registo (ajuda))
Ligações externas[editar | editar código-fonte]
- World of Physics: Eccentricity
- The NOAA page on Climate Forcing Data includes (calculated) data from Berger (1978), Berger and Loutre (1991)[ligação inativa]. Laskar et al. (2004) on Earth orbital variations, Includes eccentricity over the last 50 million years and for the coming 20 million years.
- The orbital simulations by Varadi, Ghil and Runnegar (2003) provides series for Earth orbital eccentricity and orbital inclination.
- Kepler's Second law's simulation












