Buraco negro

Buraco negro é uma região do espaço-tempo em que o campo gravitacional é tão intenso que nada — nenhuma partícula ou radiação eletromagnética como a luz — pode escapar.[6] A teoria da relatividade geral prevê que uma massa suficientemente compacta pode deformar o espaço-tempo para formar um buraco negro.[7][8] O limite da região da qual não é possível escapar é chamado de horizonte de eventos. Embora o horizonte de eventos tenha um efeito enorme sobre o destino e as circunstâncias de um objeto que o atravessa, não tem nenhuma característica local detectável.[9] De muitas maneiras, um buraco negro age como um corpo negro ideal, pois não reflete luz.[10][11] Além disso, a teoria quântica de campos no espaço-tempo curvo prevê que os horizontes de eventos emitem radiação Hawking, com o mesmo espectro que um corpo negro de temperatura inversamente proporcional à sua massa. Essa temperatura é da ordem dos bilionésimos de um kelvin para buracos negros de massa estelar, o que a torna praticamente impossível de observar.
Objetos cujos campos gravitacionais são fortes demais para a luz escapar foram considerados pela primeira vez no século XVIII por John Michell e Pierre-Simon Laplace.[12] A primeira solução moderna da relatividade geral que caracterizaria um buraco negro foi encontrada por Karl Schwarzschild em 1916, embora sua interpretação como uma região do espaço da qual nada possa escapar tenha sido publicada pela primeira vez por David Finkelstein em 1958. Os buracos negros eram há muito considerados uma curiosidade matemática; foi na década de 1960 que o trabalho teórico mostrou que eram uma previsão genérica da relatividade geral. A descoberta de estrelas de nêutrons por Jocelyn Bell Burnell em 1967 despertou o interesse em objetos compactos em colapso gravitacional como uma possível realidade astrofísica.
Espera-se a formação de buracos negros de massa estelar quando estrelas muito massivas colapsam no final de seu ciclo de vida. Um buraco negro pode se formar também a partir da condensação de nuvens de gás.[13] Uma descoberta de novembro de 2023 é consistente com essa hipótese.[14] Após a formação de um buraco negro, ele pode continuar a crescer absorvendo a massa do ambiente. Ao absorver outras estrelas e se fundir com outros buracos negros, buracos negros supermassivos de milhões de massas solares (M☉) podem se formar. Há consenso de que existem buracos negros supermassivos no centro da maioria das galáxias. A presença de um buraco negro pode ser inferida por meio da interação com outra matéria e com radiação eletromagnética, como a luz visível. A matéria que cai em um buraco negro pode formar um disco de acreção externa aquecido por fricção, formando alguns dos objetos mais brilhantes do universo. Se houver outras estrelas orbitando um buraco negro, suas órbitas podem ser usadas para determinar a massa e a localização do buraco negro. Tais observações podem ser usadas para excluir possíveis alternativas, como estrelas de nêutrons. Dessa maneira, os astrônomos identificaram inúmeros candidatos a buracos negros estelares em sistemas binários e estabeleceram que a fonte de rádio conhecida como Sagitário A *, no núcleo da Via Láctea, contém um buraco negro supermassivo de cerca de 4,3 milhões de massas solares.
Em 11 de fevereiro de 2016, a colaboração do LIGO anunciou a primeira detecção direta de ondas gravitacionais, o que também representou a primeira observação de uma fusão de buracos negros.[15] Em dezembro de 2018, foram observados onze ondas gravitacionais originadas de dez buracos negros em fusão (junto com uma fusão binária de estrela de nêutrons).[16][17] Em 10 de abril de 2019, a primeira imagem direta de um buraco negro e sua vizinhança foi publicada, após observações feitas pelo Event Horizon Telescope em 2017 do buraco negro supermassivo no centro galáctico de Messier 87.[3][18][19]
História[editar | editar código-fonte]


A ideia de um corpo tão massivo que nem a luz poderia escapar foi brevemente proposta pelo pioneiro astronômico e clérigo inglês John Michell em uma carta publicada em novembro de 1784. Os cálculos simplistas de Michell supunham que esse corpo pudesse ter a mesma densidade que o Sol e concluíram que esse corpo se formaria quando o diâmetro de uma estrela excedesse o do Sol por um fator de 500 e a velocidade de escape da superfície excedesse a velocidade usual da luz. Michell observou corretamente que esses corpos supermassivos, mas não irradiantes, podem ser detectados por seus efeitos gravitacionais em corpos visíveis próximos.[21][12][22] Os estudiosos da época ficaram inicialmente empolgados com a proposta de que estrelas gigantes, mas invisíveis, pudessem estar escondidas à vista de todos, mas o entusiasmo diminuiu quando a natureza ondulatória da luz se tornou aparente no início do século XIX.[23]
Se a luz fosse uma onda e não um "corpúsculo", não está claro o que, se houver, influenciaria a gravidade na fuga das ondas de luz.[12][22] A relatividade moderna desacredita a noção de Michell de um raio de luz disparando diretamente da superfície de uma estrela supermassiva, sendo desacelerado pela gravidade da estrela, parando e caindo livremente de volta à superfície da estrela.[24]
Relatividade geral[editar | editar código-fonte]
Em 1915, Albert Einstein desenvolveu sua teoria da relatividade geral, tendo demonstrado anteriormente que a gravidade influencia o movimento da luz. Apenas alguns meses depois, Karl Schwarzschild encontrou uma solução para as equações do campo de Einstein, que descrevem o campo gravitacional de uma massa pontual e de uma massa esférica.[25] Alguns meses depois de Schwarzschild, Johannes Droste, um estudante de Hendrik Lorentz, deu a mesma solução para a massa pontual de forma independente e escreveu mais extensivamente sobre suas propriedades.[26][27] Essa solução tinha um comportamento peculiar no que hoje é chamado raio de Schwarzschild, onde se tornou singular, significando que alguns dos termos nas equações de Einstein se tornaram infinitos. A natureza dessa superfície ainda não era totalmente compreendida. Em 1924, Arthur Eddington mostrou que a singularidade desapareceu após uma mudança de coordenadas, embora Georges Lemaître demorasse até 1933 a perceber que isso significava que a singularidade no raio de Schwarzschild era uma singularidade de coordenadas não físicas.[28] Arthur Eddington, no entanto, comentou em um livro de 1926 sobre a possibilidade de uma estrela com massa comprimida no raio de Schwarzschild, observando que a teoria de Einstein nos permite descartar densidades excessivamente grandes para estrelas visíveis como Betelgeuse porque "uma estrela de 250 milhões de quilômetros poderia não ter uma densidade tão alta quanto o Sol. Em primeiro lugar, a força da gravitação seria tão grande que a luz seria incapaz de escapar dela, os raios voltando à estrela como uma pedra na Terra. Em segundo lugar, o desvio para o vermelho das linhas espectrais seria tão grande que o espectro seria retirado da existência. Em terceiro lugar, a massa produziria tanta curvatura da métrica espaço-tempo que o espaço se fecharia ao redor da estrela, deixando-nos do lado de fora (isto é, nenhum lugar).".[29][30]
Em 1931, Subrahmanyan Chandrasekhar calculou, usando relatividade especial, que um corpo não rotativo de matéria degenerada por elétrons acima de uma certa massa limitante (agora chamada de limite de Chandrasekhar em 1,4 massa solar) não possui soluções estáveis.[31] Seus argumentos foram contestados por muitos de seus contemporâneos, como Eddington e Lev Landau, que argumentavam que algum mecanismo ainda desconhecido impediria o colapso.[32] Eles estavam parcialmente corretos: uma anã branca levemente mais massiva que o limite de Chandrasekhar entrará em colapso e se transformará em uma estrela de nêutrons,[33] que é estável em si mesma. Mas em 1939, Robert Oppenheimer e outros previram que as estrelas de nêutrons acima de outro limite (o limite de Tolman-Oppenheimer-Volkoff) entrariam em colapso ainda mais pelas razões apresentadas por Chandrasekhar e concluíram que nenhuma lei da física provavelmente interviria e interromperia pelo menos algumas estrelas do colapsarem em um buracos negros.[34] Seus cálculos originais, baseados no princípio de exclusão de Pauli, deram como 0,7 massa solar; a consideração subsequente de forte repulsão nêutron-nêutron mediada pela força elevou a estimativa para aproximadamente 1,5 a 3,0 massas solares.[35] Observações da fusão da estrela de nêutrons GW170817, que se acredita ter gerado um buraco negro logo depois, refinaram a estimativa do limite de TOV para ~ 2,17 massas solares.[36][37][38][39]
Oppenheimer e seus coautores interpretaram a singularidade na fronteira do raio de Schwarzschild como indicador de que essa era a fronteira de uma bolha na qual o tempo parou. Este é um ponto de vista válido para observadores externos, mas não para observadores que cruzam esse raio. Por causa dessa propriedade, as estrelas colapsadas eram chamadas de "estrelas congeladas", porque um observador externo veria a superfície da estrela congelada no tempo no instante em que seu colapso a levasse ao raio de Schwarzschild.[40]
Era de ouro[editar | editar código-fonte]
Em 1958, David Finkelstein identificou a superfície de Schwarzschild como um horizonte de eventos, "uma perfeita membrana unidirecional: influências causais podem atravessá-la em apenas uma direção".[41] Isso não contradizia estritamente os resultados de Oppenheimer, mas os estendia para incluir o ponto de vista dos observadores que atravessam o horizonte de eventos. A solução proposta por Arthur Stanley Eddington e David Finkelstein estendeu a solução de Schwarzschild para o futuro dos observadores que caem em um buraco negro. Uma extensão completa já havia sido encontrada por Martin Kruskal, que foi instado a publicá-la.[42]
Esses resultados surgiram no início da era de ouro da relatividade geral, marcada pela relatividade geral e pelos buracos negros, tornando-se os principais objetos de pesquisa. Esse processo foi ajudado pela descoberta de pulsares por Jocelyn Bell Burnell em 1967,[43][44] que, em 1969, demonstraram ser estrelas de nêutrons em rotação rápida.[45]
Nesse período, foram encontradas soluções mais gerais de buraco negro. Em 1963, Roy Kerr encontrou a solução exata para um buraco negro em rotação. Dois anos depois, Ezra Newman encontrou a solução axissimétrica para um buraco negro que é rotativo e carregado eletricamente.[46] Através do trabalho de Werner Israel,[47] Brandon Carter[48][49] e David Robinson,[50] o teorema da calvície surgiu, afirmando que uma solução estacionária de buraco negro é completamente descrita pelos três parâmetros da métrica de Kerr-Newman: massa, momento angular e carga elétrica.[51]
Inicialmente, suspeitava-se que as características estranhas das soluções dos buracos negros fossem artefatos patológicos das condições de simetria impostas e que as singularidades não apareciam em situações genéricas. Essa opinião foi defendida em particular por Vladimir Belinsky, Isaak Khalatnikov e Evgeny Lifshitz, que tentaram provar que nenhuma singularidade aparecia em soluções genéricas. No entanto, no final da década de 1960, Roger Penrose[52] e Stephen Hawking usaram técnicas globais para provar que as singularidades aparecem genericamente.[53]
O trabalho de James Bardeen, Jacob Bekenstein, Carter e Hawking no início dos anos 1970 levou à formulação da termodinâmica dos buracos negros.[54] Essas leis descrevem o comportamento de um buraco negro em estreita analogia com as leis da termodinâmica, relacionando massa à energia, área à entropia e gravidade da superfície à temperatura. A analogia foi concluída quando Hawking, em 1974, mostrou que a teoria quântica de campos implica que os buracos negros irradiam como um corpo negro com uma temperatura proporcional à gravidade na superfície do buraco negro, prevendo o efeito agora conhecido como radiação Hawking.[55]
Etimologia[editar | editar código-fonte]
John Michell usou o termo "estrela negra"[56] e, no início do século XX, os físicos usaram o termo "objeto gravitacionalmente colapsado". A escritora científica Marcia Bartusiak relacionou o termo "buraco negro" ao físico Robert H. Dicke, que no início dos anos 1960 comparou o fenômeno ao Buraco Negro de Calcutá, notório como uma prisão onde as pessoas entravam, mas nunca saíam vivas.[57]
O termo "buraco negro" foi usado nas publicações da Life and Science News em 1963[57] e pela jornalista científica Ann Ewing em seu artigo "'Black Holes' in Space", datado de 18 de janeiro de 1964, que era um relatório sobre uma reunião da Associação Americana para o Avanço da Ciência, realizada em Cleveland, nos Estados Unidos.[58][59]
Em dezembro de 1967, um estudante sugeriu a expressão "buraco negro" em uma palestra de John Wheeler;[58] Wheeler adotou o termo por sua brevidade e "valor publicitário",[60] o que levou alguns a atribuírem crédito a Wheeler por cunhar o termo.[61]
Propriedades e estrutura[editar | editar código-fonte]

O teorema da calvície postula que, uma vez atingida uma condição estável após a formação, um buraco negro tem apenas três propriedades físicas independentes: massa, carga e momento angular; o buraco negro é de outra maneira inexpressivo. Se a conjectura for verdadeira, quaisquer dois buracos negros que compartilhem os mesmos valores para essas propriedades ou parâmetros são indistinguíveis um do outro. O grau em que a conjectura é verdadeira para buracos negros reais sob as leis da física moderna é atualmente um problema não resolvido.[51]
Essas propriedades são especiais porque são visíveis do lado de fora de um buraco negro. Por exemplo, um buraco negro carregado repele outras cargas iguais, como qualquer outro objeto carregado. Da mesma forma, a massa total dentro de uma esfera contendo um buraco negro pode ser encontrada usando o análogo gravitacional da lei de Gauss.[62]
Quando um objeto cai em um buraco negro, qualquer informação sobre a forma do objeto ou a distribuição de carga nele é distribuída uniformemente ao longo do horizonte do buraco negro e é perdida para os observadores externos. O comportamento do horizonte nessa situação é um sistema dissipativo que é estreitamente análogo ao de uma membrana elástica condutora com atrito e resistência elétrica — o paradigma da membrana.[63] Isso é diferente de outras teorias de campo, como o eletromagnetismo, que não têm atrito ou resistividade no nível microscópico, porque são reversíveis no tempo. Como um buraco negro atinge um estado estável com apenas três parâmetros, não há como evitar a perda de informações sobre as condições iniciais: os campos gravitacionais e elétricos de um buraco negro fornecem muito pouca informação sobre o que ocorreu. As informações perdidas incluem todas as quantidades que não podem ser medidas distante do horizonte do buraco negro, incluindo números quânticos aproximadamente conservados, como o total do número bariônico e do número leptônico. Esse comportamento é tão intrigante que foi chamado de paradoxo da informação em buracos negros.[64][65]
Propriedades físicas[editar | editar código-fonte]

Os buracos negros estáticos mais simples têm massa, mas não têm nem carga elétrica nem momento angular. Esses buracos negros são frequentemente chamados de buracos negros de Schwarzschild, em homenagem a Karl Schwarzschild, que descobriu essa solução em 1916.[25] Segundo o teorema de Birkhoff, é a única solução a vácuo esfericamente simétrica.[66] Isso significa que não há diferença observável à distância entre o campo gravitacional de um buraco negro e o de qualquer outro objeto esférico da mesma massa. A noção popular de um buraco negro "sugando tudo" em seus arredores é, portanto, correta apenas perto do horizonte de um buraco negro; distante, o campo gravitacional externo é idêntico ao de qualquer outro corpo da mesma massa.[67]
Também existem soluções que descrevem buracos negros mais gerais. Buracos negros carregados sem rotação são descritos pela métrica de Reissner-Nordström, enquanto a métrica de Kerr descreve um buraco negro rotativo sem carga. A solução estacionária mais geral de buraco negro conhecida é a métrica de Kerr-Newman, que descreve um buraco negro com carga e momento angular.[68]
Enquanto a massa de um buraco negro pode assumir qualquer valor positivo, a carga e o momento angular são restringidos pela massa. Nas unidades de Planck, a carga elétrica total Q e o momento angular total J devem satisfazer
para um buraco negro de massa M. Buracos negros com a massa mínima possível que satisfazem essa desigualdade são chamados extremais. Existem soluções das equações de Einstein que violam essa desigualdade, mas elas não possuem um horizonte de eventos. Essas soluções têm as chamadas singularidades nuas, que podem ser observadas do lado de fora e, portanto, são consideradas não físicas. A hipótese da censura cósmica exclui a formação de tais singularidades, quando elas são criadas através do colapso gravitacional da matéria realista.[7] Isso é apoiado por simulações numéricas.[69]
Devido à força relativamente grande do eletromagnetismo, espera-se que os buracos negros formados pelo colapso das estrelas retenham a carga quase neutra da estrela. Espera-se que a rotação seja uma característica universal de objetos astrofísicos compactos. A fonte de raios X binária candidata a buraco negro GRS 1915 + 105[70] parece ter um momento angular próximo ao valor máximo permitido. Esse limite sem carga é[71]
permitindo a definição de um parâmetro de rotação adimensional, tal que[71]
| Classe | Massa aprox. | Raio aprox. |
|---|---|---|
| Buraco negro supermassivo | 105–1010 MSol | 0,001–400 AU |
| Buraco negro de massa intermediária | 103 MSol | 103 km ≈ RTerra |
| Buraco negro estelar | 10 MSol | 30 km |
| Microburaco negro | até MLua | até 0,1 milímetro |
Buracos negros são comumente classificados de acordo com sua massa, independente do momento angular, J. O tamanho de um buraco negro, conforme determinado pelo raio do horizonte de eventos, ou raio de Schwarzschild, é proporcional à massa M, através de
onde rs é o raio de Schwarzschild e MSol é a massa do Sol.[73] Para um buraco negro com rotação diferente de zero e/ou carga elétrica, o raio é menor, até que um buraco negro extremo possa ter um horizonte de eventos próximo a[74]
Horizonte de eventos[editar | editar código-fonte]
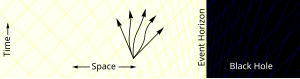
A característica definidora de um buraco negro é o surgimento de um horizonte de eventos — um limite no espaço-tempo através do qual matéria e luz podem passar apenas para dentro em direção à massa do buraco negro. Nada, nem mesmo a luz, pode escapar de dentro do horizonte de eventos. O horizonte de eventos é referido como tal porque se um evento ocorrer dentro dos limites, as informações desse evento não poderão alcançar um observador externo, tornando impossível determinar se esse evento ocorreu.[76]
Como previsto pela relatividade geral, a presença de uma massa deforma o espaço-tempo de tal maneira que os caminhos percorridos pelas partículas se inclinam em direção à massa.[77] No horizonte de eventos de um buraco negro, essa deformação se torna tão forte que não há caminhos que se afastem do buraco negro.[78]
Para um observador distante, os relógios perto de um buraco negro parecem marcar mais lentamente do que os que estão mais distantes do buraco negro.[79] Devido a esse efeito, conhecido como dilatação do tempo gravitacional, um objeto que cai em um buraco negro parece diminuir à medida que se aproxima do horizonte de eventos, levando um tempo infinito para alcançá-lo.[80] Ao mesmo tempo, todos os processos nesse objeto diminuem a velocidade, do ponto de vista de um observador externo fixo, fazendo com que qualquer luz emitida pelo objeto pareça mais vermelha e mais escura, um efeito conhecido como desvio gravitacional para o vermelho.[81] Por fim, o objeto em queda desaparece até não poder mais ser visto. Normalmente, esse processo acontece muito rapidamente, com um objeto desaparecendo da vista em menos de um segundo.[82]
Por outro lado, observadores indestrutíveis que caem em um buraco negro não percebem nenhum desses efeitos à medida que cruzam o horizonte de eventos. De acordo com seus próprios relógios, que lhes parecem marcar normalmente, eles cruzam o horizonte de eventos após um tempo finito sem notar nenhum comportamento singular; na relatividade geral clássica, é impossível determinar a localização do horizonte de eventos a partir de observações locais, devido ao princípio de equivalência de Einstein.[83][84]
A topologia do horizonte de eventos de um buraco negro é sempre aproximadamente esférica.[85][86][87] Para buracos negros não rotativos (estáticos), a geometria do horizonte de eventos é precisamente esférica, enquanto que para buracos negros rotativos o horizonte de eventos é oblato.[88]
Singularidade[editar | editar código-fonte]

No centro de um buraco negro, conforme descrito pela relatividade geral, pode estar uma singularidade gravitacional, uma região onde a curvatura do espaço-tempo se torna infinita.[89] Para um buraco negro não rotativo, essa região assume a forma de um único ponto e, para um buraco negro rotativo, é borrada para formar uma singularidade de anel que fica no plano de rotação.[90] Nos dois casos, a região singular possui volume zero. Também pode ser mostrado que a região singular contém toda a massa da solução do buraco negro.[91] A região singular pode assim ser pensada como tendo densidade infinita.[92]
Observadores que caem em um buraco negro de Schwarzschild (ou seja, que não são rotativos e não são carregados) não podem evitar serem transportados para a singularidade, uma vez que cruzam o horizonte de eventos. Eles podem prolongar a experiência acelerando para desacelerar sua descida, mas apenas até um limite.[93] Quando atingem a singularidade, são esmagados em densidade infinita e sua massa é adicionada ao total do buraco negro. Antes que isso aconteça, eles serão dilacerados pelas crescentes forças das marés em um processo às vezes chamado de espaguetificação ou "efeito macarrão".[94]
No caso de um buraco negro carregado (Reissner–Nordström) ou rotativo (Kerr), é possível evitar a singularidade. Estender essas soluções o máximo possível revela a possibilidade hipotética de sair do buraco negro em um espaço-tempo diferente, com o buraco atuando como um buraco de minhoca.[95] A possibilidade de viajar para outro universo é, no entanto, apenas teórica, pois qualquer perturbação destruiria essa possibilidade.[96] Também parece ser possível seguir curvas fechadas de tipo tempo (retornando ao próprio passado) em torno da singularidade de Kerr, o que leva a problemas de causalidade como o paradoxo do avô.[97] Espera-se que nenhum desses efeitos peculiares sobreviva em um tratamento quântico adequado de buracos negros rotativos e carregados.[98]
O aparecimento de singularidades na relatividade geral é geralmente percebido como sinalizador do colapso da teoria.[99] Esse colapso, no entanto, é esperado; ocorre em uma situação em que os efeitos quânticos devem descrever essas ações, devido à densidade extremamente alta e, portanto, às interações de partículas. Até o momento, não foi possível combinar efeitos quânticos e gravitacionais em uma única teoria, embora existam tentativas de formular tal teoria da gravidade quântica. Geralmente, espera-se que tal teoria não apresente singularidades.[100][101]
Esfera de fótons[editar | editar código-fonte]
A esfera de fótons é um limite esférico de espessura zero, na qual os fótons que se movem tangentes a essa esfera ficam presos em uma órbita circular em torno do buraco negro. Para buracos negros não rotativos, a esfera de fótons tem um raio de 1,5 vez o raio de Schwarzschild. Suas órbitas seriam dinamicamente instáveis, portanto, qualquer pequena perturbação, como uma partícula incidente de matéria, causaria uma instabilidade que aumentaria ao longo do tempo, colocando o fóton em uma trajetória externa, fazendo com que ele escapasse do buraco negro ou em uma espiral interior que o levaria a atravessar o horizonte de eventos em um dado momento.[102]
Embora a luz ainda possa escapar da esfera de fótons, qualquer luz que a atravesse em uma trajetória de entrada será capturada pelo buraco negro. Portanto, qualquer luz que alcance um observador externo da esfera de fótons deve ter sido emitida por objetos entre a esfera de fótons e o horizonte de eventos.[102]
Ergosfera[editar | editar código-fonte]
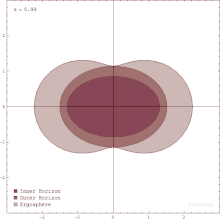
Buracos negros em rotação são cercados por uma região do espaço-tempo na qual é impossível ficar parado, chamada de ergosfera. Este é o resultado de um processo conhecido como arrasto de referenciais; a relatividade geral prevê que qualquer massa em rotação tenderá a "arrastar" levemente ao longo do espaço-tempo imediatamente ao seu redor. Qualquer objeto próximo à massa rotativa tenderá a começar a se mover na direção da rotação. Para um buraco negro rotativo, esse efeito é tão forte perto do horizonte de eventos que um objeto precisaria se mover mais rápido que a velocidade da luz na direção oposta para ficar parado.[104]
A ergosfera de um buraco negro é um volume cujo limite interno é o horizonte de eventos esferoide do buraco negro e um limite externo em forma de abóbora, que coincide com o horizonte de eventos nos polos, mas notavelmente mais amplo ao redor do equador. O limite externo às vezes é chamado de ergossuperfície.[103]
Objetos e radiação podem escapar normalmente da ergosfera. Através do processo Penrose, os objetos podem emergir da ergosfera com mais energia do que entraram. Essa energia é retirada da energia rotacional do buraco negro, causando a desaceleração do último.[105] Uma variação do processo Penrose na presença de fortes campos magnéticos, o processo Blandford-Znajek é considerado um mecanismo provável para a enorme luminosidade e jatos relativísticos de quasares e outros núcleos ativos de galáxias.
Órbita circular estável mais interna (ISCO)[editar | editar código-fonte]
Na gravidade newtoniana, as partículas de teste podem orbitar estavelmente a distâncias arbitrárias de um objeto central. Na relatividade geral, no entanto, existe uma órbita circular estável mais interna (frequentemente chamada de ISCO, sigla em inglês), dentro da qual quaisquer perturbações infinitesimais a uma órbita circular levarão as partículas a espiralar na direção do buraco negro.[106] A localização do ISCO depende da rotação do buraco negro, no caso de um buraco negro de Schwarzschild (rotação zero) é:
e diminui com o aumento da rotação do buraco negro para partículas que orbitam na mesma direção que a rotação.[107]
Formação e evolução[editar | editar código-fonte]
Dado o caráter bizarro dos buracos negros, foi questionado há muito tempo se tais objetos poderiam realmente existir na natureza ou se eram apenas soluções patológicas para as equações de Einstein. O próprio Einstein pensou erroneamente que os buracos negros não se formariam, porque sustentava que o momento angular das partículas em colapso estabilizaria seus movimentos em algum raio.[108] Isso levou a comunidade da relatividade geral a descartar todos os resultados contrários por muitos anos. No entanto, uma minoria de relativistas continuou a afirmar que os buracos negros eram objetos físicos.[109]
Penrose demonstrou que, uma vez que um horizonte de eventos se forme, a relatividade geral sem a mecânica quântica exige que uma singularidade se forme dentro.[52] Logo depois, Hawking mostrou que muitas soluções cosmológicas que descrevem o Big Bang têm singularidades sem campos escalares ou outra matéria exótica (consulte teoremas da singularidade de Penrose-Hawking). A solução de Kerr, o teorema da calvície e as leis da termodinâmica dos buracos negros mostraram que as propriedades físicas dos buracos negros eram simples e compreensíveis, tornando-os assuntos respeitáveis para pesquisa.[110] Buracos negros convencionais são formados pelo colapso gravitacional de objetos pesados, como estrelas, mas também podem, em teoria, ser formados por outros processos.[111][112]
Colapso gravitacional[editar | editar código-fonte]
O colapso gravitacional ocorre quando a pressão interna de um objeto é insuficiente para resistir à sua própria gravidade. Para as estrelas, isso geralmente ocorre porque uma estrela tem muito pouco "combustível" para manter sua temperatura através da nucleossíntese estelar ou porque uma estrela que seria estável recebe matéria extra de uma maneira que não eleva sua temperatura central. Em ambos os casos, a temperatura da estrela não é mais alta o suficiente para impedir que ela entre em colapso com seu próprio peso.[113] O colapso pode ser interrompido pela pressão de degenerescência dos constituintes da estrela, permitindo a condensação da matéria em um estado exótico mais denso. O resultado é um dos vários tipos de estrelas compactas. Quais tipos formam isso depende da massa remanescente da estrela original, deixada depois que as camadas externas foram removidas. Tais explosões e pulsações levam à nebulosa planetária.[114] Essa massa pode ser substancialmente menor que a estrela original. Restos superiores a 5 massas solares são produzidos por estrelas com mais de 20 massas solares antes do colapso.

Se a massa remanescente exceder cerca de 3–4 massas solares (o limite de Tolman-Oppenheimer-Volkoff[34]), seja porque a estrela original era muito massiva ou porque a remanescente coletava massa adicional através da acumulação de matéria, até a pressão de degenerescência dos nêutrons é insuficiente para impedir o colapso. Nenhum mecanismo conhecido (exceto possivelmente a pressão de degeneração dos quarks, veja estrela de quarks) é poderoso o suficiente para parar a implosão e o objeto inevitavelmente entrará em colapso para formar um buraco negro.[113]
Presume-se que o colapso gravitacional de estrelas pesadas seja responsável pela formação de buracos negros de massa estelar. A formação de estrelas no universo primitivo pode ter resultado em estrelas muito massivas, que após o colapso teriam produzido buracos negros de até 10 massas solares. Esses buracos negros podem ser as sementes dos buracos negros supermassivos encontrados no centro da maioria das galáxias.[116] Foi sugerido ainda que buracos negros supermassivos com massas típicas de ~ 10 massas solares poderiam ter se formado a partir do colapso direto das nuvens de gás na fase inicial do universo.[111] Alguns candidatos a esses objetos foram encontrados em observações do universo jovem.
Enquanto a maior parte da energia liberada durante o colapso gravitacional é emitida muito rapidamente, um observador externo na verdade não vê o fim desse processo. Embora o colapso leve uma quantidade finita de tempo a partir do referencial da matéria que cai em direção ao buraco negro, um observador distante verá essa matéria lenta e parada logo acima do horizonte de eventos, devido à dilatação do tempo gravitacional. A luz da matéria em colapso leva cada vez mais tempo para chegar ao observador, com a luz emitida pouco antes da formação do horizonte de eventos atrasar uma quantidade infinita de tempo. Assim, o observador externo nunca vê a formação do horizonte de eventos; em vez disso, a matéria em colapso parece ficar mais escura e cada vez mais deslocada para o vermelho, até que desapareça.[117]
Buracos negros primordiais e o Big Bang[editar | editar código-fonte]
O colapso gravitacional requer grande densidade. Na época atual do universo, essas altas densidades são encontradas apenas nas estrelas, mas no universo inicial, logo após o Big Bang as densidades eram muito maiores, possivelmente permitindo a criação de buracos negros. A alta densidade por si só não é suficiente para permitir a formação de buracos negros, uma vez que uma distribuição uniforme de massa não permitirá que ela se agrupe. Para que os buracos negros primordiais se formassem em um meio tão denso, deve ter havido perturbações iniciais na densidade que poderiam então crescer sob sua própria gravidade. Diferentes modelos para o universo primitivo variam amplamente em suas previsões da escala dessas flutuações. Vários modelos preveem a criação de buracos negros primordiais, variando em tamanho, de uma massa de Planck a centenas de milhares de massas solares.[112]
Apesar de o universo primitivo ser extremamente denso (muito mais denso do que normalmente é necessário para formar um buraco negro), ele não voltou a colapsar em um buraco negro durante o Big Bang. Modelos para o colapso gravitacional de objetos de tamanho relativamente constante, como estrelas, não se aplicam necessariamente da mesma maneira à rápida expansão do espaço, como o Big Bang.[118]
Colisões de alta energia[editar | editar código-fonte]

O colapso gravitacional não é o único processo que pode criar buracos negros. Em princípio, buracos negros podem ser formados em colisões de alta energia que atingem densidade suficiente. A partir de 2002, nenhum desses eventos foi detectado, direta ou indiretamente, como uma deficiência do balanço de massa em experimentos com aceleradores de partículas.[119] Isso sugere que deve haver um limite inferior para a massa de buracos negros. Teoricamente, espera-se que esse limite esteja ao redor da massa de Planck, onde se espera que efeitos quânticos invalidem as previsões da relatividade geral.[120] Isso colocaria a criação de buracos negros firmemente fora do alcance de qualquer processo de alta energia que ocorra na Terra ou próximo a ela. No entanto, certos desenvolvimentos na gravidade quântica sugerem que a massa de Planck poderia ser muito menor: alguns cenários do mundo das P-branas, por exemplo, colocam a fronteira tão baixa quanto 1 TeV/c2.[121] Isso tornaria possível a criação de microburacos negros nas colisões de alta energia que ocorrem quando os raios cósmicos atingem a atmosfera da Terra, ou possivelmente no Large Hadron Collider do CERN. Essas teorias são muito especulativas e a criação de buracos negros nesses processos é considerada improvável por muitos especialistas.[122] Mesmo que microburacos negros pudessem ser formados, espera-se que eles evaporassem em cerca de 10 −25 segundos, não ameaçando a Terra.[123]
Crescimento[editar | editar código-fonte]
Depois que um buraco negro se forma, ele pode continuar a crescer absorvendo matéria adicional. Qualquer buraco negro absorve continuamente gás e poeira interestelar de seus arredores. Esse é o processo principal pelo qual os buracos negros supermassivos parecem ter crescido.[116] Um processo semelhante foi sugerido para a formação de buracos negros de massa intermediária encontrados em aglomerados globulares.[124] Os buracos negros também podem se fundir com outros objetos, como estrelas ou até outros buracos negros. Pensa-se que isso tenha sido importante, especialmente no crescimento inicial de buracos negros supermassivos, que poderiam ter se formado a partir da agregação de muitos objetos menores. O processo também foi proposto como a origem de alguns buracos negros de massa intermediária.[125][126]
Evaporação[editar | editar código-fonte]
Em 1974, Hawking previu que os buracos negros não são totalmente negros, mas emitem pequenas quantidades de radiação térmica;[55] esse efeito ficou conhecido como radiação Hawking. Ao aplicar a teoria quântica de campos a um fundo estático de um buraco negro, ele determinou que um buraco negro deveria emitir partículas que exibissem uma radiação de corpo negro. Desde a publicação de Hawking, muitos outros verificaram o resultado através de várias abordagens.[127] Se a teoria de Hawking da radiação do buraco negro estiver correta, espera-se que os buracos negros encolham e evaporem com o tempo, à medida que perdem massa pela emissão de fótons e outras partículas. A temperatura desse espectro térmico (temperatura de Hawking) é proporcional à gravidade na superfície do buraco negro, que, para um buraco negro de Schwarzschild, é inversamente proporcional à massa. Portanto, grandes buracos negros emitem menos radiação do que pequenos buracos negros.[128]
Um buraco negro estelar de 1 massa solar tem uma temperatura Hawking de 62 nanokelvins.[129] Isso é muito menor do que os 2,7 kelvins da temperatura da radiação cósmica de fundo de microondas. Buracos negros de massa estelar ou maior recebem mais massa do fundo cósmico de microondas do que emitem pela radiação Hawking e, portanto, crescerão em vez de encolher.[130] Para ter uma temperatura Hawking maior que 2,7 K (e conseguir evaporar), um buraco negro precisaria de uma massa menor que a da Lua. Tal buraco negro teria um diâmetro menor que um décimo de milímetro.[131]
Se um buraco negro é muito pequeno, espera-se que os efeitos da radiação se tornem muito fortes. Um buraco negro com a massa de um carro teria um diâmetro de cerca de 10 −24 m e levaria um nanossegundo para evaporar, período durante o qual teria brevemente uma luminosidade superior a 200 vezes a do Sol. Espera-se que os buracos negros de menor massa evaporem ainda mais rápido; por exemplo, um buraco negro de massa 1 TeV / c 2 levaria menos de 10 −88 segundos para evaporar completamente. Para um buraco negro tão pequeno, espera-se que os efeitos da gravitação quântica desempenhem um papel importante e possam hipoteticamente tornar estável um buraco negro tão pequeno, embora os desenvolvimentos atuais na gravidade quântica não indiquem que esse seja o caso.[132][133]
Prevê-se que a radiação Hawking para um buraco negro astrofísico seja muito fraca e, portanto, seria extremamente difícil de detectar a partir da Terra. Uma possível exceção, no entanto, é a explosão de raios gama emitida no último estágio da evaporação de buracos negros primordiais. As pesquisas por esses flashes não tiveram êxito e fornecem limites rigorosos à possibilidade de existência de buracos negros primordiais de baixa massa.[134] O Telescópio Espacial Fermi de raios gama da NASA, lançado em 2008, continuará a busca por esses flashes.[135]
Se os buracos negros evaporarem por meio da radiação Hawking, um buraco negro de massa solar evaporará (começando quando a temperatura do fundo cósmico de microondas cair abaixo da temperatura do buraco negro) durante um período de 1064 anos Um buraco negro supermassivo com uma massa de 1011 (100 bilhões) M evaporará em cerca de 2×10100 anos.[136] Prevê-se que alguns buracos negros monstruosos no universo continuem a crescer até 1014 M durante o colapso dos superaglomerados de galáxias. Mesmo estes evaporariam em uma escala de tempo de até 10106 anos.[137]
Evidência observacional[editar | editar código-fonte]
Por natureza, os próprios buracos negros não emitem nenhuma radiação eletromagnética além da hipotética radiação Hawking, de modo que os astrofísicos que procuram buracos negros geralmente devem confiar em observações indiretas. Por exemplo, a existência de um buraco negro às vezes pode ser inferida observando sua influência gravitacional sobre o ambiente ao redor dele.[138]

O Event Horizon Telescope (EHT), administrado pelo Haystack Observatory do MIT, é um programa ativo que observa diretamente o ambiente imediato do horizonte de eventos dos buracos negros, como o buraco negro no centro da Via Láctea. Em abril de 2017, o EHT iniciou a observação do buraco negro no centro de Messier 87.[139] "No total, oito observatórios de rádio em seis montanhas e quatro continentes observaram a galáxia em Virgo por 10 dias em abril de 2017" para fornecer os dados que renderam a imagem dois anos depois, em abril de 2019.[140] Após dois anos de processamento de dados, a EHT divulgou a primeira imagem direta de um buraco negro, especificamente o buraco negro supermassivo que fica no centro da galáxia acima mencionada.[141][142] O que é visível não é o buraco negro, que se mostra preto por causa da perda de toda a luz nessa região escura, mas sim os gases na borda do horizonte de eventos, exibidos em laranja ou vermelho, que definem a forma do buraco negro.[143]
Pensa-se que o brilho deste material na metade 'inferior' da imagem EHT processada é causado pelo efeito Doppler, pelo qual o material que se aproxima do espectador a velocidades relativísticas é percebido como mais brilhante do que o material que se afasta. No caso de um buraco negro, esse fenômeno implica que o material visível está girando a velocidades relativísticas (>1 000 km/s), as únicas velocidades nas quais é possível equilibrar centrifugamente a imensa atração gravitacional da singularidade e, assim, permanecer em órbita acima do horizonte de eventos. Essa configuração de material brilhante implica que o EHT observou o M87 * de uma perspectiva que captura o disco de acreção do buraco negro quase de ponta a ponta, enquanto todo o sistema girava no sentido horário.[144]
Antes disso, em 2015, o EHT detectou campos magnéticos fora do horizonte de eventos de Sagitário A* e até discerniu algumas de suas propriedades. As linhas de campo que passam pelo disco de acreção foram consideradas uma mistura complexa de ordenadas e emaranhadas. A existência de campos magnéticos havia sido prevista por estudos teóricos de buracos negros.[145][146]
Detecção de ondas gravitacionais da fusão de buracos negros[editar | editar código-fonte]

Em 14 de setembro de 2015, o observatório de ondas gravitacionais LIGO fez a primeira observação direta bem-sucedida de ondas gravitacionais.[15][148] O sinal foi consistente com as previsões teóricas para as ondas gravitacionais produzidas pela fusão de dois buracos negros: um com cerca de 36 massas solares e o outro com 29 massas solares.[149]
Mais importante, o sinal observado pelo LIGO também incluiu o início do toque pós-fusão, o sinal produzido quando um objeto compacto recém-formado se estabiliza em um estado estacionário. Indiscutivelmente, o toque é a maneira mais direta de observar um buraco negro.[150] A partir do sinal LIGO, é possível extrair a frequência e o tempo de amortecimento do modo dominante do toque. A partir disso, é possível inferir a massa e o momento angular do objeto final, que correspondem a previsões independentes a partir de simulações numéricas da fusão.[151] A frequência e o tempo de decaimento do modo dominante são determinados pela geometria da esfera de fótons. Portanto, a observação desse modo confirma a presença de uma esfera de fótons, no entanto, não pode excluir possíveis alternativas exóticas aos buracos negros que são compactos o suficiente para ter uma esfera de fótons.
A observação também fornece a primeira evidência observacional da existência de buracos negros binários de massa estelar. Além disso, é a primeira evidência observacional de buracos negros de massa estelar pesando 25 massas solares ou mais.[152]
Em 15 de junho de 2016, foi anunciada uma segunda detecção de um evento de onda gravitacional em colisão de buracos negros[153] e outros eventos de ondas gravitacionais foram observados desde então.[17]
Movimentos de estrelas orbitando Sagitário A*[editar | editar código-fonte]

Os movimentos de algumas estrelas próximas do centro da Via Láctea fornecem fortes evidências observacionais de que essas estrelas estejam orbitando um buraco negro supermassivo.[154] Desde 1995, os astrônomos acompanham os movimentos de 90 estrelas que orbitam um objeto invisível coincidente com a fonte de rádio Sagitário A*. Ao ajustar suas trajetórias a órbitas keplerianas, os astrônomos foram capazes de inferir, em 1998, que um objeto de 2,6 milhões de massas solares deve ser contido num volume com um raio de 0,02 anos-luz para fazer os movimentos das referidas estrelas.[155] Desde então, uma das estrelas — chamada S2 — completou uma órbita completa. A partir dos dados orbitais, os astrônomos foram capazes de refinar os cálculos da massa de 4,3 milhões de massas solares e um raio de menos de 0,002 anos-luz para o objeto causar o movimento orbital dessas estrelas. O limite superior no tamanho do objeto ainda é muito grande para testar se é menor que o raio de Schwarzschild; no entanto, essas observações sugerem fortemente que o objeto central é um buraco negro supermassivo, pois não há outros cenários plausíveis para confinar tanta massa invisível em um volume tão pequeno. Além disso, existem algumas evidências observacionais de que esse objeto pode possuir um horizonte de eventos, um recurso exclusivo dos buracos negros.[156]
Acreção de matéria[editar | editar código-fonte]

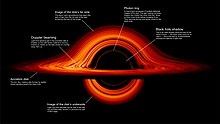
Devido à conservação do momento angular,[158] o gás que cai no poço gravitacional criado por um objeto maciço geralmente forma uma estrutura semelhante a um disco ao redor do objeto. As impressões de artistas, como a representação que acompanha um buraco negro com uma coroa, geralmente descrevem o buraco negro como se fosse um corpo de espaço plano escondendo a parte do disco logo atrás dele, mas, na realidade, as lentes gravitacionais distorceriam bastante a imagem do disco de acreção do buraco negro.[159]
Dentro desse disco, o atrito faria com que o momento angular fosse transportado para fora, permitindo que a matéria caísse ainda mais para dentro, liberando energia potencial e aumentando a temperatura do gás.[160]
Quando o objeto acumulador é uma estrela de nêutrons ou um buraco negro, o gás no disco interno de acumulação orbita em velocidades muito altas devido à sua proximidade com o objeto compacto. O atrito resultante é tão significativo que aquece o disco interno a temperaturas nas quais emite grandes quantidades de radiação eletromagnética (principalmente raios X). Essas fontes brilhantes de raios-X podem ser detectadas por telescópios. Esse processo de acreção é um dos processos de produção de energia mais eficientes conhecidos; até 40% da massa restante do material acumulado pode ser emitida como radiação.[160] (Na fusão nuclear, apenas cerca de 0,7% da massa restante será emitida como energia.) Em muitos casos, os discos de acreção são acompanhados por jatos relativísticos emitidos ao longo dos polos, que consomem grande parte da energia. O mecanismo para a criação desses jatos atualmente não é bem conhecido, em parte devido a dados insuficientes.[161]
Como tal, muitos dos fenômenos mais energéticos do universo foram atribuídos à acumulação de matéria nos buracos negros. Em particular, acredita-se que núcleos e quasares galácticos ativos sejam os discos de acreção de buracos negros supermassivos.[162] Da mesma forma, os binários de raios-X são geralmente aceitos como sistemas estelares binários nos quais uma das duas estrelas é um objeto compacto que agrega matéria de seu companheiro. Também foi sugerido que algumas fontes de raios X ultraluminosas podem ser os discos de acreção de buracos negros de massa intermediária.[163]
Em novembro de 2011, foi relatada a primeira observação direta de um disco de acreção de um quasar ao redor de um buraco negro supermassivo.[164][165]
Binários de raio-X[editar | editar código-fonte]

Os binários de raios-X são sistemas estelares binários que emitem a maior parte de sua radiação na forma de raios-X do espectro. Pensa-se que essas emissões de raios-X resultem quando uma das estrelas (objeto compacto) acumula matéria de outra estrela (regular). A presença de uma estrela comum em tal sistema oferece uma oportunidade para estudar o objeto central e determinar se ele pode ser um buraco negro.[162]
Se esse sistema emitir sinais que podem ser rastreados diretamente de volta ao objeto compacto, não poderá ser um buraco negro. A ausência de tal sinal, no entanto, não exclui a possibilidade de o objeto compacto ser uma estrela de nêutrons. Ao estudar a estrela companheira, muitas vezes é possível obter os parâmetros orbitais do sistema e uma estimativa da massa do objeto compacto. Se for muito maior que o limite de Tolman-Oppenheimer-Volkoff (a massa máxima que uma estrela pode ter sem desmoronar), então o objeto não pode ser uma estrela de nêutrons e geralmente se espera que seja um buraco negro.[162]
O primeiro forte candidato a um buraco negro, Cygnus X-1, foi descoberto por Charles Thomas Bolton,[166] Louise Webster e Paul Murdin[167] em 1972.[168][169] Alguma dúvida, no entanto, permaneceu devido às incertezas resultantes da estrela companheira ser muito mais pesada que o buraco negro candidato. Atualmente, melhores candidatos a buracos negros são encontrados em uma classe de binários de raios-X chamados transientes de raios-X moles. Nesta classe de sistema, a estrela companheira é de massa relativamente baixa, permitindo estimativas mais precisas da massa do buraco negro. Além disso, esses sistemas emitem ativamente raios X por apenas alguns meses, uma vez a cada 10 a 50 anos. Durante o período de baixa emissão de raios X (chamado quiescência), o disco de acreção é extremamente fraco, permitindo observação detalhada da estrela companheira durante esse período. Um dos melhores candidatos é o V404 Cygni.[162]
Quiescência e fluxo de acreção dominado por advecção[editar | editar código-fonte]
Suspeita-se que a fraqueza do disco de acréscimo de um binário de raios-X durante a inatividade seja causada pelo fluxo de massa que entra em um modo chamado fluxo de acreção dominado por advecção (ADAF, sigla em inglês). Nesse modo, quase toda a energia gerada pelo atrito no disco é varrida junto com o fluxo, em vez de ser irradiada. Se esse modelo estiver correto, ele formará fortes evidências qualitativas para a presença de um horizonte de eventos,[170] porque, se o objeto no centro do disco tivesse uma superfície sólida, ele emitiria grandes quantidades de radiação como gás altamente energético. atinge a superfície, um efeito observado para estrelas de nêutrons em um estado semelhante.[160]
Às vezes, as emissões de raios-X dos discos de acúmulo piscam em determinadas frequências. Esses sinais são chamados de oscilações quase periódicas e acredita-se que sejam causados pelo movimento do material ao longo da borda interna do disco de acreção (a órbita circular estável mais interna). Como tal, sua frequência está ligada à massa do objeto compacto. Assim, eles podem ser usados como uma maneira alternativa de determinar a massa de buracos negros candidatos.[171]
Núcleos galácticos[editar | editar código-fonte]

Os astrônomos usam o termo "galáxia ativa" para descrever galáxias com características incomuns, como emissão de linhas espectrais incomuns e emissão de rádio muito forte. Estudos teóricos e observacionais mostraram que a atividade nesses núcleos galácticos ativos (AGN, sigla em inglês) pode ser explicada pela presença de buracos negros supermassivos, que podem ser milhões de vezes mais massivos que os estelares.[172]
Os modelos desses AGN consistem em um buraco negro central que pode ser milhões ou bilhões de vezes mais massivo que o Sol; um disco de gás e poeira chamado disco de acreção; e dois jatos perpendiculares ao disco de acreção.[172][173]
Embora se espere encontrar buracos negros supermassivos na maioria dos AGN, apenas os núcleos de algumas galáxias foram estudados com mais cuidado na tentativa de identificar e medir as massas reais dos candidatos a buracos negros supermassivos centrais. Algumas das galáxias mais notáveis com candidatos a buracos negros supermassivos incluem a Galáxia de Andrômeda, M32, M87, NGC 3115, NGC 3377, NGC 4258, NGC 4889, NGC 1277, OJ 287, APM 08279 + 5255 e a Galáxia do Sombreiro.[174]
Hoje é amplamente aceito que o centro de quase todas as galáxias, não apenas as ativas, contém um buraco negro supermassivo.[175] A estreita correlação observacional entre a massa desse buraco e a dispersão da velocidade da protuberância da galáxia hospedeira, conhecida como relação M-sigma, sugere fortemente uma conexão entre a formação do buraco negro e a própria galáxia.[176]
Microlente (proposto)[editar | editar código-fonte]


Outra maneira de testar a natureza de um buraco negro no futuro é através da observação de efeitos causados por um forte campo gravitacional nas proximidades. Um desses efeitos é a lente gravitacional : a deformação do espaço-tempo em torno de um objeto maciço faz com que os raios de luz sejam desviados tanto quanto a luz que passa através de uma lente óptica. Foram feitas observações de lentes gravitacionais fracas, nas quais os raios de luz são desviados em apenas alguns segundos de arco . No entanto, nunca foi observado diretamente para um buraco negro. Uma possibilidade para observar as lentes gravitacionais por um buraco negro seria observar estrelas em órbita ao redor do buraco negro. Existem vários candidatos para essa observação em órbita em torno de Sagitário A*.[179]
Alternativas[editar | editar código-fonte]
A evidência para buracos negros estelares depende fortemente da existência de um limite superior para a massa de uma estrela de nêutrons. O tamanho desse limite depende muito das suposições feitas sobre as propriedades da matéria densa. Novas fases exóticas da matéria poderiam elevar esse limite.[162] Uma fase de quarks livres em alta densidade pode permitir a existência de estrelas quark densas[180] e alguns modelos supersimétricos preveem a existência de estrelas Q.[181] Algumas extensões do modelo padrão postulam a existência de préons como blocos fundamentais de quarks e leptons, que poderiam hipoteticamente formar estrelas de préon.[182] Esses modelos hipotéticos poderiam potencialmente explicar uma série de observações de candidatos a buracos negros estelares. No entanto, pode ser demonstrado a partir de argumentos na relatividade geral que qualquer objeto desse tipo terá uma massa máxima.
Como a densidade média de um buraco negro dentro de seu raio de Schwarzschild é inversamente proporcional ao quadrado de sua massa, os buracos negros supermassivos são muito menos densos que os buracos negros estelares (a densidade média de 108 massas solares de um buraco negro é comparável com a da água).[162] Consequentemente, a física da matéria que forma um buraco negro supermassivo é muito melhor compreendida e as possíveis explicações alternativas para observações de um buraco negro supermassivo são muito mais mundanas. Por exemplo, um buraco negro supermassivo pode ser modelado por um grande aglomerado de objetos muito escuros. No entanto, essas alternativas geralmente não são estáveis o suficiente para explicar os candidatos a buracos negros supermassivos.
A evidência da existência de buracos negros estelares e supermassivos implica que, para que os buracos negros não se formem, a relatividade geral deve falhar como uma teoria da gravidade, talvez devido ao início de correções mecânicas quânticas. Uma característica muito antecipada de uma teoria da gravidade quântica é que ela não apresentará singularidades ou horizontes de eventos e, portanto, os buracos negros não seriam artefatos reais.[183] Por exemplo, no modelo de fuzzball baseado na teoria das cordas, os estados individuais de uma solução de buraco negro geralmente não têm horizonte de eventos ou singularidade, mas para um observador clássico/semiclássico, a média estatística de tais estados aparece como um ordinário buraco negro deduzido da relatividade geral.[184]
Alguns objetos teóricos foram conjecturados para corresponder às observações de candidatos astronômicos a buracos negros de forma idêntica ou quase idêntica, mas que funcionam por meio de um mecanismo diferente. Isso inclui a gravastar, a estrela negra[185] e a estrela de energia escura.[186]
Perguntas em aberto[editar | editar código-fonte]
Entropia e termodinâmica[editar | editar código-fonte]

Em 1971, Hawking mostrou em condições gerais que a área total dos horizontes de eventos de qualquer coleção de buracos negros clássicos nunca pode diminuir, mesmo que colidam e se fundam.[187] Esse resultado, agora conhecido como a segunda lei da mecânica dos buracos negros, é notavelmente semelhante à segunda lei da termodinâmica, que afirma que a entropia total de um sistema isolado nunca pode diminuir. Assim como os objetos clássicos em temperatura zero absoluta, assumiu-se que os buracos negros tinham entropia zero. Se fosse esse o caso, a segunda lei da termodinâmica seria violada pela matéria carregada de entropia entrando em um buraco negro, resultando em uma diminuição da entropia total do universo. Portanto, Bekenstein propôs que um buraco negro deveria ter uma entropia e ser proporcional à sua área do horizonte.[188]
O vínculo com as leis da termodinâmica foi reforçado pela descoberta de Hawking de que a teoria quântica de campos prevê que um buraco negro irradia radiação do corpo negro a uma temperatura constante. Aparentemente, isso causa uma violação da segunda lei da mecânica dos buracos negros, uma vez que a radiação retira energia do buraco negro, causando seu encolhimento. A radiação, no entanto, também elimina a entropia e pode-se provar, sob suposições gerais, que a soma da entropia da matéria em torno de um buraco negro e um quarto da área do horizonte, medida em unidades de Planck, está sempre aumentando. Isso permite a formulação da primeira lei da mecânica dos buracos negros como um análogo da primeira lei da termodinâmica, com a massa atuando como energia, a gravidade na superfície como temperatura e a área como entropia.[188]
Uma característica intrigante é que a entropia de um buraco negro escala com sua área e não com seu volume, uma vez que a entropia é normalmente uma quantidade extensa que escala linearmente com o volume do sistema. Essa propriedade estranha levou Gerard 't Hooft e Leonard Susskind a propor o princípio holográfico, o que sugere que tudo o que acontece em um volume do espaço-tempo que pode ser descrito por dados na fronteira desse volume.[189]
Embora a relatividade geral possa ser usada para realizar um cálculo semiclássico da entropia do buraco negro, essa situação é teoricamente insatisfatória. Na mecânica estatística, a entropia é entendida como a contagem do número de configurações microscópicas de um sistema que possui as mesmas qualidades macroscópicas (como massa, carga, pressão etc.) Sem uma teoria satisfatória da gravidade quântica, não se pode realizar tal cálculo para buracos negros. Algum progresso foi feito em várias abordagens da gravidade quântica. Em 1995, Andrew Strominger e Cumrun Vafa mostraram que a contagem dos microestados de um buraco negro supersimétrico específico na teoria das cordas reproduzia a entropia de Bekenstein-Hawking.[190] Desde então, resultados semelhantes foram relatados para diferentes buracos negros, tanto na teoria das cordas quanto em outras abordagens da gravidade quântica, como a gravidade quântica em loop.[191]
Paradoxo da perda de informações[editar | editar código-fonte]
A informação física é perdida em um buraco negro?
Como um buraco negro possui apenas alguns parâmetros internos, a maioria das informações sobre a matéria que foi usada para formar o buraco negro é perdida. Independentemente do tipo de matéria que entra em um buraco negro, parece que apenas as informações relativas à massa total, carga e momento angular são conservadas. Enquanto se pensava que os buracos negros persistissem para sempre, essa perda de informação não é tão problemática, pois pode-se pensar que a informação existe dentro do buraco negro, inacessível do lado de fora, mas representada no horizonte de eventos de acordo com o princípio holográfico. No entanto, os buracos negros evaporam lentamente emitindo radiação Hawking. Essa radiação parece não conter nenhuma informação adicional sobre o assunto que formou o buraco negro, o que significa que essa informação parece ter desaparecido para sempre.[192]
A questão de saber se a informação é realmente perdida nos buracos negros (o paradoxo da informação sobre os buracos negros) dividiu a comunidade teórica da física. Na mecânica quântica, a perda de informações corresponde à violação de propriedades vitais denominada unitariedade, que tem a ver com a conservação da probabilidade. Argumentou-se que a perda de unidade também implicaria violação da conservação de energia.[193] Nos últimos anos, foram construídas evidências de que, de fato, a informação e a unitariedade são preservadas em um tratamento gravitacional quântico completo do problema.[194]
Paradoxo do firewall[editar | editar código-fonte]
De acordo com a teoria quântica de campos no espaço-tempo curvo, uma única emissão de radiação Hawking envolve duas partículas mutuamente entrelaçadas. A partícula de saída escapa e é emitida como um quantum de radiação Hawking; a partícula que se dirige ao buraco negro é engolida por ele. Suponha que um buraco negro formou um tempo finito no passado e evapore completamente em algum tempo finito no futuro. Então, ele emitirá apenas uma quantidade finita de informações codificadas dentro da radiação Hawking. Suponha que no momento , mais da metade das informações já foram emitidas. De acordo com pesquisas amplamente aceitas por físicos como Don Page[195][196] e Leonard Susskind, uma partícula emitida no momento deve estar emaranhada com toda a radiação Hawking que o buraco negro emitiu anteriormente. Isso cria um paradoxo: um princípio chamado "monogamia do enredamento" exige que, como qualquer sistema quântico, a partícula que sai não possa ser totalmente enredada com dois sistemas independentes ao mesmo tempo; no entanto, aqui a partícula de saída parece estar enredada tanto com a partícula que entra quanto, independentemente, com a radiação Hawking do passado.[197]
Para resolver o paradoxo, os físicos podem eventualmente ser forçados a desistir de uma das três teorias testadas pelo tempo: princípio da equivalência de Einstein, unitariedade ou teoria quântica de campos existente. Uma solução possível, que viola o princípio da equivalência, é que uma parede de fogo ("firewall") destrói as partículas recebidas no horizonte de eventos.[198] Uma análise de 2016 dos dados do LIGO mostra sinais experimentais de ecos causados por um horizonte de eventos nebulosos; esses ecos podem ser possíveis nas teorias do firewall ou do fuzzball, mas não devem ocorrer na relatividade geral clássica. Nos próximos dois anos, dados adicionais do LIGO devem estabelecer se os ecos eram apenas ruído aleatório ou se são, em vez disso, evidência de uma violação da relatividade geral clássica.[199]
Ver também[editar | editar código-fonte]
Referências
- ↑ Oldham, L. J. «Galaxy structure from multiple tracers – II. M87 from parsec to megaparsec scales». Monthly Notices of the Royal Astronomical Society. 457: 421–439. Bibcode:2016MNRAS.457..421O. arXiv:1601.01323
 . doi:10.1093/mnras/stv2982
. doi:10.1093/mnras/stv2982
- ↑ «Black Hole Picture Revealed for the First Time – Astronomers at last have captured an image of the darkest entities in the cosmos – Comments». The New York Times. Consultado em 10 de março de 2020
- ↑ a b «First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole». The Astrophysical Journal. 87 (1): L1. Bibcode:2019ApJ...875L...1E. doi:10.3847/2041-8213/ab0ec7
- ↑ «Black Hole Image Makes History». NASA. Consultado em 10 de março de 2020
- ↑ «The woman behind first black hole image». BBC News. Consultado em 10 de março de 2020
- ↑ Wald 1984, pp. 299–300
- ↑ a b Wald, R. M. (1997). «Gravitational Collapse and Cosmic Censorship». In: Iyer, B. R.; Bhawal, B. Black Holes, Gravitational Radiation and the Universe. Springer. [S.l.: s.n.] pp. 69–86. ISBN 978-9401709347. arXiv:gr-qc/9710068
 . doi:10.1007/978-94-017-0934-7
. doi:10.1007/978-94-017-0934-7
- ↑ «Black Hole Hunters». NASA. Consultado em 10 de março de 2020
- ↑ «Introduction to Black Holes». socratease.in. Consultado em 10 de março de 2020
- ↑ Schutz, Bernard F. (2003). Gravity from the ground up. Cambridge University Press. [S.l.: s.n.] ISBN 978-0-521-45506-0
- ↑ Davies. «Thermodynamics of Black Holes» (PDF). Reports on Progress in Physics. 41: 1313–1355. Bibcode:1978RPPh...41.1313D. doi:10.1088/0034-4885/41/8/004. Consultado em 12 de março de 2020
- ↑ a b c «Michell, Laplace and the origin of the black hole concept». Journal of Astronomical History and Heritage. 12: 90–96. 2009. Bibcode:2009JAHH...12...90M
- ↑ «Not Just Dying Stars: A Black Hole That Came From Gas». Science Friday (em inglês). Consultado em 12 de novembro de 2023
- ↑ FM, Player (10 de novembro de 2023), 646: Euclid Telescope’s First Images | A Black Hole That Came From Gas (em inglês), consultado em 12 de novembro de 2023
- ↑ a b Abbott, B.P.; et al. (2016). «Observation of Gravitational Waves from a Binary Black Hole Merger». Phys. Rev. Lett. 116. 061102 páginas. Bibcode:2016PhRvL.116f1102A. PMID 26918975. arXiv:1602.03837
 . doi:10.1103/PhysRevLett.116.061102
. doi:10.1103/PhysRevLett.116.061102
- ↑ Siegel, Ethan. «Five Surprising Truths About Black Holes From LIGO». Forbes
- ↑ a b «Detection of gravitational waves». LIGO. Consultado em 10 de março de 2020
- ↑ Bouman, Katherine L.; Johnson, Michael D.; Zoran, Daniel; Fish, Vincent L.; Doeleman, Sheperd S.; Freeman (2016). «Computational Imaging for VLBI Image Reconstruction». 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). [S.l.: s.n.] pp. 913–922. ISBN 978-1-4673-8851-1. arXiv:1512.01413
 . doi:10.1109/CVPR.2016.105
. doi:10.1109/CVPR.2016.105
- ↑ «When a Black Hole Finally Reveals Itself, It Helps to Have Our Very Own Cosmic Reporter – Astronomers announced Wednesday that they had captured the first image of a black hole. The Times's Dennis Overbye answers readers' questions.». The New York Times. Consultado em 10 de março de 2020
- ↑ «Ripped Apart by a Black Hole». ESO Press Release
- ↑ Michell. «On the Means of Discovering the Distance, Magnitude, &c. of the Fixed Stars, in Consequence of the Diminution of the Velocity of Their Light, in Case Such a Diminution Should be Found to Take Place in any of Them, and Such Other Data Should be Procured from Observations, as Would be Farther Necessary for That Purpose. By the Rev. John Michell, B. D. F. R. S. In a Letter to Henry Cavendish, Esq. F. R. S. and A. S». Philosophical Transactions of the Royal Society. 74: 35–57. Bibcode:1784RSPT...74...35M. JSTOR 106576. doi:10.1098/rstl.1784.0008
- ↑ a b Thorne 1994, pp. 123–124
- ↑ Slayter, Elizabeth M.; Slayter, Henry S. (1992). Light and Electron Microscopy. Cambridge University Press. [S.l.: s.n.] ISBN 978-0-521-33948-3
- ↑ «Light escaping from black holes». Universidade de Cambridge. Consultado em 12 de março de 2020
- ↑ a b Schwarzschild. «Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie». Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. 7: 189–196. Bibcode:1916SPAW.......189S
- ↑ Droste. «On the field of a single centre in Einstein's theory of gravitation, and the motion of a particle in that field» (PDF). Proceedings Royal Academy Amsterdam. 19: 197–215
- ↑ Kox, A. J. (1992). «General Relativity in the Netherlands: 1915–1920». In: Eisenstaedt; Kox. Studies in the history of general relativity. Birkhäuser. [S.l.: s.n.] ISBN 978-0-8176-3479-7
- ↑ 't Hooft. «Introduction to the Theory of Black Holes» (PDF): 47–48
- ↑ Eddington, Arthur (1926). The Internal Constitution of the Stars. Cambridge University Press. [S.l.: s.n.] ISBN 978-0-521-33708-3
- ↑ Thorne, Kip S.; Hawking, Stephen (1994). Black Holes and Time Warps: Einstein's Outrageous Legacy. W. W. Norton & Company. [S.l.: s.n.] pp. 134–135. ISBN 978-0-393-31276-8
- ↑ Venkataraman, G. (1992). Chandrasekhar and his limit. Universities Press. [S.l.: s.n.] ISBN 978-81-7371-035-3
- ↑ Detweiler. «Resource letter BH-1: Black holes». American Journal of Physics. 49: 394–400. Bibcode:1981AmJPh..49..394D. doi:10.1119/1.12686
- ↑ Harpaz, A. (1994). Stellar evolution. A K Peters, Ltd. [S.l.: s.n.] ISBN 978-1-56881-012-6
- ↑ a b Oppenheimer. «On Massive Neutron Cores». Physical Review. 55: 374–381. Bibcode:1939PhRv...55..374O. doi:10.1103/PhysRev.55.374
- ↑ Bombaci. «The Maximum Mass of a Neutron Star». Astronomy and Astrophysics. 305: 871–877. Bibcode:1996A&A...305..871B
- ↑ Cho. «A weight limit emerges for neutron stars». Science. 359: 724–725. Bibcode:2018Sci...359..724C. PMID 29449468. doi:10.1126/science.359.6377.724
- ↑ «Constraining the Maximum Mass of Neutron Stars from Multi-messenger Observations of GW170817». The Astrophysical Journal. 850. Bibcode:2017ApJ...850L..19M. arXiv:1710.05938
 . doi:10.3847/2041-8213/aa991c
. doi:10.3847/2041-8213/aa991c
- ↑ «Modeling GW170817 based on numerical relativity and its implications». Physical Review D. 96. 123012 páginas. Bibcode:2017PhRvD..96l3012S. arXiv:1710.07579
 . doi:10.1103/PhysRevD.96.123012
. doi:10.1103/PhysRevD.96.123012
- ↑ «Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars». Astrophysical Journal. 852: L25. Bibcode:2018ApJ...852L..25R. arXiv:1711.00314
 . doi:10.3847/2041-8213/aaa401
. doi:10.3847/2041-8213/aaa401
- ↑ Ruffini. «Introducing the black hole» (PDF). Physics Today. 24: 30–41. Bibcode:1971PhT....24a..30R. doi:10.1063/1.3022513
- ↑ Finkelstein. «Past-Future Asymmetry of the Gravitational Field of a Point Particle». Physical Review. 110: 965–967. Bibcode:1958PhRv..110..965F. doi:10.1103/PhysRev.110.965
- ↑ «Maximal Extension of Schwarzschild Metric». Physical Review. 119. Bibcode:1960PhRv..119.1743K. doi:10.1103/PhysRev.119.1743
- ↑ «Observation of a Rapidly Pulsating Radio Source». Nature. 217: 709–713. Bibcode:1968Natur.217..709H. doi:10.1038/217709a0
- ↑ «Observations of some further Pulsed Radio Sources». Nature. 218: 126–129. Bibcode:1968Natur.218..126P. doi:10.1038/218126a0
- ↑ Hewish. «Pulsars». Annual Review of Astronomy and Astrophysics. 8: 265–296. Bibcode:1970ARA&A...8..265H. doi:10.1146/annurev.aa.08.090170.001405
- ↑ «Metric of a Rotating, Charged Mass». Journal of Mathematical Physics. 6. Bibcode:1965JMP.....6..918N. doi:10.1063/1.1704351
- ↑ Israel. «Event Horizons in Static Vacuum Space-Times». Physical Review. 164. Bibcode:1967PhRv..164.1776I. doi:10.1103/PhysRev.164.1776
- ↑ Carter. «Axisymmetric Black Hole Has Only Two Degrees of Freedom». Physical Review Letters. 26. Bibcode:1971PhRvL..26..331C. doi:10.1103/PhysRevLett.26.331
- ↑ Carter, B. (1977). «The vacuum black hole uniqueness theorem and its conceivable generalisations». Proceedings of the 1st Marcel Grossmann meeting on general relativity. [S.l.: s.n.] pp. 243–254
- ↑ «Uniqueness of the Kerr Black Hole». Physical Review Letters. 34. Bibcode:1975PhRvL..34..905R. doi:10.1103/PhysRevLett.34.905
- ↑ a b Heusler. «Stationary Black Holes: Uniqueness and Beyond». Living Reviews in Relativity. 15. 7 páginas. Bibcode:2012LRR....15....7C. PMC 5255892
 . PMID 28179837. arXiv:1205.6112
. PMID 28179837. arXiv:1205.6112 . doi:10.12942/lrr-2012-7
. doi:10.12942/lrr-2012-7
- ↑ a b «Gravitational Collapse and Space-Time Singularities». Physical Review Letters. 14. Bibcode:1965PhRvL..14...57P. doi:10.1103/PhysRevLett.14.57
- ↑ «The Classical Singularity Theorems and Their Quantum Loopholes». International Journal of Theoretical Physics. 42. doi:10.1023/A:1025754515197
- ↑ «The four laws of black hole mechanics». Communications in Mathematical Physics. 31: 161–170. Bibcode:1973CMaPh..31..161B. MR 0334798. Zbl 1125.83309. doi:10.1007/BF01645742
- ↑ a b Hawking. «Black hole explosions?». Nature. 248: 30–31. Bibcode:1974Natur.248...30H. doi:10.1038/248030a0
- ↑ Popova, Maria. «Mapping the Heavens: How Cosmology Shaped Our Understanding of the Universe and the Strange Story of How the Term "Black Hole" Was Born». brainpickings.org. Consultado em 10 de março de 2020
- ↑ a b «MIT's Marcia Bartusiak On Understanding Our Place In The Universe». www.wbur.org. Consultado em 10 de março de 2020
- ↑ a b «50 years later, it's hard to say who named black holes». Science News. Consultado em 10 de março de 2020
- ↑ «Ann E. Ewing, journalist first reported black holes». Boston.com. Consultado em 10 de março de 2020
- ↑ «Pioneering Physicist John Wheeler Dies at 96». Scientific American. Consultado em 10 de março de 2020
- ↑ «John A. Wheeler, Physicist Who Coined the Term 'Black Hole,' Is Dead at 96». The New York Times. Consultado em 10 de março de 2020
- ↑ Carroll 2004, p. 253
- ↑ Thorne, K. S.; Price, R. H. (1986). Black holes: the membrane paradigm. Yale University Press. [S.l.: s.n.] ISBN 978-0-300-03770-8
- ↑ Anderson, Warren G. «The Black Hole Information Loss Problem». Usenet Physics FAQ. Consultado em 10 de março de 2020
- ↑ Caltech (ed.). Black holes (PDF). Consultado em 10 de março de 2020
- ↑ Hawking & Ellis 1973, Appendix B
- ↑ Seeds, Michael A.; Backman, Dana E. (2007). Perspectives on Astronomy. Cengage Learning. [S.l.: s.n.] ISBN 978-0-495-11352-2
- ↑ Shapiro, S. L.; Teukolsky, S. A. (1983). Black holes, white dwarfs, and neutron stars: the physics of compact objects. John Wiley and Sons. [S.l.: s.n.] ISBN 978-0-471-87316-7
- ↑ Berger. «Numerical Approaches to Spacetime Singularities». Living Reviews in Relativity. 5: 2002–1. Bibcode:2002LRR.....5....1B. PMC 5256073
 . PMID 28179859. arXiv:gr-qc/0201056
. PMID 28179859. arXiv:gr-qc/0201056 . doi:10.12942/lrr-2002-1
. doi:10.12942/lrr-2002-1
- ↑ «The Spin of the Near-Extreme Kerr Black Hole GRS 1915+105». Astrophysical Journal. 652: 518–539. Bibcode:2006ApJ...652..518M. arXiv:astro-ph/0606076
 . doi:10.1086/508457
. doi:10.1086/508457
- ↑ a b c Abbott. «GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2». Physical Review Letters. 118. 221101 páginas. Bibcode:2017PhRvL.118v1101A. PMID 28621973. arXiv:1706.01812
 . doi:10.1103/PhysRevLett.118.221101
. doi:10.1103/PhysRevLett.118.221101
- ↑ Abbott, B. P.; et al. (LIGO Scientific Collaboration & Virgo Collaboration) (16 de outubro de 2017). «GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral». Physical Review Letters. 119 (16). 161101 páginas. Bibcode:2017PhRvL.119p1101A. PMID 29099225. arXiv:1710.05832
 . doi:10.1103/PhysRevLett.119.161101
. doi:10.1103/PhysRevLett.119.161101
- ↑ Wald 1984, pp. 124–125
- ↑ «Destroying a near-extremal Kerr–Newman black hole». Physical Review D. 84. 027501 páginas. Bibcode:2011PhRvD..84b7501S. arXiv:1105.3950
 . doi:10.1103/PhysRevD.84.027501
. doi:10.1103/PhysRevD.84.027501
- ↑ Misner, Thorne & Wheeler 1973, p. 848
- ↑ Wheeler 2007, p. 179
- ↑ Carroll 2004, Ch. 5.4 and 7.3
- ↑ «Singularities and Black Holes > Lightcones and Causal Structure». Stanford Encyclopedia of Philosophy. Consultado em 10 de março de 2020
- ↑ Carroll 2004, p. 217
- ↑ Carroll 2004, p. 218
- ↑ «Inside a black hole». Knowing the universe and its secrets. Consultado em 10 de março de 2020
- ↑ «What happens to you if you fall into a black holes». John Baez. Consultado em 10 de março de 2020
- ↑ Carroll 2004, p. 222
- ↑ National Geographic (ed.). «Watch: Three Ways an Astronaut Could Fall Into a Black Hole». Consultado em 12 de março de 2020
- ↑ Emparan, R.; Reall, H. S. (2008). «Black Holes in Higher Dimensions». Living Reviews in Relativity. 11 (6). 6 páginas. Bibcode:2008LRR....11....6E. PMC 5253845
 . PMID 28163607. arXiv:0801.3471
. PMID 28163607. arXiv:0801.3471 . doi:10.12942/lrr-2008-6
. doi:10.12942/lrr-2008-6
- ↑ Obers, N. A. (2009). Papantonopoulos, Eleftherios, ed. Black Holes in Higher-Dimensional Gravity (PDF). Physics of Black Holes. Col: Lecture Notes in Physics. 769. [S.l.: s.n.] pp. 211–258. Bibcode:2009LNP...769.....P. ISBN 978-3-540-88459-0. arXiv:0802.0519
 . doi:10.1007/978-3-540-88460-6
. doi:10.1007/978-3-540-88460-6
- ↑ hawking & ellis 1973, Ch. 9.3
- ↑ «Toroidal black holes and topological censorship» (PDF). Physical Review D. 52: 6982–6987. Bibcode:1995PhRvD..52.6982S. doi:10.1103/PhysRevD.52.6982
- ↑ Carroll 2004, p. 205
- ↑ Carroll 2004, pp. 264–265
- ↑ Carroll 2004, p. 252
- ↑ «Sizes of Black Holes? How Big is a Black Hole?». Sky & Telescope
- ↑ Lewis. «No Way Back: Maximizing Survival Time Below the Schwarzschild Event Horizon». Publications of the Astronomical Society of Australia. 24: 46–52. Bibcode:2007PASA...24...46L. arXiv:0705.1029
 . doi:10.1071/AS07012
. doi:10.1071/AS07012
- ↑ Wheeler 2007, p. 182
- ↑ Carroll 2004, pp. 257–259 and 265–266
- ↑ «Black holes: the inside story». Physics World. 9: 34–37. Bibcode:1996PhyW....9...34D. doi:10.1088/2058-7058/9/1/26. Consultado em 12 de março de 2020
- ↑ Carroll 2004, p. 266
- ↑ «Internal structure of black holes». Physical Review D. 41. Bibcode:1990PhRvD..41.1796P. doi:10.1103/PhysRevD.41.1796
- ↑ Wald 1984, p. 212
- ↑ Hamade, R. Universidade de Cambridge, ed. «Black Holes and Quantum Gravity». Cambridge Relativity and Cosmology. Consultado em 10 de março de 2020
- ↑ Palmer, D. «Ask an Astrophysicist: Quantum Gravity and Black Holes». NASA
- ↑ a b «Shadows of colliding black holes». Physical Review D. 84. 063008 páginas. Bibcode:2011PhRvD..84f3008N. arXiv:1106.2425
 . doi:10.1103/PhysRevD.84.063008
. doi:10.1103/PhysRevD.84.063008
- ↑ a b «The Kerr spacetime: A brief introduction». arXiv:0706.0622
 , página 35, Fig. 3
, página 35, Fig. 3
- ↑ Carroll 2004, Ch. 6.6
- ↑ Carroll 2004, Ch. 6.7
- ↑ Thorne, Misner & Wheeler 1973
- ↑ «Rotating black holes: locally nonrotating frames, energy extraction, and scalar synchrotron radiation». The Astrophysical Journal. 178: 347–370. Bibcode:1972ApJ...178..347B. doi:10.1086/151796
- ↑ Einstein. «On A Stationary System With Spherical Symmetry Consisting of Many Gravitating Masses». Annals of Mathematics. 40: 922–936. JSTOR 1968902. doi:10.2307/1968902
- ↑ Kerr, R. P. (2009). «The Kerr and Kerr-Schild metrics». In: Wiltshire; Visser; Scott. The Kerr Spacetime. Cambridge University Press. [S.l.: s.n.] Bibcode:2007arXiv0706.1109K. ISBN 978-0-521-88512-6. arXiv:0706.1109

- ↑ Hawking. «The Singularities of Gravitational Collapse and Cosmology». Proceedings of the Royal Society A. 314: 529–548. Bibcode:1970RSPSA.314..529H. JSTOR 2416467. doi:10.1098/rspa.1970.0021
- ↑ a b «First Identification of Direct Collapse Black Hole Candidates in the Early Universe in CANDELS/GOODS-S». Mon. Not. R. Astron. Soc. 459. 1432 páginas. 2016. Bibcode:2016MNRAS.459.1432P. arXiv:1603.08522
 . doi:10.1093/mnras/stw725
. doi:10.1093/mnras/stw725
- ↑ a b Carr, B. J. (2005). «Primordial Black Holes: Do They Exist and Are They Useful?». In: Suzuki; Yokoyama; Suto; Sato. Inflating Horizon of Particle Astrophysics and Cosmology. Universal Academy Press. [S.l.: s.n.] pp. astro–ph/0511743. Bibcode:2005astro.ph.11743C. ISBN 978-4-946443-94-7. arXiv:astro-ph/0511743

- ↑ a b Carroll 2004, Section 5.8
- ↑ Griffiths, Martin (2012). Planetary Nebulae and How to Observe Them. Springer Science & Business Media (em inglês). [S.l.: s.n.] p. 11. ISBN 978-1-4614-1781-1
- ↑ «Artist's impression of supermassive black hole seed»
- ↑ a b Rees, M. J.; Volonteri, M. (2007). «Massive black holes: formation and evolution». In: Karas; Matt. Black Holes from Stars to Galaxies – Across the Range of Masses. 238. [S.l.: s.n.] pp. 51–58. Bibcode:2007IAUS..238...51R. ISBN 978-0-521-86347-6. arXiv:astro-ph/0701512
 . doi:10.1017/S1743921307004681
. doi:10.1017/S1743921307004681
- ↑ «Gravitational Collapse: The Role of General Relativity» (PDF). General Relativity and Gravitation. 34. Bibcode:2002GReGr..34.1141P. doi:10.1023/A:1016578408204
- ↑ «Is the Big Bang a black hole?». John Baez
- ↑ Giddings. «High energy colliders as black hole factories: The end of short distance physics». Physical Review D. 65. Bibcode:2002PhRvD..65e6010G. arXiv:hep-ph/0106219
 . doi:10.1103/PhysRevD.65.056010
. doi:10.1103/PhysRevD.65.056010
- ↑ «Is there a black hole minimum mass?». Physical Review D. 74. Bibcode:2006PhRvD..74h4004H. arXiv:gr-qc/0609055
 . doi:10.1103/PhysRevD.74.084004
. doi:10.1103/PhysRevD.74.084004
- ↑ Arkani–Hamed. «The hierarchy problem and new dimensions at a millimeter». Physics Letters B. 429: 263–272. Bibcode:1998PhLB..429..263A. arXiv:hep-ph/9803315
 . doi:10.1016/S0370-2693(98)00466-3
. doi:10.1016/S0370-2693(98)00466-3
- ↑ LHC Safety Assessment Group (2008). «Review of the Safety of LHC Collisions» (PDF). Journal of Physics G: Nuclear Physics. 35. 115004 páginas. Bibcode:2008JPhG...35k5004E. arXiv:0806.3414
 . doi:10.1088/0954-3899/35/11/115004
. doi:10.1088/0954-3899/35/11/115004
- ↑ Cavaglià. «Particle accelerators as black hole factories?». Einstein-Online. 4
- ↑ «Intermediate-Mass Black Holes in Early Globular Clusters». The Astrophysical Journal Letters. 713: L41–L44. Bibcode:2010ApJ...713L..41V. arXiv:1003.3470
 . doi:10.1088/2041-8205/713/1/L41
. doi:10.1088/2041-8205/713/1/L41
- ↑ «Formation of massive black holes through runaway collisions in dense young star clusters». Nature. 428: 724–726. Bibcode:2004Natur.428..724P. PMID 15085124. arXiv:astro-ph/0402622
 . doi:10.1038/nature02448
. doi:10.1038/nature02448
- ↑ «Binary Mergers and Growth of Black Holes in Dense Star Clusters». The Astrophysical Journal. 637: 937–951. Bibcode:2006ApJ...637..937O. arXiv:astro-ph/0508224
 . doi:10.1086/498446
. doi:10.1086/498446
- ↑ Page. «Hawking radiation and black hole thermodynamics». New Journal of Physics. 7. Bibcode:2005NJPh....7..203P. arXiv:hep-th/0409024
 . doi:10.1088/1367-2630/7/1/203
. doi:10.1088/1367-2630/7/1/203
- ↑ Carroll 2004, Ch. 9.6
- ↑ «Ask Ethan: Do Black Holes Grow Faster Than They Evaporate?». Forbes ("Starts With A Bang" blog). Consultado em 12 de março de 2020
- ↑ «Black hole Hawking radiation may never be observed!». General Relativity and Gravitation. 33: 175–181. Bibcode:2001GReGr..33..175S. doi:10.1023/A:1002753400430
- ↑ Max Planck Institute for Gravitational Physics (ed.). «Evaporating black holes?». Einstein online. Consultado em 10 de março de 2020. Cópia arquivada em 23 de junho de 2012
- ↑ «Astrophysical implications of hypothetical stable TeV-scale black holes». Physical Review D. 78. Bibcode:2008PhRvD..78c5009G. arXiv:0806.3381
 . doi:10.1103/PhysRevD.78.035009
. doi:10.1103/PhysRevD.78.035009
- ↑ «The end of the world at the Large Hadron Collider?». Physics. 1. Bibcode:2008PhyOJ...1...14P. doi:10.1103/Physics.1.14
- ↑ «Search of the energetic gamma-ray experiment telescope (EGRET) data for high-energy gamma-ray microsecond bursts». Astrophysical Journal. 434: 557–559. Bibcode:1994ApJ...434..557F. doi:10.1086/174758
- ↑ Naeye, R. «Testing Fundamental Physics». NASA
- ↑ Particle emission rates from a black hole: Massless particles from an uncharged, nonrotating hole, Don N. Page, Physical Review D 13 (1976), pp. 198–206. doi:10.1103/PhysRevD.13.198. See in particular equation (27).
- ↑ «Entropy in an Expanding Universe». Science. 217: 593–599. 1982. Bibcode:1982Sci...217..593F. PMID 17817517. doi:10.1126/science.217.4560.593 See page 596: table 1 and section "black hole decay" and previous sentence on that page.
- ↑ «Black Holes | Science Mission Directorate». NASA. Consultado em 12 de março de 2020
- ↑ «Abril de 2017 Observations». Event Horizon Telescope. Consultado em 12 de março de 2020
- ↑ «Darkness Visible, Finally: Astronomers Capture First Ever Image of a Black Hole». The New York Times. Consultado em 12 de março de 2020
- ↑ AP. «Astronomers Reveal the First Picture of a Black Hole». The New York Times. Consultado em 12 de março de 2020
- ↑ Doeleman, Shep. «The Event Horizon Telescope: Imaging and Time-Resolving a Black Hole». Physics @ Berkeley. Consultado em 12 de março de 2020
- ↑ «The first picture of a black hole opens a new era of astrophysics». Science News. Consultado em 12 de março de 2020
- ↑ «The first picture of a black hole opens a new era of astrophysics». Science News (em inglês). Consultado em 12 de março de 2020
- ↑ Johnson. «Resolved magnetic-field structure and variability near the event horizon of Sagittarius A*». Science. 350: 1242–1245. Bibcode:2015Sci...350.1242J. PMID 26785487. arXiv:1512.01220
 . doi:10.1126/science.aac7087
. doi:10.1126/science.aac7087
- ↑ «Event Horizon Telescope Reveals Magnetic Fields at Milky Way's Central Black Hole». cfa.harvard.edu. Consultado em 12 de março de 2020
- ↑ O. Straub, F.H. Vincent, M.A. Abramowicz, E. Gourgoulhon, T. Paumard, "Modelling the black hole silhouette in Sgr A* with ion tori", Astron. Astroph 543 (2012) A8
- ↑ «Physicists Detect Gravitational Waves, Proving Einstein Right». The New York Times. Consultado em 10 de março de 2020
- ↑ «Properties of the binary black hole merger GW150914». Physical Review Letters. 116. 241102 páginas. Bibcode:2016PhRvL.116x1102A. PMID 27367378. arXiv:1602.03840
 . doi:10.1103/PhysRevLett.116.241102
. doi:10.1103/PhysRevLett.116.241102
- ↑ «Is the gravitational-wave ringdown a probe of the event horizon?». Physical Review Letters. 116. 171101 páginas. 2016. Bibcode:2016PhRvL.116q1101C. PMID 27176511. arXiv:1602.07309
 . doi:10.1103/PhysRevLett.116.171101
. doi:10.1103/PhysRevLett.116.171101
- ↑ «Tests of general relativity with GW150914». LIGO
- ↑ «Astrophysical Implications of the Binary Black Hole Merger GW150914». Astrophys. J. Lett. 818 (2): L22. 2016. Bibcode:2016ApJ...818L..22A. arXiv:1602.03846
 . doi:10.3847/2041-8205/818/2/L22
. doi:10.3847/2041-8205/818/2/L22
- ↑ «Scientists Hear a Second Chirp From Colliding Black Holes». The New York Times
- ↑ «Monitoring Stellar Orbits around the Massive Black Hole in the Galactic Center». The Astrophysical Journal. 692: 1075–1109. Bibcode:2009ApJ...692.1075G. arXiv:0810.4674
 . doi:10.1088/0004-637X/692/2/1075
. doi:10.1088/0004-637X/692/2/1075
- ↑ «High Proper‐Motion Stars in the Vicinity of Sagittarius A*: Evidence for a Supermassive Black Hole at the Center of Our Galaxy». The Astrophysical Journal. 509: 678–686. Bibcode:1998ApJ...509..678G. arXiv:astro-ph/9807210
 . doi:10.1086/306528
. doi:10.1086/306528
- ↑ Broderick. «The Event Horizon of Sagittarius A*». The Astrophysical Journal. 701: 1357–1366. Bibcode:2009ApJ...701.1357B. arXiv:0903.1105
 . doi:10.1088/0004-637X/701/2/1357
. doi:10.1088/0004-637X/701/2/1357
- ↑ «NASA's NuSTAR Sees Rare Blurring of Black Hole Light». NASA
- ↑ «Researchers clarify dynamics of black hole rotational energy»
- ↑ Marck. «Short-cut method of solution of geodesic equations for Schwarzchild black hole». Classical and Quantum Gravity. 13: 393–402. Bibcode:1996CQGra..13..393M. ISSN 0264-9381. arXiv:gr-qc/9505010
 . doi:10.1088/0264-9381/13/3/007
. doi:10.1088/0264-9381/13/3/007
- ↑ a b c McClintock, J. E.; Remillard, R. A. (2006). «Black Hole Binaries». In: Lewin; van der Klis. Compact Stellar X-ray Sources. [S.l.: s.n.] Bibcode:2006csxs.book..157M. ISBN 978-0-521-82659-4. arXiv:astro-ph/0306213
 seção 4.1.5.
seção 4.1.5.
- ↑ «What powers a black hole's mighty jets?». Science | AAAS
- ↑ a b c d e f «Astrophysical evidence for the existence of black holes» (PDF). Classical and Quantum Gravity. 16: A3–A21. Bibcode:1999CQGra..16A...3C. arXiv:astro-ph/9912186
 . doi:10.1088/0264-9381/16/12A/301
. doi:10.1088/0264-9381/16/12A/301
- ↑ Winter. «XMM‐Newton Archival Study of the Ultraluminous X‐Ray Population in Nearby Galaxies». The Astrophysical Journal. 649: 730–752. Bibcode:2006ApJ...649..730W. arXiv:astro-ph/0512480
 . doi:10.1086/506579
. doi:10.1086/506579
- ↑ information@eso.org. «Hubble directly observes the disk around a black hole». www.spacetelescope.org -GB
- ↑ Muñoz. «A Study of Gravitational Lens Chromaticity with the Hubble Space Telescope». The Astrophysical Journal. 742. 67 páginas. Bibcode:2011ApJ...742...67M. arXiv:1107.5932
 . doi:10.1088/0004-637X/742/2/67
. doi:10.1088/0004-637X/742/2/67
- ↑ Bolton. «Identification of Cygnus X-1 with HDE 226868». Nature. 235: 271–273. Bibcode:1972Natur.235..271B. doi:10.1038/235271b0
- ↑ «Cygnus X-1 – a Spectroscopic Binary with a Heavy Companion ?». Nature. 235: 37–38. Bibcode:1972Natur.235...37W. doi:10.1038/235037a0
- ↑ Rolston, B. Universidade de Toronto, ed. «The First Black Hole». The bulletin. Consultado em 10 de março de 2020
- ↑ Shipman. «The implausible history of triple star models for Cygnus X-1 Evidence for a black hole». Astrophysical Letters. 16: 9–12. Bibcode:1975ApL....16....9S. doi:10.1016/S0304-8853(99)00384-4
- ↑ «Advection-dominated accretion and the black hole event horizon». New Astronomy Reviews. 51: 733–751. Bibcode:2008NewAR..51..733N. arXiv:0803.0322
 . doi:10.1016/j.newar.2008.03.002
. doi:10.1016/j.newar.2008.03.002
- ↑ «NASA scientists identify smallest known black hole» (Nota de imprensa). 1 de abril de 2008. Consultado em 10 de março de 2020
- ↑ a b Krolik, J. H. (1999). Active Galactic Nuclei. Princeton University Press. [S.l.: s.n.] ISBN 978-0-691-01151-6
- ↑ Sparke, L. S.; Gallagher, J. S. (2000). Galaxies in the Universe: An Introduction. Cambridge University Press. [S.l.: s.n.] ISBN 978-0-521-59740-1
- ↑ Kormendy. «Inward Bound – The Search For Supermassive Black Holes In Galactic Nuclei». Annual Review of Astronomy and Astrophysics. 33: 581–624. Bibcode:1995ARA&A..33..581K. doi:10.1146/annurev.aa.33.090195.003053
- ↑ King. «Black Holes, Galaxy Formation, and the MBH-σ Relation». The Astrophysical Journal Letters. 596: 27–29. Bibcode:2003ApJ...596L..27K. arXiv:astro-ph/0308342
 . doi:10.1086/379143
. doi:10.1086/379143
- ↑ Ferrarese. «A Fundamental Relation Between Supermassive Black Holes and their Host Galaxies». The Astrophysical Journal Letters. 539: 9–12. Bibcode:2000ApJ...539L...9F. arXiv:astro-ph/0006053
 . doi:10.1086/312838
. doi:10.1086/312838
- ↑ «RELEASE 15-001 – NASA's Chandra Detects Record-Breaking Outburst from Milky Way's Black Hole». NASA. Consultado em 12 de março de 2020
- ↑ «A Black Hole's Dinner is Fast Approaching». ESO Press Release. Consultado em 12 de março de 2020
- ↑ «Gravitational Lensing by Black Holes». General Relativity and Gravitation. 42: 2269–2300. Bibcode:2010GReGr..42.2269B. arXiv:0911.2187
 . doi:10.1007/s10714-010-0988-2
. doi:10.1007/s10714-010-0988-2
- ↑ «Can stellar mass black holes be quark stars?». Monthly Notices of the Royal Astronomical Society. 400: 1632–1642. Bibcode:2009MNRAS.400.1632K. arXiv:0908.2672
 . doi:10.1111/j.1365-2966.2009.15571.x
. doi:10.1111/j.1365-2966.2009.15571.x
- ↑ Alexander Kusenko. «Properties and signatures of supersymmetric Q-balls». arXiv:hep-ph/0612159

- ↑ «Preon stars: a new class of cosmic compact objects». Physics Letters B. 616: 1–7. Bibcode:2005PhLB..616....1H. arXiv:astro-ph/0410417
 . doi:10.1016/j.physletb.2005.04.034
. doi:10.1016/j.physletb.2005.04.034
- ↑ «Quantum gravity: general introduction and recent developments». Annalen der Physik. 15: 129–148. Bibcode:2006AnP...518..129K. arXiv:gr-qc/0508120
 . doi:10.1002/andp.200510175
. doi:10.1002/andp.200510175
- ↑ «The fuzzball proposal for black holes». Physics Reports. 467. Bibcode:2008PhR...467..117S. arXiv:0804.0552
 . doi:10.1016/j.physrep.2008.08.001
. doi:10.1016/j.physrep.2008.08.001
- ↑ «Black Hole Pretenders Could Really Be Bizarre Quantum Stars». Scientific American. Consultado em 12 de março de 2020
- ↑ «Black holes 'do not exist'». Nature News. doi:10.1038/news050328-8. Consultado em 12 de março de 2020
- ↑ Hawking. «Gravitational Radiation from Colliding Black Holes». Physical Review Letters. 26: 1344–1346. Bibcode:1971PhRvL..26.1344H. doi:10.1103/PhysRevLett.26.1344
- ↑ a b Wald. «The Thermodynamics of Black Holes». Living Reviews in Relativity. 4. Bibcode:2001LRR.....4....6W. PMC 5253844
 . PMID 28163633. arXiv:gr-qc/9912119
. PMID 28163633. arXiv:gr-qc/9912119 . doi:10.12942/lrr-2001-6
. doi:10.12942/lrr-2001-6
- ↑ 't Hooft, G. (2001). «The Holographic Principle». In: Zichichi. Basics and highlights in fundamental physics. Col: Subnuclear series. 37. [S.l.: s.n.] pp. 72–100. Bibcode:2001bhfp.conf...72T. ISBN 978-981-02-4536-8. arXiv:hep-th/0003004
 . doi:10.1142/9789812811585_0005
. doi:10.1142/9789812811585_0005
- ↑ «Microscopic origin of the Bekenstein-Hawking entropy». Physics Letters B. 379: 99–104. Bibcode:1996PhLB..379...99S. arXiv:hep-th/9601029
 . doi:10.1016/0370-2693(96)00345-0
. doi:10.1016/0370-2693(96)00345-0
- ↑ Carlip, S. (2009). «Black Hole Thermodynamics and Statistical Mechanics». Physics of Black Holes. Col: Lecture Notes in Physics. 769. [S.l.: s.n.] pp. 89–123. Bibcode:2009LNP...769...89C. ISBN 978-3-540-88459-0. arXiv:0807.4520
 . doi:10.1007/978-3-540-88460-6_3
. doi:10.1007/978-3-540-88460-6_3
- ↑ Hawking, S. W. «Does God Play Dice?». www.hawking.org.uk. Consultado em 10 de março de 2020. Cópia arquivada em 11 de janeiro de 2012
- ↑ The black hole information paradox. Bibcode:1995hep.th....8151G
- ↑ The information paradox: Conflicts and resolutions. Bibcode:2012Prama..79.1059M
- ↑ «Information in black hole radiation». Phys. Rev. Lett. 71: 3743–3746. Bibcode:1993PhRvL..71.3743P. PMID 10055062. arXiv:hep-th/9306083
 . doi:10.1103/PhysRevLett.71.3743
. doi:10.1103/PhysRevLett.71.3743
- ↑ «Average entropy of a subsystem». Phys. Rev. Lett. 71: 1291–1294. Bibcode:1993PhRvL..71.1291P. PMID 10055503. arXiv:gr-qc/9305007
 . doi:10.1103/PhysRevLett.71.1291
. doi:10.1103/PhysRevLett.71.1291
- ↑ «Astrophysics: Fire in the hole!». Nature. pp. 20–23. Bibcode:2013Natur.496...20M. doi:10.1038/496020a
- ↑ «Black Hole Firewalls Confound Theoretical Physicists». Scientific American Originally published Arquivado em 2014-06-03 no Wayback Machine
- ↑ «LIGO black hole echoes hint at general-relativity breakdown». Nature. 540. doi:10.1038/nature.2016.21135
Bibliografia[editar | editar código-fonte]
Leitura popular[editar | editar código-fonte]
- Ferguson, Kitty (1991). Black Holes in Space-Time. [S.l.]: Watts Franklin. ISBN 978-0-531-12524-3
- Hawking, Stephen (1988). A Brief History of Time. [S.l.]: Bantam Books, Inc. ISBN 978-0-553-38016-3
- Hawking, Stephen; Penrose, Roger (1996). The Nature of Space and Time. [S.l.]: Princeton University Press. ISBN 978-0-691-03791-2
- Melia, Fulvio (2003). The Black Hole at the Center of Our Galaxy. [S.l.]: Princeton U Press. ISBN 978-0-691-09505-9
- Melia, Fulvio (2003). The Edge of Infinity. Supermassive Black Holes in the Universe. [S.l.]: Cambridge U Press. ISBN 978-0-521-81405-8
- Pickover, Clifford (1998). Black Holes: A Traveler's Guide. [S.l.]: Wiley, John & Sons, Inc. ISBN 978-0-471-19704-1
- Thorne, Kip S. (1994). Black Holes and Time Warps. [S.l.]: Norton, W. W. & Company, Inc. ISBN 978-0-393-31276-8
- Susskind, Leonard (2008). The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics. [S.l.]: Little, Brown and Company. ISBN 978-0316016407
- Wheeler, J. Craig (2007). Cosmic Catastrophes 2nd ed. [S.l.]: Cambridge University Press. ISBN 978-0-521-85714-7
Livros didáticos e monografias universitárias[editar | editar código-fonte]
- Carroll, Sean M. (2004). Spacetime and Geometry. [S.l.]: Addison Wesley. ISBN 978-0-8053-8732-2, the lecture notes on which the book was based are available for free from Sean Carroll's website.
- Carter, B. (1973). «Black hole equilibrium states». In: DeWitt, B. S.; DeWitt, C. Black Holes. [S.l.: s.n.]
- Chandrasekhar, Subrahmanyan (1999). Mathematical Theory of Black Holes. [S.l.]: Oxford University Press. ISBN 978-0-19-850370-5
- Frolov, V. P.; Novikov, I. D. (1998). «Black hole physics»
- Frolov, Valeri P.; Zelnikov, Andrei (2011). Introduction to Black Hole Physics. Oxford: Oxford University Press. ISBN 978-0-19-969229-3. Zbl 1234.83001
- Hawking, S. W.; Ellis, G. F. R. (1973). Large Scale Structure of space time. [S.l.]: Cambridge University Press. ISBN 978-0-521-09906-6
- Melia, Fulvio (2007). The Galactic Supermassive Black Hole. [S.l.]: Princeton U Press. ISBN 978-0-691-13129-0
- Misner, Charles; Thorne, Kip S.; Wheeler, John (1973). Gravitation. [S.l.]: W. H. Freeman and Company. ISBN 978-0-7167-0344-0
- Taylor, Edwin F.; Wheeler, John Archibald (2000). Exploring Black Holes. [S.l.]: Addison Wesley Longman. ISBN 978-0-201-38423-9
- Wald, Robert M. (1984). General Relativity. [S.l.]: University of Chicago Press. ISBN 978-0-226-87033-5
- Wald, Robert M. (1992). Space, Time, and Gravity: The Theory of the Big Bang and Black Holes. [S.l.]: University of Chicago Press. ISBN 978-0-226-87029-8
- Price, Richard; Creighton, Teviet (2008). «Black holes». Scholarpedia. 3 (1). 4277 páginas. Bibcode:2008SchpJ...3.4277C. doi:10.4249/scholarpedia.4277
Artigos de revisão
- Gallo, Elena; Marolf, Donald (2009). «Resource Letter BH-2: Black Holes». American Journal of Physics. 77 (4): 294–307. Bibcode:2009AmJPh..77..294G. arXiv:0806.2316
 . doi:10.1119/1.3056569
. doi:10.1119/1.3056569 - Hughes, Scott A. (2005). «Trust but verify: The case for astrophysical black holes». arXiv:hep-ph/0511217
 Lecture notes from 2005 SLAC Summer Institute.
Lecture notes from 2005 SLAC Summer Institute.
Ligações externas[editar | editar código-fonte]
- Enciclopédia Stanford de Filosofia : " Singularidades e Buracos Negros ", de Erik Curiel e Peter Bokulich.
- Buracos negros: atração implacável da gravidade - Site multimídia interativo sobre física e astronomia dos buracos negros do Instituto de Ciências do Telescópio Espacial
- Visualização de um buraco negro pela ESA