Lei de Gauss
A lei de Gauss é a lei que estabelece a relação entre o fluxo do campo elétrico através de uma superfície fechada com a carga elétrica que existe dentro do volume limitado por esta superfície. A lei de Gauss é uma das quatro equações de Maxwell, juntamente com a lei de Gauss do magnetismo, a lei da indução de Faraday e a lei de Ampère-Maxwell. Foi elaborada por Carl Friedrich Gauss em 1835, porém só foi publicada após 1867.[1] Gauss foi um matemático alemão que fez contribuições importantes para a teoria dos números, a geometria e a probabilidade, tendo também contribuições em astronomia e na medição do tamanho e do formato da Terra.[2]
Fluxo do campo elétrico[editar | editar código-fonte]

O fluxo de campo elétrico, , é uma grandeza escalar e pode ser considerado como uma medida do número de linhas de campo que atravessam a superfície.[2][3] Convenciona-se que se há mais linhas de campo saindo da superfície do que entrando, o fluxo do campo elétrico através da superfície é positivo e se há mais linhas de campo entrando na superfície do que saindo da mesma, o fluxo é negativo. Além disso, é importante observar o fato de que se o número de linhas de campo que entra na superfície é igual ao número de linhas de campo que sai da superfície, então o fluxo de campo elétrico através da superfície é nulo.[2][4]
Para obter o fluxo do campo elétrico E através de uma superfície fechada em que E é não-uniforme, é preciso dividi-la em elementos de área infinitesimal dA. Define-se, então, um vetor dA cujo módulo é dA, a direção é perpendicular ao elemento de área e o sentido é adotado como o sentido da normal ao elemento infinitesimal saindo da superfície. Assim, esses elementos infinitesimais são tão pequenos que E pode ser considerado constante em todos os pontos de um mesmo elemento de área.[2] Portanto, podemos definir o fluxo de E através de uma superfície S da seguinte forma:
ou, no caso de uma superfície fechada:
Da definição de produto escalar, tem-se que: E . dA = |E||dA| cosθ = |E|cosθ |dA|. Como θ é o ângulo entre os vetores E e dA, |E|cosθ é a projeção do vetor E sobre o vetor dA, logo a função desse produto escalar dentro da integral é selecionar algo proporcional à componente do campo elétrico que está "furando" à superfície infinitesimal dA, o que é coerente com a definição de fluxo dada anteriormente.
Por fim, se uma carga pontual estiver fora da superfície, as linhas de campo que partem da carga pontual irão entrar e sair da superfície, visto que as linhas de campo de uma carga pontual são radiais. Por isso, pode-se concluir que se uma carga está fora de uma superfície, então o fluxo do campo elétrico dessa carga através da superfície é nulo, ou seja:
, se estiver externa à superfície.

Lei de Gauss[editar | editar código-fonte]
A lei de Gauss estabelece uma relação entre o fluxo de campo elétrico através de uma superfície fechada e as cargas que estão no interior dessa superfície. Algumas considerações importantes sobre a de lei de Gauss são:
- A lei de Gauss não contém nenhuma informação que não esteja contida na lei de Coulomb e no princípio da superposição. Inclusive, é possível obter a lei de Coulomb a partir da lei de Gauss e vice-versa.[3]
- É fundamental para a lei de Gauss, o fato de que a força elétrica é proporcional ao inverso do quadrado da distância. É esse fato que faz com que o fluxo de E não dependa da "superfície gaussiana" escolhida e dependa apenas das cargas que estão localizadas no interior da superfície. Dessa forma, é possível pensar numa lei de Gauss que estabeleça uma relação de fluxo para qualquer campo cuja lei de força associada a esse campo seja proporcional ao inverso do quadrado da distância, como a força gravitacional, por exemplo, logo existe uma lei de Gauss da gravitação.[3]
- Apesar da lei de Coulomb nos fornecer o necessário para calcular o campo elétrico de uma distribuição de cargas, muitas vezes, as integrais que envolvem o cálculo do campo elétrico podem ser complicadas de serem resolvidas, mesmo para casos razoavelmente simples. É nesse ponto que reside um dos aspectos de maior eficiência da lei de Gauss: o cálculo do campo elétrico em distribuições de carga que possuam determinados tipos de simetria torna-se extremamente simples.[3]
- A lei de Gauss se refere sempre ao fluxo no interior de uma superfície gaussiana escolhida. Portanto, para utilizar a lei de Gauss, é necessário definir o que é uma "superfície gaussiana". Esta é, por sua vez, uma superfície arbitrariamente escolhida. Normalmente, essa superfície é escolhida de modo que a simetria da distribuição de carga permita, ao menos em parte da superfície, um campo elétrico de intensidade constante.[2]
Forma integral da lei de Gauss[editar | editar código-fonte]

Para entender como a lei de Gauss relaciona o fluxo do campo elétrico no interior de uma superfície gaussiana com a carga no interior dessa mesma superfície, escolhe-se uma superfície qualquer com uma carga q em seu interior. Então, escolhe-se outra superfície gaussiana S' que está envolvendo q no interior de S. A forma dessa superfície S' pode ser qualquer, contudo, a fim de facilitar os cálculos e a visualização, vamos fazer dessa superfície S', uma esfera de raio r centrada na carga q. O raio r é tal que S' esteja inteiramente dentro de S.[4] O fluxo do campo elétrico através dessa esfera é dado por:
Como tanto E quanto dA são radiais, o produto escalar torna-se o produto dos módulos, então:
Como |E| é constante na superfície da esfera, podemos tirá-lo da integral e temos:
Portanto, é possível observar que o fluxo através da superfície S' é um número que independe do raio da esfera. Dessa forma, o fluxo que sai da superfície S também será . Esse é um valor independente da forma da superfície S, desde que esta tenha uma carga q em seu interior. Se uma carga q está no exterior da superfície S, as suas linhas de campo entram e saem da superfície S, por isso, o fluxo de campo elétrico dessa carga sobre a superfície é nulo. Logo:
Por fim, se tivermos mais de uma carga no interior da superfície gaussiana, vale o princípio da superposição de modo que:
Portanto, a Lei de Gauss na forma integral pode ser enunciada da seguinte forma:
Forma diferencial da lei de Gauss[editar | editar código-fonte]
Demonstração Pelo teorema da divergência:[3][5] Pode-se reescrever a carga interna à superfície, qint, em termos da densidade ρ:
Desse modo, usando o teorema de Stokes,a lei de Gauss, assume a forma:
Por fim, como se quer que essa igualdade valha para qualquer volume, os integrandos devem ser iguais, logo:
Relação entre a lei de Gauss e a lei de Coulomb[editar | editar código-fonte]
Demonstração Existe uma relação entre a lei de Gauss e a lei de Coulomb, de forma que nenhuma das duas leis é mais fundamental do que a outra. Partindo-se de uma delas pode-se obter a outra como consequência. Partindo-se da lei de Coulomb, tem-se que[3]:
onde Ω significa que a integral ocorre em todo o espaço e , isto é, é um vetor que vai da origem até um elemento infinitesimal de volume da distribuição de carga geradora do campo, r é um vetor que vai da origem ao ponto no qual se deseja calcular calcular o campo e é o vetor que representa a distância entre o elemento infinitesimal da fonte de campo elétrico e o ponto no qual se deseja calcular o campo. Pode-se reescrever a equação acima em termos da densidade volumétrica de carga da seguinte forma:
onde dτ' é um elemento infinitesimal de volume da distribuição de carga geradora do campo. Sabe-se que, pelo teorema da divergência, o fluxo do campo elétrico pode ser escrito do seguinte modo:
Calculando-se o divergente de E, obtém-se:
Entretanto:
Esse é um resultado importante e muito usado em eletrostática. Um cálculo de divergente acima de forma não muito atenta pode levar, equivocadamente, a um divergente nulo. Em contrapartida, pode-se obter esse resultado resolvendo a integral de superfície de numa superfície esférica de raio R, que leva ao resultado: . Portanto, isso sugere que o divergente deve ser calculado de forma mais cuidadosa, introduzindo o conceito da distribuição delta de Dirac em eletrostática. Sabendo, então, que : e usando o conceito de distribuição delta de Dirac:
Chega-se, portanto na lei de Gauss na forma diferencial. Pode-se obter a lei de Gauss na forma integral do seguinte modo:
Tomando uma superfície esférica S, de raio r, centrada na carga q, e partindo-se da lei de Gauss, tem-se que:[2]
Como escolheu-se uma carga positiva, pode-se observar que, por simetria, o campo na superfícies esférica é radial e aponta para fora da esfera, visto que as linhas de campo divergem de uma carga positiva. Portanto, E e dA apontam na mesma direção e sentido de modo que:
Como E possui a mesma intensidade para todos os pontos da superfície esférica, pode-se retirá-lo de dentro do símbolo de integração:
Mas, a área da superfície esférica é 4πr², logo:
Contudo, já foi considerado antes que o campo deve estar na direção radial, então:
Aplicações[editar | editar código-fonte]
É importante ressaltar que a lei de Gauss se torna eficiente apenas em casos em que há simetria. Mais precisamente, nos casos nos quais existe simetria esférica, cilíndrica ou plana.[3] Dessa forma, construir superfícies gaussianas que aproveitem a simetria é de vital importância para a aplicação da lei de Gauss,[2] visto que a eficiência da lei de Gauss consiste em utilizar a simetria das distribuições de carga para calcular campo elétrico dessas com mais facilidade.[2][3]
Campo elétrico no interior e no exterior de uma esfera[editar | editar código-fonte]

Para uma esfera de raio R com carga Q uniformemente distribuída pela esfera, tem-se:
- No exterior da esfera
Para se obter o campo no exterior da esfera, escolhe-se, como superfície gaussiana, a superfície esférica de raio r', situada no exterior da esfera de raio R. Pode-se imaginar que, muito longe da esfera, o campo elétrico que se sente é como o campo de uma carga puntiforme. Além disso, devido à simetria esférica, o campo elétrico deve apontar na direção radial. Dessa forma, aplicando a lei de Gauss:
O campo deve apontar na direção radial e, portanto, E e dA possuem a mesma direção e sentido e, por isso, segue que: E . dA = E dA. Logo:
O módulo do campo elétrico na superfície gaussiana é constante, visto que, nesse caso, o campo deve depender da distância em relação à esfera e, portanto, E pode sair da Integral.
Logo:
- No interior da esfera
Para como o campo elétrico varia no interior da esfera, deve-se tomar como superfície gaussiana a superfície esférica de raio r no interior da esfera de raio R. Nesse caso, como a carga está uniformemente distribuída pela esfera, a densidade volumétrica de carga, ρ, é a mesma em todos os pontos da esfera,então pode-se observar que:
onde Vg é o volume da superfície gaussiana escolhida.
Dessa forma:
Os mesmos argumentos dados anteriormente para que o produto escalar E . dA seja E dA e para que E saia da integral continuam sendo válidos, logo:
Logo:
Portanto, no caso de uma esfera uniformemente carregada:
Campo elétrico no interior e no exterior de uma casca esférica[editar | editar código-fonte]
Para se resolver esse problema, utiliza-se a figura 4 novamente, porém com uma ligeira diferença: o interior da esfera de raio R é "oco", isto é, tem-se apenas uma casca esférica com carga Q uniformemente distribuída sobre sua superfície.
- No exterior da esfera
Escolhendo a superfície de raio r' como mostrada na figura 4, tem-se, pela lei de Gauss, o mesmo resultado que foi obtido para o campo no exterior de uma esfera. A carga interna à superfície gaussiana, qint, é Q nesse caso, como no caso anterior da esfera uniformemente carregada, de forma que o cálculo para o campo elétrico exterior à da casca esférica se desenvolve da mesma forma que o cálculo para o campo no exterior à esfera uniformemente carregada, então:
- No interior da casca esférica
Escolhendo a superfície gaussiana de raio r, no interior da casca esférica, tem-se:
Portanto:
Logo:
Portanto, no caso de uma casca esférica uniformemente carregada:
Campo elétrico de um plano infinito[editar | editar código-fonte]
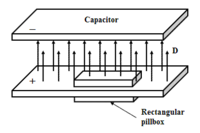
Supõe-se um plano infinito com densidade de carga σ e se deseja calcular o campo elétrico produzido por esse plano. Apesar de o problema ser bem diferente do apresentado na figura 5, visto que, no problema em questão, está-se estudando um plano infinito e não o campo no interior de um capacitor, é interessante utilizar uma superfície gaussiana de mesma forma que a superfície retratada na placa de baixo do capacitor da figura 5. Utilizando, portanto, a superfície de um paralelepípedo cortando o plano infinito como superfície S, tem-se:
Por simetria, o campo elétrico deve apontar para "fora" do plano, isto é, ele aponta na direção para pontos acima do plano e na direção para pontos abaixo do plano. Dessa forma, as únicas superfícies superior e inferior da superfície do paralelepípedo é que serão "furadas" pelo campo elétrico, por isso:
onde A é a área da superfície superior e inferior da superfície do paralelepípedo. Sabe-se, também, que : σ = qint/A, logo : qint = σA, portanto:
ou
onde é um vetor unitário que aponta para fora da superfície do plano.

Campo elétrico de uma carga uniformemente distribuída ao longo de um fio extenso[editar | editar código-fonte]
Vamos considerar um fio longo que possui uma densidade linear uniforme de cargas positiva em toda sua extensão. Podemos determinar o campo elétrico produzido por esta distribuição de cargas através da Lei de Gauss. Para tal, devido à simetria cilíndrica existente, vamos escolher como superfície gaussiana uma superfície cilíndrica de raio e comprimento , coaxial com o fio, como mostrado na Figura 6. Como o fio possui uma densidade linear de cargas uniforme, podemos relacionar a carga contida no interior da superfície gaussiana com esta densidade pela seguinte expressão: . Dessa forma, a Lei de Gauss pode ser escrita como[2]:
Uma vez que o fio está carregado positivamente e considerando sua simetria cilíndrica, esperamos que o campo elétrico produzido por ele aponte radialmente para fora do fio. Tal característica faz com que o fluxo de campo elétrico seja nulo nos planos da base da superfície gaussiana, isto é, , já que o ângulo entre e é . Na superfície lateral, o diferencial de fluxo passa a ser escrito como , já que o ângulo entre e é . Dessa forma, sendo a área lateral da superfície gaussiana, temos que (onde SL significa Superfície Lateral):
Logo, a expressão vetorial da distribuição espacial do campo elétrico resulta em:
Lei de Gauss para dielétricos[editar | editar código-fonte]

Cargas livres e cargas ligadas[editar | editar código-fonte]
Um dielétrico em presença de um campo elétrico, sofre o que se chama de polarização. A polarização consiste na separação das cargas positivas e negativas desse dielétrico, visto que o campo elétrico acelera cargas positivas no sentido do campo e cargas negativas no sentido oposto. Essas cargas geradas por esse efeito de polarização é o que se chama de cargas ligadas. O material passa a ser constituído de dipolos, como mostrado na figura 6. Dessa forma, as cargas estão "presas" aos dipolos, não estão livres para se mover. Por sua vez, é chamado de carga livre, o restante das cargas, que não foram geradas por esse efeito de polarização. As cargas livres são as cargas com as quais se está mais habituado quando se estuda eletrostática.[3] Desse modo, num dielétrico, a densidade volumétrica de carga pode ser escrita como:
onde é a densidade volumétrica de carga ligada e é a densidade volumétrica de carga livre.
Demonstração da lei de Gauss para dielétricos[editar | editar código-fonte]
Demonstração Pela lei de Gauss na forma diferencial:
onde usamos o resultado de que (ver Leitura Complementar(**)) e P é o vetor polarização, que é definido como o momento de dipolo por unidade de volume.
A expressão entre parênteses é designada pela letra D, que é o chamado vetor de deslocamento elétrico. Ou seja:
Portanto:
Essa é a lei de Gauss em dielétricos na forma diferencial. Para obter a forma integral:
Pelo teorema de Stokes:
Pode-se observar que a lei de Gauss para dielétricos só faz referência à cargas livres, que é o tipo de carga sobre o qual se tem controle e se tem mais facilidade de medir, por isso, a lei de Gauss para dielétricos torna-se um artifício muito útil para calcular o vetor deslocamento elétrico de diferentes distribuições de carga e, consequentemente, o campo elétrico dessas distribuições, que pode ser obtido através da relação entre E e D.
Referências
- ↑ Bellone, Enrico (1980). A World on Paper: Studies on the Second Scientific Revolution. [S.l.: s.n.]
- ↑ a b c d e f g h i Halliday, D., Resnick, R., Krane, K. Física 3, 5a ed. GEN|LTC (2010).
- ↑ a b c d e f g h i Griffiths, D. J. Introduction to Electrodynamics, 3a ed. New Jersey: Prentice Hall (1999).
- ↑ a b Feynman, R. P., Leighton, R. B., Sands M. The Feynman Lectures on Physics,vol 2. 2a ed. Bookman (2008).
- ↑ Jackson J. D. Classical Eletrodynamics, 2a ed. John Sons and wiley (1975).


























































































