Corpo negro

Na Física, um corpo negro é um objeto hipotético que absorve toda a radiação eletromagnética que nele incide: nenhuma luz o atravessa e nem é refletida. Um corpo com essa propriedade, em princípio, não poderia ser visto, daí o seu nome.[1] Apesar disso, corpos negros emitem radiação, o que permite determinar sua temperatura. Em equilíbrio termodinâmico, um corpo negro ideal irradia energia na mesma taxa que a absorve,[1] sendo essa uma das propriedades que o tornam uma fonte ideal de radiação térmica.[2] Na natureza não existem corpos negros perfeitos, já que nenhum objeto consegue ter absorção e emissão perfeitas.
Podemos imaginar uma caixa opaca, com um pequeno buraco. Uma radiação incidente sobre o buraco é refletida seguidamente pelas paredes internas e dificilmente conseguirá sair pelo buraco da caixa mas se aumentássemos a temperatura no interior dessa caixa uma quantidade de radiação sairia pelo buraco, o que demonstra que o corpo negro ao ser aquecido emite luz. Com essa ideia podemos comparar essa caixa opaca a um corpo negro ideal.[3]
Independente da sua composição, verifica-se que todos os corpos negros à mesma temperatura T emitem radiação térmica com mesmo espectro. Do mesmo modo, todos os corpos, com temperatura acima do zero absoluto, emitem radiação térmica. Conforme a temperatura da fonte luminosa aumenta, o espectro de corpo negro apresenta picos de emissão em menores comprimentos de onda, partindo das ondas de rádio, passando pelas micro-ondas, infravermelho, luz visível, ultravioleta, raios X e radiação gama. Em temperatura ambiente (cerca de 300 K), corpos negros emitem na região do infravermelho do espectro. À medida que a temperatura aumenta algumas centenas de kelvins, corpos negros começam a emitir radiação em comprimentos de onda visíveis ao olho humano (compreendidos entre 380 a 780 nanômetros). A cor com maior comprimento de onda é o vermelho, e as cores seguem como no arco-íris, até o violeta, que tem o menor comprimento de onda do espectro visível.
Um bom modelo de corpo negro são as estrelas, como o Sol, no qual a radiação produzida em seu interior é expelida para o universo e consequentemente aquece o nosso planeta. A cor branca do Sol corresponde a uma temperatura superficial da ordem de 5 750 K.[4][5][6]
A primeira menção a corpos negros deve-se a Gustav Kirchhoff em 1860, em seu estudo sobre a espectrografia dos gases. Muitos estudiosos tentaram conciliar o conceito de corpo negro com a distribuição de energia prevista pela termodinâmica, mas os espectros obtidos experimentalmente, ainda que válidos para baixas frequências, mostravam-se muito discrepantes da previsão teórica, explicitada pela Lei de Rayleigh-Jeans para a radiação de corpo negro. Uma boa aproximação dos valores para o máximo de emissão para cada temperatura era dado pela Lei de Wien, porém foi Max Planck que, em 1901, ao introduzir a Constante de Planck, como mero recurso matemático, determinou a quantização da energia, o que mais tarde levou à teoria quântica que, por sua vez, rumou para o estudo e surgimento da mecânica quântica.[7][8]
Baseada no física clássica, o modelo de Rayleigh-Jeans, que comparado com medidas experimentais possuía resultados aceitáveis para baixas frequências, mas o modelo previa que conforme a temperatura aumentasse a frequência deveria aumentar proporcionalmente, tendendo ao infinito, o que apresentou uma grande incompatibilidade com os resultados experimentais, que diziam que conforme aumentasse a temperatura do corpo, a frequência deveria atingir um pico e em seguida diminuir.
Isso porque, o modelo de Rayleigh-jeans não levava em consideração a conservação de energia, isso explica porque em seu modelo um corpo negro emitiria quantidade letal de radiação apenas por existir e estar a uma temperatura maior que a ambiente. Esse problema ficou conhecido como a Catástrofe do ultravioleta.
Durante muitos anos a física não apresentava uma solução para esse problema, até que Marx Planck (1900), começou seus estudos sobre o corpo negro, antes de Planck, os átomos que compunham os corpos negros poderiam ser vistos como pequenas molas que oscilavam a uma determinada frequência, por qualquer quantidade mínima de energia.
O postulado de Planck afirmava que os corpos negros continuavam sendo formados com osciladores, que absorvem radiação e depois oscilavam com determinada energia, energia essa que obedecendo a Lei de Conservação de Energia, deveria ser a mesma que da radiação emitida. Neste momento os únicos valores de energia possíveis seriam múltiplos inteiros de um número pequeno, que futuramente ficou conhecido como a quantização de energia.[9]
Explicação[editar | editar código-fonte]
Experimentalmente, a radiação mais próxima a de um corpo negro ideal é aquela emitida por pequenas aberturas de extensas cavidades. Qualquer luz entrando pela abertura deve ser refletida várias vezes nas paredes da cavidade antes de escapar e, então, a probabilidade de que seja absorvida pelas paredes durante o processo é muito alta, independente de qual seja o material que a compõe ou o comprimento de onda da radiação. Tal cavidade então é uma aproximação de um corpo negro e, ao ser aquecida, o espectro da radiação do buraco (a quantidade de luz emitida do buraco em cada comprimento de onda) é contínuo, e não depende do material da cavidade (compare com espectro de emissão). Por um teorema provado por Kirchhoff, o espectro observado depende apenas da temperatura das paredes da cavidade. A Lei de Kirchhoff nos diz que num corpo negro ideal, em equilíbrio termodinâmico a temperatura T, a radiação total emitida deve ser igual à radiação total absorvida.
Calcular a curva formada pelo espectro de radiação emitido por um Corpo Negro foi um dos maiores desafios no campo da Física Teórica durante o fim do século XIX. O problema finalmente foi resolvido em 1901 por Max Planck com a Lei de Planck da Radiação de Corpo Negro. Fazendo mudanças na Lei da Radiação de Wien consistentes com a termodinâmica e o eletromagnetismo, ele achou uma fórmula matemática que descrevia os dados experimentais de maneira satisfatória. Para achar uma interpretação física, Planck, então, assumiu que a energia das oscilações na cavidade são quantificadas. Einstein trabalhou em cima desta ideia e propôs a quantificação da radiação eletromagnética em 1905 para explicar o efeito fotoelétrico. Estes avanços teóricos resultaram na substituição do eletromagnetismo clássico pelos quanta (plural de quantum) eletrodinâmicos. Hoje, estes quanta são chamados fótons. Também, isso levou ao desenvolvimento de versões quânticas para a mecânica estatística, chamada estatística de Fermi-Dirac e estatística de Bose-Einstein, cada uma aplicável a classes diferentes de partículas.
O comprimento de onda na qual a radiação é máxima é dada pela Lei de Wien e a potência total emitida por unidade de área é dada pela Lei de Stefan-Boltzmann. Então, a temperatura aumenta, a cor muda de vermelho para amarelo para branco para azul. Mesmo que o pico do comprimento de onda mova-se para o ultravioleta, a radiação continua sendo emitida no comprimento de onda do azul.
A luminosidade ou intensidade observada não é função da direção. Então, um corpo negro é um irradiador de Lambert ideal.
Objetos reais nunca se comportam como corpos negros ideais. A radiação emitida é uma fração do que a emissão ideal deveria ser. A emissividade de um material especifica o quão bem um corpo irradia energia em comparação a um corpo negro. Esta emissividade depende de fatores como temperatura, ângulo de emissão e o comprimento de onda. De qualquer maneira, é comum na engenharia assumir que a emissividade espectral de uma superfície não depende do comprimento de onda, então a emissividade é uma constante. Isso é conhecido como corpo cinza.
Lei de Stefan ou Lei de Stefan-Boltzmann[editar | editar código-fonte]
Nos seus estudos da radiação de corpo negro Joseph Stefan chegou a seguinte função:[10]
Onde:
- = Área de emissão do corpo negro;
- = Potência total irradiada (W);
- = — também chamada de constante de Stefan;
- = Temperatura (K).
Esta expressão mostra que a potência irradiada por unidade de área varia apenas com a temperatura, ela não depende do material de sua cor entre outras características do corpo. O valor de R também indica a rapidez com a qual o corpo emite energia, por exemplo se a temperatura for triplicada a energia emitida será aumentada () vezes ou se for quadruplicada a nova emissão será aumentada () vezes. Corpos reais irradiam menos energia por unidade de área que o corpo negro, para calcular a energia irradiada por esses corpos é necessária a inclusão de um parâmetro denominado emissividade ε, a emissividade depende das características do material (cor, composição de sua superfície), seu valor fica entre zero e um.
Experimento de Lummer e Pringsheim[editar | editar código-fonte]
Em 1899, O. Lummer e E. Pringsheim conduziram uma medição da distribuição R(λ, T) de um corpo negro. O método experimental desenvolvido para determinar essa distribuição consiste no procedimento: um feixe de radiação térmica seguinte de uma pequena abertura encontrado de uma cavidade é direcionado para uma rede de difração, cuja projeção da distribuição é captada por uma tela. Nessa tela, os comprimentos de onda são separados através das características ópticas da difração. Um detector é movido verticalmente ao longo da tela para medir a potência R(λ, T)dλ emitida em intervalos de comprimento de onda λ e λ + dλ. Os valores resultantes de R(λ, T) são então representados em função de λ para diferentes temperaturas T. [11]
Lei de deslocamento de Wien[editar | editar código-fonte]

A emissão de radiação do corpo negro apresenta uma distribuição espectral que depende apenas da temperatura . Seja a potência emitida por unidade de área compreendida entre e . A figura 2 mostra valores da distribuição espectral em função de para muitos valores de entre 3 500 K e 5 500 K.
Foi Wien quem pela primeira vez observou que o comprimento de onda máximo emitido era inversamente proporcional a temperatura do corpo negro e escreveu a equação que recebeu seu nome.[10]
- .
Onde
- = Comprimento de onda para o qual a emissão por unidade de área é máxima (m).
- = Temperatura do corpo negro (K).
Teoria de Planck da radiação de corpo negro[editar | editar código-fonte]
Ao tentar solucionar a discrepância entre a teoria e a experiência, Planck foi levado a considerar a hipótese de uma violação da lei da equipartição da energia sobre o qual a teoria se baseava. Planck supôs que a energia poderia ter apenas certos valores discretos, em vez de qualquer valor, e que os valores discretos fossem uniformemente distribuídos. Isto é, tomou
como o conjunto de valores possíveis da energia. Aqui é o intervalo constante entre valores possíveis sucessivos da energia. Planck supôs também que as energias sucessivas e a frequência da radiação emitida fossem grandezas proporcionais, portanto,
Escrito na forma de uma equação em vez de uma proporcionalidade, temos
onde é a constante de proporcionalidade.
Cálculos posteriores permitiram a Planck determinar o valor da constante , obtendo o valor que ajustava melhor sua teoria aos dados experimentais. O valor obtido por ele estava bem próximo do valor atualmente aceito
Esta constante, muito famosa e corrente na mecânica quântica, é chamada constante de Planck.
A fórmula obtida o permitiu calcular o espectro de corpo negro em total acordo com os resultados experimentais.
Postulado de Planck[editar | editar código-fonte]
A contribuição de Planck pode ser colocada na forma do seguinte postulado:
Qualquer ente físico com um grau de liberdade cuja "coordenada" é uma função senoidal do tempo (isto é, executa oscilações harmônicas simples) pode possuir apenas energias totais que satisfaçam a relação onde é a frequência da oscilação, uma constante universal e só pode assumir valores inteiros.
A energia do ente que obedece ao postulado de Planck é dita quantizada, os estados de energia possíveis são ditos estados quantizados, e o é dito número quântico.[11]
Implicações[editar | editar código-fonte]
A ideia de que a energia é quantizada apesar de parecer apenas um truque matemático para explicar os resultados experimentais da radiação de corpo negro, foi fundamental para o desenvolvimento de um dos pilares da física moderna, a mecânica quântica.[12]
Exemplos de emissão de corpo negro[editar | editar código-fonte]
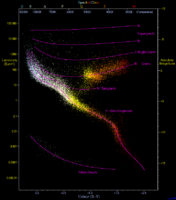
As diferentes cores das estrelas são um bom exemplo de corpos com espectros semelhantes ao de um corpo negro. As estrelas mais avermelhadas, como Antares e Betelgeuse, classificadas como tipo M no Diagrama de Hertzsprung-Russell, têm as menores temperaturas superficiais, enquanto as estrelas mais azuladas, como Rigel e Sirius, com classificação O ou B no diagrama H-R, têm temperaturas superficiais bem maiores.
Os materiais que, quando aquecidos, tornam-se incandescentes, também são bons exemplos de como a temperatura de um corpo interfere na sua emissão. Filamentos de lâmpadas incandescentes e uma barra de ferro aquecida são objetos presentes no cotidiano que emitem radiação com espectro próximo ao de um corpo negro.
Referências
- ↑ a b Oliveira, Kepler; Saraiva, Maria de Fátima (2004). Astronomia e Astrofísica. São Paulo: Livraria da Física. ISBN 85-88325-23-3
- ↑ Eisberg, Robert; Resnick, Robert (1979). Física Quântica. [S.l.]: Elsevier. ISBN 85-700-1309-4
- ↑ 1 Kittel, 2 Kroemer, 1 Charles, 2 Herbert (1980). Thermal Physics. San Francisco: W.H. Freeman and Company
- ↑ «Why is the Sky Blue?». Science Made Simple
- ↑ Picazio, E., (ed.) (2011). O Céu que nos Envolve. [S.l.]: Odysseus. ISBN 978-85-7876-021-2
- ↑ «Radiação dos Corpos Negros». Consultado em 25 de novembro de 2012
- ↑ Caruso, Francisco; Oguri, Vitor (2006). Física Moderna. página 299 em diante. [S.l.]: Elsevier. ISBN 85-352-1878-5
- ↑ Física UFPR. Acessada em 04 de dezembro de 2012.
- ↑ Planck, Marx. THE THEORY OF HEAT RADIATION. New York: Dover publications
- ↑ a b Tipler e Llewellyn, Paul A. e Ralph A. (2006). Física Moderna. [S.l.]: LTC. ISBN 978-85-216-1274-2
- ↑ a b Resnick, Eisberg (1979). Física Quântica. Rio de Janeiro: Elsevier. pp. 19–42
- ↑ SEGRÈ, Emilio (1987). Dos Raios X aos Quarks: Físicos Modernos e suas Descobertas. Brasília: Editora Universidade de Brasília. pp. 36, Fig. 4.4



























