Geometria do táxi
Este artigo contém uma lista de referências no fim do texto, mas as suas fontes não são claras porque não são citadas no corpo do artigo, o que compromete a confiabilidade das informações. (Outubro de 2023) |

A Geometria do táxi, considerada por Hermann Minkowski no século XIX, é uma forma de geometria em que a usual métrica da geometria euclidiana é substituída por uma nova métrica em que a distância entre dois pontos é a soma das diferenças absolutas de suas coordenadas. A métrica do táxi é também conhecida como distância L1, ou distância de Manhattan, com variações correspondentes no nome da geometria. O último nome faz alusão ao formato quadriculado da maior parte das ruas na ilha de Manhattan. Tal configuração faz com que a menor distância a ser percorrida por um carro que vai de um ponto a outro na cidade tenha como valor aquele número fornecido pela métrica L1.
A distância de Manhattan é comumente utilizada em desenvolvimento de jogos como uma heurística para o Algoritmo A*.[1]
Descrição formal[editar | editar código-fonte]
A taxi-distância entre dois pontos em um espaço euclidiano com sistema de coordenadas cartesianas fixado é a soma dos comprimentos das projeções do segmento de reta que liga os pontos sobre os eixos coordenados. Por exemplo, no plano, a taxi-distancia entre o ponto P1 com coordenadas (x1, y1) e o ponto P2 em (x2, y2) é |x1 - x2| + |y1 - y2|.
A taxi-distância depende da rotação do sistema de coordenadas, mas não depende de sua reflexão em torno de um eixo ou suas translações. A geometria do taxi satisfaz todos os Axiomas de Hilbert exceto o axioma lado-ângulo-lado, como se pode ver ao gerar dois triângulos, cada um com duas faces e um ângulo sendo o mesmo, e ainda assim sem ser congruêntes.
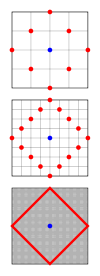
Um circunferência é um conjunto de pontos com uma distância fixa, chamada de raio, até um ponto chamado centro. Na geometria do táxi, a distância é determinada por uma métrica diferente da Euclidiana geometria, e a forma das circunferências também mudam. As táxi-circunferências são quadrados com os lados orientados segundo um ângulo de 45º dos eixos coordenados. A imagem da direita exemplifica porque isso é verdade, mostrando em vermelho o conjunto de todos os pontos com uma distância fixa de um centro, que aparece em azul. Conforme o tamanho das quadras de uma cidade diminuem, os pontos tornam-se mais numerosos e vão formando um quadrado rotacionado em uma geometria do táxi contínua. Enquanto cada face deve ter comprimento √2r usando uma métrica Euclidiana, onde r é o raio da circunferência, seu comprimento na geometria do táxi é 2r. Assim, o comprimento da circunferência é 8r. A equação implícita que representa a taxi-circunferêcia unitária é |x| + |y| = 1 em coordenadas cartesianas e r = 1 / (|sinθ| + |cosθ|) em coordenadas polares.
Uma circunferência de raio r para a distância de Chebyshev (métrica L∞) sobre o plano é também um quadrado com lados medindo 2r, paralelos aos eixos coordenados, então a distância de Chebyshev planar pode ser vista como equivalente por rotação e escalamento à distância do táxi planar. No entanto, esta equivalência entre as métricas L1 e L∞ não se generaliza para dimensões maiores.
Sempre que cada par em uma coleção dessas circunferências tem uma interseção não vazia, existe um ponto de interseção para todos os elementos da coleção; então, a distância de Manhattan forma um espaço métrico injetivo.
Ver também[editar | editar código-fonte]
Referências
- ↑ «Heuristics». theory.stanford.edu. Consultado em 25 de maio de 2023
Bibliografia[editar | editar código-fonte]
- Barroso, M. M. A. A matemática na limpeza urbana: trajetória ótima de um caminhão de lixo. Caxambu, SBMAC, 1998.
- Brandley, M., Square circles, Pentagon, Fall, 1970, p. 8-15.
- Brisbin, Ruth and Paul Artola, Taxicab trigonometry, Pi Mu Epsilon Journal, 8 (1985) 89-95.
- Byrkit, R., Taxicab geometry: A Non-Euclidean geometry of lattice points, Math. Teacher, 64 (1971) 418-422.
- Gardner, M., The Last Recreations, Springer-Verlag, 1997. ISBN 9780387258270
- Golland, L. Karl Menger and taxicab geometry, Mathematics Magazine, vol. 63, 1990. No. 5 (Dec., 1990), pp. 326-327 (o artigo consiste de 2 páginas). Mathematical Association of America.
- Iny, David, Taxicab geometry: another look at conic sections, Pi Mu Epsilon Journal, 7 (1984) 645-647.
- Krause, Eugene F. Taxicab Geometry: An Adventure in Non-Euclidean Geometry. Dover. New York, 1986. ISBN 0-486-25202-7.
- Laatsch, R., Pyramidal sections in taxicab geometry, Math. Magazine, 55 (1982) 205-212.
- Lima, E. L. Espaços métricos. Rio de Janeiro, IMPA, 2003. ISBN 8524401583
- Martin, George Edward. The Foundations of Geometry and the Non-Euclidean Plane, Intext, Educational Publishers, NY. Springer: 1982. ISBN 0387906940
- Mertens, L., A fourth dimensional look into taxicab geometry, J. of Undergraduate Mathematics, 19 (1987) 29-33.
- Miranda, D. F. Geometria Táxi, uma métrica para os espaços geográficos e urbanos uma análise exploratória. Dissertação de Mestrado em Tratamento da Informação Espacial, Belo Horizonte, PUC-MG, 1999.
- Miranda, Dimas Felipe de. Barroso, Leônidas Conceição. Abreu, João Francisco de. Geometria Taxi: Uma Geometria Não Euclidiana Descomplicada. 2005. III - EEMOP.
- Moser, Joseph M. Kramer, Fred. Lines and parabolas in taxicab geometry, Pi Mu Epsilon Journal, 7 (1982) 441-448.
- Reynolds, Barbara E. Taxicab geometry, Pi Mu Epsilon Journal, 7 (1980) 77-88.
- Schattschneider, D., The taxicab group, Amer. Math. Monthly, 91 (1984 423-428.
- Sheid, F., Square circles, Math. Teacher 54 (1961) 307-312.
- Sowell, Katye O. Taxicab geometry: A new slant. Mathematics Magazine, 62 (1989) 238-248.
- Wallen, L. J. Kepler, the taxicab metric and beyond; as isoperimetric primer. The College Mathematics Journal, vol. 26, no 3, 1995.
- Wanderley, Augusto J. M. Carneiro, José Paulo Q. Wagner, Eduardo. Como Melhorar a Vida de um Casal Usando Geometria Não-Euclidiana. Revista do Professor de Matemática [1], número 50.
Ligações externas[editar | editar código-fonte]
- «Distância de Manhattan» - por Paul E. Black (em inglês).
- «City Block Distance», por Kardi Teknomo
- «city-block metric» no PlanetMath
- Eric W. Weisstein, Taxicab Metric at MathWorld.
- «Dicionário de Algoritmos e estruturas de dados» NIST.
- «Taxicab Geometry Bibliography» - Algumas referências de possível interesse.
