Conjetura de Goldbach
A conjetura de Goldbach, proposta pelo matemático prussiano Christian Goldbach, é um dos problemas mais antigos não resolvidos da matemática, mais precisamente da teoria dos números.
Ela diz que todo número par maior que 2 pode ser representado pela soma de dois números primos.
Por exemplo: 4 = 2 + 2; 6 = 3 + 3; 8 = 5 + 3; 10 = 3 + 7 = 5 + 5; 12 = 5 + 7; etc.
Verificações por computador já confirmaram a conjetura de Goldbach para muitos números. No entanto, a efetiva demonstração matemática ainda não ocorreu.
O melhor resultado até agora foi dado por Olivier Ramaré em 1995: todo número par é a soma de no máximo 6 números primos.
Origem[editar | editar código-fonte]
Em 7 de junho de 1742, o matemático prussiano Christian Goldbach escreveu uma carta a Leonhard Euler (carta XLIII) [2], onde ele propôs a seguinte conjetura:

Todo inteiro par maior que 2 pode ser escrito como a soma de 3 números primos.
Ele considerava o número 1 como sendo primo, que uma convenção posterior (e presente até hoje) abandonou. Uma visão moderna da conjetura é:
- Todo inteiro par maior que 5 pode ser escrito como a soma de 3 números primos.
Euler respondeu em uma carta de 30 de junho de 1742 e lembrou Goldbach de uma conversa anterior que eles tiveram ("…so Ew vormals mit mir communicirt haben…"), na qual Goldbach observou que sua conjectura seguia da seguinte declaração
Todo inteiro par maior que 2 pode ser escrito como a soma de 2 números primos.
sendo esta, então, também uma conjectura de Goldbach. Euler adicionou, ainda, que estava absolutamente certo sobre essa última conjectura, mas que não era capaz de prová-la.
A última versão aqui descrita é a mais conhecida e divulgada atualmente, também a mais aceita, por ser mais simples e abrangente.
Também é conhecida como a conjetura "forte" de Goldbach, distinta de seu corolário mais fraco. A conjectura forte de Goldbach implica a conjetura que todos os números ímpares maiores que 7 são a soma de três primos, que é conhecida atualmente como a conjetura "fraca" de Goldbach. Enquanto a conjetura fraca de Goldbach parece ter sido provada em 2013,[1][2] a conjetura mais forte permanece sem solução.
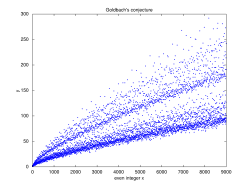
Resultados numéricos[editar | editar código-fonte]
Para valores pequenos de n, a conjetura de Goldbach pode ser testada diretamente (método conhecido jocosamente pelos matemáticos como força bruta e ignorância[3]).
Em 1938, N. Pipping testou todos os números até 105.
Tomás Oliveira e Silva já testou todos os números até 4*1017 [4]

































