Mecanismo de reação
O mecanismo de reação é a descrição da sequência de reações elementares (aquelas que ocorrem em uma única etapa) que ocorrem em uma reação química.[1] Essencialmente, o mecanismo de uma reação fornece a correlação entre os movimentos e colisões moleculares necessários para que uma reação química ocorra, isto é, fornece uma relação entre as posições dos núcleos e dos elétrons nos reagentes, intermediários, complexos ativados e produtos, levando em conta ainda o solvente utilizado em uma determinada etapa. De forma prática, desenhamos as estruturas dos reagentes e indicamos com setas curvas o caminho que os elétrons aparentam tomar durante a reação. Nas grande maioria das reações orgânicas os elétrons partem de uma molécula e se deslocam para outra. As moléculas que tendem a aceitar os elétrons em uma reação são chamadas de eletrófilas (i.e., gostam de elétrons, ou seja carga negativa), enquanto que as moléculas cuja tendência é a doação de elétrons em uma reação é chamada de nucleófilas (i.e. gostam de núcleos, ou carga positiva).[2]
Na teoria cinética é postulado que a lei de velocidades, um resultado macroscópico e determinado sempre empiricamente, é compostos das reações elementares que compõem o mecanismo da reação.[3] Dessa forma, uma mecanismo será tanto mais adequado para descrever uma reação química quanto mais estiver em acordo com a lei de velocidades e outros parâmetros experimentais que podem ser utilizados na inferência do mecanismo, com a formação de intermediários, os efeitos de solvente e catalisadores.
Introdução[editar | editar código-fonte]

Uma transformação química envolve a reorganização de átomos e elétrons entre os reagentes até a formação dos produtos.
A reação passa por um estado de maior energia, denominado estado de transição ou complexo ativado. A diferença de energia entre os reagentes e o estado de transição é chamada de energia de ativação, em uma reação simples. A velocidade de uma reação química depende da energia de ativação, conforme a equação de Arrhenius, obtida experimentalmente. Os parâmetros termodinâmicos podem ser obtidos através da equação de Eyring.
Um catalisador é um agente químico que aumenta a taxa (velocidade) da reação, diminuindo a energia de ativação. O catalisador opera sobre o mecanismo da reação e estabiliza o complexo ativado ou introduz um caminho de menor energia. O catalisador não altera a constante de equilíbrio da reação porque não ocorre variação sobre a diferença de energia entre reagentes e produtos.
Setas curvas[editar | editar código-fonte]
Setas curvas são símbolos utilizados para mostrar, de maneira simplificada, o movimento dos elétrons em uma reação química, o sentido das setas vão dos elétrons de um nucléofilo (espécime doadora), ou de uma ligação pi(π), para o eletrofilo (espécie aceptora). Outra maneira que as setas curvas podem aparecer são como setas incompletas, chamadas de meia setas curvas representam o deslocamento parcial dos elétrons, diferente das completas que é o movimento do par eletrônico inteiro.[2][4]
Tipos de Reações[editar | editar código-fonte]
Há dois tipos de mecanismo, dependendo do número de etapas que contém:
Reações elementares[editar | editar código-fonte]
Transcorre em somente uma etapa. Esta reação se produz com a formação de um só complexo ativado e só tem que superar uma barreira energética. Se representa em uma só equação química.
Reações complexas[editar | editar código-fonte]
Transcorre em duas ou mais etapas, com formação de intermediários. Também podemos dizer que é um conjunto de reações elementares, onde há mais de uma formação de complexos ativados diferentes e supera diferentes barreiras energéticas. Se expressa em várias equações químicas ou uma global. Na equação química global, representa-se o estado inicial e o estado final do global das reações, mas não se apresenta como transcorreu a reação.
Os intermediários são moléculas que aparecem no mecanismo da reação, mas não na equação inicial.
Molecularidade[editar | editar código-fonte]
A molecularidade é o número de moléculas que tomam parte como reativos em uma reação elementar. Dependendo do número de moléculas que participam, se classificam:
- Unimoleculares: participa uma molécula.
- Bimoleculares: participam 2 moléculas.
- Trimoleculares: participam 3 moléculas, improvável do ponto de vista probabilístico.
Estratégia para Dedução de um Mecanismo[editar | editar código-fonte]
A físico-química orgânica fornece uma sequência de etapas lógicas que ajudam na caracterização do mecanismo de uma determinada reação química. O conhecimento do mecanismo de uma reação química é fundamental para pesquisa e o ensino da reatividade química. Uma boa compreensão dos mecanismos ajuda os químicos na proposta de novas reações.[5]
Etapa 1: Identificar os tipos de produtos da reação e classificá-la[editar | editar código-fonte]
O primeiro passo para a determinação de um possível mecanismo para uma determinada reação química é a identificação dos produtos e tentativa de classificação da reação em uma das seis grandes classes.[6][7]
Substituição[editar | editar código-fonte]
Essas reações geralmente possuem estrutura do tipo , com dois reagentes se recombinando para a formação de dois produtos. As reações de substituição acontecem através de mecanismos heterolíticos ou homolíticos.
- Substituição Nucleofílica

Na substituição nucleofílica, um nucleófilo utiliza um par de elétrons não ligantes para estabelecer uma ligação com o substrato; e o nucleófugo (grupo abandonador) quebra sua ligação com o substrato, levando consigo um par de elétrons. Há possibilidade de formação de intermediário carbocátion.
- Substituição Eletrofílica
Na substituição eletrofílica, um eletrófilo atacante remove um grupo funcional do substrato, se adicionando em seu lugar. Nesse tipo de reação, pode haver formação de intermediário carbânion.
- Substituição Radicalar
Nesse tipo de reação, em uma primeira etapa, um radical Y é formado com a quebra homolítica de algum composto contendo o radical Y ligado. Em seguida, o ciclo de propagação se dá com o ataque do radical Y a um composto AX, formando o composto AY e o radical X, que dá prosseguimento ao ciclo.
Adição[editar | editar código-fonte]
Essas reações possuem, normalmente, estrutura do tipo , com dois ou mais reagentes se combinando para a formação de um produto. Essas reações acontecem basicamente através de três mecanismos possíveis: heterolítico, homolítico e pericíclico.[8]
- Adição Eletrofílica (Heterolítico)

No mecanismo de adição eletrofílica, com a aproximação de uma espécie ou um sítio deficiente em elétrons ao sítio da dupla ou tripla ligação, rico em elétrons, um ataque eletrofílico é realizado, com a doação dos elétrons π para a formação de uma ligação com a espécie eletronicamente deficiente. Com a quebra da ligação π, há a formação de um carbocátion, uma espécie bastante reativa, que reage prontamente com uma espécie doadora de elétrons.
- Adição Nucleofílica (Heterolítico)
No mecanismo de adição nucleofílica, um nucleófilo doa um par de elétrons para um dos carbonos participantes da dupla ou tripla ligação, levando a formação de um carbânion. O carbânion, espécie altamente reativa, reage com uma espécie deficiente em elétrons, formando o produto final da adição.
- Adição de Radical Livre (Homolítico)

No mecanismo de adição de radical livre, em uma primeira etapa, há a formação de radicais livres no composto XY a ser adicionado à dupla/tripla ligação através da quebra homolítica da ligação X-Y, dissociada espontaneamente ou por vias fotocatalíticas. O cliclo de propagação se dá pela adição de um dos radicais formados à dupla/tripla ligação, gerando novamente um radical, que induz a clivagem homolítica da ligação X-Y com a abstração de um dos radicais.
- Adição Simultânea (Pericíclico)
No mecanismo de adição simultânea, há uma adição de forma concertada em apenas uma etapa, sem formação de intermediários.
Eliminação[editar | editar código-fonte]

Essas reações geralmente possuem estrutura do tipo , com dois reagentes contribuindo para a formação de três produtos. As reações de eliminação-β acontecem majoritariamente através de mecanismos heterolíticos e pericíciclos; mecanismos homolíticos são raros.
Rearranjo[editar | editar código-fonte]
Os rearranjos, em sua maioria, envolvem a migração de um átomo ou grupo de um átomo a outro. Possuem estrutura do tipo e podem ocorrer principalmente de três formas, envolvendo dois, um ou nenhum elétron.
- Rearranjo Nucleofílico (Par de Elétrons)
Nesse tipo de rearranjo, após a formação de um cátion (comumente um carbocátion), o grupo migratório leva consigo um par de elétrons, deixando o átomo ao qual ele estava originalmente ligado com uma camada de valência incompleta, com um sexteto. A etapa final consiste na restauração do octeto do átomo eletrodeficiente.
- Rearranjo Radicalar (Um Elétron)

No rearranjo radicalar, após a formação de um radical, o grupo migratório leva consigo apenas um elétron, levando o radical a se formar em um átomo diferente do inicial.
- Rearranjo Eletrofílico (Nenhum Elétron)
No rearranjo eletrofílico, após a formação de um ânion (comumente um carbânion), um grupo migra sem seus elétrons, alterando o sítio aniônico da molécula.
Oxidação e Redução[editar | editar código-fonte]

A definição de oxidação e redução para a química inorgânica costuma ser o ganho (redução) ou a perda (oxidação) de elétrons. Para a química orgânica, oxidação é a conversão de um grupo funcional para outro com maior estado de oxidação, sendo redução o contrário. Geralmente, oxidações na química orgânica envolvem aumento do teor de oxigênio e/ou redução do teor de hidrogênio, com o contrário sendo verdadeiro para reduções. Com isso, grande parte das reações de oxidação e redução na química orgânica caem em alguma das classes citadas acima, porém muitos não.
Combinações das Classes Acima[editar | editar código-fonte]

É muito comum encontrar reações que se encaixam em mais de uma classe. Por exemplo, substituições em que ocorre rearranjo no intermediário, adições que levam a redução da molécula, etc. Portanto, deve-se levar as classes acima apenas como uma base para a proposta do mecanismo, sendo necessários outros experimentos e determinações antes de se propor um mecanismo para uma reação.
Etapa 2: Determinar a lei de Velocidades[editar | editar código-fonte]
A velocidade (ou taxa) de uma reação indica o quanto uma reação se processa em certo tempo. Ela pode ser medida com base em quanto de um produto é formado - ou, proporcionalmente, quanto de um reagente é consumido - nesse intervalo.[9] Por exemplo, para uma reação genérica do tipo têm-se que a expressão para a taxa de reação pode ser escrita como
.
Ademais, também espera-se que
,
ou seja, a taxa de consumo do reagente A seja proporcional a concentração do reagente elevada a n, em que n é a ordem da reação no reagente A. A lei de velocidade dessa reação genérica pode, pois, ser definida como:
, em que k é a constante de velocidade da reação.
Dentro do estudo do mecanismo das reações, a determinação da lei de velocidades ocupa um lugar de destaque. Isso se deve ao fato de que o próprio mecanismo de reação pode ser interpretado como uma série de etapas elementares de reação - que, por sua vez, podem ser entendidas como reações envolvendo um pequeno número de moléculas, com leis de velocidade simples - sucessivas.[10] Assim, a lei de velocidade das reações pode dar informações valiosas que contribuem para a eliminação ou que dão base para sustentar de maneira mais própria alguma proposta de mecanismo. Considerando que é impossível provar categoricamente a via em que uma reação se dá, o que se busca é encontrar o maior número de evidências que corroborem a proposta mais adequada.[5]
Deste modo, é possível que se lance mão de uma série de técnicas experimentais para que se obtenha os parâmetros k e n associados à lei de velocidades de cada um dos sistemas em estudo:
Método das Velocidades Iniciais[editar | editar código-fonte]
Nesse método, mede-se a velocidade nos primeiros instantes (possivelmente, os 10% de conversão iniciais da reação) em que a reação ocorre para diferentes concentrações iniciais de reagente.[10] Após isso, relaciona-se o logaritmo das velocidades iniciais (eixo das ordenadas) com o logaritmo das concentrações iniciais (eixo das abscissas). No caso da reação genérica , o ajuste linear desses dados deve retornar uma reta cujos parâmetros são dados por
,
sendo possível obter a constante de velocidade k por meio do coeficiente linear e a ordem de reação n pelo coeficiente angular do ajuste.
No caso de reações mais complexas, com mais de um reagente participando da etapa analisada - por exemplo, - o que se faz é ajustar o sistema estudado para que obtenhamos a lei de velocidade de pseudoprimeira ordem.[10] Nesses ajustes, precisamos fazer com que a concentração de um dos reagentes seja muito maior que a do outro (> 100 vezes) e com esse grande excesso dizemos que a concentração desse reagente não se alterará. Assim:
, que é praticamente constante.
Assim, n, m e k podem ser determinados experimentalmente fazendo correlações simples, como no exemplo anterior.
Leis de velocidade integradas[editar | editar código-fonte]
Se a reação ocorrer tão rapidamente de modo a dificultar a aferição da velocidade inicial ou se houver interesse em expressar a variação da concentração das substâncias envolvidas na reação ao longo do tempo, uma boa solução pra isso é integrar as equações diferenciais que as leis de velocidade representam.[10] No caso, também se compara os dados experimentais aos modelos, analisando para ver se eles se ajustam a eles ou não. A fim de facilitar a análise, as equações de leis de velocidade são dadas em forma de reta. Algumas delas estão colocadas abaixo.
, para reações de primeira ordem (n = 1).
, para reações de segunda ordem (n = 2).
, para reações de n-ésima ordem.
, para reações de primeira ordem em um reagente A e também de primeira ordem em um reagente B.
A dedução dessas equações já é bem conhecida na literatura.[1][10]
Assim, a ordem da reação é dada pelo ajuste dos dados experimentais aos modelos estabelecidos e a constante de velocidade se dá normalmente pelo coeficiente angular retornado pelo ajuste linear dos dados.
Modelos cinéticos mais complexos[editar | editar código-fonte]
É ainda possível que se lide com sistemas mais complexos do que os exemplos citados até agora, como, por exemplo, mecanismos que passem por intermediários ou reações reversíveis que preconizam a existência de um equilíbrio químico. Seja observado o exemplo equacionado abaixo.
No exemplo em questão, pode-se ver dois reagentes A e B reagindo para formar um intermediário I em uma reação reversível. A reação direta é governada pela constante , enquanto a inversa é governada por . Por sua vez, o intermediário I gera o produto P em uma reação governada pela constante . Logo, a expressão da taxa de formação de produto é bem simples.
Há, entretanto, um grave problema: muitas das vezes, não se sabe precisar a concentração do intermediário no meio - há vezes em que é difícil até mesmo precisar a existência de um intermediário, especialmente se esse for de alta energia (e, portanto, de baixa concentração).
Com isso, estuda-se a taxa de formação/consumo do intermediário.
Uma aproximação válida para a simplificação desse problema é a aproximação do estado estacionário. Nessa aproximação, considera-se a hipótese da concentração de intermediário praticamente não se alterar no meio, sendo, portanto, a taxa de formação/consumo do intermediário (d[I]/dt) igual a zero.[10] Assim, é possível obter uma expressão para a concentração do intermediário [I].
Assim, substituindo o valor da concentração de intermediário na expressão para a taxa de formação de produto, têm-se:
Se for considerado a etapa de conversão do intermediário em produto como etapa lenta, , Portanto:
Caso :
Por conseguinte, a lei de velocidade desse exemplo de reação pode ser determinado como uma reação de primeira ordem (ou, ao menos, de pseudoprimeira ordem), como já visto anteriormente.
Etapa 3: Determinar os Parâmetros Termodinâmicos de Ativação[editar | editar código-fonte]
A teoria do estado de transição surge primordialmente como uma consequência do estudo da dependência da constante de cinética em função da temperatura feito por Arrhenius de maneira empírica. Arrhenius percebeu que o efeito da temperatura era tamanho sobre uma reação química que não poderia ser explicado somente como uma mudança na energia translacional dos reagentes. Dessa forma, eram necessárias mais do que colisões entre os reagentes para que uma reação ocorresse, era preciso que os reagentes superassem uma barreira de energia que recebe o nome de energia de ativação.[1] Podemos pensar nas moléculas em uma reação como uma superfície (hipersuperfície, em geral) que descreve a energia das moléculas em função da sua estrutura geométrica. Nesse contexto, a ideia de uma barreira energética implica um máximo superfície sobre a qual as moléculas viajam.[11] Além disso, a descrição dos comprimentos de ligação, ângulos de ligação e os diedros associados que se sucedem durante o fornece a coordenada de reação, cujo máximo indica o estado de transição e a estrutura do chamado complexo ativado.
Encontrando a equação de Eyring[editar | editar código-fonte]
A equação de Eyring foi construída quase que simultaneamente por Henry Eyring, Meredith Gwynne Evans e Michael Polanyi em 1935. [12][13]
Os cientistas tentaram estabelecer uma relação entre o equilibro dos reagentes, [12] com o estado de transição (ET). Para isso parte-se de um equilíbrio proposto, até chegar em uma equação que permite determinar parâmetros termodinâmicos de ativação. A equação também descreve a mudança na taxa de reação conforme a temperatura.
Que tem a seguinte constante de equilíbrio associada:
Como , então.
O complexo ativado se decompõe por decaimento nos produto p, com uma constante .
Como:
.
Agora é preciso obter a constante da reação unimolecular .
O movimento vibratório do complexo ativado ao longo da coordenada de reação, tem associada uma frequência , que também pode ser pensada como sendo a frequência com que os átomos no complexo ativado se aproximam do estado de transição. Por isso, é razoável admitir que a constante cinética do estado de transição seja proporcional a essa frequência de vibração, e assim, , onde é conhecido como coeficiente de transmissão e está associado a probabilidade do produto ser formado a partir do complexo ativado.
Para então obter a constante de equilíbrio, podemos expressá-la em termos das funções de partição molar e então:
Onde:
Como a função de partição do complexo ativado é dada em termos da função de partição vibracional dentro da aproximação harmônica:
Como é muito pequeno comparado com as vibrações anteriores, as constantes de força devem ser muito pequenas da forma que:
Então:
Podendo ser escrito como:
Em que representa a função de partição de todos os outros modos de vibração do complexo. A constante de equilíbrio fica então como:
Onde equivale a uma constante de equilíbrio .
Reunindo as expressões:
Onde é um termo das concentrações.
Determinação dos parâmetros termodinâmicos[editar | editar código-fonte]
Chegando à equação de Eyring, onde é possível realização algumas modificações até chegar aos parâmetros de ativação (∆G‡=∆H‡ - T∆S‡).
A partir da equação de Eyring:
Onde κ é constante para uma dada reação, e ela dita o quanto do estado de transição crítico se transforma em um produto, onde 1 ele é totalmente convertido, e 0,5 somente metade se transforma em produto e a outra metade volta a condição original dos reagentes.[10]
Sabendo que:
Onde ao construir um gráfico de eixos e o eixo , é possível obter esse resultado:
e
Ou seja, a partir de um gráfico é possível determinar os parâmetros termodinâmicos relacionados exclusivamente ao estado de transição (ET). Deve-se observar que para usar tal equação a temperatura deve ser dada em Kelvin.
Etapa 4: Estudo do Efeito do Isótopo na Cinética[editar | editar código-fonte]
Efeito isotópico[editar | editar código-fonte]
O avanço do conhecimento científico nos proporcionou hoje ter uma ideia quase que completa do universo a nível atômico. Entendemos a constituição dos átomos (elétron, próton e nêutron) e de vários fenômenos associados a eles. Um caso associado a essa compreensão é que pelo número de prótons do núcleo diferencia-se os diversos elementos conhecidos.
Quando os átomos de número de prótons iguais (ou seja, mesmo elemento) possuem diferentes números de nêutrons, damos um nome especial para ele: isótopo (iso- mesmo, topo lugar). Pela definição da IUPAC, isótopos são nuclídeos tendo o mesmo número atômico mas diferente número de massa.[14] Em outras palavras, eles são uma variante de um elemento químico diferenciando-se pelo número de nêutrons. Um caso a ser tratado aqui são os de isótopos de hidrogênio no qual se tornam tão especiais que outorgaram nomes diferentes para cada um dos seus isótopos encontrados na natureza.
Apesar de sutil, essa diferença no número de nêutrons contribui para uma discrepância na reatividade das ligações com o deutério comparando com as correspondentes ao hidrogênio. Essas diferenças encontram-se na energia livre e no efeito da diferença de massa na velocidade de passagem sobre a barreira de energia potencial. Além de existir a possibilidade de penetração não clássica sobre a barreira energética[15]
As curvas da energia potencial (potencial de Morse) de uma ligação de hidrogênio e o correspondente de deutério são essencialmente idênticas. A forma do fundo do poço da energia potencial rege a constante de força para a vibração de estiramento, o que pode ser relacionado com a frequência() expressa pela lei de Hooke onde K é uma constante de força e µ é a massa reduzida.
Na mecânica quântica, a energia mais baixa possível para um sistema físico no seu estado fundamental é chamada de energia do do ponto zero (EPZ, sigla em Português para Zero-point energy ). Ela é dada pela expressão:
onde h é a constante de Planck e a frequência .
Como existe uma diferença de massa(µ) nas frequências de estiramento do hidrogênio e deutério e como essas frequências estão relacionadas com a energia do ponto zero, então haverá diferença de energia de ponto zero para uma ligação com o hidrogênio e a ligação correspondente ao deutério. Essa diferença em energia de ponto zero tem duas consequências. Uma vez que o composto de deutério terá a energia de ponto zero mais baixa, será mais estável do que o análogo de hidrogênio. Do mesmo modo, num processo de reação, se considerar a curva relativa à energia potencial do sistema com a distância ao longo da coordenada de reação (figura abaixo), e se se assumir que a ligação em reação é relativamente fraca no complexo ativado em comparação com o fatores, o efeito da energia de ponto zero sobre a reação torna-se aparente. A ligação fraca no complexo ativado reflete em uma baixa constante de força, e uma vez que a diferença de energia de ponto zero diminui com a constante de força decrescente, a diferença de energia de ponto zero para esta ligação no complexo ativado será normalmente pequena. Assim, a diferença de energia de ponto zero nos reagentes resultará numa diferença na altura da barreira (energia potencial) para a reação, e resultará numa maior energia livre de ativação () para o composto contendo deutério. É claro que se assume que as ligações na molécula que não participam na reação não são afetadas durante o processo, e isto parece ser uma boa aproximação na maioria dos casos

Na teoria da taxa absoluta, a taxa de reação é uma função da concentração do complexo ativado e da sua taxa de passagem barreira, conduzindo à equação:
onde é a constante de taxa, é o coeficiente de transmissão, é a massa de o complexo ativado na direção da reação, é o comprimento da região caracterizando o complexo ativado, é a concentração do complexo ativado e e são as concentrações dos reagentes.
Uma vez que a superfície de energia potencial será essencialmente a mesma para um composto de hidrogênio e o seu deutério análogo, é aproximadamente o mesmo para ambos os compostos.[16] Assim, a razão das constantes de taxa será dada pela equação abaixo, assumindo B como sendo o reagente comum:
Os termos de concentração podem ser substituídos por termos de energia livre e os coeficientes de transmissão podem ser assumidos como sendo os mesmos, dando a equação:
A função f é dada por:
Onde os são os números de simetria, , e . Uma expressão semelhante pode ser escrita para . A alta temperatura o primeiro e terceiro termos no produto cancelam, levando a , em que é a diferença em energias de ponto zero dividida por . Uma vez que este termo se aproxima da unidade à medida que a temperatura aumenta, também se torna igual a 1 sob estas condições. A baixa temperatura, o terceiro termo torna-se negligenciável.
A fim de simplificar o cálculo, assume-se geralmente que as ligações não reagentes na molécula não são afetadas durante a reação, só considerando a frequência de estiramento da ligação sujeita a reações. Uma vez que não existe normalmente um conhecimento detalhado da superfície potencial na barreira energética, é geralmente possível determinar apenas o efeito isotópico máximo que corresponde à ausência de ligação ao hidrogênio ou deutério no complexo ativado. Neste caso, torna-se igual a 1 e a equação da razão das constantes de taxa pode ser reescrita como:
onde é expresso em calorias por mol. A razão das frequências vibracionais da ligação ao deutério e da ligação ao hidrogênio é aproximadamente igual a na maioria dos casos e, portanto, cancela o fator de massa, que é aproximadamente igual a . A equação acima é então simplificada, dando a equação abaixo. Em temperaturas mais altas, todos os termos da equação, exceto a massa
O fator cancelará, e o efeito isotópico se aproximará de .
Enquanto a mecânica estatística clássica pode ser utilizada neste tratamento para a maioria dos elementos à temperatura ambiente ou acima, o hidrogênio deve ser devidamente tratado por estatísticas quânticas para permitir a sua natureza ondulatória. Como uma das consequências, o hidrogênio tem a possibilidade de penetração da barreira de energia potencial, também chamado de efeito de tunelamento. Este efeito é previsto como menos provável para o deutério do que para o hidrogênio, e levaria a uma maior diferença na razão de taxas.
Aplicação no estudo dos mecanismos de reação[editar | editar código-fonte]
Dessa diferença vista acima causada pelos isótopos, pode-se tirar algumas informações importantes. A primeira proposta de uso do isótopo é conseguir diferenciar um elemento dos demais em uma certa estrutura química, uma marcação, analisando o que acontece com ele durante a reação química, tanto de forma qualitativa, observando onde o átomo para durante a transformação química ou de forma quantitativa, observando como ele altera as constantes de reação. Nesse contexto temos os efeitos dos isótopos na cinética de reação (KIEs, sigla em inglês para Kinetic isotope effects) que descrevem a diferença na taxa entre dois reagentes marcados isotopicamente[17]
Um KIE é classificado como normal ou inverso com base na magnitude da razão . Para o KIE é considerado normal (o substrato deuterado reage mais lentamente), e para , o KIE é considerado inverso (o substrato deuterado reage mais rapidamente). Os efeitos do isótopo normal são mais comumente atribuídos ao isótopo mais pesado tendo uma barreira de reação mais alta (com o isótopo pesado sendo estabilizado no estado fundamental em relação ao isótopo leve). O caso oposto é encontrado para efeitos de isótopos inversos: o isótopo mais pesado tem uma barreira de reação mais baixa (com o isótopo pesado estabilizado no estado de transição em relação ao isótopo leve). Por exemplo, as reações de eliminação redutiva formadoras de ligações C – H frequentemente exibem um KIE inverso devido a um complexo C – H sigma que é mais estável para as espécies contendo deutério.[18] Mudanças na hibridização de para também comumente dão origem a um KIE inverso.
Um KIE normal ou inverso pode ainda ser identificado como primário ou secundário . Um KIE primário envolve a clivagem e/ou formação da ligação contendo o elemento marcado isotopicamente. Se nenhuma ligação com o elemento marcado isotopicamente for quebrada ou formada, um KIE secundário é observado, com base em influências indiretas. Um KIE primário normal fica entre 2 e 7, enquanto um KIE secundário normal fica entre 0,7, passando por 1 (ou seja, sem efeito), e 1,5. Os valores KIE inversos seguem a mesma tendência, apenas invertidos numericamente. Valores KIE maiores (maiores que 100 em alguns casos) podem indicar tunelamento mecânico quântico; as técnicas de temperatura variável podem distinguir o tunelamento de outras possibilidades (como os efeitos de isótopos de equilíbrio precedentes ou a necessidade de incorporar modelos de mecânica estatística mais complexos)[19][20]
Três tipos de experimentos KIE podem ser realizados: (A) dois experimentos independentes para obter a constante de taxa de reação para reagentes marcados e não marcados. (B) Um experimento de competição envolvendo uma mistura 1: 1 de reagentes marcados e não marcados em um único experimento, com o KIE obtido a partir da proporção de produtos. (C) Um experimento de competição interna envolvendo um reagente parcialmente deuterado com vários locais de reação equivalentes, onde o KIE também é baseado na proporção de produtos. Abaixo temos a ilustração dos três experimentos KIE que podem ser realizados[21]

Cada método fornece informações diferentes.[22] O Método A fornece informações sobre a etapa de determinação da taxa: se um KIE for observado, a posição deuterada está envolvida na etapa de determinação da taxa. Os outros dois métodos não fornecem necessariamente informações sobre a etapa de determinação da taxa porque a substituição isotópica pode afetar a proporção de produtos em etapas posteriores em alguns mecanismos.[23] Os Métodos B e C são particularmente úteis na sondagem da natureza dos eventos de formação ou quebra de ligação que não são limitantes da taxa (e, portanto, não podem ser observados pelo Método A).
Um efeito de isótopo no equilíbrio químico (EIE, sigla em inglês para equilibrium isotope effect ) pode surgir de diferenças na estabilidade relativa de reagentes e produtos marcados e não marcados. Os valores KIE e EIE são categorizados de forma semelhante. Um EIE é obtido através da medição da constante de equilíbrio de uma mistura não marcado (), e comparando ao do sistema marcado, . Em reações de várias etapas, como um caso de pré-equilíbrio, o efeito do isótopo observado será uma composição dos valores KIE e EIE[24]
Cinética por RMN em abundância natural[editar | editar código-fonte]
Ao utilizar a técnica de RMN-H para analisar uma molécula, é possível notar, ao redor dos picos, pequenos picos satélites, oriundos do acoplamento entre H1 e C13 e ao tomar a área total como a área do pico principal somada à área dos dois picos satélite, é possível dividir a área dos picos satélites e se obter a abundância natural dos elementos, como 1,1%, que é a abundância natural do C13.

Foi com essa informação que Daniel A. Singleton descobriu que é possível analisar KIEs se utilizando das razões de abundância de isótopos de moléculas que foram postas a reagir. O experimento de Singleton usou a reação Diels Alder entre isopreno com anidrido maleico, com 98,9% de conversão. Ao fazer alguns estudos com as equações de cinética, ele conseguiu chegar a duas equações a seguir[25]:
-
-
Sendo: R/R0 = Proporção do componente isotópico minoritário no material recuperado comparado ao material de partida; F = Conversão fracional; KIE = 1.05 corresponde a um enriquecimento de 25% do componente que reage mais lentamente a 99% de conversão.
Singleton aplicou este conhecimento em variadas classes de reação para a determinação de KIE de átomos pesados (Lê-se átomo pesado, no contexto do efeito isotópico, qualquer átomo mais pesado que o hidrogênio e seus isótopos) e obteve dados experimentais próximos aos números calculados[26].
Estudo não cinético do efeito isótopo[editar | editar código-fonte]
Era comum o uso de C14, que é um átomo emissor β (elétron) com meia vida de 5730 ± 40 anos, para mapeamento de moléculas, que por ser radioativo, pode marcar chapas de revelação, mostrando quais moléculas possuíam o C14.
Atualmente, não é necessário somente o uso de C14, mas Deutério e C13, podendo descobrir qual foi o mecanismo de reação utilizado.

Foi com essa ideia que o íon fenônio foi descoberto, tentando entender o porquê de haver racemização dos produtos marcados com isótopos na seguinte reação[27]:

Etapa 5: Determinar as Correlações Lineares de Energia Livre para Reação[editar | editar código-fonte]
Os mecanismos de reação estudados na química orgânica são um conjunto de ideias que seguem a criação de um modelo para explicar como a reação deve ocorrer baseando-se em dados experimentais.[5] Em geral, os dados experimentais mostram de maneira clara como são os reagentes e os produtos, mas não como ocorre a conversão. A teoria proposta, em 1889, por Svante Arrhenius, cuja equação proposta foi desenvolvida a partir dos estudos de Jacobus van’t Hoff, mostrava que em dado momento da reação um tautômero “ativado” era formado a partir de um “inativado”, sendo esse formado de maneira endotérmica.[28] Esse tautômero mais a frente seria chamado de complexo ativado por Henry Eyring.[29]
Em suma, o complexo ativado não seria capaz de ser detectado e apenas em técnicas mais avançadas, como é o caso da espectroscopia em femtosegundo, que trouxeram inovações apenas em 1990.[30] Dessa forma, o estado de transição era visto como uma pista para prever a formação dos produtos. Dessa forma, em 1935, o trabalho de Henry Eyring deu pistas sobre o comportamento energético para se atingir o estado de transição.[29] Um responsável por encontrar um modelo para o estado de transição foi Louis Plack Hammett.
A Equação de Hammett[editar | editar código-fonte]
Hammett estudou os efeitos de substituintes em derivados de ácidos benzóicos, atribuindo substituintes (X) em posições meta e para, conforme a figura abaixo.

Assim, o trabalho apresentado por Hammett, em 1937, mostrou como os efeitos eletrônicos dos substituintes afetavam a estabilização da carga negativa oriunda da desprotonação dos derivados do ácido benzoico. Dessa maneira, o ácido benzoico foi tomado como referência, onde sua constante de equilíbrio foi dada por K0, enquanto que os seus derivados tiveram suas constantes de equilíbrio determinadas por K.[31] Dessa maneira, Hammett enunciou que:
Manipulando a equação é possível obter:
Reorganizando foi observado que:
Dessa forma, Hammett chamou e . Sendo assim, a equação fica:
Cada grupo X possui a capacidade de doar elétrons para o anel, chamados de grupos doadores de elétrons, ou retirar elétrons do anel, chamados de grupos retiradores de elétrons. Para cada grupo foi possível calcular o valor de σ, uma vez que seu valor é apenas inversamente proporcional a constante dos gases. Os grupos doadores tiveram o valor da constante como negativa, enquanto os valores para os grupos retiradores foram negativos. Dessa maneira, Hammett construiu um gráfico que levasse em consideração os valores de σ e de log(K/K0), conforme visto abaixo:

Analisando o gráfico que pôde ser construído com os valores encontrados mostrou que o melhor ajuste foi uma reta o que proporcionou a interpretação de que o ρ como o coeficiente angular da reta.[32] Dessa forma a equação apresentada ficou conhecida como equação de Hammett.
Além da análise do equilíbrio químico, a constante de velocidade k pode ser expressa em função da constante de equilíbrio K conforme a equação abaixo[33]:
onde G e x são constantes. Isso mostra a relação de Brønsted para a catálise ácida:
Isso viabilizou expressar a equação de Hammett através das constantes de velocidade, conforme a equação abaixo.[8]
Manipulando a equação de catálise proposta por Brønsted, teremos, para:
Sabendo que e , então, multiplicando a equação acima será visto que:
Sendo assim, a relação entre as energias livres é linear, por conta disso há uma correlação linear de energia livre.[6] Essa correlação permitiu que os efeitos dos substituintes fossem de um patamar qualitativo para um patamar quantitativo.
A constante de reação ρ (rho)[editar | editar código-fonte]
A equação de Hammett viabilizou uma relação quantitativa entre a velocidade de uma reação de um composto substituído em meta ou para, com o efeito que esse substituinte possui na perda do hidrogênio ácido presente nos derivados de ácidos benzoicos. Além disso, há uma relação das constantes de velocidade e equilíbrio de grupos de reações similares, como uma relação entre séries de reações de substituição.[34]
Essa similaridade das reações viabilizou a análise entre a hidrólise dos derivados de benzoatos de etila e a ionização do ácido benzoico, possibilitando a comparação entre a constante de velocidade de hidrólise em relação a equação de Hammett, o que mostrou uma correlação linear.[35]

Essa comparação mostrou que a equação de Hammett também é aplicável a outros compostos. Além disso, a diferença entre cada equação será o valor da constante de reação que pode ter um valor maior ou menor. Sendo assim, a inclinação da reta, oriunda do gráfico que relaciona a constante do substituinte com o logaritmo da razão das constantes de velocidade, terá sua inclinação maior ou menor. Por conta da mudança em seu valor, a constante de reação pode ser interpretada como a suscetibilidade da reação ou equilíbrio em relação aos efeitos do substituinte, ou seja, o quanto a reação ou equilíbrio são sensíveis à doação ou recepção de elétrons imposta pelo substituinte.[36]
Com a possibilidade de estudo de compostos similares ao ácido benzoico, outros foram comparados para que os valores de ρ fossem avaliados e comparados. Os valores apresentados por Hammett foram todos positivos, entretanto algumas reações apresentaram valores negativos para ρ.[37]
A diferença observada no sinal de ρ possibilitou a avaliação do mecanismo da reação, uma vez que as cargas são diferentes.[6] Dessa forma, a diferença de carga entre o estado de transição e o reagente é estabilizada ou não pelo tipo de substituinte ligado ao anel aromático. Assim, substituintes doadores de elétrons estabilizam um estado de transição que apresenta carga mais positiva em relação ao reagente. Por outro lado, substituintes retiradores de elétrons estabilizam um estado de transição que apresenta maior densidade de carga no átomo ligado ao anel aromático sendo monitorado em relação ao reagente.[36]
De modo resumido tem-se que[11]:
- ρ > 0: A reação em análise mostra um estado de transição com maior densidade do que esse mesmo átomo nos reagente ), sendo que grupos substituintes retiradores de elétrons "drenam" esse excesso de densidade eletrônica, estabilizando o estado de transição, portanto aumentando a constante de velocidade;
- ρ = 0: A reação em análise mostra um estado de transição com densidade eletrônica igual a reagente no átomo "marcado", portanto as constantes de velocidades (e barreiras reacionais) sendo insensíveis ao substituinte;
- ρ < 0: A reação em análise mostra um estado de transição com deficitário em termos de densidade eletrônica no átomo sendo monitorado em relaque esse mesmo átomo no reagente (), de modo que substituintes doadores de elétrons ajudam a suprir densidade eletrônica a esse centro reacional, estabilizando o estado de transição.
É importante ressaltar que o valor da constante de reação é medida quantitativamente a partir da equação de Hammett e que como o cálculo de seu valor indica, ela é dependente do solvente e da temperatura, conforme mostra a tabela a seguir para algumas reações e equilíbrios[38]:

Dessa forma, o grupo aromático substituído se torna um marcador para avaliar a carga apresentada pelos estados de transição, ou seja, a carga desenvolvida pelo ponto da molécula que participa diretamente da reação química.
A constante do substituinte σ (sigma) para posições meta e para.[editar | editar código-fonte]

A utilização de diferentes substituintes em posições meta e para foram verificadas por Hammett e utilizadas para aferição quantitativa de seus efeitos frente a ionização do ácido benzoico, o que viabilizou a construção da equação de Hammett, como já apresentado.
Essa avaliação foi inicialmente verificada pela mudança no pKa das substâncias o que torna, para o experimento envolvendo o ácido benzoico, o valor para ρ = 1.[31] Dessa maneira, os valores de σ foram calculados conforme a equação abaixo:
Assim, alguns valores de sigma, em relação ao pKa dos substituintes do ácido benzoico são mostrados na tabela 2 [39].
Para facilitar a observação, algumas literaturas tratam os valores para substituintes em meta como σm, enquanto que, em para, σp.
Sendo assim, para cada um dos substituintes foi atribuído um valor de σ relativo ao experimento com os substituintes do ácido benzoico de maneira que o melhor ajuste para a dispersão dos pontos é uma reta de coeficiente angular ρ.
Constante σ (sigma) para ressonância direta com o sítio da reação[editar | editar código-fonte]
Apesar do ajuste referente a σm e σp, alguns experimentos mostraram falta da linearidade proposta por Hammett, principalmente nos experimentos de solvólise do cloreto de terc-cumila (principalmente a solvólise do cloreto de p-metóxi-terc-cumila) e da desprotonação de fenóis (principalmente do p-nitrofenol).[40]

Ambas reações geram uma carga que pode ser estabilizada pelo grupo ligado ao anel aromático. No caso da solvólise do cloreto de terc-cumila, uma carga positiva é formada e estabilizada por substituintes doadores de elétrons, enquanto na reação envolvendo a desprotonação do fenol, a carga negativa é estabilizada por substituintes receptores de elétrons.[40][41] Para levar em consideração a estabilização da carga pela ressonância direta dos substituintes ligados ao anel, foram introduzidas outras constantes de substituintes, uma, denominada σ+, leva em consideração a sensibilidade do centro catiônico do estado de transição em relação à ressonância proporcionada pelos substituintes doadores de elétrons, enquanto a outra, denominada σ- , leva em consideração a sensibilidade do centro aniônico do estado de transição em relação à ressonância proporcionada pelos substituintes retiradores de elétrons.[6]
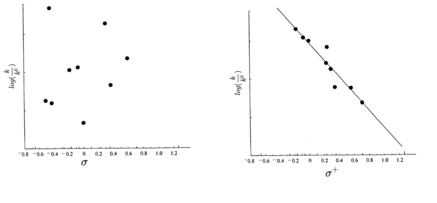
A ressonância direta é mais perceptível em substituintes em posição para e por conta disso, as constantes σp+ e σp- são mais vistas, enquanto os valores de σm+ podem ser observados, mas substituintes fortemente doadores de elétrons não são comumente utilizados na posição meta, mas os valores de σm- são basicamente os mesmos valores de σm, apesar de substituintes retiradores também não serem comumente utilizados em posição meta.[40][41][42]
Dessa maneira, a avaliação da estabilização adicional por meio da ressonância pode ser colocada na equação de Hammett por meio de uma correção desenvolvida por Yukawa e Tsuno, de maneira que a equação ficou conhecida como equação de Yukawa-Tsuno[43]:
Onde . Além disso, r mede a influência da ressonância direta do substituinte com o sítio da reação.
Influencias dos efeitos polares, de ressonância e estéricos na constante σ (sigma)[editar | editar código-fonte]
A ideia de uma constante de substituinte em relação a estabilização da diferença de carga gerada no estado se faz por meio de 2 principais efeitos eletrônicos: efeitos polares, principalmente por efeitos de campo/indutivos e efeitos de ressonância. A primeira ideia sobre o assunto foi idealizada por Swain e Lupton, onde σ sofreria influência de efeitos polares (indutivo/ de campo) por meio da constante representando a colaboração dos efeitos polares do substituinte, bem como por meio da constante que representa a colaboração dos efeitos de ressonância. Além disso, a ideia proposta ainda leva em consideração os valores f e r que são chamados de fatores de ponderação e verificam a sensibilidade do sítio da reação em relação aos substituintes.[32] Sendo assim, a constante sigma fica:
E assim, a de Swain-Lupton tornou-se um acréscimo à equação desenvolvida por Hammett:
Swain e Lupton desenvolveram um trabalho de mapeamento dos valores de e , de maneira que a investigação teve início com a análise dos efeitos puramente polares, ou seja, análises para encontrar valores de . Nesse caso, o estudo foi desenvolvido na dissociação de ácidos biciclo [2.2.2] octano-1-carboxílicos 4-substituídos em solução de etanol e água a 50%. Como a consideração foi de que não houvesse qualquer efeito de ressonância, então o valor de , além de adotar para essa classe de dissociações o valor de , o que resultou em[32]:
Dessa maneira, foi criada uma nova escala de constantes de substituintes, onde a igualdade era observada. Essa escala foi intitulada .
Além disso, quando o substituinte fosse o trimetil-amônio o valor de foi adotado como sendo 0, uma vez que, por não ter elétrons livres, não possui capacidade de proporcionar ressonância e o valor de para a dissociação do ácido benzoico para substituído. Com esse substituinte, o valor de f encontrado foi de 0,56 o que viabilizou o cálculo de , uma vez que também havia a escala .[44]
Em outro artigo, utilizando um ajuste pelo método de mínimos quadrados, Swain redefine a escala utilizada, atribuindo os valores de para o H com substituinte e os valores de para o substituinte NO2. Além disso, foram consideradas as condições de para a dissociação de ácidos ciclohexacarboxílicos substituídos em posição 4 e com isomeria trans, bem como o valor de foi mantido para quando o trimetil-amônio é o substituinte.[45]
Uma outra maneira de observar a influência dos efeitos de ressonância foi desenvolvida por Taft, que levava em consideração os efeitos polares e de ressonância possibilitando a separação entre constantes sigma relativas aos efeitos polares e de ressonância. Os efeitos de ressonância, por ser uma interação que envolve orbitais paralelos, não é tão eficiente e por deslocalizar elétrons acabam sendo altamente polarizadoras. Por outro lado, ainda que o efeito de ressonância possa ser diminuído, o efeito polar não é alterado na posição meta não se altera.[36] Por conta disso é possível afirmar que:
Onde
Ou seja, o substituinte em posição meta proporciona apenas os efeitos polares, enquanto o substituinte em para oferece efeitos tanto polares quanto de ressonância.[36]
A ideia de Taft e Lewis foi conseguir separar a equação de Hammett em relações individuais para cada efeito, tanto o de ressonância quanto os efeitos polares. Dessa maneira foi enunciada a equação de dupla constante de substituinte[46]:
Em dois artigos, Topsom desenvolveu cálculos teóricos em que houve a análise de efeitos polares, de ressonância e eletronegativos dos substituintes. Com isso, foi concluído que em geral os efeitos de ressonância envolvem a interação entre os orbitais π do aromático com os orbitais do mesmo plano que estão nos substituintes e por conta disso se manifestam de maneira alternada, e por tanto nas posições orto e para.[36][47]
Taft também analisou outros possíveis efeitos que não fossem polares ou de ressonância. Esses outros efeitos analisados tinham a geometria do substituinte como foco da análise, ou seja, os efeitos estéricos proporcionados pelo substituinte. Taft, analisando a hidrólise de ésteres, separou os efeitos como eletrônicos e estéricos, como visto abaixo[48][49]:
Onde, são os efeitos eletrônicos e , os efeitos estéricos.
É importante observar que os efeitos indutivos eram gerados pela eletronegatividade, o que permite uma separação entre os efeitos indutivo e de campo. Dessa maneira, pode-se considerar de maneira separada todos os efeitos, como os efeitos de campo (F), de ressonância (R), indutivos (χ) e de polarizabilidade (α)[11]:
Efeitos polares e estéricos em sistemas alifáticos[editar | editar código-fonte]
As análises de Taft referentes ao efeito estérico não se limitou a compostos aromáticos. Taft avaliou a influência dos substituintes na hidrólise de ésteres aromáticos e alifáticos, o que o permitiu avaliar os efeitos causados pelos substituintes em compostos alifáticos. Em geral, a hidrólise se deu a partir da catálise ácida e básica. A ideia observada para anteriormente para os efeitos em um éster aromático, aqui é utilizado apenas para ésteres aromáticos, sendo assim, os efeitos eletrônicos basicamente não são observados e por isso apenas os efeitos estéricos seriam observados, o que tornariam a equação de Hammett como:
Falhou a verificação gramatical (SVG (MathML pode ser ativado através de uma extensão do ''browser''): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "http://localhost:6011/pt.wikipedia.org/v1/":): {\displaystyle log(\frac{k}{k^0})_A = E_s }
Apesar disso, Taft percebeu que tanto na catálise ácida quanto básica, os intermediários das reações seriam diferentes principalmente em 2 pontos: a primeira sendo presença de 2 hidrogênios a mais no intermediário da catálise básica do etanoato de metila (éter etílico metílico) em relação a sua catálise ácida, e a segunda, a presença de cargas negativas na catálise básica, enquanto na catálise ácida as cargas presentes eram positivas.[11]

A presença dos hidrogênios não é extremamente determinante, porém a presença das cargas não pode ser desprezada, o que permitiu Taft propor uma constante de substituinte que mensurasse os efeitos polares em alifáticos, o qual recebeu o símbolo σ*. Além disso, a referência utilizada foi a metila como substituinte, tendo sido escolhido como referência, ou seja, para a metila = = 0.[50]
Sendo assim, Taft propôs uma equação para compostos alifáticos, a qual ficou conhecida como equação de Taft:
Onde ρ* é a sensibilidade em relação ao substituinte e δ, a sensibilidade em relação aos efeitos estéricos.[11]
Vale ressaltar também que, uma vez que pautado na avaliação dos efeitos do substituinte nas catálises ácida e básica, o cálculo da constante de substituinte, devido aos efeitos polares em alifáticos pode ser calculado por[51]:
Dessa maneira, observando todos as constantes observadas até aqui, pode-se construir uma tabela contendo um apanhado de constantes já vistas[6][11][50]:

Desvios da linearidade[editar | editar código-fonte]
Em geral, os gráficos trabalhados nos estudos de mecanismos de reação utilizando o trabalho de Hammett, geram um ajuste linear com as constantes de substituintes. Dessa maneira, os valores associados para ρ são positivos ou negativos. Apesar disso, os valores nem sempre são enquadrados na linearidade independente da constante do substituinte utilizada (seja utilizando σ, σ* ou qualquer outro), ou seja, o gráfico plotado desvia da linearidade esperada[32].
A linearidade mostra a relação em como a carga desenvolvida no estado de transição se comporta com os substituintes adicionados, mas o desvio da linearidade mostra uma mudança na carga desenvolvida no estado de transição conforme os substituintes são trocados. Em geral, a mudança de cargas no estado de transição e consequentemente a não linearidade do gráfico, indicam uma mudança no mecanismo da reação por conta da estabilidade proporcionada para cada substituinte adicionado[11].
Um exemplo para isso é a análise a competição em mecanismos de substituição nucleofílica, conforme descrita abaixo:
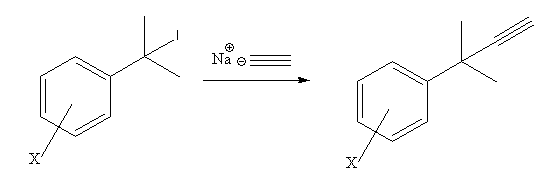
Nessa reação, a presença de grupos retiradores de elétrons atrapalham a saída do Iodo, uma vez que uma carga positiva bem pronunciada seria formada no estado de transição, ou seja, o mecanismo seria favorecida. Por outro lado, quando grupos doadores de elétrons são adicionados ao invés de grupos retiradores, a carga positiva pode ser formada, uma vez que ela seria estabilizada por esses grupos. Sendo assim, o iodo poderia deixar a molécula e um carbocátion seria formado. Nesse caso, o mecanismo pode ser favorecido[11][6]. Dessa forma, o plote do gráfico de por ficaria:

Etapa 6: Investigação dos Possíveis Intermediários Reativos[editar | editar código-fonte]
Intermediários reativos são uma espécie química com certo grau de instabilidade e estão presentes em reações que ocorrem em etapas, as reações multipassos. Os intermediários têm vida curta e são importantes na descrição do mecanismo de reação, aparecendo entre os substratos de partida e o produto estável. Podem ser formados na interação entre reagentes e substratos, por dissociação de compostos orgânicos ou pela promoção de moléculas a estados excitados por absorção de luz e interação com radiação de alta energia. Alguns compostos são estáveis por si próprios e outros são reativos tornando impossível o isolamento. As espécies mais estáveis podem ser detectadas de forma direta com espectroscopia ou aprisionamento químico enquanto as instáveis são detectadas de forma indireta como por interferência de resultados cinéticos.[52]
O estudo de mecanismo de reações é importante para revelar as interações entre essas espécies deficientes e ricas em elétrons com uma descrição detalhada das mudanças na estrutura da ligação durante a reação.
A partir da constante de equilíbrio químico, calculada pela relação entre as concentrações de produtos e reagentes, é possível identificar algumas características da reação. Keq > 1 tem produtos mais estáveis e consequentemente maior concentração, já Keq < 1 tem reagentes mais estáveis. Além disso, de acordo com as constantes K1 como a constante de formação do intermediário a partir do reagente e K2 a formação do produto a partir do intermediário K1 > K2 indica intermediários isoláveis ou uma espécie em rápido equilíbrio com reagentes, agora se K1 < K2, os intermediários não são isoláveis.[52]
Algo a ser levado em consideração é a característica do solvente, que desempenha papel importante na determinação das energias livres relativas do reagente e do estado de transição, consequentemente a taxa de reação. O aumento na constante dielétrica do solvente leva a diminuição da energia necessária para separar as cargas e o seu poder de solvência pode auxiliar na estabilização do estado de transição por solvatação de ambos os íons como solvente prótico.
Neste ponto vale ressaltar a diferença entre estados de transição e os intermediários reativos. O estado de transição não pode ser isolado por não ser uma molécula real. Apresenta ligações parcialmente formadas/quebradas e com mais átomos no entorno de grupo central além do permitido pela regra de ligação de valência e tem energia mais alta que a dos reagentes e produtos, sendo a energia de ativação a energia necessária para atingir o estado de transição. Já os intermediários reativos são moléculas com mínimo de energia local e ligações totalmente formadas e existindo por algum tempo finito com algum nível de estabilidade.[52]
Tipos de Intermediários[editar | editar código-fonte]
Os intermediários reativos podem ser carregados como carbocátions e carbânions, ou neutros reativos deficientes em elétrons como radicais, carbenos, nitrenos e arinos.
Carbocátions[editar | editar código-fonte]
Carbocátions são os intermediários reativos mais importantes com carga formal positiva no carbono. Ou seja, são cátions de carbono. Eles podem ser formados pela remoção de um substituinte e seu par de elétrons, acarretando uma hipovalência, para formar os íons carbênio, ou se um carbono com hibridização sp3 for atacado por um eletrófilo ele pode formar um carbono hipervalente, chamado de íon carbônio.[11]
Durante a década de 1960 e 1970 o professor George A. Olah criou um método para preparar carbocátions de longa duração em altas concentrações, o que possibilitou os estudos de estrutura, estabilidade e reação. Essa produção inicial foi feita com adição de solventes que não reagiam com os cátions, em baixas temperaturas e com adição de superácidos e assim, foram descobertos dois grupos de carbocátions: os trivalentes ou íons carbênio com o átomo de carbono positivo rodeado por três átomos, e os íons carbônio com átomos de carbono positivo e rodeado por cinco átomos (pentacoordenados). Desde então, tornou-se um grupo bem estabelecido com numerosas transformações sintéticas. O íon carbônio é uma espécie formada pela adição de uma carga positiva em um átomo de carbono neutro tetravalente. O íons carbênio é formado por dissociação heterolítica de uma ligação de carbono. Um modelo de carbocátions mais comum é espécie plana com hibridização sp2.[52]
Os carbocátions estão presentes em reações como: reações de substituição nucleofílica (SN1) e eliminação (E1), adições de eletrófilos a ligações duplas e triplas, substituição eletrofílica aromática, adições a compostos de carbonila e química de enolato.[11]
Carbânion[editar | editar código-fonte]
Carbânion é uma unidade com carga negativa em um átomo de carbono e é uma base/ nucleófilo dependendo da condição da reação. São bases de Brønsted porque seus ácidos conjugados são fracos. São espécies trivalentes com hibridização sp3, com geometria tetraédrica.[52]
Radicais Livres[editar | editar código-fonte]
Radical ou radical livre é um grupo substituinte preservado como uma unidade por meio de uma transformação química. Os radicais centrados em nitrogênio e oxigênio são menos estáveis que os centros em carbonos radicais, sendo mais elevados em energia pela eletronegatividade comparado ao carbono.
Hoje, os radicais são reconhecidos como participantes de reações seletivas e sua química oferece método viável aos métodos iônicos tradicionais. Como vantagens, os radicais são neutros e, por isso, são muito menos solvatados do que carbocátions ou carbânions. Portanto, eles são menores e podem operar em ambientes polares. Ao contrário dos carbocátions, os radicais em geral são menos propensos a rearranjos.[52]
Uma das principais desvantagens da química de radicais livres é que eles reagem prontamente com o oxigênio, o que significa que suas reações devem ser realizadas sob uma atmosfera inerte.
Carbeno[editar | editar código-fonte]
Derivados divalentes de carbono altamente reativos, neutros, tendo apenas 6 elétrons de valência com carga formal igual a zero. Apresentam duas ligações covalentes (envolvendo elétrons) e dois elétrons não ligados localizados no átomo de carbono e um orbital vazio, o que torna o carbeno muito reativo.[52]
Classificados como singletos ou tripletos dependendo da estrutura eletrônica e das energias relativas dos dois orbitais não ligados, sendo o singleto com um par de elétrons no orbital molecular mais ocupado HOMO σ e orbital π vago, com estrutura sp2. Por isso, exibem caráter nucleofílico e eletrofílico. Os tropletos tem 2 elétrons desemparelhados e podem ser híbridos sp2 ou linear sp, sendo a maioria não linear.[52]
A formação do carbeno ocorre de duas formas: decomposição de moléculas reativas ou eliminação de duas ligações de um carbono tetravalente.
Nitreno[editar | editar código-fonte]
Nitrenos são moléculas diatômicas NH e seus derivados N-raros. São intermediários neutros, formado termicamente ou fotoquimicamente de ácido hidrazóico ou azidas orgânicas. São os análogos do nitrogênio dos carbenos e o N tem 6 elétrons em sua camada de valência, sendo um eletrófilo.
Arinos[editar | editar código-fonte]
Arinos e heteroarinos são originadas da remoção de dois substituintes adjacentes de anéis aromáticos ou heteroaromáticos, deixando dois elétrons distribuídos entre dois orbitais, gerando uma ligação tripla forçada. Na maioria dos casos os substituintes são orto entre si, porém meta e para arinos também são intermediários possíveis. O exemplo mais comum é o próprio benzeno.
A principal aplicação de arinos em síntese é na construção de polímeros policíclicos. Além disso, também é utilizado na preparação de isômeros incomuns de compostos aromáticos.
Técnicas de determinação[editar | editar código-fonte]
Para determinação dos intermediários reativos são utilizadas algumas técnicas de espectroscopia, espectrometria e estudos relacionados a mecânica de reação.
Espectrometria de massa pode ser utilizada para determinar a massa de uma molécula e sua composição atômica. Espectrometria de RMN revela o esqueleto de carbono da molécula. Espectroscopia na região do infravermelho (IV) para determinar grupos funcionais da molécula. Espectroscopia na região do ultravioleta-visível (UV-Vis) é usado para detectar cromóforos presentes na molécula ou espécie sendi investigada. O método espectroscópico fornece evidências valiosas para a intermediação de espécies, a sensibilidade inerente a técnica permite que sejam utilizados para detectar concentrações muito baixas, porém não fornece detalher estruturais como IV ou RMN.
Estudos de mecânica usam isótopos estáveis como 2H, 13C, 15N, 17O e 18O e sua posição é determinada por RMN.
Além disso, utiliza-se técnicas mais atuais como Espectroscopia de ressonância de spin de elétrons (ESR) fornece evidências únicas nos casos em que há elétrons desemparelhados como radicais livres e estados triplos de carbenos ou nitrenos. Já a técnica polarização nuclear dinâmica induzida químicamente (CIDNP) envolve acoplamento de pares de radicais.
Etapa 7: Estudo da Estereoquímica da Reação[editar | editar código-fonte]
Quando Louis Pasteur em 1848 na École Normale de Paris realizou um conjunto de observações, que tinham como descrição que a atividade óptica de soluções orgânicas é determinada pela assimetria molecular, que produz estruturas imagem especulares não sobrepostas, é que o mundo foi apresentado a possibilidade das moléculas orgânicas terem estruturas tridimensionais. Estudo esse que carrega a contribuição que Jean-Baptiste Biot deixou, quando, em 1815 descobriu que algumas moléculas são capazes de girar o plano de luz polarizada. Uma extensão lógica desta ideia ocorreu em 1874 quando uma teoria de estrutura orgânica em três dimensões foi avançada independentemente e quase simultaneamente por Jacobus Henricus van't Hoff na Holanda, e Joseph Achille Le Bel na França. Nessa época era sabido pelo trabalho de Kekulé em 1858 que o carbono era tetravalente (ligações com quatro outros grupos ou átomos). van't Hoff e Le Bel propuseram que as quatro valências do átomo de carbono não eram planas, mas direcionadas ao espaço tridimensional. van't Hoff propôs especificamente que a disposição espacial era tetraédrica. Um composto contendo um átomo de carbono substituído por quatro grupos diferentes, que van't Hoff definiu como um carbono assimétrico, seria, portanto, capaz de existir em duas formas distintas, não sobreponíveis. O átomo de carbono assimétrico, eles propuseram, foi a causa da assimetria molecular e, portanto, da atividade óptica.[53] Com isso, a estereoquímica estava inaugurada, expandindo ainda mais a riqueza estrutural que compostos orgânicos apresentam. Com o avanço da síntese orgânica e da importância da mesma na sociedade moderna, aumentou a necessidade de se compreender o enigma da reatividade química, desse modo, tentando elucidar de forma detalhada as sequências elementares que levam uma mistura de reagentes a formar um determinado produto é que estratégias para a investigação de mecanismo foram elaboradas. Como um braço desse processo é que a estereoquímica é estudada como uma etapa importante na dedução do mecanismo de reação.
Como a estereoquímica afeta o resultado de uma reação[editar | editar código-fonte]
Para entender como a estereoquímica interfere no resultado de uma determinada reação, alguns cenários serão examinados.
Reações de moléculas quirais que não ocorrem no centro estereogênico[editar | editar código-fonte]
Se uma reação de um composto quiral não formar ou clivar quaisquer ligações ao centro estereogênico, então a configuração do produto é a mesma do reagente. Portanto, podemos estabelecer a configuração absoluta de moléculas particulares usando moléculas de referência de uma configuração. Por exemplo, 2-metilbutan-1-ol é convertido em 1-bromo-2-metilbutano por HBr. A reação não ocorre no centro estereogênico. Portanto, o (S)-2-metilbutan-1-ol produz (S)-1-bromo-2-metilbutano.[54]

Estereoquímica de uma reação de substituição em um centro estereogênico[editar | editar código-fonte]
Se uma ligação a um carbono com centro estereogênico se romper durante uma reação, existem várias possibilidades:
(a) A ligação é rompida e a nova ligação é feita em uma única etapa ou de forma concertada. Nessa situação, a estereoquímica será invertida.
(b) A ligação é quebrada e uma nova ligação é feita em duas ou mais etapas (ou seja, por meio de intermediários). Nesse caso, a estereoquímica pode se tornar menos distinta e pode levar a uma mistura racêmica (mistura 50:50 de enantiômeros).[55]
a) Reação SN2:

Podemos explicar a inversão de configuração imaginando que o íon hidróxido ataca (R) - 2-bromooctano no átomo de carbono do lado oposto ao eixo da ligação C-Br. Assim, é razoável propor um estado de transição linear no qual o centro estereogênico tem ligações parciais aos íons hidróxido e brometo.[54]

b) Reação SN1:

O íon iodeto está atacando o haleto de alquila, mas, neste caso, a reação ocorre em duas etapas. Após a primeira etapa, um intermediário aquiral é formado (carbocátion), e isso levará a uma mistura racêmica (50:50) de enantiômeros para o produto quiral.[54]
Estereoquímica de uma reação radicalar[editar | editar código-fonte]
Na reação radicalar do bromo com (S)-1-cloro-2-metilbutano, um átomo de bromo substitui um átomo de hidrogênio no centro estereogênico terciário para dar uma mistura racêmica de (R)- e (S)-2-bromo-1-cloro-2-metilbutano.

Este resultado experimental indica que o intermediário radical livre produzido no curso da reação é aquiral. Portanto, a reação do radical com bromo pode ocorrer com probabilidade igual de ataque tanto por baixo quanto por cima, dando uma mistura de 50:50 de enantiômeros.[54]

Reações que produzem centros estereogênicos[editar | editar código-fonte]
Estereoquímica da adição Markovinikov a alcenos[editar | editar código-fonte]

Vamos examinar a estereoquímica da adição do ácido bromídrico ao but-1-eno para dar 2-bromobutano. Sabemos que esta é uma adição Markovnikov. Um próton é adicionado ao but-1-eno em C-1 para dar um carbocátion secundário. É aquiral porque tem um plano de simetria. O carbocátion é atacado pelo íon brometo nucleofílico com igual probabilidade do lado superior ou inferior do intermediário planar. O ataque na parte superior fornece o enantiômero S, enquanto que o ataque na parte inferior fornece o enantiômero R, resultando em uma mistura racêmica.[54]

Estereoquímica da reação de bromação em alcenos[editar | editar código-fonte]
Lembramos que a reação do bromo com um alceno dá um produto com átomos de bromo em átomos de carbono adjacentes. Por exemplo, o but-2-eno reage com o bromo para dar 2,3-dibromobutano. Dois centros estereogênicos equivalentemente substituídos se formam nesta reação. Existem três estereoisômeros para tais compostos, um par de enantiômeros e um composto meso.

A configuração do produto de adição depende da configuração do but-2-eno, que pode ser cis ou trans, e da estereoquímica da reação de adição via anti que ocorre na segunda etapa. O bromo é adicionado ao cis-but-2-eno para dar uma mistura enatiométrica (2R, 3R) - e (2S, 3S) - dibromobutanos. Embora o íon bromônio possa se formar por ataque igualmente bem na parte superior ou inferior, vamos examinar o intermediário obtido do ataque na parte superior. O intermediário obtido no ataque ao fundo é o mesmo por ser aquiral. O ataque subsequente do íon brometo pode ocorrer no átomo de carbono direito ou esquerdo. O ataque ao átomo de carbono correto dá o isômero 2R, 3R. O ataque ao átomo de carbono esquerdo dá o isômero 2S, 3S. Ambas as vias de ataque são igualmente prováveis e o resultado é uma mistura racêmica.
Agora vamos considerar as consequências da formação do íon bromônio cíclico derivado do trans-but-2-eno seguido pelo ataque nucleofílico do íon brometo. O íon bromônio resulta do ataque no topo. O íon brometo ataca igualmente bem os átomos de carbono direito e esquerdo, dando origem às estruturas 2S, 3R e 2R, 3S, respectivamente. Este padrão corresponde a dois átomos de carbono com centros estereogênicos equivalentemente substituídos em uma molécula com um plano de simetria; assim, este isômero corresponde a um único composto meso.
Agora podemos aceitar com segurança o mecanismo de adição de bromo a alcenos porque ele concorda com os fatos experimentais. Mais uma vez, descobrimos que os reagentes aquirais - neste caso cis- ou trans-but-2-eno e bromo - sempre formam produtos opticamente inativos. Lembre-se: os produtos possuem dois centros estereogênicos; a reação produz uma mistura racêmica ou um composto meso.[54]


Reações que formam diastereoisômeros[editar | editar código-fonte]
No tópico anterior, foi abordado a formação de compostos com um ou dois centros estereogênicos a partir de reagentes aquirais. Agora, veremos o que acontece quando um segundo centro estereogênico se forma em uma molécula quiral. Diastereômeros podem se formar. Uma molécula com um centro estereogênico, designado AR, que forma um segundo centro estereogênico em B dentro da molécula, poderia resultar na formação de ARBR e ARBS. Lembrando que um único enantiômero se origina quando um centro estereogênico se forma em uma molécula em um ambiente quiral, como aquele fornecido por uma enzima. Da mesma forma, um centro de quiralidade em uma molécula deve afetar a estereoquímica do segundo sítio quando os diastereômeros se formam.
Na hidrogenação de um alceno usando como catalisador um metal de transição, a molécula plana se liga à superfície do metal. Se o alceno for aquiral, o lado apresentado à superfície do metal não é importante. O alceno pode ser hidrogenado por cima ou por baixo para dar o produto hidrogenado. Se o alceno contém um átomo de carbono com centro estereogênico perto da ligação dupla, no entanto, dois produtos são possíveis. Considere a hidrogenação catalítica de (R)-1-metil-2-metilideciclohexano. Dois estereoisômeros, 1S, 2R e 1R, 2R, se formam, mas em quantidades desiguais. Aproximadamente 70% do produto é o isômero cis (1S, 2R).
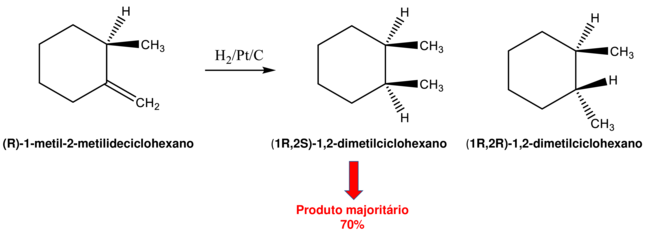
Como o alceno é quiral, há uma diferença entre o ambiente estérico das duas faces da ligação dupla. O grupo metil acima do plano diminui a probabilidade de hidrogenação daquela face da ligação dupla. A hidrogenação do lado inferior menos impedido empurra o grupo metil recém-formado para cima resultando na formação do isômero cis. Os dois estereoisômeros se formam em quantidades desiguais como consequência do centro estereogênico. A reação é estereoseletiva.
Observações semelhantes mostram que um enantiômero reage com um reagente aquiral para dar quantidades desiguais de produtos diastereoméricos. Os rendimentos relativos dos diastereoisômeros frequentemente dependem da estrutura do centro estereogênico existente e sua proximidade com o centro estereogênico recém-formado. Muitos centros estereogênicos estão presentes em um catalisador enzimático. Eles criam um ambiente quiral, o que leva a uma alta estereoseletividade. Normalmente, apenas um diatereoisômero se forma nas reações catalisadas por enzimas.[54]
Centros pró-quirais[editar | editar código-fonte]
Um centro atômico que pode se tornar quiral como resultado de uma reação estereoespecífica é chamado de pró-quiral. O grupo metileno do etanol fornece um exemplo simples. Como o átomo de carbono está ligado a dois átomos de hidrogênio, ele não é um centro estereogênico. Agora suponha que uma reação catalisada por uma enzima substitui um átomo de hidrogênio por um átomo de deutério. O resultado disso é a formação de dois enantiômeros. Os átomos de hidrogênio são enantiotópicos porque estão em um ambiente espelho-imagem. Designamos esses hidrogênios HR e HS. Por exemplo, compostos enantioméricos se formam se o deutério substitui um átomo de hidrogênio em C-1.

Os átomos ou grupos enantiotópicos são designados pro-R e pro-S. O átomo de hidrogênio atrás da página, como mostrado acima, é designado pró-S porque substituí-lo por deutério dá o enantiômero S.
O átomo de hidrogênio na frente da página é designado pró-R porque substituí-lo por deutério dá o enantiômero R. Um centro pró-quiral não pode ser convertido em um único composto quiral por um reagente simétrico (aquiral). No entanto, as enzimas que catalisam as reações bioquímicas são quirais. Portanto, as enzimas podem distinguir entre os grupos enantiotópicos de um centro pró quiral.
As enzimas têm locais de ligação específicos nos quais os substratos se encaixam. Para uma molécula como o etanol, quando os grupos CH3— e OH— se encaixam no local de ligação da enzima, os átomos de hidrogênio pró-quirais estão localizados em diferentes ambientes da enzima quiral. Uma reação pode ocorrer em um átomo de hidrogênio pró-quiral, por exemplo, e não no outro.
O conceito de pró-quiralidade também é importante para descrever as reações bioquímicas de moléculas que já possuem um ou mais centros quirais. A formação de um segundo centro quiral em um sítio aquiral pode levar a uma mistura de diastereoisômeros. Os dois grupos equivalentes no sítio aquiral são diastereotópicos.
Em seguida, consideramos uma reação em um átomo de carbono hibridizado sp2 ao ser convertido em um produto com um átomo de carbono hibridizado sp3. Embora o átomo de carbono trigonal de um grupo carbonila não seja um centro estereogênico, reduzir esse grupo a um álcool dá um novo centro estereogênico. Considere a formação de uma ligação C-H na redução do acetaldeído que foi deuterado em C-1. A formação de uma ligação em uma face dá um enantiômero; a formação de uma ligação C-H na face oposta dá o outro enantiômero.[54]

Para descrever as reações de adição nas duas faces possíveis das partes planas de uma molécula, devemos ser capazes de distinguir as faces. Para fazer isso, considere a sequência de grupos ligados ao átomo de carbono trigonal. Se, quando vistos de uma face, os grupos estão em uma sequência no sentido horário quando organizados pelas regras de prioridade R,S, essa face é designada re. Se a sequência de grupos é no sentido anti-horário, a face é designada si. Vendo o acetaldeído deuterado de cima da página, como mostrado anteriormente, a face é si porque a ordem dos grupos O>CH3> D é no sentido anti-horário. Se um hidrogênio adiciona à face Si, empurrando o deutério para baixo, o produto é (R)-(1-²H1)etanol.[54]

Etapa 8: Estudo Computacional da Reação[editar | editar código-fonte]
A química teórica e computacional pode fornecer grandes pistas sobre a validade ou não de uma proposta de mecanismo. Conhecer como os reagentes se transformam em produtos é inferir sobre a coordenada de reação e sobre a taxa com que os reagentes atravessam a barreira no sentido dos produtos. A principal estratégia para obter tais informações é fazendo uso da Teoria do Estado de Transição (TET). Porém, ela nos motiva a fazer melhor. Pode haver mais de um caminho e mais de uma barreira para se chegar até aos produtos, assim, para obter a taxa de reação geral, é preciso incluir nos cálculos esses vários caminhos. Para fazer isso computacionalmente, utilizam-se técnicas de dinâmica molecular (DM) ou suposições adicionais como feito da Teoria de Rice-Ramsperger-Kassel-Marcus (RRRM) que assume probabilidade de os produtos retornarem aos reagentes.[56]
Conceitos Básicos[editar | editar código-fonte]
Como já dito na Etapa 3, pode-se associar uma hipersuperfície que descreve as energias das moléculas como função da sua estrutura. Essa superfície multidimensional chamada de superfície de energia potencial (SEP) apresenta máximos, mínimos e pontos de sela (máximo ao longo de uma coordenada e mínimos em todas as outras). O primeiro passo para entender como essa superfície é construída está na aproximação de Born-Oppenheimer (ABO). A partir da separação do problema eletrônico do problema nuclear, podemos tratar a energia de interação entre os núcleos como na presença de um potencial efetivo gerado pelos elétrons. Todavia, mapear todas as energias para cada geometria possível é uma tarefa impossível, o que se faz, tipicamente, é variar as posições nucleares em algumas unidades e verificar a energia associada com a configuração. De forma mais prática ainda, os métodos computacionais modernos permitem determinar de forma bastante razoável qual deve ser conformação molecular no mínimo da superfície de energia potencial do estado fundamental, que é a estrutura que, em média, a molécula apresenta a maior parte do tempo em temperaturas ambientes.[57]
A energia é dada uma função escalar das coordenadas nucleares. Pode-se tomar seu gradiente e buscar a direção de mínimo, que será um ponto no qual o gradiente é nulo. Na verdade, o gradiente será zero em um máximo, mínimo ou um ponto de sela, cabendo as segundas derivadas a garantia de que temos um mínimo em um determinado ponto da superfície de energia potencial (SEP).[58] Se todas as segundas derivadas da energia são positivas tem-se um mínimo, e se apenas uma for negativa enquanto as outras são positivas, tem-se um ponto de sela. Esses são os pontos estacionários de interesse químico, pois o conhecimento dos pontos de mínimo dos reagentes é importante para busca do seus respectivos estados de transição. De longe, o método mais utilizado para otimizações de geometria e busca de pontos estacionários é o método de Newton-Raphson, mas existem muitos outros. Ele é interessante na busca de mínimos uma vez que converge linearmente para o mínimo no caso de uma função quadrática, que é aproximadamente o caso das distorções moleculares ao longo de uma coordenada vibracional.[59]
Em torno de um ponto de mínimo, pode-se fazer uma expansão em série de Taylor multidimensional da SEP da seguinte forma:
onde pode ser arbitrariamente escolhido como zero e como a primeira derivada em um mínimo é nula no mínimo, a equação se simplifica para:
Na qual F é a matriz das constantes de força (Hessiana) 3N x 3N para um sistema de N átomos, isto é, contém a segunda derivada da energia com respeito às coordenadas nucleares. A série é truncada no segundo termo e isso equivale considerar o problema dentro da aproximação harmônica, ou seja, cada vibração molecular deve se comportar aproximadamente como um oscilador harmônico.[57][58]
A equação de Schrödinger nuclear para um sistema de N átomos poderá ser escrita do seguinte modo:
Aqui é conveniente introduzir coordenadas ponderadas pela massa através das seguintes definições:
A equação de Schrödinger se modifica então para:
Pode-se realizar uma transformação unitária nas coordenadas y:
de modo que essa transformação a diagonaliza a matriz , produzindo autovalores com autovetores associados. Dessa forma, a equação de Schrödinger é agora:

O sistema de coordenadas q, isto é, aquele no qual a matriz Hessiana é diagonal, é chamado sistema de coordenadas normais. Nesse contexto, a eq. de Schrödinger 3N-dimensional é substituída por 3N equações de Schrödinger unidimensionais que nada mais são do que o problema do oscilador harmônico, cujas soluções do problema quântico são bem conhecidas como sendo polinômios de Hermite e que, nesse contexto, estão representados em termos das coordenadas normais de vibração. Além disso, as frequências associadas com cada um dos modos normais de cada um dos 3N osciladores é dada como tipicamente por:
Em geral, uma molécula com N átomos contém 3N-6 modos vibracionais, ou seja, são descontados os modos translacionais e rotacionais. Por essa razão, seis dos autovalores da Hessiana serão naturalmente nulos, ou pelo menos desprezíveis dentro das considerações numéricas dos cálculos.[57] Além disso, os cálculos de otimização são, em geral, realizados utilizando um sistema de coordenadas internas com a chamada matriz-z que acelera bastante os cálculos. A matriz-z nada mais é do que a descrição de um molécula em termos das distâncias, ângulos e diedros das ligações a partir de um átomo de referência.[60] Por exemplo, a matriz-z para água se escreve da seguinte forma em angstroms[61]:
H O 0.958 H 0.958 104.48
Quando a matriz Hessiana é calculada em um ponto de mínimo, seus autovalores são todos não-negativos. Porém, se a Hessiana é calculada sobre um ponto de sela (que pode servir para caracterizar o estado de transição), somente um de seu autovalores será negativo. Nessa situação, como pode-se notar pela equação acima, a frequência de vibração associada assume um valor imaginário (número negativo dentro da raiz). É possível se pensar na coordenada de reação como sendo aquela que está associada ao autovetor (modo normal de vibração do sistema) com autovalor imaginário. Essa caracterização é muito importante no estudo teórico das reações, pois com ela pode-se tomar etapas na direção de maior decréscimo de energia com o uso do gradiente da SEP e buscar os mínimos mais próximos. Contudo, para isto, é preciso garantir que o estado de transição obtido conecta os mínimos de interesse para reação, isso é, os reagentes e os produtos. O caminho de menor energia (CME) que conecta esses pontos estacionários em coordenadas ponderadas pela massa é chamado de coordenada intrínseca de reação (CIR). Existem vários métodos para determinação da CIR e usos distintos descritos na literatura.[57][62]
Deve-se destacar que a teoria do estado de transição não é uma teoria puramente quântica, mas semi-clássica onde a natureza quântica é atribuída a partir da quantização dos grau de liberdade translacionais, vibracionais e rotacionais de uma molécula. Além disso, em geral, cálculos quânticos fornecem a energia e os modos de vibração de uma ou algumas moléculas, por isso, para que os dados computacionais possam ser comparados com valores experimentais o emprego da mecânica estatística se torna essencial para fazer a ponte entre os dados microscópicos e macroscópicos. Por exemplo, para reação genérica:
a constante cinética é dada como pela lei de velocidades como:
Em nível microscópico a constante é uma função dos números quânticos que caracterizam os estados eletrônicos, translacionais, vibracionais e rotacionais de A, B e P. A constante cinética microscópica para sistemas em equilíbrio é então uma média ponderada dos estados termicamente acessíveis desses estados, o que se traduz pela distribuição de Boltzmann como sendo uma função da temperatura. Além disso, da equação de Eyring tem-se que a constante cinética é dada por:
onde , permite a obtenção de uma expressão para constante de equilíbrio pela razão das constante cinéticas da reação direta e inversa:
no presente contexto, as função termodinâmicas G, e consequentemente H e S, são calculadas a com a aplicação da mecânica estatística nos cálculos quânticos como será discutido em maiores detalhes adiante.
Por fim, cabe mencionar que o desenvolvimento feito aqui é restrito para o estudo de uma reação que ocorre ao longo de uma única SEP, o que é comum para as reações térmicas. Contudo, a existências das reações fotoquímicas aponta que isso é claramente uma limitação da descrição, uma vez que essas acontecem com a participação de ao menos duas SEPs associadas a estados eletrônicos distintos. Quando uma molécula absorve um fóton e segue para um estado excitado, a geometria que ela tinha antes é preservada inicialmente, mas raramente é um mínimo na SEP do estado excitado. A molécula pode retornar ao estado fundamental de várias maneiras, como por vias radiativas (Fluorescência e Fosforescência) ou por transições não-radiativas onde o excesso energético é dissipado através de vibrações no estado fundamental ou colisões. Para que as transições não-radiativas ocorram é necessário que a diferença de energia entre as superfícies não seja muito grande, tornando a transição mais provável. Em geral, as transições não-radiativas tendem a ocorrem em pontos nos quais as SEPs do estado fundamental e excitado se cruzam ou se aproximam muito uma da outra. Esse pontos são conhecidos como interseções cônicas e são muitas vezes o limitante para que uma reação ocorra, pois pode ser pouco provável que a molécula no estado excitado alcance a configuração da interseção cônica antes de retornar ao estado excitado.[57]
Busca do Estado de Transição[editar | editar código-fonte]
A busca por estados de transição é muito mais complexa que encontrar pontos estacionários na SEP. Na verdade, não há nenhuma garantia (matemática formal) de que irá funcionar. As várias metodologias utilizadas na busca de estados de transição podem ser divididas em dois grupos, (1) as baseadas na interpolação entre dois mínimos e (2) aquelas que usam informações locais. Os métodos que utilizam a interpolação partem em geral do conhecimento dos mínimos dos reagentes e dos produtos e buscam um estado de transição (ET) entre uma coordenada de reação que os conecta. Os métodos locais por outro lado, propagam as geometrias a partir do conhecimento somente da SEP em um ponto e possivelmente suas duas primeiras derivadas, por isso, boas estimativas do estado de transição são necessárias para a convergência do cálculo.[57]

De forma geral, varrer a SEP do sistema em busca de pontos estacionários é uma estratégia muito demorada e custosa computacionalmente. Programas de cálculos modernos, costumam buscar os estados de transição usando algoritmos baseados no método de Newton-Raphson, onde a energia pode ser maximizada com respeito a um modo de vibração do sistema e minimizado com respeito aos outros 3N-7 modos de vibrações restantes, que correspondem às outras autofunções da Hessiana. Contudo, essa estratégia depende de bons palpites iniciais da estrutura do estado de transição. Se há dificuldade para o algoritmo achar um ET e nenhum insight químico sobre como deve ser a estrutura do ET pode ser traçado, os programas de cálculo costumam ter recursos para fazer uma busca relaxada ao longo da SEP do sistema, ou seja, uma investigação da SEP de forma menos custosa (com o uso de métodos de cálculo pouco precisos e conjuntos de funções de bases menores) em busca de um ponto de sela que represente possivelmente o ET buscado.[57][63]
Além disso, uma vez conhecido um ET é de interesse central saber se de fato ele é o ponto de sela adequado que conecta dos reagentes e os produtos da reação investigada. O caminho de reação pode ser estimado utilizando a CIR, que nada mais é do que um método que aplica a estratégia de gradiente descendente para os intermediários mais próximos, sendo portanto, caso particular dos métodos de CME. Os métodos de CIR são bastante úteis na validação de se um estado de transição está mesmo relacionado aos reagentes e produtos.[57][64]

O Nudged Elastic Band (NEB) é também um método de busca do caminho de menor energia que relaciona mínimos em uma SEP. Quando a reação é mais complexa, pode não ser realístico pensar no estado de transição como se sucedendo ao longo de um modo de vibração do sistema. O uso mais comum do NEB é visando encontrar o ET mais energético em uma SEP.[63] No NEB um caminho de reação inicial é gerado e representado por um conjunto de configurações discretas dos átomos chamadas de imagens do sistema. Essas imagens são conectadas por "molas" virtuais de constante de força k e esse conjunto é chamado de banda elástica. O método NEB define uma função (chamada banda elástica) que é a soma das energias de todas as imagens e um termo com as constantes para distribuir as imagens ao longo do caminho. O método funciona minimizando a função, ou seja, minimizando todas as imagens ao longo do caminho da reação. Cada uma das imagens encontra sua configuração de energia mais baixa possível. Esta otimização restrita é feita adicionando a cada etapa constantes de força ao longo da banda entre as imagens, evitando assim que as imagens caminhem para o mínimo dos reagentes e produtos, e, ainda, garante que elas fiquem uniformemente distribuídas ao longo do caminho da reação e projetando o componente da força devido ao potencial perpendicular à função, isto é, a cada etapa dos cálculos as forças paralelas ao caminho de reação são eliminadas e que só as componentes perpendiculares da força contribuam para otimização.[57][63][65]
Uso da Mecânica Estatística na Cinética Química[editar | editar código-fonte]
Agora que já foram tratadas formas de se obter as configurações energéticas dos reagentes e produtos, do estado de transição e o caminho da reação, queremos fazer a ponte entre essas quantidades microscópicas para quantidades macroscopicamente mensuráveis. Isso é feito com o uso da mecânica estatística. Assim como o conhecimento da função de onda de um sistema quanto-mecânico é fundamental para o conhecimento de suas propriedades, a relação é análoga entre a função de partição q e os sistemas descritos pela mecânica estatística. A função de partição molecular fornece uma medida dos estados que são acessíveis a uma molécula para uma dada temperatura do sistema.[10]
Sabe-se do fator de Boltzmann que a probabilidade de um sistema estar num estado com energia é exponencialmente dependente da temperatura, de modo que:
Naturalmente, a soma de todas as probabilidades deve ser igual a 1, de modo que a constante de normalização para expressão acima é:
que é a chamada função de partição e a soma varre todos os estados. Dessa forma, a probabilidade do sistema estar em um estado j com energia é[1]:
Se a energia de uma molécula puder ser dada como uma soma das diferentes contribuições dos estados quânticos, ou seja, cada uma dos estados é independente do outro, então a energia da molécula i pode ser dada como:
onde os sobrescritos indicam as contribuições translacionais, rotacionais, vibracionais e eletrônicas, respectivamente. Essa expressão é aproximadamente verdadeira. Se a energia pode ser decomposta como uma soma de contribuições, a função de partição pode ser escrita como um produto das funções de partição translacionais, rotacionais, vibracionais e eletrônicas. Isso ocorre da seguinte forma:
A forma mais comum de modelar esse problema consiste em modelar a função de partição transicional como a função de partição do gás ideal, ou seja, não há interação entre as partículas; supor a função de partição vibracional como sendo a do oscilador harmônico, a rotacional como sendo a do rotor rígido e a eletrônica com a contribuição somente do estado fundamental (ou estados, caso haja degenerescência). Assim, a função de partição translacional é:
onde o único parâmetro molecular é a massa total M. O volume V depende do número de partículas e é comumente definido como o volume ocupado por um mol de gás ideal.
A função de partição vibracional é:
onde são as vibrações moleculares e a soma varre todos os 3N-6 modos de vibração de uma molécula poliatômica genérica, ou até 3N-7 se estivermos considerando um estado de transição, pois então, o modo de vibração imaginário associado a ele não é contabilizado.
A função de partição rotacional é dada por:
onde são os momentos de inercia e é o número de simetria da molécula considerada e representa o número de orientações indistinguíveis dela.
Para a função de partição eletrônica, a função de partição envolve vários estados que são as soluções da equação de Schrödinger eletrônica do problema molecular:
na qual indicam a degenerescência do estado, e só a estado fundamental é considerado como contribuinte para função de partição. É importante mencionar que o zero de energia é convencionado aqui como a energia molecular dos reagentes. Assim, a funções de partição para os reagentes e o estado de transição são dadas como:
onde é a diferença de energia entre os reagentes e o estado de transição.
As funções termodinâmicas podem ser calculadas a partir das seguintes expressões em termos da função de partição:
Aplicando essas equações nas funções de partição dos modelos adotados tem-se que as contribuições das funções termodinâmicas para o sistema são:
Para calcular utilizamos e . O valor de é dado simplesmente pela diferença da energia eletrônica dos reagentes e do ET. Além disso, com exceção de reações que envolvem vários estados eletrônicos, . Uma vez estimado o valor de pode-se utilizar a equação de Eyring para estimar as constantes cinéticas e também a de equilíbrio. Ademais, sem dúvidas, a maior contribuição para energia reacional provém do termo eletrônico, além desse ser o de maior dificuldade de ser estimar adequadamente.[56][57]
Para reações unimoleculares as contribuições de , e são zero, enquanto que não é necessariamente nulo, uma vez que as geometrias dos reagentes e do estado de transição podem ser diferentes, o que afetaria o termo que contém a raiz dos momentos de inércia. Pode-se mencionar ainda que a contribuição da variação de entalpia vibracional, , é levemente negativa, de poucos kJ/mol. A razão para isso é que há apenas um modo de vibração a menos, associado com o estado de transição. Além disso, estruturalmente, pode-se pensar no estado de transição como possuindo alguns modos de dissipação de energia a menos que os reagentes, o que é marcado num pequeno e negativo.
Para reações bimoleculares, ou seja, que dependem do encontro de duas moléculas de reagentes, e são constantes iguais a -4RT. Contudo, agora, e podem variar bastante, da ordem de -40 J/molK uma vez que existe o dobro de graus de liberdade translacional e rotacional nos reagentes em relação aos produtos, mas em contrapartida existem novos modos de vibração no ET que fazem e serem positivos em alguns poucos kJ/mol e J/molK, respectivamente. Nessas reações é comum ainda que a contribuição entrópica sozinha já é capaz de gerar uma barreira de cerca de 50 kj/mol em comparação com a contribuição eletrônica sozinha.
Como o método desenvolvido permite a obtenção das funções termodinâmicas dos reagentes, produtos e do estado de transição, é possível estimar o
da reação. Dessa forma, pode-se determinar os , e para reação, , e para o estado de transição, as constantes cinéticas k e as constantes de equilíbrio K. Todos esses parâmetros podem ser comparados com valores de referências experimentais, indicando se a modelagem do problema foi boa. Além disso, computacionalmente, esses parâmetros termodinâmicos e cinéticos para reação são obtidos supondo os isótopos mais comuns dos átomos envolvidos, mas eles podem ser considerados estatisticamente também para apresentar maior acordo experimental, ou ainda para previsão do efeitos dos isótopos sobre a cinética.
Por fim, se a reação pode ocorrer por múltiplos caminhos, a constante cinética observada experimentalmente pode ser comparada com a soma das constantes cinéticas sobre todos os caminhos:
a consequências de múltiplos caminhos reacionais com energias de ativação próximas dá origem a uma energia de ativação que é menor que a barreira energética do menor estado de transição.[57]
Uso da Dinâmica Molecular na Cinética Química[editar | editar código-fonte]

Os cálculos de otimização para obtenção dos mínimos e dos estados de transição são feitos considerando a temperatura como 0 K, onde todos os estados quânticos são os fundamentais. Com a mecânica estatística foi discutido como o efeito da temperatura pode ser tratado em parte nos sistemas químicos. Porém, o modelo de gases ideais, osciladores harmônicos e rotores rígidos supostos na construção da função de partição pode ser uma simplificação em demasia. Para levar em conta as moléculas se movem e interagem durante um processo químico e a relação dele com a temperatura, os método de dinâmica molecular são amplamente utilizados.[57] Em geral, referem-se aos métodos de dinâmica molecular (DM) como sendo aqueles há uma relação explicita entre o potencial de interação entre as partículas de um sistema e evoluem no tempo a com a aplicação de uma equação dinâmica a partir de um conjunto de coordenadas e velocidades iniciais. A equação dinâmica que trata do movimento dos núcleos num regime clássico e não relativístico é a equação de Newton, enquanto a equação dinâmica do tratamento quântico dos movimentos num regime também não relativístico é dado pela equação de Schrödinger. Chamam-se métodos de dinâmica molecular clássica aqueles que usam a eq. de Newton como eq. dinâmica para o deslocamentos dos núcleos. De forma, análoga, a dinâmica quântica é o nome dado ao método que usa da eq. de Schrödinger para incorporar o movimentos dos núcleos, podem assim contabilizar efeitos vibracionais e de tunelamento.
Dentro ainda da dinâmica molecular clássica, pode-se estar interessado, como é o caso, em fenômenos inerentemente quânticos como a quebra e formação de ligações, ou processos que envolvam mais de um estado eletrônico. Existem um conjunto de métodos que são capazes de contabilizar simultaneamente os efeitos quânticos das interações atômicas e a propagação dos núcleos e das velocidades de forma clássica resolvendo a eq. de Newton numericamente, esses métodos recebem o nome de Dinâmica Molecular Ab Initio (DMAI) ou Dinâmica Molecular Born-Oppenheimer (DMBO), pois tratam a função de onda eletrônica de forma quântica e os núcleos, separadamente, de forma clássica. Esses métodos precisam, em geral, de necessitam de uma função de onda bem convergida a cada etapa do calculo, o que é extremamente custos e consequentemente demorado. Dentre esses métodos destacam-se da Dinâmica Molecular Car-Parrinello, que supera parcialmente a necessidade de uma grande convergência da função de onda a cada etapa, pois os orbitais são otimizados simultaneamente com o movimento nuclear através da inclusão de parâmetros como massas fictícias na dinâmica. A Dinâmica Molecular Ab Initio GVB ("generalized valence bond", teoria da ligação de valência generalizada) é capaz de tratar corretamente as reações químicas, além de não ser tão custosa computacionalmente como outras técnicas disponíveis.[57][66][66]
No estudo de reações métodos híbridos são muito úteis combinando dinâmicas clássicas e quânticas, onde a dinâmica ao longo da coordenadas de reação é tratada de forma quântica, e nas outras regiões da SEP de forma clássica. A inclusão dos efeitos de dinâmica são muito importantes para fazer correções na teoria do estado de transição, em geral, sob a forma do coeficiente de transmissão . A dinâmica clássica permite que as correções devido as reações de volta, isso é, a dinâmica do equilíbrio, enquanto o tratamento quântico é essencial consideração de efeitos quânticos como o tunelamento. Se o estado de transição ou o caminho da reação são conhecidos, pode-se ainda amostrar configurações específicas na SEP como ponto de partida para dinâmica. De forma similar, as simulações de DM podem partir do estado de transição e a reação pode se suceder tanto no sentido dos produtos quantos dos reagentes. A amostragem dos estados de transição é interessante pois não necessita do conhecimento prévio da coordenada de reação e existem vários algoritmos que tratam desse problema.[57][67]
Exemplo de Mecanismo[editar | editar código-fonte]
Como exemplo consideramos a reação global entre o óxido nítrico e o oxigênio:
Se sabe que os produtos não se formam diretamente como resultado da colisão de duas moléculas NO com uma molécula de O2 porque se tenha encontrado a espécie N2O2 durante o curso da reação. Um mecanismo possível é supor que a reação se dá em duas etapas ou reações elementares como as seguintes:
- primeira etapa
- segunda etapa
Na primeira etapa duas moléculas de NO chocam-se para formar uma molécula de N2O2; é uma reação bimolecular. Depois, segue uma reação, entre o N2O2 e o O2 para formar duas moléculas de NO2; é uma reação bimolecular. A equação química global, que representa o câmbio total, se pode interpretar como a soma destas duas etapas.
As espécies como o N2O2 é o intermediário da reação.
Mecanismos de reação em Química Orgânica[editar | editar código-fonte]
A descrição das reações orgânicas permite o conhecimento de efeitos de temperatura, catalisadores e reações concorrentes. As reações orgânicas são classificadas em quatro grandes grupos: reações de substituição, reações de adição, reações de substituição e rearranjos moleculares.[68]
Alguns mecanismos são comuns a diversas reações. Os mecanismos SN1 e SN2 descrevem a maioria das substituições em carbonos alifáticos, a substituição eletrofílica aromática descreve a maioria das reações sobre o benzeno e derivados, a adição eletrofílica é comum a alcenos e alcinos, enquanto aldeídos e cetonas reagem na sua maioria por adições nucleofílicas e derivados de ácido carboxílico reagem por substituição acílica.[69] A formação de alcenos e outros compostos insaturados ocorre por mecanismos E1 e E2. O conhecimento destes mecanismos permite o reconhecimento de padrões de reação na Química orgânica.
Referências
- ↑ a b c d McQuarrie, Donald A. (1997). Physical chemistry : a molecular approach. John D. Simon. Sausalito, Calif.: [s.n.] OCLC 36292765
- ↑ a b Jonathan, Clayden (2001). Organic chemistry. [S.l.]: Oxford University Press. OCLC 43338068
- ↑ Houston, Paul L. (2006). Chemical kinetics and reaction dynamics. Mineola, New York: Dover Publications. OCLC 853678082
- ↑ «Convenções para setas curvas em química orgânica». Khan academy. Consultado em 25 de maio de 2023
- ↑ a b c Meek, Simon J.; Pitman, Catherine L.; Miller, Alexander J. M. (9 de fevereiro de 2016). «Deducing Reaction Mechanism: A Guide for Students, Researchers, and Instructors». Journal of Chemical Education (2): 275–286. ISSN 0021-9584. doi:10.1021/acs.jchemed.5b00160. Consultado em 27 de maio de 2021
- ↑ a b c d e f Carey, Francis A. (2007). Advanced organic chemistry. Richard J. Sundberg 5th ed ed. New York: Springer. OCLC 154040953
- ↑ Carey, Francis A. (2000). Química orgânica. Vol. 1 (7a. ed.). [S.l.]: Grupo A - AMGH. OCLC 923758602
- ↑ a b Smith, Michael, October 17- (2020). March's advanced organic chemistry : reactions, mechanisms, and structure. Jerry March Eighth edition ed. Hoboken, New Jersey: [s.n.] OCLC 1105737299
- ↑ «reaction rate | Facts & Formula». Encyclopædia Britannica (em inglês). Consultado em 10 de junho de 2021
- ↑ a b c d e f g h Atkins, P. W. (2018). Atkins' Physical chemistry. Julio De Paula, James Keeler Eleventh edition ed. Oxford, United Kingdom: [s.n.] OCLC 1020028162
- ↑ a b c d e f g h i j Anslyn, Eric V.; Dougherty, Dennis A. (2006). Modern physical organic chemistry. [S.l.]: University science books. ISBN 9781891389313
- ↑ a b Eyring, Henry (1 de fevereiro de 1935). «The Activated Complex in Chemical Reactions». The Journal of Chemical Physics (em inglês) (2): 107–115. ISSN 0021-9606. doi:10.1063/1.1749604. Consultado em 19 de fevereiro de 2024
- ↑ Evans, M. G.; Polanyi, M. (1935). «Some applications of the transition state method to the calculation of reaction velocities, especially in solution». Transactions of the Faraday Society (em inglês). 875 páginas. ISSN 0014-7672. doi:10.1039/tf9353100875. Consultado em 20 de fevereiro de 2024
- ↑ Gold, Victor, ed. (2019). The IUPAC Compendium of Chemical Terminology. Research Triangle Park, NC: International Union of Pure and Applied Chemistry (IUPAC)
- ↑ Bigeleisen, Jacob (1 de agosto de 1949). «The Relative Reaction Velocities of Isotopic Molecules». The Journal of Chemical Physics (8): 675–678. ISSN 0021-9606. doi:10.1063/1.1747368. Consultado em 16 de junho de 2021
- ↑ Fraser, O. B. J. (1937). «Nickel as a Catalyst». Transactions of The Electrochemical Society (1). 425 páginas. ISSN 0096-4743. doi:10.1149/1.3498303. Consultado em 17 de junho de 2021
- ↑ Jones, William D. (1 de fevereiro de 2003). «Isotope Effects in C−H Bond Activation Reactions by Transition Metals». Accounts of Chemical Research (2): 140–146. ISSN 0001-4842. doi:10.1021/ar020148i. Consultado em 18 de junho de 2021
- ↑ Jones, William D.; Feher, Frank J. (1 de agosto de 1986). «Isotope effects in arene carbon-hydrogen bond activation by [(C5Me5)Rh(PMe3)]». Journal of the American Chemical Society (16): 4814–4819. ISSN 0002-7863. doi:10.1021/ja00276a019. Consultado em 18 de junho de 2021
- ↑ Bercaw, John E.; Chen, George S.; Labinger, Jay A.; Lin, Bo-Lin (31 de dezembro de 2008). «Hydrogen Tunneling in Protonolysis of Platinum(II) and Palladium(II) Methyl Complexes: Mechanistic Implications». Journal of the American Chemical Society (52): 17654–17655. ISSN 0002-7863. doi:10.1021/ja807427d. Consultado em 18 de junho de 2021
- ↑ Cha, Y; Murray, C.; Klinman, J. (10 de março de 1989). «Hydrogen tunneling in enzyme reactions». Science (em inglês) (4896): 1325–1330. ISSN 0036-8075. doi:10.1126/science.2646716. Consultado em 18 de junho de 2021
- ↑ Meek, Simon J.; Pitman, Catherine L.; Miller, Alexander J. M. (9 de fevereiro de 2016). «Deducing Reaction Mechanism: A Guide for Students, Researchers, and Instructors». Journal of Chemical Education (em inglês) (2): 275–286. ISSN 0021-9584. doi:10.1021/acs.jchemed.5b00160. Consultado em 18 de junho de 2021
- ↑ Simmons, Eric M.; Hartwig, John F. (2012). «On the Interpretation of Deuterium Kinetic Isotope Effects in CH Bond Functionalizations by Transition-Metal Complexes». Angewandte Chemie International Edition (13): 3066–3072. ISSN 1521-3773. doi:10.1002/anie.201107334
- ↑ Brown, Seth N.; Myers, Andrew W.; Fulton, J. Robin; Mayer, James M. (1 de julho de 1998). «On the Mechanism of C−H Bond Activation in the Photochemical Arylation of Rhenium(V) Oxo Iodide Complexes». Organometallics (15): 3364–3374. ISSN 0276-7333. doi:10.1021/om980216y. Consultado em 18 de junho de 2021
- ↑ Kundu, Sabuj; Choi, Jongwook; Wang, David Y.; Choliy, Yuriy; Emge, Thomas J.; Krogh-Jespersen, Karsten; Goldman, Alan S. (3 de abril de 2013). «Cleavage of Ether, Ester, and Tosylate C(sp3)–O Bonds by an Iridium Complex, Initiated by Oxidative Addition of C–H Bonds. Experimental and Computational Studies». Journal of the American Chemical Society (13): 5127–5143. ISSN 0002-7863. doi:10.1021/ja312464b. Consultado em 18 de junho de 2021
- ↑ Singleton, Daniel A.; Thomas, Allen A. (1 de setembro de 1995). «High-Precision Simultaneous Determination of Multiple Small Kinetic Isotope Effects at Natural Abundance». Journal of the American Chemical Society (36): 9357–9358. ISSN 0002-7863. doi:10.1021/ja00141a030. Consultado em 21 de junho de 2021
- ↑ Singleton, Daniel A.; Szymanski, Michael J. (1 de outubro de 1999). «Simultaneous Determination of Intermolecular and Intramolecular 13C and 2H Kinetic Isotope Effects at Natural Abundance». Journal of the American Chemical Society (40): 9455–9456. ISSN 0002-7863. doi:10.1021/ja992016z. Consultado em 21 de junho de 2021
- ↑ «Donald J. Cram». www.nasonline.org. Consultado em 21 de junho de 2021
- ↑ Logan, S. R. «The origin and status of the Arrhenius equation.». Journal of Chemical Education, 1982; 59(4), 279 – 281
- ↑ a b Eyring, H. «The Activated Complex in Chemical Reactions.». The Journal of Chemical Physics, 1935; 3(2), 107 –115. doi:10.1063/1.1749604
- ↑ Zewail, A.H. «The birth of molecules.». Scientific American, 1990; 263(6), 40–46. doi:10.1142/9789814287609_0006
- ↑ a b c Hammett, L. P. «The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives». Journal of the American Chemical Society,1937; 59(1), 96–103. doi:10.1021/ja01280a022
- ↑ a b c d Lowry, Thomas H.; Richardson, Kathleen Schueller (1987). «2». Mechanism and Theory in Organic Chemistry, 3 Ed. [S.l.]: Benjamin Cummings Publishing Company
- ↑ Bronsted, J. N. (1928). «Acid and Basic Catalysis.». Chemical Reviews 5(3): 231–338. doi:10.1021/cr60019a001
- ↑ Hammett, L. P. (1935). «Some Relations between Reaction Rates and Equilibrium Constants». Chemical Reviews,17(1): 125–136. doi:10.1021/cr60056a010
- ↑ Hammett, L. P. (1940). Physical Organic Chemistry. New York, NY: McGraw-Hill Book Co. Inc.
- ↑ a b c d e Johnson, C.D. (1973). The Hammett Equation. London: Cambridge University Press
- ↑ Okamoto, Y., Inukai, T., & Brown, H. C. (1958). «Rates of Solvolysis of Phenyldimethylcarbinyl Chlorides Containing Meta Directing Substituents1,2.». Journal of the American Chemical Society, 80(18),: 4969–4972. doi:10.1021/ja01551a052
- ↑ Jaffe, H. H. (1953). «A Reëxamination of the Hammett Equation». Chemical Reviews, 53(2): 191–261. doi:10.1021/cr60165a003
- ↑ Hollingsworth, C. A., Seybold, P. G., & Hadad, C. M. (2002). «Substituent effects on the electronic structure and pKa of benzoic acid». International Journal of Quantum Chemistry, 90(4-5),: 1396–1403. doi:10.1002/qua.10362
- ↑ a b c «Relações Lineares de Energia Livre e Atividade Farmacológica - Parte I - Equação de Hammett». Bastos-Ceneviva, M. P. Quim. Nova, 7(3): 141-150 1984
- ↑ a b Brown, H. C., & Okamoto, Y. (1958). «Electrophilic Substituent Constants». Journal of the American Chemical Society, 80(18): 4979–4987. doi:10.1021/ja01551a055
- ↑ Chapman, N. B., Shorter, J. (1978). Correlation Analysis in Chemistry Recent Advances, 1 Ed. USA: Springer
- ↑ Tsuno, Y., & Fujio, M. «Varying resonance demand in carbocationic systems.». Chemical Society Reviews, 25(2): 129-139. doi:10.1039/cs9962500129
- ↑ Swain, C. G., & Lupton, E. C. (1968). «Field and resonance components of substitent effects». Journal of the American Chemical Society, 90(16): 4328–4337. doi:10.1021/ja01018a024
- ↑ Swain, C. G., Unger, S. H., Rosenquist, N. R., & Swain, M. S. (1983). «Substituent effects on chemical reactivity. Improved evaluation of field and resonance components». Journal of the American Chemical Society, 105(3): 492–502. doi:10.1021/ja00341a032
- ↑ Taft, R. W., & Lewis, I. C. «The General Applicability of a Fixed Scale of Inductive Effects. II. Inductive Effects of Dipolar Substituents in the Reactivities of m- and p-Substituted Derivatives of Benzene». Journal of the American Chemical Society, 80(10): 2436–2443. doi:10.1021/ja01543a023
- ↑ Topsom, R. D. (1983). «Contribution of theoretical chemistry to an understanding of electronic substituent effects.». Accounts of Chemical Research, 16(8): 292–298. doi:10.1021/ar00092a005
- ↑ Taft, R. W. (1952). «Linear Free Energy Relationships from Rates of Esterification and Hydrolysis of Aliphatic and Ortho-substituted Benzoate Esters.». Journal of the American Chemical Society, 74(11): 2729–2732. doi:10.1021/ja01131a010
- ↑ Taft, R. W. (1952). «Polar and Steric Substituent Constants for Aliphatic and o-Benzoate Groups from Rates of Esterification and Hydrolysis of Esters». Journal of the American Chemical Society, 74(12): 3120–3128. doi:10.1021/ja01132a049
- ↑ a b Carroll, Felix A. (2010). Perspectives on structure and mechanism in organic chemistry, 2 Ed. Hoboken, New Jersey: John Wiley & Sons, Inc.
- ↑ Taft, R. W. (1953). «The General Nature of the Proportionality of Polar Effects of Substituent Groups in Organic Chemistry.». Journal of the American Chemical Society, 75(17): 4231–4238. doi:10.1021/ja01113a027
- ↑ a b c d e f g h Autor., Singh, Maya Shankar (1960- ). (2014). Reactive intermediates in organic chemistry : structure, mechanism, and reactions. [S.l.]: Wiley-VCH Verlag GMbH & C. KGaA. OCLC 1129876874
- ↑ Drayer, Dennis E. (janeiro de 2001). «THE EARLY HISTORY OF STEREOCHEMISTRY: FROM THE DISCOVERY OF MOLECULAR ASYMMETRY AND THE FIRST RESOLUTION OF A RACEMATE BY PASTEUR TO THE ASYMMETRICAL CHIRAL CARBON OF VAN'T HOFF AND LE BEL*». Clinical Research and Regulatory Affairs (em inglês) (3): 181–203. ISSN 1060-1333. doi:10.1081/CRP-100108172. Consultado em 15 de junho de 2021
- ↑ a b c d e f g h i Ouellette, Robert J.; Rawn, J. David (2018). «Stereochemistry». Elsevier (em inglês): 213–253. ISBN 978-0-12-812838-1. doi:10.1016/b978-0-12-812838-1.50008-6. Consultado em 15 de junho de 2021
- ↑ «4.5. Stereochemistry of reactions | Organic Chemistry 1: An open textbook». courses.lumenlearning.com. Consultado em 15 de junho de 2021
- ↑ a b Levine, Raphael D. (13 de janeiro de 2005). Molecular Reaction Dynamics. [S.l.]: Cambridge University Press
- ↑ a b c d e f g h i j k l m n Frank., Jensen, (2006). Introduction to computational chemistry. [S.l.]: John Wiley & Sons. OCLC 804076136
- ↑ a b Attila., Szabo, (2012). Modern Quantum Chemistry : Introduction to Advanced Electronic Structure Theory. [S.l.]: Dover Publications. OCLC 868272681
- ↑ Nocedal, Jorge; Wright, Stephen J., eds. (1999). «Numerical Optimization». Springer Series in Operations Research and Financial Engineering. doi:10.1007/b98874. Consultado em 30 de maio de 2021
- ↑ Schlegel, H. Bernhard (14 de março de 1992). «A comparison of geometry optimization with internal, cartesian, and mixed coordinates». International Journal of Quantum Chemistry (S26): 243–252. ISSN 0020-7608. doi:10.1002/qua.560440821. Consultado em 30 de maio de 2021
- ↑ «CCCBDB listing of experimental geometry data page 2». cccbdb.nist.gov. Consultado em 30 de maio de 2021
- ↑ Michalak, Artur; Ziegler, Tom (1 de maio de 2001). «First-Principle Molecular Dynamic Simulations along the Intrinsic Reaction Paths». The Journal of Physical Chemistry A (em inglês) (17): 4333–4343. ISSN 1089-5639. doi:10.1021/jp0041297. Consultado em 30 de maio de 2021
- ↑ a b c Neese, Frank (17 de julho de 2017). «Software update: the ORCA program system, version 4.0. ORCA, version 4.2.1. Manual at orcaforum.kofo.mpg.de/». WIREs Computational Molecular Science (1). ISSN 1759-0876. doi:10.1002/wcms.1327. Consultado em 30 de maio de 2021
- ↑ R., Leach, Andrew (2009). Molecular modelling : principles and applications. [S.l.]: Pearson/Prentice Hall. OCLC 837238261
- ↑ Henkelman, Graeme; Uberuaga, Blas P.; Jónsson, Hannes (8 de dezembro de 2000). «A climbing image nudged elastic band method for finding saddle points and minimum energy paths». The Journal of Chemical Physics (em inglês) (22): 9901–9904. ISSN 0021-9606. doi:10.1063/1.1329672. Consultado em 30 de maio de 2021
- ↑ a b Gibson, Douglas A.; Ionova, Irina V.; Carter, Emily A. (junho de 1995). «A comparison of Car—Parrinello and Born—Oppenheimer generalized valence bond molecular dynamics». Chemical Physics Letters (em inglês) (4): 261–267. doi:10.1016/0009-2614(95)00537-E. Consultado em 2 de junho de 2021
- ↑ Mullen, Ryan Gotchy; Shea, Joan-Emma; Peters, Baron (9 de junho de 2015). «Easy Transition Path Sampling Methods: Flexible-Length Aimless Shooting and Permutation Shooting». Journal of Chemical Theory and Computation (em inglês) (6): 2421–2428. ISSN 1549-9618. doi:10.1021/acs.jctc.5b00032. Consultado em 3 de junho de 2021
- ↑ Fundamentos de Química Orgânica - Ciências da Vida e Saúde, Márcio Lazzarotto (ebook )
- ↑ Química Orgânica Vol. 1: Volume 1, 2012, Craig B. Fryhle, T. W. Graham Solomons






![{\displaystyle v=-{d[A] \over dt}={d[B] \over dt}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a70f33ffd5d04b9caae75e549428163122d965ed)
![{\displaystyle v=-{d[A] \over dt}\propto [A]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a091152459520cd5028517d1fecc84b05a2b60b5)
![{\displaystyle v=k[A]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d92c334b2c8f53c4e883ccf85046d4bd407c0abd)
![{\displaystyle \log v=\log k+n\log[A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82360e346735729c2faa6c151ff94214cc835ac0)

![{\displaystyle v=k[A]^{n}[B]^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/763c376a0e7217d29ea9b8f6b27d45893278521b)
![{\displaystyle [B]\cong [B]_{0},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc91f204606b63801db7e653a3355fd916f9de3c)
![{\displaystyle v=k_{obs}[A]^{n};k_{obs}=k[B]^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91692577c32aa304231ed9a746f5bc5c9a2f2375)
![{\displaystyle \ln[A]=\ln[A]_{0}-kt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2c797eb37692eae0af26b99008403c899e079fb)
![{\displaystyle {1 \over [A]}-{1 \over [A]_{0}}=kt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8cd0e661b79392a9f2f4d424d2e894d1d374926)
![{\displaystyle {[A]^{-n+1} \over -n+1}=-kt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/705200db61f4f841b778239f1c2641740b61c4d4)
![{\displaystyle \left({1 \over [B]_{0}-[A]_{0}}\right)\ln \left({[A]_{0}B \over [B]_{0}[A]}\right)=kt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1b31c71405bf1d98a992cb72e31ec8698a8bebf)
![{\displaystyle {\ce {A + B <=>[k_1][k_{-1}] I ->[k_2] P}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81f8f93c7db2898f4dcc7ff799316c632ea101db)



![{\displaystyle {d[P] \over dt}=k_{2}[I]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a06fc7d963c265775a440c5bfe9518fabedd3a3b)
![{\displaystyle {d[I] \over dt}=k_{1}[A][B]-k_{-1}[I]-k_{2}[I]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2042a0fbd0abccd4887508219555a49248b9682a)
![{\displaystyle k_{1}[A][B]-k_{-1}[I]-k_{2}[I]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c34e0fb00193288400c0e01410c46423c5cd98b7)
![{\displaystyle k_{1}[A][B]=k_{-1}[I]+k_{2}[I]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fe7e7846c399a3f53d3d0b868926a08af55c7cd)
![{\displaystyle [I]={k_{1}[A][B] \over k_{-1}+k_{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ece571fa63eaad5373b6094ea63a2e348a5cc02f)
![{\displaystyle {d[P] \over dt}=k_{2}{k_{1}[A][B] \over k_{-1}+k_{2}}={k_{1}k_{2} \over k_{-1}+k_{2}}[A][B]=k_{obs}[A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50010031bfaec372db6911c3067350f04c142c1a)

![{\displaystyle {d[P] \over dt}={k_{1}k_{2} \over k_{-1}+k_{2}}[A][B]\cong {k_{1}k_{2} \over k_{-1}}[A][B]=K_{eq}k_{2}[A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1efb6ebd295f0ef444a6cbe44189ec4b6953c673)

![{\displaystyle {d[P] \over dt}={k_{1}k_{2} \over k_{-1}+k_{2}}[A][B]\cong {k_{1}k_{2} \over k_{2}}[A][B]=k_{1}[A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2cf6aa1e0dfb7e6cf5b6d35cce1cb09978115d5)



![{\displaystyle P_{x}=[X]RT}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb461ff1622ea4ac3456d8e5fd67e3537706e8c3)
![{\displaystyle K^{\ddagger }={\frac {[C^{\ddagger }]RT}{[A]RT[B]RT}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d31895483b01e39b6b943fee0071fcceef360a7d)
![{\displaystyle [C^{\ddagger }]=RTK^{\ddagger }[A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2a5aad28ea80f426c547aa7a0fe0cdc3ee95cde)


![{\displaystyle v=k^{\ddagger }[C^{\ddagger }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/931d2b2cd688a422846d59cef8047ae52776e88e)
![{\displaystyle v=k^{\ddagger }RTK^{\ddagger }[A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6fda1dc0eb3e2b7595933b92136bdc5b3fbe531)

![{\displaystyle v=k_{r}[A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcd354b745dcf3c226be0353f1057d828af4cf60)

























![{\displaystyle \ln \left({\frac {k}{T}}\right)=\left[\ln \left({\frac {k_{b}}{h}}\right)+{\frac {\Delta S^{\ddagger }}{R}}\right]-{\frac {\Delta H^{\ddagger }}{R}}\left({\frac {1}{T}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e4412d73ca8ce6b0ba57e5289d4d0ffdf272fe5)





![{\displaystyle \Delta S^{\ddagger }=R\left[b-\ln \left({\frac {k_{b}}{h}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fc213977f122f2e9b66adbe657841b225c1bafe)





































![{\displaystyle KIE_{calc}={\frac {ln(1-F)}{ln[(1-F)R/Ro]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71bf929b91b5e69e50804fc6ccee1b5c870dce0b)



















































![{\displaystyle \left[\sum _{i=1}^{3N}\left(-{\frac {1}{2M_{i}}}{\frac {\partial ^{2}}{\partial x_{i}^{2}}}\right)+{\frac {1}{2}}\Delta \mathbf {x} ^{t}\mathbf {F} \Delta \mathbf {x} \right]\chi _{Nuc}=E_{Nuc}\chi _{Nuc}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c7017646fc0b9bc6dcf66a3c354ca03a5a8e62c)




![{\displaystyle \left[-\sum _{i=1}^{3N}\left({\frac {\partial ^{2}}{\partial y_{i}^{2}}}\right)+{\frac {1}{2}}\mathbf {y} ^{t}\mathbf {(} \mathbf {F\centerdot G} )\mathbf {y} \right]\chi _{Nuc}=E_{Nuc}\chi _{Nuc}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5345d1c682c6d45779ef54b72a1981b4c3f4dd87)





![{\displaystyle \left[-\sum _{i=1}^{3N}\left({\frac {\partial ^{2}}{\partial q_{i}^{2}}}\right)+{\frac {1}{2}}\mathbf {y} ^{t}\mathbf {\mathbf {U} } (\mathbf {F\centerdot G} )\mathbf {U^{t}} \mathbf {y} \right]\chi _{Nuc}=E_{Nuc}\chi _{Nuc}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c9cd9dd31f9e2a89a62ca666e23878e0823908b)
![{\displaystyle \left[-\sum _{i=1}^{3N}\left({\frac {\partial ^{2}}{\partial q_{i}^{2}}}+{\frac {1}{2}}\varepsilon _{i}q_{i}^{2}\right)\right]\chi _{Nuc}=E_{Nuc}\chi _{Nuc}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eed45b0383dd0fd3f14a5a7b57292440c552c990)


![{\displaystyle k[A][B]=-{\frac {d[A]}{dt}}=-{\frac {d[B]}{dt}}={\frac {d[P]}{dt}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a374a9f39246141f622e022887981a152869b53d)

































![{\displaystyle S_{T}={\frac {5}{2}}R+R\,ln\left[{\frac {V}{N_{A}}}\left({\frac {2\pi Mk_{B}T}{h^{2}}}\right)^{3/2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac63ee5ea49cc981c84415d6da16d92b3e00abc9)
![{\displaystyle S_{R}={\frac {3}{2}}R+R\,ln\left[{\frac {\sqrt {\pi }}{\sigma }}\left({\frac {8\pi ^{2}k_{B}T}{h^{2}}}\right)^{3/2}{\sqrt {I_{1}I_{2}I_{3}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2867207354ead847398c026adedfb5cd15d9396e)




















