Função afim


Uma função afim, também conhecida como função polinomial de grau 1 ou função polinomial de primeiro grau é uma função do tipo cujo gráfico é uma reta não perpendicular ao eixo Tal função também pode ser entendida como uma transformação linear () seguida por uma translação ().
no caso finito-dimensional cada função afim é dada por uma matriz A e por um vetor B, que possam ser escritos como a matriz A com uma coluna extra do B. Fisicamente, uma função afim é a que preserva:
- Colinearidade entre pontos, isto é, três pontos que se encontram em uma linha continuam a ser colineares após a transformação;
- relações das distâncias ao longo de uma linha, isto é, para os pontos colineares distintos ,
Uma função afim é composta de um ou de diversos transformadores lineares. Diversas transformações lineares podem ser combinadas em uma única matriz, assim que a fórmula geral dada acima é ainda aplicável.
Em uma dimensão (ou seja, quando x e y são escalares), os termos A e b são chamados, respectivamente, de coeficiente angular e coeficiente linear.
Definição formal[editar | editar código-fonte]
Uma função chama-se função afim quando existe dois números reais e tal que e para todo [1][2]
Coeficientes[3][editar | editar código-fonte]
Para facilitar a análise dessas funções, dizemos que o coeficiente "a" da função é o coeficiente angular ou declividade da reta. Esse coeficiente determina a tangente do ângulo da inclinação da reta que representa a função, no sentido anti-horário em relação do eixo das abcissas.
O coeficiente "b" determina o deslocamento da reta em relação à origem, por isso ele é conhecido como coeficiente linear da reta.

Função linear[editar | editar código-fonte]
Uma função linear é um caso particular da função afim onde e sendo, portanto, expressa como:
Veja na figura ao lado um exemplo de gráfico de função linear.
Um caso específico da função linear é a função identidade, onde Logo a função identidade é expressa como:
Observe na figura ao lado um exemplo de gráfico de função identidade.
Função linear e proporcionalidade[editar | editar código-fonte]

Uma das principais aplicações da função linear é a relação de proporção existente entre os elementos do domínio e da imagem, pois observamos que conforme variam os elementos do domínio, suas respectivas imagens variam na mesma proporção, sendo essa proporção o coeficiente angular da função, nesse caso chamado de taxa de variação.
Assim, seja a função linear vemos que o conjunto dos pontos que representa a reta dessa função são os pontos do tipo onde é a razão entre e [4]
Essa relação será diretamente proporcional se a função for crescente e inversamente proporcional se a função for decrescente.
Crescimento ou decrescimento[editar | editar código-fonte]
Uma função afim pode ser crescente, decrescente, dependendo do valor do coeficiente angular. Uma função pode ainda ser constante, se a=0 e aí ela terá grau 0.
Crescente[editar | editar código-fonte]
Uma função afim é crescente quando seu coeficiente angular for positivo, ou seja,
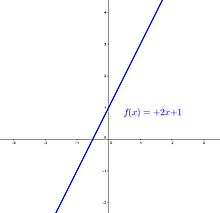
Demonstração: [5]
Por definição, dizemos que uma função definida por é crescente no conjunto se, para dois valores quaisquer e pertencentes a com tivermos
Sintetizando: é crescente quanto:
Podemos reescrever isso como:
Então, dada a função afim dizemos que é crescente se, e somente se:
Assim, podemos reescrever:
Decrescente[editar | editar código-fonte]

Uma função afim é decrescente quando seu coeficiente angular for negativo,ou seja,
Demonstração:[5]
De forma similar à função crescente, uma função é decrescente se obedecer à seguinte restrição:
Que é equivalente a dizer:
Então, dada a função afim dizemos que é decrescente quando:
Reescrevendo isso, temos:
Constante[editar | editar código-fonte]
Uma função é constante (neste caso dizemos que ela não é afim) quando seu coeficiente angular for nulo, ou seja Nesse caso a equação que define a função é dada por e seu gráfico é uma reta paralela ao eixo .

Zero[editar | editar código-fonte]
O zero de uma função afim (ou raízes da função) é o valor de para o qual a função é igual a zero. Geometricamente o zero de uma função afim é o ponto de corte no eixo das abcissas.
Para definir este ponto basta resolver a equação

Logo o ponto de corte no eixo das abcissas é
Toda e qualquer função afim também corta o eixo das ordenadas (eixo ). Para definir este ponto de corte basta calcular
Logo o ponto de corte no eixo y é
Aplicações[editar | editar código-fonte]
As funções afins possuem diversas aplicações, em situações que apresentam crescimento ou decrescimento linear.
Relação com a progressão aritmética[editar | editar código-fonte]
Uma progressão aritmética é uma sequência numérica em que cada termo, a partir do segundo, é igual à soma do termo anterior com uma constante.[6]
Logo, por ter essa característica, vemos que o crescimento de uma P.A é linear e pode, portanto, ser representado por uma função afim.
Para chegar até a função afim de uma P.A. partiremos da fórmula do termo geral, que é:
Como buscamos conhecer um termo em função da sua posição em uma P.A., podemos reescrever a fórmula como:
Temos, aplicando a propriedade distributiva e organizando os termos:

onde:
é a variável dependente; é a variável independente; é o coeficiente angular; é o coeficiente linear.
O domínio dessa função é o conjunto dos números naturais não nulos e a imagem é o conjunto dos números inteiros.
Exemplo:
Seja a progressão aritmética infinita vamos verificar se seus termos são definidos pela fórmula
Temos que e
Logo, a lei da função é:
Observe ao lado o gráfico da função
Relação com o movimento retilíneo uniforme[editar | editar código-fonte]
Situações que envolvem movimento em linha reta e com velocidade fixa podem ser estudadas utilizando funções afins. Para isso é preciso analisar a posição do objeto que se movimenta em função do tempo.
A física define a velocidade de um objeto como a razão entre a variação da distância pela variação do tempo, como observamos na fórmula abaixo:
,[8]
onde:
é a distância final; é a distância inicial; a distância final e a distância inicial.
Podemos simplificar a expressão, pois na maioria dos casos temos como ponto de partida um tempo inicial nulo,
Logo é possível modificar a expressão utilizando algebrismos para encontrar uma função afim de posição em função do tempo.
Podemos reescrever de modo a obter
Por fim basta renomear os termos para melhorar a lei da função. Assim dissemos que e
Logo a lei da função posição é:
,[9]
onde:
- é a posição após o tempo
- é a velocidade e o coeficiente angular da função;
- é o tempo que dura o deslocamento;
- é a posição inicial e também o coeficiente linear da função.
Veja também[editar | editar código-fonte]
Referências
- ↑ «Só Matemática, Função de Primeiro Grau». www.somatematica.com.br. Consultado em 29 de outubro de 2015
- ↑ Gelson., Iezzi, (2009). Fundamentos de matemática elementar, 1 : conjuntos, funções 7. ed. São Paulo (SP): Atual. ISBN 8535704558. OCLC 817124667
- ↑ Dante, Luiz Roberto (2005). Matemática, volume único. São Paulo: Ática. ISBN 9788508098019
- ↑ [1]
- ↑ a b Iezzi;, Gelson;; Murakami, Calor (2004). Fundamentos de Matemática Elementar 1, conjuntos, funções. [S.l.: s.n.] ISBN 978-85-357-0455-6
- ↑ Iezzi, Gelson; Hazzan, Samuel (2004). Fundamentos de Matemática Elementar 4. Sequências, matrizes, determinantes, sistemas. São Paulo: [s.n.] ISBN 9788535704587
- ↑ «Progressão Aritmética». InfoEscola. plus.google.com/+infoescola/. Consultado em 12 de novembro de 2015
- ↑ «Movimento Retilíneo Uniforme (MRU) - Física». InfoEscola. plus.google.com/+infoescola/. Consultado em 12 de novembro de 2015
- ↑ Dante, Luiz Roberto (2010). Matemática: Contexto e aplicações. [S.l.: s.n.] ISBN 9788508113002
Bibliografia[editar | editar código-fonte]
- Iezzi, Gelson; Murakami, Carlos. Fundamentos de Matemática Elementar,1: conjuntos, funções. 8. ed. São Paulo: Atual, 2004.




















































































