Prisma

Um prisma é o sólido geométrico formado pela união de todos os segmentos de reta congruentes e paralelos a um segmento dado, com uma extremidade nos pontos de um polígono fixo não paralelo a esse.[1] Ou seja, um prisma é um poliedro com duas faces congruentes e paralelas (bases) e cujas demais faces (faces laterais) são paralelogramos.[2][3] Os prismas são classificados de acordo com a forma de suas bases. Por exemplo, se temos pentágonos nas bases, teremos um prisma pentagonal. O prisma pode ser classificado em reto quando suas arestas laterais são perpendiculares aos planos das bases, e oblíquo quando não são.[4]
Definição[editar | editar código-fonte]
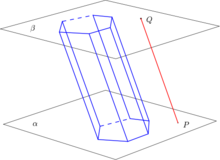
Um prisma (limitado) é o sólido geométrico formado pela união de todos os segmentos de reta congruentes e paralelos a um segmento dado (chamado de segmento de reta suporte), com uma extremidade nos pontos de um polígono fixo não paralelo a .[1] Desta forma, o sólido formado é um poliedro com duas faces congruentes e paralelas (chamadas de bases) e cujas demais faces (chamadas faces laterais) são paralelogramos.[2][3]
O termo prisma também pode significar prisma ilimitado, que é o sólido formado pela união de todas as retas paralelas a uma reta dada e que interceptam um polígono fixo não paralelo a .[1] Salvo menção, usaremos o termo prisma para significar um prisma limitado.
Elementos[editar | editar código-fonte]
Um prisma -poligonal é formado por duas bases congruentes e paralelas, faces laterais, diedros, arestas, triedros e vértices.[1] Em um espaço orientado, as bases são comumente classificadas em base inferior ou superior, conforme a orientação dada.[2]
Classificação[editar | editar código-fonte]

Os prismas são classificados conforme as propriedades dos polígonos que formam suas bases. Assim, prismas de bases convexas são chamados de prismas convexos. Prismas triangulares, quadrangulares, pentagonais, -poligonais, são aqueles cujas bases são triângulos, quadriláteros, pentágonos, polígonos com lados, respetivamente.[1]
Prismas quadrangulares seguem classificação específica. Um prisma cujas bases são paralelogramos é chamado de paralelepípedo.[3] Um paralelepípedo cujas arestas são todas congruentes entre si é chamado de romboedro.[1]
Os prismas também são classificados quanto ao ângulo que a reta suporte faz com os planos que contém suas bases. Ou seja, um prisma é dito ser oblíquo quando sua reta suporte faz um ângulo oblíquo com os planos das bases. É dito ser reto quando a reta suporte faz um ângulo reto com os planos das bases. Neste caso, as faces laterais são retângulos.[2] Especificamente, um romboedro reto cujas bases são retângulos é chamado cubo.[1]
Além disso, um prisma reto cujos polígonos das bases são regulares é chamado de prisma regular.[1]
Altura[editar | editar código-fonte]
A altura de um prisma é a distância entre suas bases.[1]Desta forma, observamos que a altura de um prisma reto é igual ao comprimento de qualquer uma de suas arestas laterais.
Área da superfície[editar | editar código-fonte]
A superfície (total) de um prisma é a união de todas as suas faces. A união apenas de suas faces laterais é chamada de superfície lateral. A área da superfície lateral é a soma das áreas de cada face lateral do prisma. A área da superfície total é dada por:
onde, é a área de qualquer uma das bases do prisma.[1]
Volume[editar | editar código-fonte]
O volume de um prisma é dado por[1][3]:
onde, é a área de qualquer uma de suas bases e é sua altura.
Ver também[editar | editar código-fonte]
Referências
- ↑ a b c d e f g h i j k Dolce, Osvaldo Pompeo (2013). Fundamentos de Matemática Elementar - Vol. 10 7 ed. [S.l.]: Atual. ISBN 9788535717587
- ↑ a b c d Weisstein, Eric W. «Prism -- from MathWorld --A Wolfram Web Resource». Consultado em 10 de novembro de 2014
- ↑ a b c d Lima, Elon Lages (2006). A matemática do ensino médio - volume 2 6 ed. [S.l.]: SBM. ISBN 8585818115
- ↑ Iezzi, Gelson; Dolce, Osvaldo; Degenszajn, David; Périgo, Roberto (2013). «10». Matemática. ciência e aplicações. 2 7 ed. São Paulo: Saraiva. p. 187. 320 páginas. ISBN 978-85-02-19426-7
Bibliografia[editar | editar código-fonte]
- Anthony Pugh (1976). Polyhedra: A visual approach (em inglês). Califórnia: University of California Press Berkeley. ISBN 0-520-03056-7












