Sage

Sage
Desenvolvedor	William Stein
Plataforma	Python
Lançado em	24 de fevereiro de 2005 (8 anos)
Versão estável	5.7 (19 de fevereiro de 2013)
Escrito em	Python, Cython
Sistema Operacional	Multiplataforma
Gênero(s)	Sistema algébrico computacional
Licença	GNU General Public License
Página oficial	http://www.sagemath.org/ (em inglês, em espanhol, em chinês, em francês, em alemão, em português e em russo) , acessado pela última vez há 56 semanas e 6 dias
Tamanho	411 MB - ficheiro de download (Ubuntu 64-bit)
Portal das Tecnologias de informação

O Sage (anteriormente SAGE, acrónimo em inglês para Sistema de Experimentações Geométricas e Algébricas ) é um software de matemática que possui recursos que abrangem muitas áreas da matemática, incluindo álgebra, combinatória, análise numérica, teoria dos números e cálculo. O Sage é por vezes chamado de sagemath, para o distinguir de outros usos da palavra.
A primeira versão do Sage foi lançada em 24 de fevereiro de 2005 como um software livre e de código aberto, nos termos da GNU General Public License, com o objectivo de criar uma "alternativa de código aberto à outros programas, como o Magma, Maple, Mathematica e MATLAB".
O Sage utiliza a linguagem de programação Python, suportando programações procedural, funcional e de orientação a objetos.

Características

A interface gráfica do Sage funciona como a maioria dos navegadores web

Resolução de equações e de diagramação utilizando a interface web do Sage

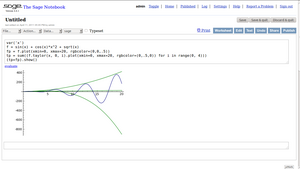
Entre as características do Sage, estão:

• Uma interface gráfica para revisão e reutilização de entradas e saídas anteriores, incluindo gráficos e anotações de texto. Compatível com os navegadores Firefox, Opera, Konqueror e Safari. Os notebooks podem ser acessados ​​localmente ou remotamente, e a conexão pode ser assegurada com HTTPS.
• Um interpretador de comandos baseado em texto usando IPython.
• Computação paralela, usando processadores multinúcleo, multiprocessamento simétrico e computação distribuída.
• Cálculo, usando Maxima e SymPy.
• Álgebra linear numérica, usando GSL, SciPy e NumPy.
• Bibliotecas de funções elementares e especiais.
• Gráficos 2D e 3D de funções simbólicas e dados numéricos.
• Manipulação de matrizes, incluindo matrizes esparsas.
• Bibliotecas de estatísticas multivariáveis, usando R e SciPy.
• Uma caixa de ferramentas para acrescentar interfaces do utilizador a cálculos e aplicações.
• Ferramentas para o processamento de imagens, usando pylab e Python.
• Ferramentas para visualizar e analisar gráficos.
• Bibliotecas para funções de teoria dos números.
• Filtros para importação e exportação de dados, imagens, vídeo, áudio, CAD e GIS.
• Suporte para números complexos, aritmética de precisão arbitrária e matemática simbólica, sempre que isto for apropriado.
• MoinMoin como um sistema Wiki, para gestão do conhecimento.
• Documentação, usando Sphinx.
• Interface para alguns softwares proprietários, como o Mathematica, Magma, R, e Maple.

Desenvolvimento

William Stein, desenvolvedor do Sage

William Stein percebeu, ao projectar o Sage, que já havia muitos softwares de código aberto escritos em diferentes linguagens de programação, a saber, C, C++, Common Lisp, Fortran e Python.
Ao invés de reinventar a roda, o Sage (que é escrito principalmente em Python e Cython) integra vários softwares de matemática em uma interface comum, para que um utilizador necessite saber apenas Python.
Tanto estudantes quanto profissionais auxiliam no desenvolvimento do Sage. O desenvolvimento do Sage é auxiliado por trabalhos voluntários e doações.

Histórico de lançamentos

Apenas os maiores lançamentos estão listados abaixo. O Sage segue o conceito "liberação antecipada e frequente", lançando novas versões com diferença de poucas semanas ou meses. No total, houve mais de 300 novas versões lançadas, embora a frequência de atualizações tenha diminuído.

Versão	Data de lançamento	Descrição
0.1	Janeiro de 2005	Inclui PARI, mas não GAP ou Singular
0.2 - 0.4	Março a Julho de 2005	Banco de dados do Cremona, polinômios multivariados, campos finitos grandes e mais documentação
0.5 - 0.7	Agosto e Setembro de 2005	Espaços vectoriais, anéis, símbolos modulares e janelas de utilização
0.8	Outubro de 2005	Distribuição completa do GAP, Singular
0.9	Novembro de 2005	Maxima e clisp adicionados
1.0	Fevereiro de 2006
2.0	Janeiro de 2007
3.0	Abril de 2008
4.0	Maio de 2009
5.0	Edição futura

Conquistas

Em 2007, o Sage ganhou o primeiro prémio na divisão de software científico do Les Trophées du Libre, uma competição internacional para software livre.
O Sage também já foi citado em várias publicações.

Licença e disponibilidade

O Sage é software livre, distribuído sob os termos da GNU General Public License, versão 2 ou posterior. O programa está disponível de várias maneiras:

• O código-fonte pode ser descarregado da página de downloads. Embora não recomendável para usuários finais, os lançamentos de versões beta do Sage também estão disponíveis.
• Pode-se descarregar binários para Linux, OS X e Solaris (x86 e SPARC).
• Um live CD contendo o sistema operacional inicializável Linux também está disponível. Isto permite a utilização do Sage sem a instalação do Linux.
• Os utilizadores podem utilizar uma versão online do Sage em sagenb.org ou http://t2nb.math.washington.edu:8080/, mas com um limite de quantidade de memória que um utilizador poderá usar.

Embora a Microsoft estava patrocinando uma versão nativa do Sage para o sistema operacional Windows , mas até 2012 não havia planos para o desenvolvimento de uma versão nativa, e os utilizadores do Windows têm actualmente que utilizar máquinas virtuais, como o VirtualBox, para poderem executar o Sage.
As distribuições Linux em que o Sage está disponível como um pacote são Mandriva e Arch Linux. O Sage pode ser instalado em qualquer distribuição Linux.

Pacotes de software contidos no Sage

A filosofia do Sage é a utilização de bibliotecas de softwares de código aberto, onde quer que existam. Por isso, utiliza muitas bibliotecas de outros projectos.

Pacotes de matemática contidos no Sage

Álgebra	GAP, Maxima, Singular, Macaulay 2
Geometria algébrica	Singular, Macaulay 2
Aritmética de precisão arbitrária	MPIR, MPFR, MPFI, NTL, mpmath
Geometria aritmética	PARI/GP, NTL, mwrank, ecm
Cálculo	Maxima, SymPy, GiNaC
Combinatória	Symmetrica, Sage-Combinat
Álgebra linear	ATLAS, BLAS, LAPACK, NumPy, LinBox, IML, GSL
Teoria dos gráficos	NetworkX
Teoria dos grupos	GAP
Computação numérica	GSL, SciPy, NumPy, ATLAS, Scilab, GNU_Octave
Teoria dos números	PARI/GP, FLINT, NTL, Kash/Kant
Computação estatística	R, SciPy

Outros pacotes contidos no Sage

Shell da linha de comando	IPython
Banco de dados	ZODB, Python pickles, SQLite
Configuração do tipo de matemática	LaTeX
Interface gráfica	Sage Notebook, jsmath
Gráficos	Matplotlib, Tachyon3d, GD, Jmol
Linguagem de programação interativa	Python
Rede	Twisted

Exemplos de utilização

Álgebra e cálculo

x, a, b, c = var('x, a, b, c')
 
log(sqrt(a)).simplify_log() # returns 1/2*log(a)
log(a / b).expand_log() # returns log(a) - log(b)
sin(a + b).simplify_trig() # returns sin(a)*cos(b) + sin(b)*cos(a)
cos(a + b).simplify_trig() # returns -sin(a)*sin(b) + cos(a)*cos(b)
(a + b)^5 # returns (a + b)^5
expand((a + b) ^ 5) # a^5 + 5*a^4*b + 10*a^3*b^2 + 10*a^2*b^3 + 5*a*b^4 + b^5
 
limit((x ^ 2 + 1) / (2 + x + 3 * x ^ 2), x=Infinity) # returns 1/3
limit(sin(x) / x, x=0) # returns 1
 
diff(acos(x), x) # returns -1/sqrt(-x^2 + 1)
f = exp(x) * log(x)
f.diff(x, 3) # returns e^x*log(x) + 3*e^x/x - 3*e^x/x^2 + 2*e^x/x^3
 
solve(a * x ^ 2 + b * x + c, x) # returns [x == -1/2*(b + sqrt(-4*a*c + b^2))/a, x == -1/2*(b - sqrt(-4*a*c + b^2))/a]
 
f = x ^ 2 + 432 / x
solve(f.diff(x) == 0, x) # returns [x == 3*I*sqrt(3) - 3, x == -3*I*sqrt(3) - 3, x == 6]

Equações diferenciais

t = var('t') # define a variable t
x = function('x', t) # define x to be a function of that variable
DE = lambda y: diff(y, t) + y - 1
desolve(DE(x(x=t)), [x, t]) # returns (c + e^t)*e^(-t)

Álgebra linear

A = Matrix([[1, 2, 3], [3, 2, 1], [1, 1, 1]])
y = vector([0, -4, -1])
A.solve_right(y) # returns (-2, 1, 0)
A.eigenvalues() # returns [5, 0, -1]
 
B = Matrix([[1, 2, 3], [3, 2, 1], [1, 2, 1]])
B.inverse() # returns
'''[   0  1/2 -1/2]
   [-1/4 -1/4    1]
   [ 1/2    0 -1/2]'''
 
# Call NumPy for the Moore-Penrose pseudo-inverse, since Sage does not support that yet.
 
import numpy
C = Matrix([[1 , 1], [2 , 2]])
matrix(numpy.linalg.pinv(C.numpy())) # returns
'''[0.1 0.2]
   [0.1 0.2]'''

Teoria dos números

prime_pi(1000000) # returns 78498, the number of primes less than one million
 
E = EllipticCurve('389a') # construct an elliptic curve from its Cremona label
P, Q = E.gens()
7 * P + Q # returns (24187731458439253/244328192262001 : 3778434777075334029261244/3819094217575529893001 : 1)

Ver também

• Mathematica
• William Stein

Ligações externas

• Sítio web do projecto SageMath
• Documentação oficial, referências e tutoriais do Sage
• Vídeos do Sage
• Utilize o Sage online em seu navegador
• AMS Notices Opinion – Open Source Mathematical Software
• W. Stein's blog post on history of Sage