Computação paralela
Computação paralela é uma forma de computação em que vários cálculos são realizados ao mesmo tempo,[1] operando sob o princípio de que grandes problemas geralmente podem ser divididos em problemas menores, que então são resolvidos concorrentemente (em paralelo). Existem diferentes formas de computação paralela: em bit, instrução, de dado ou de tarefa. A técnica de paralelismo já é empregada há vários anos, principalmente na computação de alto desempenho, mas recentemente o interesse no tema cresceu devido às limitações físicas que previnem o aumento de frequência de processamento.[2] Com o aumento da preocupação do consumo de energia dos computadores, a computação paralela se tornou o paradigma dominante nas arquiteturas de computadores sob forma de processadores multinúcleo.[3]
Computadores paralelos podem ser classificados de acordo com o nível em que o hardware suporta paralelismo. Computadores com multinúcleos ou multiprocessadores possuem múltiplos elementos de processamento em somente uma máquina, enquanto clusters, MPP e grades usam múltiplos computadores para trabalhar em uma única tarefa. Arquiteturas paralelas especializadas às vezes são usadas junto com processadores tradicionais, para acelerar tarefas específicas.
Programas de computador paralelos são mais difíceis de programar que sequenciais,[4] pois a concorrência introduz diversas novas classes de defeitos potenciais, como a condição de corrida. A comunicação e a sincronização entre diferentes subtarefas é tipicamente uma das maiores barreiras para atingir grande desempenho em programas paralelos. O aumento da velocidade por resultado de paralelismo é dado pela lei de Amdahl.
Visão geral[editar | editar código-fonte]
Tradicionalmente, o software tem sido escrito para ser executado sequencialmente. Para resolver um problema, um algoritmo é construído e implementado como um fluxo serial de instruções. Tais instruções são então executadas por uma unidade central de processamento de um computador. Somente uma instrução pode ser executada por vez; após sua execução, a próxima então é executada.[5]
Por outro lado, a computação paralela faz uso de múltiplos elementos de processamento simultaneamente para resolver um problema. Isso é possível ao quebrar um problema em partes independentes de forma que cada elemento de processamento pode executar sua parte do algoritmo simultaneamente com outros. Os elementos de processamento podem ser diversos e incluir recursos como um único computador com múltiplos processadores, diversos computadores em rede, hardware especializado ou qualquer combinação dos anteriores.[5]
O aumento da frequência de processamento foi o principal motivo para melhorar o desempenho dos computadores de meados da década de 1980 a 2004. Em termos gerais, o tempo de execução de um programa corresponde ao número de instruções multiplicado pelo tempo médio de execução por instrução. Mantendo todo o resto constante, aumentar a frequência de processamento de um computador reduz o tempo médio para executar uma instrução, reduzindo então o tempo de execução para todos os programas que exigem alta taxa de processamento (em oposição à operações em memória.)[6]
Entretanto, o consumo de energia de um chip é dado pela equação , em que é a potência desempenhada pelo processador, é a capacitância sendo trocada por ciclo de clock (proporcional ao número de transistores cujas entradas mudam), é a tensão e é a frequência do processador (ciclos por segundo). A energia total gasta é obtida por = em que é o tempo em que o processador ficou ligado. [7] Aumentar a frequência significa aumentar a quantidade de energia usada em um processador. Em 2004, esse aumento de consumo levou a Intel a cancelar seu modelos de processadores Tejas e Jayhawk, geralmente citado como o fim da frequência de processamento como paradigma predominante nas arquiteturas de computador.[8]
A lei de Moore é a observação empírica de que a densidade de transistores em um microprocessador dobra a cada 18 a 24 meses.[9] Apesar do consumo de energia e de repetidas previsões sobre seu fim, ela ainda vale. Com o fim do aumento da frequência de processamento, esses transistores adicionais podem ser usados para adicionar hardware à computação paralela.
Leis de Amdahl e Gustafson[editar | editar código-fonte]
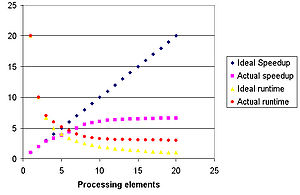
Teoricamente, o aumento de velocidade com o paralelismo deveria ser linear, de forma que dobrando a quantidade de elementos de processamento, reduz-se pela metade o tempo de execução. Entretanto, muitos poucos algoritmos paralelos atingem essa situação ideal. A maioria deles possui aumento de velocidade quase linear para poucos elementos de processamento, tendendo a um valor constante para uma grande quantidade de elementos.
O aumento de velocidade potencial de um algoritmo em uma plataforma de computação paralela é dado pela lei de Amdahl, formulada por Gene Amdahl na década de 1960.[11] Ela afirma que uma pequena porção do programa que não pode ser paralelizada limitará o aumento de velocidade geral disponível com o paralelismo. Qualquer grande problema da matemática ou da engenharia tipicamente consistirá de diversas partes paralelizáveis e diversas partes sequenciais. A relação entre os dois é dada pela equação:
em que é o aumento de velocidade do programa e é a fração paralelizável. Se a porção sequencial de um programa representa 10% do tempo de execução, não se pode obter mais que dez vezes de aumento de velocidade, independente de quantos processadores são adicionados. Isso limita a utilidade da adição de mais unidades paralelas de execução.
A lei de Gustafson está realacionada com a de Amdahl. Ela pode ser formulada como:
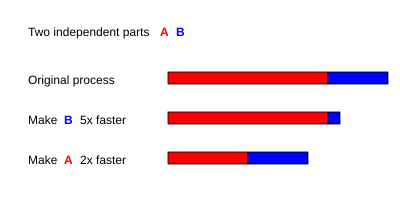
em que é o número de processadores, é o aumento de velocidade e é a parte não paralelizável do processo.[13] A lei de Amdahl assume um tamanho de problema fixo e que o tamanho da seção sequencial é independente do número de processadores, enquanto a lei de Gustafson não parte dessas premissas.
Dependências[editar | editar código-fonte]
Entender a dependência de dados é fundamental na implementação de algoritmos paralelos. Nenhum programa pode rodar mais rápido que a maior cadeia de cálculos dependentes (conhecido como caminho crítico), já que o cálculo depende do cálculo anterior da cadeia, sendo executado sequencialmente. Entretanto, a maioria dos algoritmos não consiste de somente uma longa cadeia de cálculos dependentes; geralmente há oportunidades para executar cálculos independentes em paralelo.
Assumindo os fragmentos de programa e . As condições de Bernstein[14] descrevem quando os dois fragmentos são independentes e podem ser executados em paralelo. Para , assume-se que são todas as variáveis de entrada e todas as variáveis de saída, e o mesmo para . e são independentes se:
A violação da primeira condição introduz uma dependência de fluxo, correspondendo ao primeiro fragmento produzindo um resultado usado pelo segundo. A segunda condição representa a antidependência, quando o primeiro fragmento sobrescreve uma variável necessária pela segunda expressão. A terceira condição é a dependência de saída. Quando duas variáveis escrevem no mesmo local, a saída final deve vir do segundo fragmento.[15]
Considerando as seguintes subrotinas, que demonstram diferentes tipos de dependências:
1: ROTINA dep(a, b) 2: c ← a · b 3: d ← 2 · c 4: FIM ROTINA
A operação 3 de Dep(a, b) não pode ser executada antes ou paralelamente à operação 2 porque a operação 3 usa o resultado da operação 2. Essa é uma violação da primeira condição, introduzindo a dependência de fluxo.
1: ROTINA no_dep(a, b) 2: c ← a · b 3: d ← 2 · b 4: e ← a + b 5: FIM ROTINA
Neste exemplo, não há dependências entre as instruções, então elas podem ser executadas em paralelo.
As condições de Bernstein não permitem que a memória seja compartilhada por diferentes processos. Para isso, é necessária alguma forma de assegurar a ordem de acesso ao recurso, como semáforos, barreiras ou alguma outra forma de sincronização.
Condições de corrida, exclusão mútua e lentidão paralela[editar | editar código-fonte]
Subtarefas de um programa paralelo são frequentemente chamadas threads. Algumas arquiteturas paralelas usam versões mais leves e menores de threads conhecidas como fibras, enquanto outras usam versões maiores chamadas processos. Entretanto, as threads são geralmente aceitas como o termo genérico para as subtarefas. Pelo menos uma variável do sistema geralmente é compartilhada por mais de uma thread. As instruções entre dois programas podem ser escalonadas em qualquer ordem. Por exemplo, considerando o seguinte programa:
| Thread A | Thread B |
|---|---|
| 1A: Ler a variável V | 1B: Ler a variável V |
| 2A: Adicionar 1 à variável V | 2B: Adicionar 1 à variável V |
| 3A: Escrever o resultado na variável V | 3B: Escrever o resultado na variável V |
Se a instrução 1B é executada entre 1A e 3A, ou se a instrução 1A é executada entre 1B e 3B, o programa produzirá dados incorretos, por conta de um problema conhecido como condição de corrida. O programador deve usar um bloqueio de acesso para prover exclusão mútua. Tal bloqueio é uma construção de uma linguagem de programação que permite a uma thread ter total controle de uma variável, prevenindo que outras threads acessem a mesma região de memória até que se faça o desbloqueio. A thread que detém o bloqueio é livre para executar sua região crítica. Para garantir a execução correta do programa, deve-se reescrevê-lo usando bloqueios:
| Thread A | Thread B |
|---|---|
| 1A: Bloquear a variável V | 1B: Bloquear a variável V |
| 2A: Ler a variável V | 2B: Ler a variável V |
| 3A: Adicionar 1 à variável V | 3B: Adicionar 1 à variável V |
| 4A: Escrever o resultado na variável V | 4B: Escrever o resultado na variável V |
| 5A: Desbloquear a variável V | 5B: Desbloquear a variável V |
Uma das duas threads conseguirá bloquear a variável, enquanto a outra ficará esperando impossibilitada de continuar sua execução até que o desbloqueio seja feito. Ainda que tal bloqueio garante a execução correta do programa, ele pode tornar o programa consideravelmente mais lento.
Bloquear múltiplas variáveis usando bloqueios não atômicos introduz a possibilidade de deadlock. Um bloqueio atômico bloqueia diversas variáveis simultaneamente. Não podendo bloquear qualquer uma delas, todo o bloqueio falha. Se duas threads precisam bloquear as mesmas duas variáveis usando bloqueios não atômicos, é possível que cada uma das threads bloqueie uma variável distinta. Nesse caso, nenhuma thread pode continuar e o deadlock ocorre.
Nem todo paralelismo resulta em aumento de velocidade. Geralmente, como uma tarefa é dividida em diversas threads, tais threads gastam determinado tempo comunicando-se com outras. Eventualmente, o overhead da comunicação domina o tempo gasto para resolver o problema. Nesse caso, quanto mais paralelismo é feito, mais lento é o tempo total de execução, um efeito conhecido como lentidão paralela.
Modelos de consistência[editar | editar código-fonte]

Linguagens de programação e computadores paralelos devem ter um modelo de consistência, também conhecido como modelo de memória, que define as regras de execução das operações em memória e como os resultados são produzidos.
Um dos primeiros modelos de consistência foi a consistência sequencial de Leslie Lamport. Tal modelo é a propriedade de que a execução de um programa paralelo produz o mesmo resultado que um programa sequencial. Especificamente, um programa é sequencialmente consistente se "… os resultados de qualquer de suas execuções é o mesmo se as operações de todos os processadores forem executadas em alguma ordem sequencial, e as operações de cada processador aparecem nessa sequência na ordem especificada pelo programa".[16]
Matematicamente, tais modelos podem ser representados de diversas formas. Introduzidas por Carl Adam Petri em sua tese de doutorado em 1962, as redes de Petri foram uma primeira abordagem para codificar as regras de modelos de consistência. Posteriormente a teoria de fluxos de dados foi construída, e arquiteturas de fluxo de dado foram criadas para implementar fisicamente as ideias da teoria de fluxo de dado. A partir do final da década de 1970, álgebras de processo como cálculo de sistemas de comunicação e processos de comunicação serial foram desenvolvidos para permitir a modelagem algébrica de sistemas compostos por componentes que interagem. Adições mais recentes à família, como o cálculo pi, adicionaram a capacidade de modelar topologias dinâmicas. Lógicas como o TLA+ e modelos matemáticos como traces também foram desenvolvidos par descrever o comportamento de sistemas concorrentes.
Taxonomia de Flynn[editar | editar código-fonte]
Michael J. Flynn criou um dos primeiros sistemas de classificação para computadores e programas paralelos e sequenciais, atualmente conhecida como taxonomia de Flynn. O cientista classificou os programas e computadores por quantidade de fluxos de instruções, e por quantidade de dados usadas por tais instruções.
A classificação SISD equivale a um programa inteiramente sequencial, e a classificação SIMD é análoga a fazer a mesma operação repetidamente por um grande conjunto de dados. A classificação MISD raramente é usada, já os programas MIMD são os programas paralelos mais comuns.
Tipos de paralelismo[editar | editar código-fonte]
No bit[editar | editar código-fonte]
A partir do advento da tecnologia de fabricação de chip VLSI na década de 1970 até cerca de 1986, o aumento da velocidade na arquitetura de computador era obtido dobrando-se o tamanho da palavra, a quantidade de informação que o processador pode executar por ciclo.[17] Aumentar o tamanho da palavra reduz a quantidade de instruções que um processador deve executar para realizar uma operação em variáveis cujo tamanho é maior do que o da palavra.
Historicamente, microprocessadores de quatro bits foram substituídos por oito, então para dezesseis e então para trinta e dois. A partir de então, o padrão 32-bit se manteve na computação de uso geral por duas décadas. Cerca de 2003, a arquitetura 64-bit começou a ganhar mais espaço.
Na instrução[editar | editar código-fonte]

Em sua essência, um programa de computador é um fluxo de instruções executadas por um processador. Tais instruções podem ser reordenadas e combinadas em grupos que então são executados em paralelo sem mudar o resultado do programa. Isso é conhecido por paralelismo em instrução. Avanços nessa técnica dominaram a arquitetura de computador de meados da década de 1980 até meados da década de 1990.[18]
Processadores modernos possuem pipeline com múltiplos estágios. Cada estágio corresponde a uma ação diferente que o processador executa em determinada instrução; um processador com um pipeline de N estágios pode ter até N diferentes instruções em diferentes estágios de execução. O exemplo canônico é o processador RISC, com cinco estágios: instruction fetch, decode, execute, memory access e write back. O processador Pentium 4 possui um pipeline de 35 estágios.[19]

Além do paralelismo em instrução obtido com o pipeline, alguns processadores podem lidar com mais de uma instrução por vez. São conhecidos como processadores superescalares. As instruções podem ser agrupadas somente se não há dependência de dados entre elas. O algoritmo de marcador e o algoritmo de Tomasulo são duas das técnicas mais usadas para implementar reordenação de execução e paralelismo em instrução.
No dado[editar | editar código-fonte]
O paralelismo em dado é inerente a laços de repetição, focando em distribuir o dado por diferentes nós computacionais para serem processados em paralelo. Diversas aplicações científicas e de engenharia apresentam esse tipo de paralelismo.
Uma dependência por laço é a dependência de uma iteração do laço com a saída de uma ou mais iterações anteriores, uma situação que impossibilita a paralelização de laços. Por exemplo, considerando o seguinte pseudocódigo que calcula os primeiros números de Fibonacci:
1: anterior2 ← 0 2: anterior1 ← 1 3: atual ← 1 4: FAÇA: 5: atual ← anterior1 + anterior2 6: anterior2 ← anterior1 7: anterior1 ← atual 8: ENQUANTO (atual < 10)
Esse laço não pode ser paralelizado porque atual depende de si (anterior1) e anterior2, que são calculados em cada iteração. Como cada iteração depende do resultado da anterior, elas não podem ser realizadas em paralelo. Com o aumento do tamanho de um problema, geralmente aumenta-se a quantidade de paralelismo em dado disponível.[20]
Na tarefa[editar | editar código-fonte]
Paralelismo em tarefa é a característica de um programa paralelo em que diferentes cálculos são realizados no mesmo ou em diferentes conjuntos de dados.[21] Isso contrasta com o paralelismo em dado, em que o mesmo cálculo é feito em diferentes conjuntos de dados. Paralelismo em tarefa geralmente não é escalável com o tamanho do problema.[20]
Hardware[editar | editar código-fonte]
Memória e comunicação[editar | editar código-fonte]
A memória principal de um computador paralelo é compartilhada (compartilhada entre os elementos de processamento num único espaço de endereçamento) ou distribuída (cada elemento de processamento possui seu próprio espaço de endereçamento).[22] Memória distribuída se refere ao fato da memória ser logicamente distribuído, mas frequentemente isso também implica na distribuíção física. A memória distribuída e compartilhada é uma combinação das duas abordagens, em que cada elemento de processamento possui sua memória local e acessa a memória de outros processadores remotos. Acesso à memória local é geralmente mais rápido que acesso à memória remota.
Arquiteturas de computador em que cada elemento da memória principal pode ser acessado com a mesma latência e banda são conhecidas como sistemas de Acesso à Memória Unificado. Isso geralmente é feito por um sistema com somente memória compartilhada. Um sistema que não possui tal propriedade é conhecido como sistema de Acesso à Memória Não-Unificado, o que inclui sistemas que utilizam memória distribuída.
Computadores fazem uso de cache, memórias pequenas e rápidas localizadas próximo ao processador, e que armazenam cópias temporárias de valores e memória. Computadores paralelos possuem dificuldades com caches que podem armazenar o mesmo valor em mais de um local, com a possibilidade de execução incorreta do programa. Tais sistemas existem um mecanismo de coerência de cache, que asseguram a execução correta. Desenvolver mecanismos de coerência de cache de alto desempenho é um problema muito difícil na arquitetura de computador. Como resultado, arquiteturas de memória compartilhada não escalonam tão bem quanto sistemas distribuídos.[22]
A comunicação dos processadores entre si e com as memórias podem ser implementadas em hardware de várias formas, incluindo por memória compartilhada, barramento compartilhado ou uma rede interconectada. Para o último caso, deve haver uma forma de roteamento para permitir a troca de mensagens entre nós que não estão diretamente conectados.
Software[editar | editar código-fonte]
Linguagens de programação paralelas[editar | editar código-fonte]
Linguagens de programação, bibliotecas, API e modelos foram criados para programar computadores paralelos. Geralmente divide-se em classes de plataformas, baseadas nas premissas sobre a arquitetura de memória usada, incluindo memória compartilhada, memória distribuída ou memória compartilhada e distribuída. Linguagens de programação de memória compartilhada se comunicam ao manipularem variáveis de memória compartilhada. Exemplos de uso do modelo incluem POSIX Threads e OpenMP. Já a memória distribuída faz uso de troca de mensagens. Exemplos de uso do modelo incluem Message Passing Interface. Um conceito usado em programação paralela é o valor futuro, quando uma parte do programa promete processar dados para outra parte de um programa em um momento futuro.
Paralelismo automático[editar | editar código-fonte]
A habilidade de um compilador realizar paralelismo automático de um programa sequencial é um dos assuntos mais estudados no campo de computação paralela. Entretanto, apesar de décadas de trabalho por pesquisadores de compiladores, pouco sucesso se teve na área.[23] Linguagens de programação paralelas de amplo uso continuam explícitas, isto é, requerendo a programação paralela propriamente dita; ou no máximo parcialmente implícitas, em que o programador fornece ao compilador diretivas para o paralelismo.
Aplicações[editar | editar código-fonte]
Com o desenvolvimento de computadores paralelos, torna-se mais viável resolver problemas anteriormente muito demorados para se executar. A computação paralela é usada em diversos campos, da bioinformática (para o enovelamento de proteínas) a economia (para simulações de matemática financeira). Tipos comuns de problemas encontrados em aplicações de computação paralela são:[24]
- Álgebra linear densa
- Álgebra linear esparsa
- Métodos espectrais
- Problemas N-body
- Problemas de grades estruturadas
- Problemas de grades não estruturadas
- Método de Monte Carlo
- Lógica combinacional
- Visita de grafo
- Programação dinâmica
- Métodos de ramificação e poda
- Modelos em grafo
- Simulação de máquina de estado finito
Referências
- ↑ Almasi, G.S. e A. Gottlieb (1989). Highly Parallel Computing. Benjamin-Cummings, Redwood City, CA.
- ↑ S.V. Adve et al. (Novembro de 2008). "Parallel Computing Research at Illinois: The UPCRC Agenda" Arquivado em 9 de dezembro de 2008, no Wayback Machine.. Parallel@Illinois, Universidade de Illinois.
- ↑ Asanovic, Krste et al. (18 de dezembro de 2006). "The Landscape of Parallel Computing Research: A View from Berkeley". Universidade da Califórnia, Berkeley. Technical Report UCB/EECS-2006-183.
- ↑ Patterson, David A. e John L. Hennessy (1998). Computer Organization and Design, Second Edition, Morgan Kaufmann Publishers, p. 715. ISBN 1558604286.
- ↑ a b Barney, Blaise. «Introduction to Parallel Computing». Lawrence Livermore National Laboratory. Consultado em 9 de novembro de 2007
- ↑ Hennessy, John L. e David A. Patterson (2002). Computer Architecture: A Quantitative Approach. 3ª edição, Morgan Kaufmann, p. 43. ISBN 1558607242.
- ↑ Rabaey, J. M. (1996). Digital Integrated Circuits. Prentice Hall, p. 235. ISBN 0131786091.
- ↑ Flynn, Laurie J. "Intel Halts Development of 2 New Microprocessors". The New York Times, 8 de maio de 2004.
- ↑ Gordon E. Moore (1965). «Cramming more components onto integrated circuits» (PDF). Electronics Magazine. Consultado em 4 de janeiro de 2009. Arquivado do original (PDF) em 18 de fevereiro de 2008
- ↑ Tradução do texto da imagemEixo da abcissa: elementos de processamentoLegenda azul: aumento de velocidade idealLegenda roxa: aumento de velocidade realLegenda amarela: tempo de execução idealLegenda vermelha: tempo de execução real
- ↑ Amdahl, G. (abril de 1967) "The validity of the single processor approach to achieving large-scale computing capabilities". Em Proceedings of AFIPS Spring Joint Computer Conference, Atlantic City, N.J., AFIPS Press, pp. 483–85.
- ↑ Tradução do texto da imagemDuas partes independentes A BPrimeira barra: processo originalTornar B 5x mais rápidaTornar A 2x mais rápida
- ↑ Reevaluating Amdahl's Law Arquivado em 27 de setembro de 2007, no Wayback Machine. (1988). Communications of the ACM 31(5), pp. 532–33.
- ↑ Bernstein, A. J. (Outubro de 1966). "Program Analysis for Parallel Processing', IEEE Trans. em Electronic Computers". EC-15, pp. 757–62.
- ↑ Roosta, Seyed H. (2000). "Parallel processing and parallel algorithms: theory and computation". Springer, p. 114. ISBN 0387987169.
- ↑ Lamport, Leslie (September 1979). "How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Programs", IEEE Transactions on Computers, C-28,9, pp. 690–91.
- ↑ Culler, David E.; Jaswinder Pal Singh e Anoop Gupta (1999). Parallel Computer Architecture - A Hardware/Software Approach. Morgan Kaufmann Publishers, p. 15. ISBN 1558603433.
- ↑ Culler et al. p. 15.
- ↑ Patt, Yale (Abril de 2004). "The Microprocessor Ten Years From Now: What Are The Challenges, How Do We Meet Them? Arquivado em 14 de abril de 2008, no Wayback Machine. (wmv). Palestra na Universidade Carnegie Mellon.
- ↑ a b Culler et al. p. 125.
- ↑ Culler et al. p. 124.
- ↑ a b Patterson and Hennessy, p. 713.
- ↑ Shen, John Paul e Mikko H. Lipasti (2005). Modern Processor Design: Fundamentals of Superscalar Processors. McGraw-Hill Professional. p. 561. ISBN 0070570647.
- ↑ Asanovic, Krste, et al. (18 de dezembro de 2006). The Landscape of Parallel Computing Research: A View from Berkeley. Universidade da Califórnia, Berkeley. Technical Report UCB/EECS-2006-183. Ver tabelas nas páginas 17-19.
Ligações externas[editar | editar código-fonte]
- Parallel Virtual Machine (PVM)
- Message Passing Interface (MPI)
- Open Cluster Framework
- Centros Nacionais de Processamento de Alto Desempenho (CENAPAD) - SP
- Centros Nacionais de Processamento de Alto Desempenho (CENAPAD) - CE
- «Introdução à Computação Paralela». - curso do IPRJ/UERJ com material online sobre Cuda, MPI, Threads, MapReduce, Hadoop e outros.



















