Número de Fibonacci

Yupana (em quíchua, "instrumento de contagem"): calculadora usada pelos incas, possivelmente baseada nos números de Fibonacci.

A sucessão de Fibonacci ou sequência de Fibonacci é uma sequência de números naturais, na qual os primeiros dois termos são 0 e 1, e cada termo subsequente corresponde à soma dos dois precedentes.

A sequência tem o nome do matemático pisano do século XIII Leonardo de Pisa, conhecido como Leonardo Fibonacci, e os termos da sequência são chamados números de Fibonacci. Os números de Fibonacci são, portanto, os números que compõem a seguinte sequência de números inteiros (sequência A000045 na OEIS):

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Em termos matemáticos, a sequência é definida recursivamente pela fórmula abaixo, sendo os dois primeiros termos F₀= 0 e F₁= 1.

$F(n) = \left\{ \begin{matrix} 0\,,\qquad\qquad\qquad\quad\,\ \ \,&&\mbox{se }n=0\,\ \ \\ 1,\qquad\qquad\qquad\qquad\,&&\mbox{se }n=1\ \ \,\\ F(n-1)+F(n-2)&&\mbox{se }n>1\ \ \end{matrix} \right.$

Em seu livro de 1202, intitulado Liber Abaci, Fibonacci introduziu a sequência na matemática da Europa Ocidental, embora ela já tivesse sido descrita anteriormente por matemáticos indianos. Pela convenção moderna, a sequência inicial com F₀ = 0. No Liber Abaci, ela começava com F₁ = 1, omitindo-se o zero inicial, e alguns ainda escrevem a sequência dessa forma.

A sequência de Fibonacci tem aplicações na análise de mercados financeiros, na ciência da computação e na teoria dos jogos. Também aparece em configurações biológicas, como, por exemplo, na disposição dos galhos das árvores ou das folhas em uma haste, no arranjo do cone da alcachofra, do abacaxi, ou no desenrolar da samambaia.

Origens

No ocidente, a sequência de Fibonacci apareceu pela primeira vez no livro Liber Abaci (1202) de Leonardo de Pisa, conhecido como Fibonacci, embora ela já tivesse sido descrita por matemáticos indianos. Fibonacci considerou o crescimento de uma população idealizada (não realista biologicamente) de coelhos. Os números descrevem o número de casais na população de coelhos depois de n meses se for suposto que:

• no primeiro mês nasce apenas um casal,
• casais amadurecem sexualmente (e reproduzem-se) apenas após o segundo mês de vida,
• não há problemas genéticos no cruzamento consanguíneo,
• todos os meses, cada casal fértil dá a luz a um novo casal, e
• os coelhos nunca morrem.

Mas genericamente, chama-se sequência de Fibonacci qualquer função g onde g(n + 2) = g(n) + g(n + 1). Essas funções são precisamente as de formato g(n) = aF(n) + bF(n + 1) para alguns números a e b, então as sequências de Fibonacci formam um espaço vetorial com as funções F(n) e F(n + 1) como base.

Em particular, a sequência de Fibonacci com F(1) = 1 e F(2) = 3 é conhecida como os números de Lucas. A importância dos números de Lucas L(n) reside no fato deles gerarem a Proporção áurea para as n-ésimas potências:

$\left( \frac 1 2 \left( 1 + \sqrt{5} \right) \right)^n = \frac 1 2 \left( L(n) + F(n) \sqrt{5} \right).$

Os números de Lucas se relacionam com os de Fibonacci pela fórmula:

$L(n) = F(n-1) + F(n+1).$

Com esta fórmula podemos montar a sequência de Fibonacci e descobrir, por exemplo, quantos coelhos foram gerados no sexto mês, basta aplicar a fórmula descrita acima até chegar ao ponto inicial de 1 e 1, como mostra a figura abaixo:

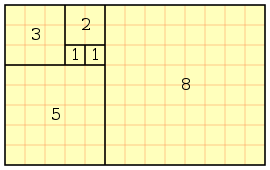
Ou seja, no sexto mês foram gerados 8 coelhos.

• F(6) = (F(6) - 1) + (F(6) - 2) = 5 e 4 → 8 ( Soma do Resultado de F(5) e F(4) )
• F(5) = (F(5) - 1) + (F(5) - 2) = 4 e 3 → 5 ( Soma do Resultado de F(4) e F(3) )
• F(4) = (F(4) - 1) + (F(4) - 2) = 3 e 2 → 3 ( Soma do Resultado de F(3) e F(2) )
• F(3) = (F(3) - 1) + (F(3) - 2) = 2 e 1 → 2
• F(2) = (F(2) - 1) + (F(2) - 2) = 1 e 0 → 1

e a primeira posição 1.

Note que a sequência de Fibonacci esta no resultado de cada posição: 1, 1, 2, 3, 5, 8, ...

Representações alternativas

Para analisar a sequência de Fibonacci (e, em geral, quaisquer sequências) é conveniente obter outras maneiras de representá-la matematicamente.

Função geradora

Uma função geradora para uma sequência qualquer $a_0,a_1,a_2,\dots$ é a função

$f(x) = a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+\cdots,$

ou seja, uma série potências formais em que cada coeficiente é um elemento da sequência. Os números de Fibonacci possuem a seguinte função geradora

$f\left(x\right)=\frac{x}{1-x-x^2}.$

Quando se expande esta função em potências de $x\,$, os coeficientes são justamente os termos da sequência de Fibonacci:

$\frac{x}{1-x-x^2}=0x^0+1x^1+1x^2+2x^3+3x^4+5x^5+8x^6+13x^7+\cdots$

Fórmula explícita

Conforme mencionado por Johannes Kepler, a taxa de crescimento dos números de Fibonacci, que é F(n + 1) /F(n), tende à Proporção áurea, denominada φ. Esta é a raiz positiva da equação de segundo grau x² − x − 1 = 0, então φ² = φ + 1. Se multiplicarmos ambos os lados por φⁿ, teremos φⁿ⁺² = φⁿ⁺¹ + φⁿ, então a função φⁿ é uma sequência de Fibonacci. É possível demonstrar que a raiz negativa da mesma equação, 1 − φ, tem as mesmas propriedades, então as duas funções φⁿ e (1 − φ)ⁿ formam outra base para o espaço.

Ajustando os coeficientes para obter os valores iniciais adequados F(0) = 0 e F(1) = 1, tem-se a fórmula de Binet:

$F\left(n\right) = \frac{1}{\sqrt{5}}\left\{ \left ( \frac{1+\sqrt{5}}{2} \right )^n - \left ( \frac{1-\sqrt{5}}{2} \right )^n \right \} = {\phi^n \over \sqrt{5}} - {(1-\phi)^n \over \sqrt{5}}.$

Este resultado também pode ser derivado utilizando-se a técnica de funções geradoras, ou a técnica de resolver relações de recorrência.

Quando n tende a infinito, o segundo termo tende a zero, e os números de Fibonacci tendem à exponencial φⁿ/√5. O segundo termo já começa pequeno o suficiente para que os números de Fibonacci possam ser obtidos usando somente o primeiro termo arredondado para o inteiro mais próximo.

Forma matricial

Para argumentos muito grandes, quando utiliza-se um computador bignum, é mais fácil^{[carece de fontes]} calcular os números de Fibonacci usando a seguinte equação matricial:

$\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^n = \begin{bmatrix} F\left(n+1\right) & F \left(n\right) \\ F\left(n\right) & F \left(n-1\right) \end{bmatrix},$

em que a potência de n é calculada elevando-se a matriz ao quadrado repetidas vezes.

Um exemplo de aplicação desta expressão matricial é na demonstração do teorema de Lamé sobre o algoritmo de Euclides para o cálculo do MDC. Veja por exemplo o capítulo sobre o máximo divisor comum do wikilivro de Teoria de números.

Representação da Série de Fibonacci na Molle Antonelliana em Turim, Itália.

Tipos de algoritmos

Há diversos algoritmos (métodos) para calcular o $n$-ésimo elemento da sequência de Fibonacci, sendo que os mais comuns empregam um das seguintes abordagens:

• Recursiva
• Iterativa
• Dividir para conquistar

A seguir é apresentado um exemplo de cada um destes tipos de algoritmos em pseudocódigo.

Abordagem recursiva

A própria definição da sequência de Fibonacci pode ser tomada como base para implementar um algoritmo recursivo que gera os termos da sequência, como é mostrado a seguir: função ${\it fib}(n)\,$

se $n<2\,$ então

retorne $n\,$

caso contrário

retorne ${\it fib}(n-1) + {\it fib}(n-2)\,$

Apesar de simples, essa estratégia não é recomendável porque os mesmos valores são calculados muitas vezes (a não ser que a linguagem de programação guarde automaticamente os valores calculados nas chamadas anteriores da mesma função com o mesmo argumento). Uma análise cuidadosa mostra que a complexidade computacional do algoritmo é $O(\varphi^n)\,$. Por esse motivo, normalmente calcula-se os números de Fibonacci "de baixo para cima",^{[carece de fontes]} começando com os dois valores 0 e 1, e depois repetidamente substituindo-se o primeiro número pelo segundo, e o segundo número pela soma dos dois anteriores.

Uma outra alternativa é fazer uso da fórmula apresentada na seção anterior, que envolve potências da proporção áurea. No entanto, isso pode não ser muito conveniente para valores grandes de n, já que os erros de arredondamento se acumulam e a precisão dos números de ponto flutuante normalmente não será suficiente.

Abordagem iterativa

Com o uso de um algoritmo iterativo como o que é mostrado a seguir, é possível obter a sequência um pouco mais eficientemente:

função ${\it fib}(n)\,$

$i\gets 1$

$j\gets 0$

para $k\,$ desde $1\,$ até $n\,$ faça

$t\gets i+j$

$i\gets j$

$j\gets t$

retorne $j\,$

Neste caso, a complexidade computacional do algoritmo é $O(n)\,$.

Abordagem dividir para conquistar

O algoritmo abaixo é bem mais eficiente e baseia-se na representação matricial da sequência de Fibonacci. Sua complexidade computacional é $O(\log(n))\,$.

função ${\it fib}(n)\,$

se $n\leq0$ então

retorne $0\,$

$i\gets n-1$

$(a,b) \gets (1,0)$

$(c,d) \gets (0,1)$

enquanto $i > 0\,$ faça

se $i\,$ é par então

$(a,b) \gets (db + ca, d(b + a) + cb)$

$(c,d) \gets (c^2 + d^2, d(2c + d))$

$i\gets i\div 2$

retorne $a+b\,$

Aplicações

Os números de Fibonacci são importantes para a análise em tempo real do algoritmo euclidiano, para determinar o máximo divisor comum de dois números inteiros.

Matiyasevich mostrou que os números de Fibonacci podem ser definidos por uma Equação diofantina, o que o levou à solução original do Décimo Problema de Hilbert.

Os números de Fibonacci aparecem na fórmula das diagonais de um triângulo de Pascal (veja coeficiente binomial).

Um uso interessante da sequência de Fibonacci é na conversão de milhas para quilômetros. Por exemplo, para saber aproximadamente a quantos quilômetros 5 milhas correspondem, pega-se o número de Fibonacci correspondendo ao número de milhas (5) e olha-se para o número seguinte (8). 5 milhas são aproximadamente 8 quilômetros. Esse método funciona porque, por coincidência, o fator de conversão entre milhas e quilômetros (1.609) é próximo de φ (1.618) (obviamente ele só é útil para aproximações bem grosseiras: além do factor de conversão ser diferente de φ, a série converge para φ).

Exemplo de sons Fibonacci

Em música os números de Fibonacci são utilizados para a afinação, tal como nas artes visuais, determinar proporções entre elementos formais. Um exemplo é a Música para Cordas, Percussão e Celesta de Béla Bartók.

Le Corbusier usou a sequência de Fibonacci na construção do seu modulor, um sistema de proporções baseadas no corpo humano e aplicadas ao projeto de arquitetura.

Em The Wave Principal, Elliot defende a ideia que as flutuações do mercado seguem um padrão de crescimento e decrescimento que pode ser analisado segundo os números de Fibonacci, uma vez determinada a escala de observação. Defende que as relações entre picos e vales do gráfico da flutuação de bolsa tendem a seguir razões numéricas aproximadas das razões de dois números consecutivos da sequência de Fibonacci.

Teorias mais recentes, defendem que é possível encontrar relações “de ouro” entre os pontos de pico e os de vale, como no gráfico abaixo:

Se tomarmos o valor entre o início do ciclo e o primeiro pico, e o compararmos com o valor entre este pico e o pico máximo, encontraremos também o número de ouro. O ciclo, naturalmente, pode estar invertido, e os momentos de pico podem se tornar momentos de vale, e vice-versa.

Generalizações

Uma generalização da sequência de Fibonacci são as sequências de Lucas. Um tipo pode ser definido por:

U(0) = 0

U(1) = 1

U(n+2) = PU(n+1) − QU(n)

onde a sequência normal de Fibonacci é o caso especial de P = 1 e Q = -1. Outro tipo de sequência de Lucas começa com V(0) = 2, V(1) = P. Tais sequências têm aplicações na Teoria de Números e na prova que um dado número é primo (primalidade).

Os polinômios de Fibonacci são outra generalização dos números de Fibonacci.

Identidades

• F(n + 1) = F(n) + F(n − 1)
• F(0) + F(1) + F(2) + … + F(n) = F(n + 2) − 1
• F(1) + 2 F(2) + 3 F(3) + … + n F(n) = n F(n + 2) − F(n + 3) + 2

É possível essas identidades usando diferentes métodos. Mas, entretanto, nós queremos demonstrar uma elegante prova para cada um de seus usos aqui. Particularmente, F(n) podem ser interpretados como o número de formas de adicionar 1's e 2's até n − 1, convencionando-se que F(0) = 0, significando que nenhuma soma irá adicionar até -1, e que F(1) = 1, significando que a soma 0 será "adicionada" até 0. Aqui a ordem dos números importa. Por exemplo, 1 + 2 e 2 + 1 são consideradas duas diferentes somas e são contadas duas vezes.

Prova da primeira identidade

Sem perda de generalidade, podemos assumir n ≥ 1. Então F(n + 1) conta o número de formas de somar 1's e 2's até n.

Quando a primeira parcela é 1, há F(n) formas de completar a contagem para n − 1; quando a primeira parcela é 2, há F(n − 1) formas de completar a contagem para n − 2. Portanto, no total, há F(n) + F(n − 1) formas de completar a contagem para n. $\Box$

Prova da segunda identidade

Contamos o número de formas de somar 1's e 2's até n + 1 de forma que pelo menos uma das parcelas é 2.

Como antes, há F(n + 2) formas de somar 1's e 2's até n + 1 quando n ≥ 0. Já que há apenas uma soma n + 1 que não usa nenhum 2, a saber 1 + … + 1 (n + 1 termos), subtraímos 1 de F(n + 2).

Equivalentemente, podemos considerar a primeira ocorrência de 2 como uma parcela.

Se, em uma soma, a primeira parcela é 2, então há F(n) formas de completar a contagem para n − 1. Se a segunda parcela é 2, mas a primeira é 1, então há F(n − 1) formas de completar a contagem para n − 2. Continuando este raciocínio iremos chegar à (n + 1)-ésima parcela. Se é 2, mas todas as n parcelas anteriores são 1's, então há F(0) formas de completar a contagem para 0. Se uma soma contém 2 como uma parcela, a primeira ocorrência de tal parcela deve tomar lugar entre a primeira e a (n + 1)-ésima posição. Portanto F(n) + F(n − 1) + … + F(0) dá a contagem desejada. $\Box$

Prova da Terceira Identidade

Essa identidade pode ser estabelecida em duas fases. Primeiro, contamos o número de formas de somar 1's e 2's até -1, 0, …, ou n + 1 tal que pelo menos uma das parcelas seja 2.

Pela nossa primeira igualdade, há F(n + 2) − 1 formas de somar até n + 1; F(n + 1) − 1 formas de somar até n; …; e, finalmente, F(2) − 1 formas de somar até 1.

Como F(1) − 1 = F(0) = 0 , podemos adicionar todos as somas n + 1 e aplicar a segunda igualdade novamente para obter:    [F(n + 2) − 1] + [F(n + 1) − 1] + … + [F(2) − 1]

= [F(n + 2) − 1] + [F(n + 1) − 1] + … + [F(2) − 1] + [F(1) − 1] + F(0)

= F(n + 2) + [F(n + 1) + … + F(1) + F(0)] − (n + 2)

= F(n + 2) + F(n + 3) − (n + 2).

Por outro lado , observamos a partir da segunda igualdadee que existem

• F(0) + F(1) + … + F(n − 1) + F(n) meios somando com n + 1;
• F(0) + F(1) + … + F(n − 1) meios somando com n;

……

• F(0) meio somando com -1.

Somando todas as somas n + 1 , vemos que há

• (n + 1) F(0) + n F(1) + … + F(n) formas de somar até -1, 0, …, ou n + 1.

Já que os dois métodos de contagem se referem ao mesmo número , temos : (n + 1) F(0) + n F(1) + … + F(n) = F(n + 2) + F(n + 3) − (n + 2)

Finalmente, completamos a prova subtraindo a igualdade acima de n + 1 vezes a segunda igualdade. $\Box$

Número Tribonacci

Um número Tribonacci assemelha-se a um número de Fibonacci, mas em vez de começarmos com dois termos pré-definidos, a sequência é iniciada com três termos pré-determinados, e cada termo posterior é a soma dos três termos precedentes. Os primeiros números de uma pequena sequência Tribonacci são: 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, 121415, 223317, etc.

A Sequência de Fibonacci na natureza

A sequência de Fibonacci está intrinsicamente ligada à natureza. Estes números são facilmente encontrados no arranjo de folhas do ramo de uma planta, em copas das árvores ou até mesmo no número de pétalas das flores.

As sementes das flores, frutos e, de forma particulamente interessante, as pinhas, trazem no seu escopo natural esta sequência. Como esta proporção trata-se de uma sucessão numérica, é possível perceber, em vários traços notáveis, a manifestação desta em muitos aspectos da natureza de maneira estética e funcional. Tal linha de análise é, muitas vezes, utilizada como base explicativa para a teoria criacionista denominada Design Inteligente.

Nautilus

A Sequencia Fibonacci no Nautilus.

Na espiral da concha do Nautilus, por exemplo, pode ser facilmente percebida a sequência de Fibonacci. A composição de quadrados com lados de medidas proporcionais aos números da sequência mostram a existência desta sucessão numérica nesta peça natural.

O primeiro quadrado terá os lados com medida 1, o segundo também, o terceiro terá os seus lados com medida 2, o quarto com medida 3, o quinto com medida 5, o sexto com medida 8 e, assim, sucessivamente.

Anatomia humana - dentição

Vistos frontalmente, os dentes anteriores estão na proporção áurea entre si. Por exemplo, a largura do incisivo central está proporcional à largura do incisivo lateral, assim como o incisivo lateral está proporcional ao canino, e o canino ao primeiro pré-molar.

O segmento “incisivo central até o primeiro pré-molar” se encontra na proporção áurea em relação ao canto da boca (final do sorriso). A altura do incisivo central está na proporção áurea em relação à largura dos dois centrais Na face relaxada, a linha dos lábios divide o terço inferior da face nos segmentos da proporção áurea: “da ponta do nariz à linha dos lábios” e “da linha dos lábios até o queixo”.(retângulo de ouro).

A espiral

Na espiral formada pela folha de uma bromélia, pode ser percebida a sequência de Fibonacci, através da composição de quadrados com arestas de medidas proporcionais aos elementos da sequência, por exemplo: 1, 1, 2, 3, 5, 8, 13… , tendentes à razão áurea. Este mesmo tipo de espiral também pode ser percebida na concha do Nautilus marinho.

Arranjos nas folhas

Os arranjos das folhas de algumas plantas em torno do caule são números de Fibonacci. Com este arranjo, todas as folhas conseguem apanhar os raios solares uniformemente. Esta formação, em caso de chuva, também facilita o escoamento da água na planta [1].

A Sequência de Fibonacci no cinema

O filme Pi de Darren Aronofsky apresenta várias referências à sequência de Fibonacci. Seu protagonista é Maximillian "Max" Cohen (Sean Gullette), um matemático brilhante e atormentado que tenta decodificar o padrão numérico do mercado de ações. Em uma cena, Max desenha quadrados com arestas de medidas proporcionais aos elementos da sequência de Fibonacci e os sobrepõe ao desenho do Homem Vitruviano de Leonardo da Vinci, trazendo-lhe certezas às suas convicções de que a matemática é a linguagem da natureza. Em outra cena, Max apanha uma concha em uma praia e observa a espiral nela descrita. Em outro trecho do filme, Max encontra o judeu Lenny Meyer, que lhe fala da crença em que a Torah seria uma sequência de números que formam um código enviado por Deus, quando entendidas as correspondências entre as letras do alfabeto hebraico a números. Max diz que alguns dos conceitos apresentados por Lenny são similares a uma sequência de Fibonacci.

Repfigits

Um repfigit ou número de Keith é um número inteiro, superior a 9, tal que os seus dígitos, ao começar uma sequência de Fibonacci, alcançam posteriormente o referido número. Um exemplo é 47, porque a sequência de Fibonacci que começa com 4 e 7 (4, 7, 11, 18, 29, 47) alcança o 47. Outro exemplo é 197: 1+9+7= 17, 9+7+17= 33, 7+17+33= 57, 17+33+57= 107, 33+57+107= 197.

Um repfigit pode ser uma sequência de Tribonacci se houver três dígitos no número, e de Tetranacci se o número tiver quatro dígitos, etc.

Alguns Números de Keith conhecidos: 14, 19, 28, 47, 61, 75, 197, 742, 1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909, 31331, 34285…

Ver também

• Proporção áurea
• Divisão em média e extrema razão
• György Dóczi

Ligações externas

• The Golden Section: Phi
• Computing Fibonacci numbers on a Turing Machine
• The Fibonacci Quarterly — um jornal acadêmico voltado ao estudo dos números de Fibonacci
• Algoritmo de Fibonacci em O(lg n)
• Implementações do algoritmo em diversas linguagens de programação no Rosetta Code