Saltar para o conteúdo

Padrões na natureza: diferenças entre revisões

Origem: Wikipédia, a enciclopédia livre.
Explorar interativamente o histórico
← Ver a alteração anteriorVer a alteração posterior →
Conteúdo apagado Conteúdo adicionado
VisualTexto wiki
Etiqueta: Inserção de predefinição obsoleta
Linha 22: Linha 22:
== História ==
== História ==


Os primeiros filósofos gregos tentaram explicar a ordem na [[natureza]], antecipando conceitos modernos. [[Pitágoras]] explicou os padrões da natureza, como as harmonias musicais, como decorrentes das propriedades [[número]], que ele considerava o constituinte básico da existência. [[Empédocles]] antecipou até certo ponto a explicação evolutiva de [[Charles Darwin|Darwin]] para as estruturas dos organismos. [[Platão]] defendeu a tese de universais naturais. Ele considerou que estes consistiam em formas ideais (εἶδος ''eidos'': "forma"), e os objetos físicos nada mais são que cópias imperfeitas. Assim, uma flor pode ser aproximadamente circular, mas nunca é um círculo perfeito.<ref>{{cite web |url=http://plato.stanford.edu/entries/platonism/ |website=[[Stanford Encyclopedia of Philosophy]] |title=Platonism in Metaphysics |orig-year=2004 |date=7 April 2009 |access-date=4 May 2012 |author=Balaguer, Mark}}</ref> [[Teofrasto]] observou que as plantas "que têm folhas planas as têm em uma série regular"; [[Plínio, o Velho]] notou seu arranjo circular padronizado.<ref name=livio110>{{cite book |last=Livio |first=Mario |author-link=Mario Livio |title=The Golden Ratio: The Story of Phi, the World's Most Astonishing Number |url=https://books.google.com/books?id=bUARfgWRH14C |orig-year=2002 |edition=First trade paperback |year=2003 |publisher=[[Random House|Broadway Books]] |location=New York |isbn=978-0-7679-0816-0 |page=110}}</ref> Séculos depois, [[Leonardo da Vinci]] notou o arranjo espiral dos padrões das folhas, que os troncos das árvores ganham anéis sucessivos à medida que envelhecem e propôs uma regra supostamente satisfeita para as áreas transversais dos galhos das árvores.<ref name=livio110/><ref>{{cite book |last=Da Vinci |first=Leonardo |editor-last=Taylor |editor-first=Pamela |title=The Notebooks of Leonardo da Vinci |publisher=New American Library |year=1971 |page=121}}</ref>
Os primeiros filósofos gregos tentaram explicar a ordem na [[natureza]], antecipando conceitos modernos. [[Pitágoras]] explicou os padrões da natureza, como as harmonias musicais, como decorrentes das propriedades [[número]], que ele considerava o constituinte básico da existência. [[Empédocles]] antecipou até certo ponto a explicação evolutiva de [[Charles Darwin|Darwin]] para as estruturas dos organismos. [[Platão]] defendeu a tese de universais naturais. Ele considerou que estes consistiam em formas ideais (εἶδος ''eidos'': "forma"), e os objetos físicos nada mais são que cópias imperfeitas. Assim, uma flor pode ser aproximadamente circular, mas nunca é um círculo perfeito.<ref>{{cite web |url=http://plato.stanford.edu/entries/platonism/ |website=[[Stanford Encyclopedia of Philosophy]] |title=Platonism in Metaphysics |orig-year=2004 |date=7 de abril de 2009 |access-date=4 de maio de 2012 |author=Balaguer, Mark}}</ref> [[Teofrasto]] observou que as plantas "que têm folhas planas as têm em uma série regular"; [[Plínio, o Velho]] notou seu arranjo circular padronizado.<ref name=livio110>{{cite book |last=Livio |first=Mario |author-link=Mario Livio |title=The Golden Ratio: The Story of Phi, the World's Most Astonishing Number |url=https://books.google.com/books?id=bUARfgWRH14C |orig-year=2002 |edition=First trade paperback |year=2003 |publisher=[[Random House|Broadway Books]] |location=New York |isbn=978-0-7679-0816-0 |page=110}}</ref> Séculos depois, [[Leonardo da Vinci]] notou o arranjo espiral dos padrões das folhas, que os troncos das árvores ganham anéis sucessivos à medida que envelhecem e propôs uma regra supostamente satisfeita para as áreas transversais dos galhos das árvores.<ref name=livio110/><ref>{{cite book |last=Da Vinci |first=Leonardo |editor-last=Taylor |editor-first=Pamela |title=The Notebooks of Leonardo da Vinci |publisher=New American Library |year=1971 |page=121}}</ref>


Em 1202, [[Leonardo Fibonacci]] introduziu a [[sequência de Fibonacci]] em seu livro ''[[Liber Abaci]]''.<ref>{{cite journal |last=Singh |first=Parmanand |title=Acharya Hemachandra and the (so called) Fibonacci Numbers |journal=Mathematics Education Siwan |year=1986 |volume=20 |issue=1 |pages=28–30 |issn=0047-6269 }}</ref> Fibonacci apresentou um [[experimento mental]] sobre o crescimento de uma população ideal de coelhos.<ref>{{cite web |last=Knott |first=Ron |title=Fibonacci's Rabbits |url=http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html#Rabbits |website=[[University of Surrey]] Faculty of Engineering and Physical Sciences}}</ref> [[Johannes Kepler]] apontou a presença da sequência de Fibonacci na natureza, usando-a para explicar a forma pentagonal de algumas flores.<ref name=livio110/> Em 1658, o médico e filósofo inglês [[Thomas Browne]] discutiu "como a natureza geometriza" em ''[[The Garden of Cyrus]]'', citando a numerologia pitagórica envolvendo o número 5 e a forma platônica do padrão [[quincunce]].<ref>{{cite book |author=Browne, Thomas |author-link=Sir Thomas Browne |url=http://penelope.uchicago.edu/gardennoframes/garden3.html |title=How Nature Geometrizeth |work=[[The Garden of Cyrus]] |date=1658}}</ref> Em 1754, [[Charles Bonnet]] observou que a [[filotaxia]] espiral das plantas era frequentemente expressa em séries de [[proporção áurea]] no sentido horário e anti-horário.<ref name=livio110/> Observações matemáticas da filotaxia seguiram-se com os trabalhos de [[Karl Friedrich Schimper]] e seu amigo [[Alexander Braun]]; [[Augusto Bravaise]] e seu irmão Louis conectou as taxas de filotaxia à sequência de Fibonacci em 1837, também observando sua aparência em pinhas e abacaxis.<ref name=livio110/> Em seu livro de 1854, o psicólogo alemão [[Adolf Zeising]] explorou a proporção áurea expressa no arranjo das partes das plantas, nos esqueletos dos animais e nos padrões de ramificação de suas veias e nervos, bem como nos [[cristal|cristais]].<ref>{{Cite book |title=Proportion: Science, Philosophy, Architecture |author=Padovan, Richard |author-link=Richard Padovan |publisher=Taylor & Francis |date=1999 |isbn=978-0-419-22780-9 |pages=305–306 |url=https://books.google.com/books?id=Vk_CQULdAssC&pg=PA306}}</ref><ref>{{cite journal |journal=Nexus Network Journal |first=Richard |last=Padovan |author-link=Richard Padovan |title=Proportion: Science, Philosophy, Architecture |volume=4 |pages=113–122 |doi=10.1007/s00004-001-0008-7 |date=2002 |issue=1 |doi-access=free}}</ref><ref>{{cite book |first=Adolf |last=Zeising |title=Neue Lehre van den Proportionen des meschlischen Körpers |date=1854 |page=preface |no-pp=true}}</ref>
Em 1202, [[Leonardo Fibonacci]] introduziu a [[sequência de Fibonacci]] em seu livro ''[[Liber Abaci]]''.<ref>{{cite journal |last=Singh |first=Parmanand |title=Acharya Hemachandra and the (so called) Fibonacci Numbers |journal=Mathematics Education Siwan |year=1986 |volume=20 |issue=1 |pages=28–30 |issn=0047-6269 }}</ref> Fibonacci apresentou um [[experimento mental]] sobre o crescimento de uma população ideal de coelhos.<ref>{{cite web |last=Knott |first=Ron |title=Fibonacci's Rabbits |url=http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html#Rabbits |website=[[University of Surrey]] Faculty of Engineering and Physical Sciences}}</ref> [[Johannes Kepler]] apontou a presença da sequência de Fibonacci na natureza, usando-a para explicar a forma pentagonal de algumas flores.<ref name=livio110/> Em 1658, o médico e filósofo inglês [[Thomas Browne]] discutiu "como a natureza geometriza" em ''[[The Garden of Cyrus]]'', citando a numerologia pitagórica envolvendo o número 5 e a forma platônica do padrão [[quincunce]].<ref>{{cite book |author=Browne, Thomas |author-link=Sir Thomas Browne |url=http://penelope.uchicago.edu/gardennoframes/garden3.html |title=How Nature Geometrizeth |work=[[The Garden of Cyrus]] |date=1658}}</ref> Em 1754, [[Charles Bonnet]] observou que a [[filotaxia]] espiral das plantas era frequentemente expressa em séries de [[proporção áurea]] no sentido horário e anti-horário.<ref name=livio110/> Observações matemáticas da filotaxia seguiram-se com os trabalhos de [[Karl Friedrich Schimper]] e seu amigo [[Alexander Braun]]; [[Augusto Bravaise]] e seu irmão Louis conectou as taxas de filotaxia à sequência de Fibonacci em 1837, também observando sua aparência em pinhas e abacaxis.<ref name=livio110/> Em seu livro de 1854, o psicólogo alemão [[Adolf Zeising]] explorou a proporção áurea expressa no arranjo das partes das plantas, nos esqueletos dos animais e nos padrões de ramificação de suas veias e nervos, bem como nos [[cristal|cristais]].<ref>{{Cite book |title=Proportion: Science, Philosophy, Architecture |author=Padovan, Richard |author-link=Richard Padovan |publisher=Taylor & Francis |date=1999 |isbn=978-0-419-22780-9 |pages=305–306 |url=https://books.google.com/books?id=Vk_CQULdAssC&pg=PA306}}</ref><ref>{{cite journal |journal=Nexus Network Journal |first=Richard |last=Padovan |author-link=Richard Padovan |title=Proportion: Science, Philosophy, Architecture |volume=4 |pages=113–122 |doi=10.1007/s00004-001-0008-7 |date=2002 |issue=1 |doi-access=free}}</ref><ref>{{cite book |first=Adolf |last=Zeising |title=Neue Lehre van den Proportionen des meschlischen Körpers |date=1854 |page=preface |no-pp=true}}</ref>
Linha 31: Linha 31:


<gallery mode=packed>
<gallery mode=packed>
File:Cycas circinalis male cone in Olomouc.jpg|O padrão de [[sequência de Fibonacci]] ocorre em plantas como a ''[[Cycas circinalis]]''.
File:Cycas circinalis male cone in Olomouc.jpg|O padrão da [[sequência de Fibonacci]] ocorre em plantas como a ''[[Cycas circinalis]]''.
File:National Aquatics Center Construction (cropped).jpg|O [[Centro Aquático Nacional de Pequim]] faz uso da [[Estructura de Weaire-Phelan|estrutura de Weaire–Phelan]].
File:National Aquatics Center Construction (cropped).jpg|O [[Centro Aquático Nacional de Pequim]] faz uso da [[Estructura de Weaire-Phelan|estrutura de Weaire–Phelan]].
File:Drcy.svg|D'Arcy Thompson foi pioneiro no estudo do crescimento e da forma em seu livro de 1917.
File:Drcy.svg|D'Arcy Thompson foi pioneiro no estudo do crescimento e da forma em seu livro de 1917.
</gallery>

== Causas ==
[[Ficheiro:Aphids and live young under Sycamore leaf.JPG|180px|miniaturadaimagem|direita|Padrões compostos: [[afídio|pulgões]] e filhotes recém-nascidos em aglomerados em forma de matriz na folha de [[Ficus sycomorus|sicômoro]], divididos em [[polígono]]s por veias, que são evitados pelos pulgões jovens.]]
Seres vivos como [[orquídea]]s, [[beija-flor]]es e a [[coloração estrutural|cauda do pavão]] têm desenhos abstratos com forma, padrão e cor que são considerados por muitos como belo, como algo a ser alcançado pela arte.<ref name=ForbesGuardian>Forbes, Peter. ''All that useless beauty''. The Guardian. Review: Non-fiction. 11 de fevereiro de 2012.</ref> A beleza que as pessoas percebem na natureza tem causas em diferentes níveis, notadamente na matemática que governa quais padrões podem se formar fisicamente, e entre os seres vivos nos efeitos da seleção natural, que governam como os padrões evoluem.{{sfn|Stevens|1974|page=222}}

A matemática procura descobrir e explicar padrões abstratos ou regularidades de todos os tipos.<ref name=Steen>{{cite journal |last1=Steen |first1=L.A. |author-link=Lynn Steen |year=1988 |title=The Science of Patterns |url= http://www.ascd.org/publications/curriculum-handbook/409/chapters/The-Future-of-Mathematics-Education.aspx |journal=[[Science (journal)|Science]] |volume=240 |issue=4852 |pages=611–616 |doi=10.1126/science.240.4852.611 |pmid=17840903 |bibcode=1988Sci...240..611S |s2cid=4849363 }}</ref><ref name=Devlin>[[Keith Devlin|Devlin, Keith]]. ''Mathematics: The Science of Patterns: The Search for Order in Life, Mind and the Universe'' (Scientific American Paperback Library) 1996</ref> Padrões visuais na natureza encontram explicações na [[teoria do caos]], [[fractal|fractais]], [[logaritmo|espirais logarítmicas]], [[topologia (matemática)|topologia]] e outros padrões matemáticos. Por exemplo, os [[L-Sistema|sistemas-L]] formam modelos convincentes de diferentes padrões de crescimento de árvores.<ref name=L/>

As leis da física aplicam as abstrações da matemática ao mundo real, muitas vezes como se fosse perfeito. Por exemplo, um cristal é perfeito quando não apresenta defeitos estruturais, como discordâncias, e é totalmente simétrico. A perfeição matemática exata só pode aproximar objetos reais.<ref name=Tatarkiewicz>{{cite journal |last=Tatarkiewicz |first=Władysław |author-link=Władysław Tatarkiewicz |title=Perfection in the Sciences. II. Perfection in Physics and Chemistry |journal=Dialectics and Humanism |volume=7 |issue=2 (spring 1980) |page=139}}</ref> Padrões visíveis na natureza são governados por leis físicas; por exemplo, os meandros podem ser explicados usando a [[dinâmica de fluidos]].

Em biologia, a [[seleção natural]] pode causar o desenvolvimento de padrões nos seres vivos por várias razões, incluindo [[camuflagem]],<ref name=DarwinCh4/> [[seleção sexual]],<ref name=DarwinCh4>[[Charles Darwin|Darwin, Charles]]. ''On the Origin of Species''. 1859, chapter 4.</ref> e diferentes tipos de sinalização, incluindo [[mimetismo]]<ref name=Wickler>{{cite book |last=Wickler |first=Wolfgang |author-link=Wolfgang Wickler |date=1968 |title=Mimicry in plants and animals |publisher=McGraw-Hill |location=New York |url=https://archive.org/details/mimicryinplantsa00wick |url-access=registration}}</ref> e [[simbiose de limpeza]].<ref name=PoulinGrutter>{{cite journal |last1=Poulin |first1=R. |last2=Grutter |first2=A.S. |date=1996 |jstor=1312929 |title=Cleaning symbioses: proximate and adaptive explanations |journal=BioScience |volume=46 |issue=7 |pages=512–517 |doi=10.2307/1312929|doi-access=free }}</ref> Nas plantas, as formas, cores e padrões de [[síndrome de polinização|flores polinizadas por insetos]], como o [[lírio]], evoluíram para atrair insetos como as [[abelha]]s. Padrões radiais de cores e listras, alguns visíveis apenas na luz ultravioleta, servem como guias de néctar que pode ser visto à distância.<ref>{{cite web |last=Koning |first=Ross |url=http://plantphys.info/plants_human/pollenadapt.shtml |title=Plant Physiology Information Website |website=Pollination Adaptations |date=1994 |access-date=2 de maio de 2012 }}</ref>

== Formação de padrões ==
{{AP|Formação de padrões}}
[[Alan Turing]],<ref name=Turing/> e mais tarde o biólogo matemático [[James Murray]],<ref name="Murray2013">{{cite book |last=Murray |first=James D. |title=Mathematical Biology |url=https://books.google.com/books?id=K3LmCAAAQBAJ&pg=PA436 |date=9 March 2013 |publisher=Springer Science & Business Media |isbn=978-3-662-08539-4 |pages=436–450}}</ref> descreveram um mecanismo que cria espontaneamente padrões manchados ou listrados: um [[Modelo de reação-difusão|sistema de reação-difusão]].{{sfn|Ball|2009a|pages=159–167}} As células de um organismo jovem têm genes que podem ser ativados por um sinal químico, um [[morfogênio]], resultando no crescimento de um certo tipo de estrutura, por exemplo uma mancha de pele escura. Se o morfogênio estiver presente em todos os lugares, o resultado é uma pigmentação uniforme, como em um leopardo preto. Mas se for distribuído de forma desigual, podem ocorrer manchas ou listras. Turing sugeriu que poderia haver ''[[retroalimentação|feedback]]'' no controle da produção do próprio morfogênio. Isso pode causar flutuações contínuas na quantidade de morfogênio à medida que se difunde pelo corpo. Um segundo mecanismo é necessário para criar padrões de [[onda estacionária|ondas estacionárias]] (para resultar em manchas ou listras): um inibidor químico que desliga a produção do morfogênio e que se difunde pelo corpo mais rapidamente do que o morfogênio, resultando em um esquema ativador-inibidor. A [[reação de Belousov-Zhabotinsky]] é um exemplo não biológico desse tipo de esquema, um oscilador químico.{{sfn|Ball|2009a|pages=159–167}}

Pesquisas posteriores conseguiram criar modelos convincentes de padrões tão diversos quanto listras de zebra, manchas de girafa, manchas de onça e padrões de casca de joaninha.{{sfn|Ball|2009a|pages=168–180}} Os modelos de ativação-inibição de [[Richard Prum]], desenvolvidos a partir do trabalho de Turing, usam seis variáveis ​​para explicar o intervalo observado de nove padrões básicos de pigmentação dentro da pena, desde o mais simples, uma mancha de pigmento central, através de manchas concêntricas, barras, divisas, ponto ocular, par de pontos centrais, fileiras de pontos emparelhados e uma matriz de pontos.{{sfn|Rothenberg|2011|pages=93–95}}<ref name=Prum/> Modelos mais elaborados simulam padrões complexos de penas na galinha-d'angola ''[[Numida meleagrisem]]'' que as penas individuais apresentam transições de barras na base para uma matriz de pontos na extremidade (distal). Estes requerem uma oscilação criada por dois sinais inibidores, com interações no espaço e no tempo.<ref name=Prum>{{cite journal |url=http://www.yale.edu/eeb/prum/pdf/Prum%20&%20Williamson%202002.pdf |title=Reaction–diffusion models of within-feather pigmentation patterning |last1=Prum |first1=Richard O. |author1-link=Richard Prum |last2=Williamson |first2=Scott |journal=Proceedings of the Royal Society of London B |date=2002 |volume=269 |issue=1493 |pages=781–792 |doi=10.1098/rspb.2001.1896|pmid=11958709 |pmc=1690965}}</ref>

Padrões podem se formar por outras razões na [[vegetação padronizada|paisagem vegetada]] de mata-tigre<ref name=TigerBush>{{cite book |title=Banded vegetation patterning in arid and semiarid environments |publisher=Springer-Verlag |last1=Tongway |first1=D. J. |author2=Valentin, C. |author3=Seghieri, J. |date=2001 |location=New York}}</ref> e ondas de abetos.<ref name=FirWave>{{cite web |url=http://tiee.esa.org/vol/v1/figure_sets/disturb/disturb_back4.html |title=Fir Waves: Regeneration in New England Conifer Forests |website=TIEE |date=22 February 2004 |access-date=26 May 2012 |author=D'Avanzo, C.}}</ref> Listras de arbustos de tigre ocorrem em encostas áridas, onde o crescimento das plantas é limitado pela chuva. Cada faixa de vegetação mais ou menos horizontal coleta efetivamente a água da chuva da zona nua imediatamente acima dela.<ref name=TigerBush/> Ondas de abeto ocorrem em florestas nas encostas das montanhas após a perturbação do vento, durante a regeneração. Quando as árvores caem, as árvores que elas abrigavam ficam expostas e, por sua vez, são mais propensas a serem danificadas, de modo que as lacunas tendem a se expandir na direção do vento. Enquanto isso, a barlavento, crescem árvores jovens, protegidas pela sombra do vento das árvores altas remanescentes.<ref name=FirWave/> Os padrões naturais às vezes são formados por animais, como nos montes Mima do noroeste dos Estados Unidos e algumas outras áreas, que parecem ser criados ao longo de muitos anos pelas atividades escavadoras de [[Geomyidae|esquilos de bolso]],<ref name=BBC>{{cite web |last=Morelle |first=Rebecca |author-link=Rebecca Morelle |title='Digital gophers' solve Mima mound mystery |url=https://www.bbc.co.uk/news/science-environment-25259133 |website=BBC News |access-date=9 December 2013|date=2013-12-09 }}</ref> enquanto os chamados [[Anel de fadas|círculos de fadas]] da Namíbia parece ser criada pela interação de grupos concorrentes de cupins de areia, juntamente com a competição por água entre as plantas do deserto.<ref>{{cite news |last1=Sample |first1=Ian |title=The secret of Namibia's 'fairy circles' may be explained at last |url=https://www.theguardian.com/science/2017/jan/18/the-secret-of-namibias-fairy-circles-may-be-explained-at-last |newspaper=[[The Guardian]] |access-date=18 January 2017 |date=18 January 2017}}</ref>

Em solos de permafrost com uma camada superior ativa sujeita a congelamento e degelo anual, o [[solo poligonal|solo padronizado]] pode se formar, criando círculos, redes, polígonos de [[cunha de gelo]], degraus e listras. A [[contração térmica]] causa a formação de trincas de retração; no degelo, a água preenche as rachaduras, expandindo-se para formar gelo na próxima vez que congelar e alargando as rachaduras em fatias. Essas rachaduras podem se unir para formar polígonos e outras formas.<ref>{{cite web |title=Permafrost: Patterned Ground |url=http://permafrosttunnel.crrel.usace.army.mil/permafrost/patterned_ground.html |website=US Army Corps of Engineers |access-date=17 de fevereiro de 2015 |archive-url=https://web.archive.org/web/20150307013043/http://permafrosttunnel.crrel.usace.army.mil/permafrost/patterned_ground.html |archive-date=7 de março de 2015 }}</ref>

O padrão fissurado que se desenvolve nos cérebros dos vertebrados é causado por um processo físico de expansão restrita dependente de dois parâmetros geométricos: expansão cortical tangencial relativa e espessura relativa do [[córtex cerebral|córtex]]. Padrões semelhantes de [[giro]]s (picos) e [[sulco]]s (depressões) foram demonstrados em modelos do cérebro a partir de géis lisos em camadas, com os padrões causados ​​por forças mecânicas compressivas resultantes da expansão da camada externa (representando o córtex) após o adição de um solvente. Modelos numéricos em simulações de computador suportam observações naturais e experimentais de que os padrões de dobramento da superfície aumentam em cérebros maiores.<ref name="Scientific American">{{cite web |url=https://www.scientificamerican.com/article/human-brain-s-bizarre-folding-pattern-re-created-in-a-vat/ |last1=Ghose |first1=Tia |title=Human Brain's Bizarre Folding Pattern Re-Created in a Vat |website=[[Scientific American]] |access-date=5 de abril de 2018}}</ref><ref name="PNAS">{{cite journal |last1=Tallinen |first1=Tuoma|last2=Chung |first2=Jun Young |last3=Biggins |first3= John S. |last4=Mahadevan |first4=L. |title=Gyrification from constrained cortical expansion |journal=Proceedings of the National Academy of Sciences of the United States of America |volume=111 |issue=35 |pages=12667–12672 |date=2014 |doi=10.1073/pnas.1406015111 |pmid=25136099 |arxiv=1503.03853 |pmc=4156754 |bibcode=2014PNAS..11112667T|doi-access=free}}</ref>

<gallery mode=packed class="center">
File:Giant Puffer fish skin pattern.JPG|[[Baiacu-gigante]], ''Tetraodon mbu''
File:Giant Pufferfish skin pattern detail.jpg|Detalhe do padrão de pele do baiacu-gigante
File:Belousov-Zhabotinsky Reaction Simulation Snapshot.jpg|Simulação computacional da [[reação de Belousov-Zhabotinsky]]
File:Tiger Bush Niger Corona 1965-12-31.jpg|Vista aérea de um planalto de mata-tigre no Níger
File:Fir waves.jpg|Ondas de abeto em White Mountains, New Hampshire
File:Melting pingo wedge ice.jpg|Solo padronizado: um [[pingo]] derretendo com polígonos de cunha de gelo ao redor perto de Tuktoyaktuk, Canadá
File:Fairy circles namibia.jpg|Círculos de fadas na área na Namíbia
File:02 1 facies dorsalis cerebri.jpg|Cérebro humano (visão superior) exibindo padrões de giros e sulcos
</gallery>
</gallery>


Revisão das 02h08min de 17 de abril de 2023

Padrões naturais se formam quando o vento sopra a areia nas dunas do deserto do Namibe. As dunas em forma de crescente e as ondulações em suas superfícies se repetem onde quer que haja condições adequadas.
Padrões do camaleão velado, Chamaeleo calyptratus, fornecem camuflagem e sinal de humor, bem como condição de reprodução.

Padrões na natureza são regularidades visíveis de forma encontradas no mundo natural. Esses padrões se repetem em diferentes contextos e às vezes podem ser modelizados matematicamente. Padrões naturais incluem simetrias, árvores, espirais, meandros, ondas, espumas, mosaicos, rachaduras e listras.[1] Os primeiros filósofos gregos já haviam estudado essa questão, com Platão, Pitágoras e Empédocles tentando explicar a ordem na natureza. A compreensão moderna dos padrões visíveis desenvolveu-se gradualmente ao longo do tempo.

No século XIX, o físico belga Joseph Plateau examinou películas de sabão, levando-o a formular o conceito de superfície mínima. O biólogo e artista alemão Ernst Haeckel pintou centenas de organismos marinhos para enfatizar sua simetria. O biólogo escocês D'Arcy Thompson foi pioneiro no estudo dos padrões de crescimento em plantas e animais, mostrando que equações simples poderiam explicar o crescimento em espiral. No século XX, o matemático britânico Alan Turing previu mecanismos de morfogênese que dão origem a padrões de manchas e listras. O biólogo húngaro Aristid Lindenmayer e o matemático franco-estadunidense Benoît Mandelbrot mostraram como a matemática dos fractais poderia descrever padrões de crescimento de plantas.

A matemática, a física e a química procuram explicar padrões na natureza em diferentes níveis e escalas. Os padrões em seres vivos são explicados pelos processos biológicos de seleção natural e seleção sexual. Estudos de formação de padrões fazem uso de modelos computacionais para simular uma ampla gama de padrões.

História

Os primeiros filósofos gregos tentaram explicar a ordem na natureza, antecipando conceitos modernos. Pitágoras explicou os padrões da natureza, como as harmonias musicais, como decorrentes das propriedades número, que ele considerava o constituinte básico da existência. Empédocles antecipou até certo ponto a explicação evolutiva de Darwin para as estruturas dos organismos. Platão defendeu a tese de universais naturais. Ele considerou que estes consistiam em formas ideais (εἶδος eidos: "forma"), e os objetos físicos nada mais são que cópias imperfeitas. Assim, uma flor pode ser aproximadamente circular, mas nunca é um círculo perfeito.[2] Teofrasto observou que as plantas "que têm folhas planas as têm em uma série regular"; Plínio, o Velho notou seu arranjo circular padronizado.[3] Séculos depois, Leonardo da Vinci notou o arranjo espiral dos padrões das folhas, que os troncos das árvores ganham anéis sucessivos à medida que envelhecem e propôs uma regra supostamente satisfeita para as áreas transversais dos galhos das árvores.[3][4]

Em 1202, Leonardo Fibonacci introduziu a sequência de Fibonacci em seu livro Liber Abaci.[5] Fibonacci apresentou um experimento mental sobre o crescimento de uma população ideal de coelhos.[6] Johannes Kepler apontou a presença da sequência de Fibonacci na natureza, usando-a para explicar a forma pentagonal de algumas flores.[3] Em 1658, o médico e filósofo inglês Thomas Browne discutiu "como a natureza geometriza" em The Garden of Cyrus, citando a numerologia pitagórica envolvendo o número 5 e a forma platônica do padrão quincunce.[7] Em 1754, Charles Bonnet observou que a filotaxia espiral das plantas era frequentemente expressa em séries de proporção áurea no sentido horário e anti-horário.[3] Observações matemáticas da filotaxia seguiram-se com os trabalhos de Karl Friedrich Schimper e seu amigo Alexander Braun; Augusto Bravaise e seu irmão Louis conectou as taxas de filotaxia à sequência de Fibonacci em 1837, também observando sua aparência em pinhas e abacaxis.[3] Em seu livro de 1854, o psicólogo alemão Adolf Zeising explorou a proporção áurea expressa no arranjo das partes das plantas, nos esqueletos dos animais e nos padrões de ramificação de suas veias e nervos, bem como nos cristais.[8][9][10]

No século XIX, o físico belga Joseph Plateau formulou o problema matemático da existência de uma superfície mínima com um determinado limite. Ele estudou intensamente as películas de sabão, formulando as leis de Plateau, que descrevem as estruturas formadas por filmes em espumas.[11] William Thomson identificou o problema da maneira mais eficiente de embalar células de igual volume como uma espuma em 1887; sua solução usa apenas um sólido, o favo de mel cúbico bitruncado com faces ligeiramente curvas para atender às leis de Plateau. Nenhuma solução melhor foi encontrada até 1993, quando Denis Weaire e Robert Phelan propuseram a estrutura de Weaire-Phelan; o Centro Aquático Nacional de Pequim adaptou a estrutura para sua parede externa nos Jogos Olímpicos de Verão de 2008.[12] O fotógrafo americano Wilson Bentley tirou a primeira micrografia de um floco de neve em 1885.[13]

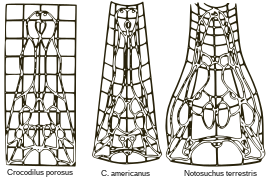
No século XX, A. H. Church estudou os padrões de filotaxia em seu livro de 1904.[14] Em 1917, D'Arcy Wentworth Thompson publicou On Growth and Form; sua descrição da filotaxia e da sequência de Fibonacci, as relações matemáticas nos padrões de crescimento espiral das plantas mostraram que equações simples poderiam descrever os padrões de crescimento espiral de chifres de animais e conchas de moluscos.[15] Em 1952, o cientista da computação Alan Turing escreveu "The Chemical Basis of Morphogenesis", uma análise dos mecanismos que seriam necessários para criar padrões em organismos vivos, no processo chamado morfogênese.[16] Ele previu reações químicas oscilantes, em particular a reação de Belousov-Zhabotinsky. Esses mecanismos de ativação-inibição podem, sugeriu Turing, gerar padrões (chamados padrões de Turing) de listras e manchas em animais e contribuir para os padrões espirais vistos na filotaxia vegetal.[17] Em 1968, o biólogo teórico húngaro Aristid Lindenmayer desenvolveu o sistema-L, uma gramática formal que pode ser usada para modelizar padrões de crescimento de plantas no estilo de fractais.[18] Os sistemas-L têm um alfabeto de símbolos que podem ser combinados usando regras de produção para construir sequências maiores de símbolos e um mecanismo para traduzir as sequências geradas em estruturas geométricas. Em 1975, após séculos de lento desenvolvimento da matemática dos padrões por Gottfried Leibniz, Georg Cantor, Helge von Koch, Wacław Sierpiński e outros, Benoît Mandelbrot escreveu um artigo de larga repercussão, "How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension", cristalizando o pensamento matemático no conceito de fractal.[19]

Causas

Padrões compostos: pulgões e filhotes recém-nascidos em aglomerados em forma de matriz na folha de sicômoro, divididos em polígonos por veias, que são evitados pelos pulgões jovens.

Seres vivos como orquídeas, beija-flores e a cauda do pavão têm desenhos abstratos com forma, padrão e cor que são considerados por muitos como belo, como algo a ser alcançado pela arte.[20] A beleza que as pessoas percebem na natureza tem causas em diferentes níveis, notadamente na matemática que governa quais padrões podem se formar fisicamente, e entre os seres vivos nos efeitos da seleção natural, que governam como os padrões evoluem.[21]

A matemática procura descobrir e explicar padrões abstratos ou regularidades de todos os tipos.[22][23] Padrões visuais na natureza encontram explicações na teoria do caos, fractais, espirais logarítmicas, topologia e outros padrões matemáticos. Por exemplo, os sistemas-L formam modelos convincentes de diferentes padrões de crescimento de árvores.[18]

As leis da física aplicam as abstrações da matemática ao mundo real, muitas vezes como se fosse perfeito. Por exemplo, um cristal é perfeito quando não apresenta defeitos estruturais, como discordâncias, e é totalmente simétrico. A perfeição matemática exata só pode aproximar objetos reais.[24] Padrões visíveis na natureza são governados por leis físicas; por exemplo, os meandros podem ser explicados usando a dinâmica de fluidos.

Em biologia, a seleção natural pode causar o desenvolvimento de padrões nos seres vivos por várias razões, incluindo camuflagem,[25] seleção sexual,[25] e diferentes tipos de sinalização, incluindo mimetismo[26] e simbiose de limpeza.[27] Nas plantas, as formas, cores e padrões de flores polinizadas por insetos, como o lírio, evoluíram para atrair insetos como as abelhas. Padrões radiais de cores e listras, alguns visíveis apenas na luz ultravioleta, servem como guias de néctar que pode ser visto à distância.[28]

Formação de padrões

Ver artigo principal: Formação de padrões

Alan Turing,[16] e mais tarde o biólogo matemático James Murray,[29] descreveram um mecanismo que cria espontaneamente padrões manchados ou listrados: um sistema de reação-difusão.[30] As células de um organismo jovem têm genes que podem ser ativados por um sinal químico, um morfogênio, resultando no crescimento de um certo tipo de estrutura, por exemplo uma mancha de pele escura. Se o morfogênio estiver presente em todos os lugares, o resultado é uma pigmentação uniforme, como em um leopardo preto. Mas se for distribuído de forma desigual, podem ocorrer manchas ou listras. Turing sugeriu que poderia haver feedback no controle da produção do próprio morfogênio. Isso pode causar flutuações contínuas na quantidade de morfogênio à medida que se difunde pelo corpo. Um segundo mecanismo é necessário para criar padrões de ondas estacionárias (para resultar em manchas ou listras): um inibidor químico que desliga a produção do morfogênio e que se difunde pelo corpo mais rapidamente do que o morfogênio, resultando em um esquema ativador-inibidor. A reação de Belousov-Zhabotinsky é um exemplo não biológico desse tipo de esquema, um oscilador químico.[30]

Pesquisas posteriores conseguiram criar modelos convincentes de padrões tão diversos quanto listras de zebra, manchas de girafa, manchas de onça e padrões de casca de joaninha.[31] Os modelos de ativação-inibição de Richard Prum, desenvolvidos a partir do trabalho de Turing, usam seis variáveis ​​para explicar o intervalo observado de nove padrões básicos de pigmentação dentro da pena, desde o mais simples, uma mancha de pigmento central, através de manchas concêntricas, barras, divisas, ponto ocular, par de pontos centrais, fileiras de pontos emparelhados e uma matriz de pontos.[32][33] Modelos mais elaborados simulam padrões complexos de penas na galinha-d'angola Numida meleagrisem que as penas individuais apresentam transições de barras na base para uma matriz de pontos na extremidade (distal). Estes requerem uma oscilação criada por dois sinais inibidores, com interações no espaço e no tempo.[33]

Padrões podem se formar por outras razões na paisagem vegetada de mata-tigre[34] e ondas de abetos.[35] Listras de arbustos de tigre ocorrem em encostas áridas, onde o crescimento das plantas é limitado pela chuva. Cada faixa de vegetação mais ou menos horizontal coleta efetivamente a água da chuva da zona nua imediatamente acima dela.[34] Ondas de abeto ocorrem em florestas nas encostas das montanhas após a perturbação do vento, durante a regeneração. Quando as árvores caem, as árvores que elas abrigavam ficam expostas e, por sua vez, são mais propensas a serem danificadas, de modo que as lacunas tendem a se expandir na direção do vento. Enquanto isso, a barlavento, crescem árvores jovens, protegidas pela sombra do vento das árvores altas remanescentes.[35] Os padrões naturais às vezes são formados por animais, como nos montes Mima do noroeste dos Estados Unidos e algumas outras áreas, que parecem ser criados ao longo de muitos anos pelas atividades escavadoras de esquilos de bolso,[36] enquanto os chamados círculos de fadas da Namíbia parece ser criada pela interação de grupos concorrentes de cupins de areia, juntamente com a competição por água entre as plantas do deserto.[37]

Em solos de permafrost com uma camada superior ativa sujeita a congelamento e degelo anual, o solo padronizado pode se formar, criando círculos, redes, polígonos de cunha de gelo, degraus e listras. A contração térmica causa a formação de trincas de retração; no degelo, a água preenche as rachaduras, expandindo-se para formar gelo na próxima vez que congelar e alargando as rachaduras em fatias. Essas rachaduras podem se unir para formar polígonos e outras formas.[38]

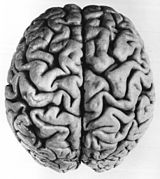
O padrão fissurado que se desenvolve nos cérebros dos vertebrados é causado por um processo físico de expansão restrita dependente de dois parâmetros geométricos: expansão cortical tangencial relativa e espessura relativa do córtex. Padrões semelhantes de giros (picos) e sulcos (depressões) foram demonstrados em modelos do cérebro a partir de géis lisos em camadas, com os padrões causados ​​por forças mecânicas compressivas resultantes da expansão da camada externa (representando o córtex) após o adição de um solvente. Modelos numéricos em simulações de computador suportam observações naturais e experimentais de que os padrões de dobramento da superfície aumentam em cérebros maiores.[39][40]

  • Baiacu-gigante, Tetraodon mbu
    Baiacu-gigante, Tetraodon mbu
  • Detalhe do padrão de pele do baiacu-gigante
    Detalhe do padrão de pele do baiacu-gigante
  • Simulação computacional da reação de Belousov-Zhabotinsky
    Simulação computacional da reação de Belousov-Zhabotinsky
  • Vista aérea de um planalto de mata-tigre no Níger
    Vista aérea de um planalto de mata-tigre no Níger
  • Ondas de abeto em White Mountains, New Hampshire
    Ondas de abeto em White Mountains, New Hampshire
  • Solo padronizado: um pingo derretendo com polígonos de cunha de gelo ao redor perto de Tuktoyaktuk, Canadá
    Solo padronizado: um pingo derretendo com polígonos de cunha de gelo ao redor perto de Tuktoyaktuk, Canadá
  • Círculos de fadas na área na Namíbia
    Círculos de fadas na área na Namíbia
  • Cérebro humano (visão superior) exibindo padrões de giros e sulcos
    Cérebro humano (visão superior) exibindo padrões de giros e sulcos

Referências

  1. ↑ Stevens 1974, p. 3.
  2. ↑ Balaguer, Mark (7 de abril de 2009) [2004]. «Platonism in Metaphysics». Stanford Encyclopedia of Philosophy. Consultado em 4 de maio de 2012 
  3. ↑ a b c d e Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number First trade paperback ed. New York: Broadway Books. p. 110. ISBN 978-0-7679-0816-0 
  4. ↑ Da Vinci, Leonardo (1971). Taylor, Pamela, ed. The Notebooks of Leonardo da Vinci. [S.l.]: New American Library. p. 121 
  5. ↑ Singh, Parmanand (1986). «Acharya Hemachandra and the (so called) Fibonacci Numbers». Mathematics Education Siwan. 20 (1): 28–30. ISSN 0047-6269 
  6. ↑ Knott, Ron. «Fibonacci's Rabbits». University of Surrey Faculty of Engineering and Physical Sciences 
  7. ↑ Browne, Thomas (1658). How Nature Geometrizeth. The Garden of Cyrus. [S.l.: s.n.] 
  8. ↑ Padovan, Richard (1999). Proportion: Science, Philosophy, Architecture. [S.l.]: Taylor & Francis. pp. 305–306. ISBN 978-0-419-22780-9 
  9. ↑ Padovan, Richard (2002). «Proportion: Science, Philosophy, Architecture». Nexus Network Journal. 4 (1): 113–122. doi:10.1007/s00004-001-0008-7Acessível livremente 
  10. ↑ Zeising, Adolf (1854). Neue Lehre van den Proportionen des meschlischen Körpers. [S.l.: s.n.] preface 
  11. ↑ Stewart 2001, pp. 108–109.
  12. ↑ Ball 2009a, pp. 73–76.
  13. ↑ Hannavy, John (2007). Encyclopedia of Nineteenth-Century Photography. 1. [S.l.]: CRC Press. p. 149. ISBN 978-0-415-97235-2 
  14. ↑ Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. New York: Broadway Books. p. 111. ISBN 978-0-7679-0816-0 
  15. ↑ About D'Arcy Arquivado em 2017-07-01 no Wayback Machine. D' Arcy 150. University of Dundee and the University of St Andrews. Retrieved 16 October 2012.
  16. ↑ a b Turing, A. M. (1952). «The Chemical Basis of Morphogenesis». Philosophical Transactions of the Royal Society B. 237 (641): 37–72. Bibcode:1952RSPTB.237...37T. doi:10.1098/rstb.1952.0012Acessível livremente 
  17. ↑ Ball 2009a, pp. 163, 247–250.
  18. ↑ a b Rozenberg, Grzegorz; Salomaa, Arto. The Mathematical Theory of L Systems. Academic Press, New York, 1980. ISBN 0-12-597140-0
  19. ↑ Erro de citação: Etiqueta <ref> inválida; não foi fornecido texto para as refs de nome Mandelbrot
  20. ↑ Forbes, Peter. All that useless beauty. The Guardian. Review: Non-fiction. 11 de fevereiro de 2012.
  21. ↑ Stevens 1974, p. 222.
  22. ↑ Steen, L.A. (1988). «The Science of Patterns». Science. 240 (4852): 611–616. Bibcode:1988Sci...240..611S. PMID 17840903. doi:10.1126/science.240.4852.611 
  23. ↑ Devlin, Keith. Mathematics: The Science of Patterns: The Search for Order in Life, Mind and the Universe (Scientific American Paperback Library) 1996
  24. ↑ Tatarkiewicz, Władysław. «Perfection in the Sciences. II. Perfection in Physics and Chemistry». Dialectics and Humanism. 7 (2 (spring 1980)): 139 
  25. ↑ a b Darwin, Charles. On the Origin of Species. 1859, chapter 4.
  26. ↑ Wickler, Wolfgang (1968). Mimicry in plants and animals. New York: McGraw-Hill  Verifique o valor de |url-access=registration (ajuda)
  27. ↑ Poulin, R.; Grutter, A.S. (1996). «Cleaning symbioses: proximate and adaptive explanations». BioScience. 46 (7): 512–517. JSTOR 1312929. doi:10.2307/1312929Acessível livremente 
  28. ↑ Koning, Ross (1994). «Plant Physiology Information Website». Pollination Adaptations. Consultado em 2 de maio de 2012 
  29. ↑ Murray, James D. (9 March 2013). Mathematical Biology. [S.l.]: Springer Science & Business Media. pp. 436–450. ISBN 978-3-662-08539-4  Verifique data em: |data= (ajuda)
  30. ↑ a b Ball 2009a, pp. 159–167.
  31. ↑ Ball 2009a, pp. 168–180.
  32. ↑ Rothenberg 2011, pp. 93–95.
  33. ↑ a b Prum, Richard O.; Williamson, Scott (2002). «Reaction–diffusion models of within-feather pigmentation patterning» (PDF). Proceedings of the Royal Society of London B. 269 (1493): 781–792. PMC 1690965Acessível livremente. PMID 11958709. doi:10.1098/rspb.2001.1896 
  34. ↑ a b Tongway, D. J.; Valentin, C.; Seghieri, J. (2001). Banded vegetation patterning in arid and semiarid environments. New York: Springer-Verlag 
  35. ↑ a b D'Avanzo, C. (22 February 2004). «Fir Waves: Regeneration in New England Conifer Forests». TIEE. Consultado em 26 May 2012  Verifique data em: |acessodata=, |data= (ajuda)
  36. ↑ Morelle, Rebecca (9 de dezembro de 2013). «'Digital gophers' solve Mima mound mystery». BBC News. Consultado em 9 December 2013  Verifique data em: |acessodata= (ajuda)
  37. ↑ Sample, Ian (18 January 2017). «The secret of Namibia's 'fairy circles' may be explained at last». The Guardian. Consultado em 18 January 2017  Verifique data em: |acessodata=, |data= (ajuda)
  38. ↑ «Permafrost: Patterned Ground». US Army Corps of Engineers. Consultado em 17 de fevereiro de 2015. Cópia arquivada em 7 de março de 2015 
  39. ↑ Ghose, Tia. «Human Brain's Bizarre Folding Pattern Re-Created in a Vat». Scientific American. Consultado em 5 de abril de 2018 
  40. ↑ Tallinen, Tuoma; Chung, Jun Young; Biggins, John S.; Mahadevan, L. (2014). «Gyrification from constrained cortical expansion». Proceedings of the National Academy of Sciences of the United States of America. 111 (35): 12667–12672. Bibcode:2014PNAS..11112667T. PMC 4156754Acessível livremente. PMID 25136099. arXiv:1503.03853Acessível livremente. doi:10.1073/pnas.1406015111Acessível livremente 

Bibliografia

Pioneering authors

Busca Wikisource O Wikisource em latin tem texto original relacionado com este artigo:

General books

Patterns from nature (as art)

  • Edmaier, Bernard. Patterns of the Earth. Phaidon Press, 2007.
  • Macnab, Maggie. Design by Nature: Using Universal Forms and Principles in Design. New Riders, 2012.
  • Nakamura, Shigeki. Pattern Sourcebook: 250 Patterns Inspired by Nature.. Books 1 and 2. Rockport, 2009.
  • O'Neill, Polly. Surfaces and Textures: A Visual Sourcebook. Black, 2008.
  • Porter, Eliot e Gleick, James. Nature's Chaos. Viking Penguin, 1990.

Ligações externas

Obtida de "https://pt.wikipedia.org/w/index.php?title=Padrões_na_natureza&oldid=65704786"