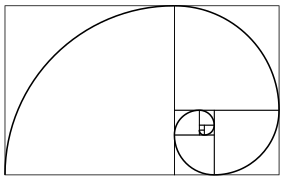
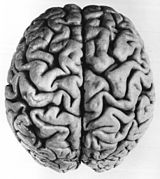
Padrões na natureza

Origem: Wikipédia, a enciclopédia livre.
Padrões naturais se formam quando o vento sopra a areia nas dunas do deserto do Namibe. As dunas em forma de crescente e as ondulações em suas superfícies se repetem onde quer que haja condições adequadas.
Padrões do camaleão velado, Chamaeleo calyptratus, fornecem camuflagem e sinal de humor, bem como condição de reprodução.

Padrões na natureza são regularidades visíveis de forma encontradas no mundo natural. Esses padrões se repetem em diferentes contextos e às vezes podem ser modelizados matematicamente. Padrões naturais incluem simetrias, árvores, espirais, meandros, ondas, espumas, mosaicos, rachaduras e listras.[1] Os primeiros filósofos gregos já haviam estudado essa questão, com Platão, Pitágoras e Empédocles tentando explicar a ordem na natureza. A compreensão moderna dos padrões visíveis desenvolveu-se gradualmente ao longo do tempo.

No século XIX, o físico belga Joseph Plateau examinou películas de sabão, levando-o a formular o conceito de superfície mínima. O biólogo e artista alemão Ernst Haeckel pintou centenas de organismos marinhos para enfatizar sua simetria. O biólogo escocês D'Arcy Thompson foi pioneiro no estudo dos padrões de crescimento em plantas e animais, mostrando que equações simples poderiam explicar o crescimento em espiral. No século XX, o matemático britânico Alan Turing previu mecanismos de morfogênese que dão origem a padrões de manchas e listras. O biólogo húngaro Aristid Lindenmayer e o matemático franco-estadunidense Benoît Mandelbrot mostraram como a matemática dos fractais poderia descrever padrões de crescimento de plantas.

A matemática, a física e a química procuram explicar padrões na natureza em diferentes níveis e escalas. Os padrões em seres vivos são explicados pelos processos biológicos de seleção natural e seleção sexual. Estudos de formação de padrões fazem uso de modelos computacionais para simular uma ampla gama de padrões.

História[editar | editar código-fonte]

Os primeiros filósofos gregos tentaram explicar a ordem na natureza, antecipando conceitos modernos. Pitágoras explicou os padrões da natureza, como as harmonias musicais, como decorrentes das propriedades número, que ele considerava o constituinte básico da existência. Empédocles antecipou até certo ponto a explicação evolutiva de Darwin para as estruturas dos organismos. Platão defendeu a tese de universais naturais. Ele considerou que estes consistiam em formas ideais (εἶδος eidos: "forma"), e os objetos físicos nada mais são que cópias imperfeitas. Assim, uma flor pode ser aproximadamente circular, mas nunca é um círculo perfeito.[2] Teofrasto observou que as plantas "que têm folhas planas as têm em uma série regular"; Plínio, o Velho notou seu arranjo circular padronizado.[3] Séculos depois, Leonardo da Vinci notou o arranjo espiral dos padrões das folhas, que os troncos das árvores ganham anéis sucessivos à medida que envelhecem e propôs uma regra supostamente satisfeita para as áreas transversais dos galhos das árvores.[3][4]

Em 1202, Leonardo Fibonacci introduziu a sequência de Fibonacci em seu livro Liber Abaci.[5] Fibonacci apresentou um experimento mental sobre o crescimento de uma população ideal de coelhos.[6] Johannes Kepler apontou a presença da sequência de Fibonacci na natureza, usando-a para explicar a forma pentagonal de algumas flores.[3] Em 1658, o médico e filósofo inglês Thomas Browne discutiu "como a natureza geometriza" em The Garden of Cyrus, citando a numerologia pitagórica envolvendo o número 5 e a forma platônica do padrão quincunce.[7] Em 1754, Charles Bonnet observou que a filotaxia espiral das plantas era frequentemente expressa em séries de proporção áurea no sentido horário e anti-horário.[3] Observações matemáticas da filotaxia seguiram-se com os trabalhos de Karl Friedrich Schimper e seu amigo Alexander Braun; Augusto Bravaise e seu irmão Louis conectou as taxas de filotaxia à sequência de Fibonacci em 1837, também observando sua aparência em pinhas e abacaxis.[3] Em seu livro de 1854, o psicólogo alemão Adolf Zeising explorou a proporção áurea expressa no arranjo das partes das plantas, nos esqueletos dos animais e nos padrões de ramificação de suas veias e nervos, bem como nos cristais.[8][9][10]

No século XIX, o físico belga Joseph Plateau formulou o problema matemático da existência de uma superfície mínima com um determinado limite. Ele estudou intensamente as películas de sabão, formulando as leis de Plateau, que descrevem as estruturas formadas por filmes em espumas.[11] William Thomson identificou o problema da maneira mais eficiente de embalar células de igual volume como uma espuma em 1887; sua solução usa apenas um sólido, o favo de mel cúbico bitruncado com faces ligeiramente curvas para atender às leis de Plateau. Nenhuma solução melhor foi encontrada até 1993, quando Denis Weaire e Robert Phelan propuseram a estrutura de Weaire-Phelan; o Centro Aquático Nacional de Pequim adaptou a estrutura para sua parede externa nos Jogos Olímpicos de Verão de 2008.[12] O fotógrafo americano Wilson Bentley tirou a primeira micrografia de um floco de neve em 1885.[13]

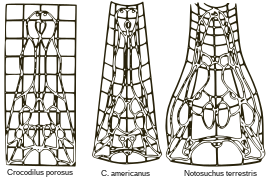
No século XX, A. H. Church estudou os padrões de filotaxia em seu livro de 1904.[14] Em 1917, D'Arcy Wentworth Thompson publicou On Growth and Form; sua descrição da filotaxia e da sequência de Fibonacci, as relações matemáticas nos padrões de crescimento espiral das plantas mostraram que equações simples poderiam descrever os padrões de crescimento espiral de chifres de animais e conchas de moluscos.[15] Em 1952, o cientista da computação Alan Turing escreveu "The Chemical Basis of Morphogenesis", uma análise dos mecanismos que seriam necessários para criar padrões em organismos vivos, no processo chamado morfogênese.[16] Ele previu reações químicas oscilantes, em particular a reação de Belousov-Zhabotinsky. Esses mecanismos de ativação-inibição podem, sugeriu Turing, gerar padrões (chamados padrões de Turing) de listras e manchas em animais e contribuir para os padrões espirais vistos na filotaxia vegetal.[17] Em 1968, o biólogo teórico húngaro Aristid Lindenmayer desenvolveu o sistema-L, uma gramática formal que pode ser usada para modelizar padrões de crescimento de plantas no estilo de fractais.[18] Os sistemas-L têm um alfabeto de símbolos que podem ser combinados usando regras de produção para construir sequências maiores de símbolos e um mecanismo para traduzir as sequências geradas em estruturas geométricas. Em 1975, após séculos de lento desenvolvimento da matemática dos padrões por Gottfried Leibniz, Georg Cantor, Helge von Koch, Wacław Sierpiński e outros, Benoît Mandelbrot escreveu um artigo de larga repercussão, "How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension", cristalizando o pensamento matemático no conceito de fractal.[19]

Causas[editar | editar código-fonte]

Padrões compostos: pulgões e filhotes recém-nascidos em aglomerados em forma de matriz na folha de sicômoro, divididos em polígonos por veias, que são evitados pelos pulgões jovens.

Seres vivos como orquídeas, beija-flores e a cauda do pavão têm desenhos abstratos com forma, padrão e cor que são considerados por muitos como belo, como algo a ser alcançado pela arte.[20] A beleza que as pessoas percebem na natureza tem causas em diferentes níveis, notadamente na matemática que governa quais padrões podem se formar fisicamente, e entre os seres vivos nos efeitos da seleção natural, que governam como os padrões evoluem.[21]

A matemática procura descobrir e explicar padrões abstratos ou regularidades de todos os tipos.[22][23] Padrões visuais na natureza encontram explicações na teoria do caos, fractais, espirais logarítmicas, topologia e outros padrões matemáticos. Por exemplo, os sistemas-L formam modelos convincentes de diferentes padrões de crescimento de árvores.[18]

As leis da física aplicam as abstrações da matemática ao mundo real, muitas vezes como se fosse perfeito. Por exemplo, um cristal é perfeito quando não apresenta defeitos estruturais, como discordâncias, e é totalmente simétrico. A perfeição matemática exata só pode aproximar objetos reais.[24] Padrões visíveis na natureza são governados por leis físicas; por exemplo, os meandros podem ser explicados usando a dinâmica de fluidos.

Em biologia, a seleção natural pode causar o desenvolvimento de padrões nos seres vivos por várias razões, incluindo camuflagem,[25] seleção sexual,[25] e diferentes tipos de sinalização, incluindo mimetismo[26] e simbiose de limpeza.[27] Nas plantas, as formas, cores e padrões de flores polinizadas por insetos, como o lírio, evoluíram para atrair insetos como as abelhas. Padrões radiais de cores e listras, alguns visíveis apenas na luz ultravioleta, servem como guias de néctar que pode ser visto à distância.[28]

Tipos de padrão[editar | editar código-fonte]

Simetria[editar | editar código-fonte]

Ver também: Simetria floral e estrutura cristalina

A simetria é difundida nos seres vivos. Os animais têm principalmente simetria bilateral ou espelhada, assim como as folhas das plantas e algumas flores, como as orquídeas.[29] As plantas geralmente têm simetria radial ou rotacional, assim como muitas flores e alguns grupos de animais, como anêmonas-do-mar. A simetria quíntupla é encontrada nos equinodermos, o grupo que inclui as estrelas-do-mar, ouriços-do-mar e lírios-do-mar.[30]

Entre a matéria não viva, os flocos de neve têm uma notável simetria sêxtupla; a estrutura de cada floco forma um registro das condições variadas durante sua cristalização, com quase o mesmo padrão de crescimento em cada um de seus seis braços.[31] Os cristais em geral têm uma variedade de simetrias e hábitos cristalinos; eles podem ser cúbicos ou octaédricos, mas os cristais verdadeiros não podem ter simetria quíntupla (ao contrário dos quasicristais).[32] A simetria rotacional é encontrada em diferentes escalas entre os seres não vivos, incluindo o padrão de respingos em forma de coroa formado quando uma gota cai em um lago e o formato e anéis esferoidais de um planeta como Saturno.[33]

A simetria tem uma variedade de causas. A simetria radial é adequada para organismos como anêmonas-do-mar, cujos adultos não se movem: alimentos e ameaças podem chegar de qualquer direção. Mas os animais que se movem em uma direção necessariamente têm lados superior e inferior, extremidades da cabeça e da cauda e, portanto, um lado esquerdo e direito. A cabeça torna-se especializada com uma boca e órgãos dos sentidos (cefalização), e o corpo torna-se bilateralmente simétrico (embora os órgãos internos não precisem ser).[34] Mais intrigante é a razão para a simetria quíntupla (pentarradiada) dos equinodermos. Os primeiros equinodermos eram bilateralmente simétricos, como suas larvas ainda são. Sumrall e Wray argumentam que a perda da velha simetria teve causas de desenvolvimento e ecológicas.[35]

Árvores e fractais[editar | editar código-fonte]

O padrão de ramificação das árvores foi descrito no Renascimento italiano por Leonardo da Vinci. Em seu Trattato della Pittura, afirmou que:

Todos os galhos de uma árvore em cada estágio de sua altura quando colocados juntos são iguais em espessura ao tronco [abaixo deles].[36]

Uma versão mais geral afirma que quando uma ramificação-mãe se divide em duas ou mais ramificações-filhas, as áreas de superfície das ramificações-filhas se somam às da ramificação-mãe.[37] Uma formulação equivalente é que, se um ramo se divide em outros dois, então os diâmetros das seções transversais do original e de seus derivados formam um triângulo retângulo. Uma explicação é que isso permite que as árvores resistam melhor aos ventos fortes.[37] Simulações de modelos biomecânicos corroboram essa tese.[38]

Fractais são construções matemáticas iteradas e infinitamente autossimilares com dimensão fractal.[19][39][40] A iteração infinita não é possível na natureza, então todos os padrões 'fractais' são apenas aproximados. Por exemplo, as folhas de samambaias e umbelíferas são autossimilares (pinadas) apenas em dois, três ou quatro níveis. Padrões de crescimento semelhantes a samambaias ocorrem em plantas e animais, incluindo briozoários, corais, hidrozoários como a samambaia aérea, e em coisas não vivas, principalmente descargas elétricas. Os fractais do sistema-L podem modelar diferentes padrões de crescimento de árvores, variando um pequeno número de parâmetros, incluindo ângulo de ramificação, distância entre nós ou pontos de ramificação e número de ramificações por ponto de ramificação.[18]

Padrões semelhantes a fractais ocorrem amplamente na natureza, em fenômenos tão diversos quanto nuvens, redes fluviais, falhas geológicas, montanhas, litorais,[41] coloração animal, flocos de neve,[42] cristais,[43] ramificação de vasos sanguíneos,[44] células de Purkinje,[45] citoesqueletos de actina[46] e ondas oceânicas.[47]

  • Os padrões de crescimento de certas árvores lembram os fractais do sistema-L
    Os padrões de crescimento de certas árvores lembram os fractais do sistema-L
  • Padrão de ramificação de um baobá
    Padrão de ramificação de um baobá
  • Folha de cicuta, Anthriscus sylvestris
    Folha de cicuta, Anthriscus sylvestris
  • Brócolis romanesco com forma autossimilar
    Brócolis romanesco com forma autossimilar
  • ]] com esferas formadas por outras esferas
    ]] com esferas formadas por outras esferas
  • Figura de Lichtenberg: quebra dielétrica de alta tensão em um bloco de polímero acrílico
    Figura de Lichtenberg: quebra dielétrica de alta tensão em um bloco de polímero acrílico
  • Cristais dendríticos de cobre no microscópio
    Cristais dendríticos de cobre no microscópio

Espirais[editar | editar código-fonte]

Ver também: Filotaxia

As espirais são comuns em plantas e em alguns animais, principalmente moluscos. Por exemplo, no náutilo, um molusco cefalópode, cada câmara de sua concha é uma cópia aproximada da próxima, dimensionada por um fator constante e disposta em uma espiral logarítmica.[48] Dada a compreensão moderna dos fractais, uma espiral de crescimento pode ser vista como um caso especial de autossimilaridade.[49]

As espirais das plantas podem ser vistas na filotaxia, o arranjo das folhas em um caule e no arranjo de outras partes, como em cabeças de flores compostas e cabeças de sementes como o girassol ou estruturas de frutas como o abacaxi e a fruta da serpente,[14][50] bem como no padrão de escamas em pinhas, em que múltiplas espirais correm no sentido horário e anti-horário.[51][52] As espirais da filotaxia podem ser geradas a partir da sequência de Fibonacci: 1, 1, 2, 3, 5, 8, 13... Por exemplo, quando as folhas se alternam em um caule, uma rotação da espiral toca duas folhas, então o padrão ou proporção é 1/2. Na avelã a proporção é de 1/3; no damasco é 2/5; na pera é 3/8; na amêndoa é 5/13.[53]

Na filotaxia de disco, como no girassol e na margarida, as flores são dispostas ao longo da espiral de Fermat, mas isso é disfarçado porque as flores sucessivas são espaçadas, pelo ângulo áureo, 137,508° (dividindo o círculo na proporção áurea); quando a flor está madura e todos os elementos têm o mesmo tamanho, esse espaçamento cria um número Fibonacci de espirais mais óbvias.[54]

Do ponto de vista da física, as espirais são configurações de baixa energia[55] que emergem espontaneamente através de processos auto-organizados em sistemas dinâmicos.[56] Do ponto de vista da química, uma espiral pode ser gerada por um processo de reação-difusão, envolvendo ativação e inibição. A filotaxia é controlada por proteínas que manipulam a concentração do hormônio vegetal auxina, que ativa o crescimento do meristema, juntamente com outros mecanismos para controlar o ângulo relativo das gemas ao redor do caule.[57] Do ponto de vista biológico, dispor as folhas o mais longe possível em qualquer espaço é favorecido pela seleção natural, pois maximiza o acesso aos recursos, especialmente a luz solar para a fotossíntese.[50]

Caos, fluxo e meandros[editar | editar código-fonte]

Em matemática, um sistema dinâmico é caótico se for (altamente) sensível às condições iniciais (o chamado efeito borboleta),[58] que requer as propriedades matemáticas de mistura topológica e órbitas periódicas densas.[59]

Juntamente com os fractais, a teoria do caos se classifica como uma influência essencialmente universal sobre os padrões da natureza. Existe uma relação entre o caos e os fractais – os atratores estranhos em sistemas caóticos têm uma dimensão fractal.[60] Alguns autômatos celulares, conjuntos simples de regras matemáticas que geram padrões, têm comportamento caótico, notadamente a Regra 30 de Stephen Wolfram.[61]

Ruas de vórtice são padrões em ziguezague de vórtices giratórios criados pela separação instável do fluxo de um fluido, na maioria das vezes ar ou água, sobre objetos obstrutivos.[62] O fluxo suave (laminar) começa a se romper quando o tamanho da obstrução ou a velocidade do fluxo se torna grande o suficiente em comparação com a viscosidade do fluido.

Meandros são curvas sinuosas em rios ou outros canais, que se formam como um fluido, na maioria das vezes água. Assim que o caminho é ligeiramente curvo, o tamanho e a curvatura de cada loop aumentam à medida que o fluxo helicoidal arrasta materiais como areia e cascalho através do rio para o interior da curva. A parte externa do loop é deixada limpa e desprotegida, de modo que a erosão acelera, aumentando ainda mais os meandros em um poderoso loop de feedback positivo.[63]

Ondas e dunas[editar | editar código-fonte]

As ondas são perturbações que transportam energia à medida que se movem. As ondas mecânicas se propagam através de um meio – ar ou água, fazendo-o oscilar ao passar.[64] Ondas de vento são ondas de superfície do mar que criam o padrão caótico característico de qualquer grande massa de água, embora seu comportamento estatístico possa ser previsto com modelos computacionais.[65] À medida que as ondas na água ou no vento passam sobre a areia, elas criam padrões de ondulações. Quando os ventos sopram sobre grandes massas de areia, eles criam dunas, às vezes em extensos campos de dunas como no deserto do Taclamacã. As dunas podem formar uma variedade de padrões, incluindo crescentes, linhas retas muito longas, estrelas, cúpulas, parábolas e formas longitudinais.[66]

Barchans ou dunas crescentes são produzidas pela ação do vento na areia do deserto; os dois chifres do crescente e a face deslizante apontam na direção do vento. A areia sopra sobre a face contra o vento, que fica a cerca de 15 graus da horizontal, e cai sobre a face de deslizamento, onde se acumula até o ângulo de repouso da areia, que é de cerca de 35 graus. Quando a face de deslizamento excede o ângulo de repouso, a areia sofre uma avalanche, que é um comportamento não linear: a adição de muitas pequenas quantidades de areia não faz com que nada aconteça, mas a adição de uma pequena quantidade adicional repentinamente causa uma grande avalanche.[67] Além dessa não linearidade, os barchans se comportam como ondas solitárias.[68]

Bolhas e espumas[editar | editar código-fonte]

Uma bolha de sabão forma uma esfera, uma superfície com área mínima — a menor área de superfície possível para o volume encerrado. Duas bolhas juntas constituem uma forma mais complexa: as superfícies externas de ambas as bolhas são esféricas; essas superfícies são unidas por uma terceira superfície esférica à medida que a bolha menor incha ligeiramente a maior.[11]

Uma espuma é uma massa de bolhas; espumas de diferentes materiais ocorrem na natureza. As espumas compostas por películas de sabão obedecem às leis de Plateau, que exigem que três películas de sabão se encontrem em cada aresta a 120° e quatro arestas de sabão se encontrem em cada vértice no ângulo tetraédrico de cerca de 109,5°. As leis de Plateau exigem ainda que as películas sejam suaves e contínuos e tenham uma curvatura média constante em todos os pontos. Por exemplo, uma película pode permanecer quase plano em média ao ser curvado para cima em uma direção enquanto é curvado para baixo em outra direção.[69][70] Estruturas com superfícies mínimas podem ser usadas como tendas.

Na escala das células vivas, os padrões de espuma são comuns; radiolários, espículas de esponjas, exoesqueletos silicoflagelados e o esqueleto de calcita de um ouriço-do-mar, todos se assemelham a moldes minerais de limites de espuma das leis de Plateau.[71][72] O esqueleto do radiolário, forma marinha desenhada por Ernst Haeckel, parece uma esfera composta inteiramente de hexágonos, mas isso é matematicamente impossível. A característica de Euler afirma que, para qualquer poliedro convexo, o número de faces mais o número de vértices (cantos) é igual ao número de arestas mais dois. O resultado dessa fórmula é que qualquer poliedro fechado de hexágonos deve incluir exatamente doze pentágonos, como uma bola de futebol, uma cúpula geodésica ou uma molécula de fulereno. Isso pode ser visualizado observando que uma malha de hexágonos é plana como uma folha de tela de arame, mas cada pentágono adicionado força a malha a dobrar (há menos cantos, então a malha é puxada para dentro).[73]

Tesselação[editar | editar código-fonte]

Ver artigo principal: Tesselação

Mosaicos são padrões formados pela repetição de ladrilhos em uma superfície plana.[74] Embora comuns em arte e design, ladrilhos exatamente repetidos são menos fáceis de encontrar em seres vivos. As células nos ninhos de papel de vespas sociais e as células de cera em favos de mel construídas por abelhas são exemplos bem conhecidos. Entre os animais, peixes ósseos, répteis ou pangolim, ou frutas como a fruta da serpente são protegidos por escamas sobrepostas ou osteodermos, que formam unidades repetitivas mais ou menos exatas, embora muitas vezes as escamas de fato variem continuamente em tamanho. Entre as flores, a cabeça de cobra tem um padrão quadriculado em suas pétalas. As estruturas dos minerais fornecem bons exemplos de arranjos tridimensionais que se repetem regularmente. Apesar das centenas de milhares de minerais conhecidos, existem poucos tipos possíveis de arranjos de átomos em um cristal, definidos pela estrutura cristalina, sistema cristalino e grupo pontual; por exemplo, existem exatamente quatorze redes de Bravais para os sete sistemas de redes no espaço tridimensional.[75]

Rachaduras[editar | editar código-fonte]

As rachaduras são aberturas lineares que se formam nos materiais para aliviar tensões. Quando um material elástico se estica ou encolhe uniformemente, ele finalmente atinge sua resistência à ruptura e então falha repentinamente em todas as direções, criando rachaduras com juntas de 120 graus, de modo que três rachaduras se encontram em um nó. Por outro lado, quando um material inelástico falha, trincas retas se formam para aliviar a tensão. Mais tensão na mesma direção simplesmente abriria as trincas existentes; tensões em ângulos retos podem criar novas trincas, a 90 graus das antigas. Assim, o padrão de fissuras indica se o material é elástico ou não.[76] Em um material fibroso resistente como a casca de carvalho, rachaduras se formam para aliviar o estresse, como de costume, mas não crescem muito, pois seu crescimento é interrompido por feixes de fortes fibras elásticas. Como cada espécie de árvore tem sua própria estrutura nos níveis de célula e de moléculas, cada uma tem seu próprio padrão de divisão em sua casca.[77]

  • Superfície de cerâmica antiga, esmalte branco com rachaduras principalmente de 90°
    Superfície de cerâmica antiga, esmalte branco com rachaduras principalmente de 90°
  • Secagem de lama inelástica no Rann de Kutch com rachaduras principalmente de 90°
    Secagem de lama inelástica no Rann de Kutch com rachaduras principalmente de 90°
  • Gabro nervurado com rachaduras de 90°, perto de Sgurr na Stri, ilha de Skye
    Gabro nervurado com rachaduras de 90°, perto de Sgurr na Stri, ilha de Skye
  • Secagem de lama elástica na Sicília principalmente com fissuras de 120°
    Secagem de lama elástica na Sicília principalmente com fissuras de 120°
  • Basalto resfriado na Calçada dos Gigantes. Rachaduras majoritariamente verticais de 120° criando colunas hexagonais
    Basalto resfriado na Calçada dos Gigantes. Rachaduras majoritariamente verticais de 120° criando colunas hexagonais
  • Tronco de palmeira com rachaduras verticais ramificadas
    Tronco de palmeira com rachaduras verticais ramificadas

Manchas e listras[editar | editar código-fonte]

Leopardos e joaninhas possuem manchas; peixes-anjo e zebras possuem listras.[78] Esses padrões têm uma explicação evolutiva: eles têm funções que aumentam as chances de que a prole do animal padronizado sobreviva para se reproduzir. Uma das funções dos padrões em animais é a camuflagem;[25] por exemplo, um leopardo que é mais difícil de ser visto captura mais presas. Outra função é a sinalização[26] – por exemplo, uma joaninha tem menos probabilidade de ser atacada por pássaros predadores que caçam à vista, se tiver cores fortes de alerta e também se for amarga ou venenosa. Um pássaro jovem pode ver um inseto com padrão de advertência como uma joaninha e tentar comê-lo, mas só fará isso uma vez; muito em breve cuspirá o inseto amargo; as outras joaninhas na área permanecerão imperturbáveis. Os jovens leopardos e joaninhas, herdando genes que de alguma forma criam manchas, sobrevivem. Mas embora esses argumentos evolutivos e funcionais expliquem por que esses animais precisam de seus padrões, eles não explicam como os padrões são formados.[78]

Formação de padrões[editar | editar código-fonte]

Ver artigo principal: Formação de padrões

Alan Turing,[16] e mais tarde o biólogo matemático James Murray,[79] descreveram um mecanismo que cria espontaneamente padrões manchados ou listrados: um sistema de reação-difusão.[80] As células de um organismo jovem têm genes que podem ser ativados por um sinal químico, um morfogênio, resultando no crescimento de um certo tipo de estrutura, por exemplo uma mancha de pele escura. Se o morfogênio estiver presente em todos os lugares, o resultado é uma pigmentação uniforme, como em um leopardo preto. Mas se for distribuído de forma desigual, podem ocorrer manchas ou listras. Turing sugeriu que poderia haver feedback no controle da produção do próprio morfogênio. Isso pode causar flutuações contínuas na quantidade de morfogênio à medida que se difunde pelo corpo. Um segundo mecanismo é necessário para criar padrões de ondas estacionárias (para resultar em manchas ou listras): um inibidor químico que desliga a produção do morfogênio e que se difunde pelo corpo mais rapidamente do que o morfogênio, resultando em um esquema ativador-inibidor. A reação de Belousov-Zhabotinsky é um exemplo não biológico desse tipo de esquema, um oscilador químico.[80]

Pesquisas posteriores conseguiram criar modelos convincentes de padrões tão diversos quanto listras de zebra, manchas de girafa, manchas de onça e padrões de casca de joaninha.[81] Os modelos de ativação-inibição de Richard Prum, desenvolvidos a partir do trabalho de Turing, usam seis variáveis ​​para explicar o intervalo observado de nove padrões básicos de pigmentação dentro da pena, desde o mais simples, uma mancha de pigmento central, através de manchas concêntricas, barras, divisas, ponto ocular, par de pontos centrais, fileiras de pontos emparelhados e uma matriz de pontos.[82][83] Modelos mais elaborados simulam padrões complexos de penas na galinha-d'angola Numida meleagrisem que as penas individuais apresentam transições de barras na base para uma matriz de pontos na extremidade (distal). Estes requerem uma oscilação criada por dois sinais inibidores, com interações no espaço e no tempo.[83]

Padrões podem se formar por outras razões na paisagem vegetada de mata-tigre[84] e ondas de abetos.[85] Listras de arbustos de tigre ocorrem em encostas áridas, onde o crescimento das plantas é limitado pela chuva. Cada faixa de vegetação mais ou menos horizontal coleta efetivamente a água da chuva da zona nua imediatamente acima dela.[84] Ondas de abeto ocorrem em florestas nas encostas das montanhas após a perturbação do vento, durante a regeneração. Quando as árvores caem, as árvores que elas abrigavam ficam expostas e, por sua vez, são mais propensas a serem danificadas, de modo que as lacunas tendem a se expandir na direção do vento. Enquanto isso, a barlavento, crescem árvores jovens, protegidas pela sombra do vento das árvores altas remanescentes.[85] Os padrões naturais às vezes são formados por animais, como nos montes Mima do noroeste dos Estados Unidos e algumas outras áreas, que parecem ser criados ao longo de muitos anos pelas atividades escavadoras de esquilos de bolso,[86] enquanto os chamados círculos de fadas da Namíbia parece ser criada pela interação de grupos concorrentes de cupins de areia, juntamente com a competição por água entre as plantas do deserto.[87]

Em solos de permafrost com uma camada superior ativa sujeita a congelamento e degelo anual, o solo padronizado pode se formar, criando círculos, redes, polígonos de cunha de gelo, degraus e listras. A contração térmica causa a formação de trincas de retração; no degelo, a água preenche as rachaduras, expandindo-se para formar gelo na próxima vez que congelar e alargando as rachaduras em fatias. Essas rachaduras podem se unir para formar polígonos e outras formas.[88]

O padrão fissurado que se desenvolve nos cérebros dos vertebrados é causado por um processo físico de expansão restrita dependente de dois parâmetros geométricos: expansão cortical tangencial relativa e espessura relativa do córtex. Padrões semelhantes de giros (picos) e sulcos (depressões) foram demonstrados em modelos do cérebro a partir de géis lisos em camadas, com os padrões causados ​​por forças mecânicas compressivas resultantes da expansão da camada externa (representando o córtex) após o adição de um solvente. Modelos numéricos em simulações de computador suportam observações naturais e experimentais de que os padrões de dobramento da superfície aumentam em cérebros maiores.[89][90]

  • Baiacu-gigante, Tetraodon mbu
    Baiacu-gigante, Tetraodon mbu
  • Detalhe do padrão de pele do baiacu-gigante
    Detalhe do padrão de pele do baiacu-gigante
  • Simulação computacional da reação de Belousov-Zhabotinsky
    Simulação computacional da reação de Belousov-Zhabotinsky
  • Vista aérea de um planalto de mata-tigre no Níger
    Vista aérea de um planalto de mata-tigre no Níger
  • Ondas de abeto em White Mountains, New Hampshire
    Ondas de abeto em White Mountains, New Hampshire
  • Solo padronizado: um pingo derretendo com polígonos de cunha de gelo ao redor perto de Tuktoyaktuk, Canadá
    Solo padronizado: um pingo derretendo com polígonos de cunha de gelo ao redor perto de Tuktoyaktuk, Canadá
  • Círculos de fadas na área na Namíbia
    Círculos de fadas na área na Namíbia
  • Cérebro humano (visão superior) exibindo padrões de giros e sulcos
    Cérebro humano (visão superior) exibindo padrões de giros e sulcos

Referências

  1. ↑ Stevens 1974, p. 3.
  2. ↑ Balaguer, Mark (7 de abril de 2009) [2004]. «Platonism in Metaphysics». Stanford Encyclopedia of Philosophy. Consultado em 4 de maio de 2012 
  3. ↑ a b c d e Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number First trade paperback ed. New York: Broadway Books. p. 110. ISBN 978-0-7679-0816-0 
  4. ↑ Da Vinci, Leonardo (1971). Taylor, Pamela, ed. The Notebooks of Leonardo da Vinci. [S.l.]: New American Library. p. 121 
  5. ↑ Singh, Parmanand (1986). «Acharya Hemachandra and the (so called) Fibonacci Numbers». Mathematics Education Siwan. 20 (1): 28–30. ISSN 0047-6269 
  6. ↑ Knott, Ron. «Fibonacci's Rabbits». University of Surrey Faculty of Engineering and Physical Sciences 
  7. ↑ Browne, Thomas (1658). How Nature Geometrizeth. The Garden of Cyrus. [S.l.: s.n.] 
  8. ↑ Padovan, Richard (1999). Proportion: Science, Philosophy, Architecture. [S.l.]: Taylor & Francis. pp. 305–306. ISBN 978-0-419-22780-9 
  9. ↑ Padovan, Richard (2002). «Proportion: Science, Philosophy, Architecture». Nexus Network Journal. 4 (1): 113–122. doi:10.1007/s00004-001-0008-7Acessível livremente 
  10. ↑ Zeising, Adolf (1854). Neue Lehre van den Proportionen des meschlischen Körpers. [S.l.: s.n.] preface 
  11. ↑ a b Stewart 2001, pp. 108–109.
  12. ↑ Ball 2009a, pp. 73–76.
  13. ↑ Hannavy, John (2007). Encyclopedia of Nineteenth-Century Photography. 1. [S.l.]: CRC Press. p. 149. ISBN 978-0-415-97235-2 
  14. ↑ a b Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. New York: Broadway Books. p. 111. ISBN 978-0-7679-0816-0 
  15. ↑ About D'Arcy Arquivado em 2017-07-01 no Wayback Machine. D' Arcy 150. University of Dundee and the University of St Andrews. Retrieved 16 de outubro de 2012.
  16. ↑ a b Turing, A. M. (1952). «The Chemical Basis of Morphogenesis». Philosophical Transactions of the Royal Society B. 237 (641): 37–72. Bibcode:1952RSPTB.237...37T. doi:10.1098/rstb.1952.0012Acessível livremente 
  17. ↑ Ball 2009a, pp. 163, 247–250.
  18. ↑ a b c Rozenberg, Grzegorz; Salomaa, Arto. The Mathematical Theory of L Systems. Academic Press, New York, 1980. ISBN 0-12-597140-0
  19. ↑ a b Mandelbrot, Benoît B. (1983). The fractal geometry of nature. [S.l.]: Macmillan 
  20. ↑ Forbes, Peter. All that useless beauty. The Guardian. Review: Non-fiction. 11 de fevereiro de 2012.
  21. ↑ Stevens 1974, p. 222.
  22. ↑ Steen, L.A. (1988). «The Science of Patterns». Science. 240 (4852): 611–616. Bibcode:1988Sci...240..611S. PMID 17840903. doi:10.1126/science.240.4852.611 
  23. ↑ Devlin, Keith. Mathematics: The Science of Patterns: The Search for Order in Life, Mind and the Universe (Scientific American Paperback Library) 1996
  24. ↑ Tatarkiewicz, Władysław. «Perfection in the Sciences. II. Perfection in Physics and Chemistry». Dialectics and Humanism. 7 (2 (spring 1980)): 139 
  25. ↑ a b c Darwin, Charles. On the Origin of Species. 1859, chapter 4.
  26. ↑ a b Wickler, Wolfgang (1968). Mimicry in plants and animals. New York: McGraw-Hill  Verifique o valor de |url-access=registration (ajuda)
  27. ↑ Poulin, R.; Grutter, A.S. (1996). «Cleaning symbioses: proximate and adaptive explanations». BioScience. 46 (7): 512–517. JSTOR 1312929. doi:10.2307/1312929Acessível livremente 
  28. ↑ Koning, Ross (1994). «Plant Physiology Information Website». Pollination Adaptations. Consultado em 2 de maio de 2012 
  29. ↑ Stewart 2001, pp. 48–49.
  30. ↑ Stewart 2001, pp. 64–65.
  31. ↑ Stewart 2001, p. 52.
  32. ↑ Stewart 2001, p. 60.
  33. ↑ Stewart 2001, p. 71.
  34. ↑ Hickman, Cleveland P.; Roberts, Larry S.; Larson, Allan (2002). «Animal Diversity» (PDF). Chapter 8: Acoelomate Bilateral Animals Third ed. 139 páginas. Consultado em 25 de outubro de 2012. Cópia arquivada (PDF) em 17 de maio de 2016 
  35. ↑ Sumrall, Colin D.; Wray, Gregory A. (Janeiro de 2007). «Ontogeny in the fossil record: diversification of body plans and the evolution of "aberrant" symmetry in Paleozoic echinoderms». Paleobiology. 33 (1): 149–163. JSTOR 4500143. doi:10.1666/06053.1 
  36. ↑ Richter, Jean Paul, ed. (1970) [1880]. The Notebooks of Leonardo da Vinci. Dover: [s.n.] ISBN 978-0-486-22572-2 
  37. ↑ a b Palca, Joe (26 de dezembro de 2011). «The Wisdom of Trees (Leonardo Da Vinci Knew It)». Morning Edition. NPR. Consultado em 16 de julho de 2019 
  38. ↑ Minamino, Ryoko; Tateno, Masaki (2014). «Tree Branching: Leonardo da Vinci's Rule versus Biomechanical Models». PLoS One. 9 (4). p. e93535. doi:10.1371/journal.pone.0093535Acessível livremente 
  39. ↑ Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. [S.l.]: John Wiley 
  40. ↑ Briggs, John (1992). Fractals:The Patterns of Chaos. [S.l.]: Thames and Hudson. p. 148 
  41. ↑ Batty, Michael (4 de abril de 1985). «Fractals – Geometry Between Dimensions». New Scientist. 105 (1450): 31 
  42. ↑ Meyer, Yves; Roques, Sylvie (1993). Progress in wavelet analysis and applications: proceedings of the International Conference "Wavelets and Applications," Toulouse, France – June 1992. [S.l.]: Atlantica Séguier Frontières. p. 25. ISBN 9782863321300 
  43. ↑ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw (2000). Pattern formation in biology, vision and dynamics. [S.l.]: World Scientific. p. 78. ISBN 978-9810237929 
  44. ↑ Hahn, Horst K.; Georg, Manfred; Peitgen, Heinz-Otto (2005). «Fractal aspects of three-dimensional vascular constructive optimization». In: Losa, Gabriele A.; Nonnenmacher, Theo F. Fractals in biology and medicine. [S.l.]: Springer. pp. 55–66 
  45. ↑ Takeda, T; Ishikawa, A; Ohtomo, K; Kobayashi, Y; Matsuoka, T (Fevereiro de 1992). «Fractal dimension of dendritic tree of cerebellar Purkinje cell during onto- and phylogenetic development». Neurosci Research. 13 (1): 19–31. PMID 1314350. doi:10.1016/0168-0102(92)90031-7 
  46. ↑ Sadegh, Sanaz (2017). «Plasma Membrane is Compartmentalized by a Self-Similar Cortical Actin Meshwork». Physical Review X. 7 (1): 011031. Bibcode:2017PhRvX...7a1031S. PMC 5500227Acessível livremente. PMID 28690919. arXiv:1702.03997Acessível livremente. doi:10.1103/PhysRevX.7.011031 
  47. ↑ Addison, Paul S. (1997). Fractals and chaos: an illustrated course. [S.l.]: CRC Press. pp. 44–46 
  48. ↑ Maor, Eli. e: The Story of a Number. Princeton University Press, 2009. Page 135.
  49. ↑ Ball 2009a, pp. 29–32.
  50. ↑ a b Kappraff, Jay (2004). «Growth in Plants: A Study in Number» (PDF). Forma. 19: 335–354 
  51. ↑ «Spiral Lattices & Parastichy». Smith College. Consultado em 24 de setembro de 2013. Cópia arquivada em 26 de maio de 2010 
  52. ↑ Ball 2009a, p. 13.
  53. ↑ Coxeter, H. S. M. (1961). Introduction to geometry. [S.l.]: Wiley. 169 páginas 
  54. ↑ Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990). The Algorithmic Beauty of Plants. [S.l.]: Springer-Verlag. pp. 101–107. ISBN 978-0-387-97297-8 
  55. ↑ Levitov, L. S. (15 de março de 1991). «Energetic Approach to Phyllotaxis». Europhysics Letters. 14 (6): 533–539. Bibcode:1991EL.....14..533L. doi:10.1209/0295-5075/14/6/006 
  56. ↑ Douady, S.; Couder, Y. (Março de 1992). «Phyllotaxis as a physical self-organized growth process». Physical Review Letters. 68 (13): 2098–2101. Bibcode:1992PhRvL..68.2098D. PMID 10045303. doi:10.1103/PhysRevLett.68.2098 
  57. ↑ Ball 2009a, pp. 163, 249–250.
  58. ↑ Lorenz, Edward N. (Março de 1963). «Deterministic Nonperiodic Flow». Journal of the Atmospheric Sciences. 20 (2): 130–141. Bibcode:1963JAtS...20..130L. doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2Acessível livremente 
  59. ↑ Elaydi, Saber N. (1999). Discrete Chaos. [S.l.]: Chapman & Hall/CRC. p. 117 
  60. ↑ Ruelle, David (1991). Chance and Chaos. [S.l.]: Princeton University Press 
  61. ↑ Wolfram, Stephen (2002). A New Kind of Science. [S.l.]: Wolfram Media 
  62. ↑ von Kármán, Theodore (1963). Aerodynamics. [S.l.]: McGraw-Hill. ISBN 978-0070676022 . Dover (1994): ISBN 978-0486434858.
  63. ↑ Lewalle, Jacques (2006). «Flow Separation and Secondary Flow: Section 9.1» (PDF). Lecture Notes in Incompressible Fluid Dynamics: Phenomenology, Concepts and Analytical Tools. Syracuse, New York: Syracuse University. Cópia arquivada (PDF) em 29 de setembro de 2011 
  64. ↑ French, A. P. (1971). Vibrations and Waves. [S.l.]: Nelson Thornes 
  65. ↑ Tolman, H. L. (2008). «Practical wind wave modeling» (PDF). In: Mahmood, M.F. CBMS Conference Proceedings on Water Waves: Theory and Experiment. Howard University, USA, 13–18 May 2008. World Scientific Publications 
  66. ↑ «Types of Dunes». USGS. 29 de outubro de 1997. Consultado em 2 de maio de 2012 
  67. ↑ Strahler, A.; Archibold, O. W. (2008). Physical Geography: Science and Systems of the Human Environment 4th ed. [S.l.]: John Wiley. p. 442 
  68. ↑ Schwämmle, V.; Herrman, H. J. (11 de dezembro de 2003). «Solitary wave behaviour of sand dunes». Nature. 426 (6967): 619–620. Bibcode:2003Natur.426..619S. PMID 14668849. doi:10.1038/426619a 
  69. ↑ Ball 2009a, p. 68.
  70. ↑ Almgren, Frederick J. Jr.; Taylor, Jean E. (Julho de 1976). «The geometry of soap films and soap bubbles». Scientific American. 235 (235): 82–93. Bibcode:1976SciAm.235a..82A. doi:10.1038/scientificamerican0776-82 
  71. ↑ Ball 2009a, pp. 96–101.
  72. ↑ Brodie, Christina (Fevereiro de 2005). «Geometry and Pattern in Nature 3: The holes in radiolarian and diatom tests». Microscopy-UK. Consultado em 28 de maio de 2012 
  73. ↑ Ball 2009a, pp. 51–54.
  74. ↑ Armstrong, M.A. (1988). Groups and Symmetry. New York: Springer-Verlag 
  75. ↑ Hook, J. R.; Hall, H. E. Solid State Physics (2nd Edition). Manchester Physics Series, John Wiley & Sons, 2010. ISBN 978-0-471-92804-1
  76. ↑ Stevens 1974, p. 207.
  77. ↑ Stevens 1974, p. 208.
  78. ↑ a b Ball 2009a, pp. 156–158.
  79. ↑ Murray, James D. (9 de março de 2013). Mathematical Biology. [S.l.]: Springer Science & Business Media. pp. 436–450. ISBN 978-3-662-08539-4 
  80. ↑ a b Ball 2009a, pp. 159–167.
  81. ↑ Ball 2009a, pp. 168–180.
  82. ↑ Rothenberg 2011, pp. 93–95.
  83. ↑ a b Prum, Richard O.; Williamson, Scott (2002). «Reaction–diffusion models of within-feather pigmentation patterning» (PDF). Proceedings of the Royal Society of London B. 269 (1493): 781–792. PMC 1690965Acessível livremente. PMID 11958709. doi:10.1098/rspb.2001.1896 
  84. ↑ a b Tongway, D. J.; Valentin, C.; Seghieri, J. (2001). Banded vegetation patterning in arid and semiarid environments. New York: Springer-Verlag 
  85. ↑ a b D'Avanzo, C. (22 de fevereiro de 2004). «Fir Waves: Regeneration in New England Conifer Forests». TIEE. Consultado em 26 de maio de 2012 
  86. ↑ Morelle, Rebecca (9 de dezembro de 2013). «'Digital gophers' solve Mima mound mystery». BBC News. Consultado em 9 de dezembro de 2013 
  87. ↑ Sample, Ian (18 de janeiro de 2017). «The secret of Namibia's 'fairy circles' may be explained at last». The Guardian. Consultado em 18 de janeiro de 2017 
  88. ↑ «Permafrost: Patterned Ground». US Army Corps of Engineers. Consultado em 17 de fevereiro de 2015. Cópia arquivada em 7 de março de 2015 
  89. ↑ Ghose, Tia. «Human Brain's Bizarre Folding Pattern Re-Created in a Vat». Scientific American. Consultado em 5 de abril de 2018 
  90. ↑ Tallinen, Tuoma; Chung, Jun Young; Biggins, John S.; Mahadevan, L. (2014). «Gyrification from constrained cortical expansion». Proceedings of the National Academy of Sciences of the United States of America. 111 (35): 12667–12672. Bibcode:2014PNAS..11112667T. PMC 4156754Acessível livremente. PMID 25136099. arXiv:1503.03853Acessível livremente. doi:10.1073/pnas.1406015111Acessível livremente 

Bibliografia[editar | editar código-fonte]

Autores pioneiros

Livros em geral

Padrões da natureza (como arte)

  • Edmaier, Bernard. Patterns of the Earth. Phaidon Press, 2007.
  • Macnab, Maggie. Design by Nature: Using Universal Forms and Principles in Design. New Riders, 2012.
  • Nakamura, Shigeki. Pattern Sourcebook: 250 Patterns Inspired by Nature.. Books 1 and 2. Rockport, 2009.
  • O'Neill, Polly. Surfaces and Textures: A Visual Sourcebook. Black, 2008.
  • Porter, Eliot e Gleick, James. Nature's Chaos. Viking Penguin, 1990.

Ligações externas[editar | editar código-fonte]

Obtida de "https://pt.wikipedia.org/w/index.php?title=Padrões_na_natureza&oldid=65705977"