Rotação estelar

Rotação estelar é o movimento angular de uma estrela em torno do seu eixo. A velocidade de rotação pode ser medida a partir do espectro da estrela, ou observando o deslocamento de características distintas em sua superfície.
A rotação estelar produz uma protuberância equatorial causado pela força centrífuga. Como as estrelas não são corpos sólidos, estão sujeitas à rotação diferencial. Assim, o equador da estrela pode adquirir uma velocidade angular diferente daquela das latitudes mais altas. A diferença na velocidade de rotação dentro da mesma estrela pode ter um papel significativo na formação do campo magnético estelar.[1]
O campo magnético da estrela interage com o vento estelar. Como o vento se afasta da estrela, sua velocidade angular diminui. A interação entre o campo magnético e o vento estelar é criar uma resistência à rotação estelar. Como resultado, há uma transferência de momento angular da estrela para o vento, que ao longo do tempo, gradualmente reduz a velocidade de rotação da estrela.
Medição[editar | editar código-fonte]
A menos que uma estrela esteja sendo observada na direção do seu polo, diferentes seções de sua superfície mostram algum movimento em direção ou para longe do observador. O componente de movimento em direção ao observador é chamado de velocidade radial. No que tange à parte da superfície com uma componente de velocidade radial na direção do observador, a radiação muda para uma frequencia maior, devido ao efeito Doppler. Também na região, há um componente que se distancia do observador e provoca uma diminuição na frequência. Ao observar a linhas de absorção de uma estrela, esta mudança de frequência no final de um espectro provoca um alargamento na linha.[2] No entanto, essa expansão deve ser estudada com cuidado, pois outros fatores também aumentam a largura da linhas.
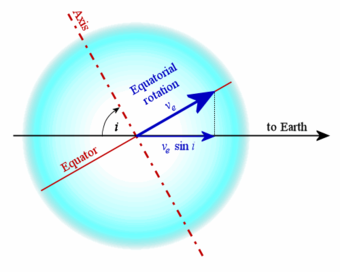
O componente de velocidade radial observada através do alargamento da pela linha depende da inclinação do eixo da estrela para a linha de visão. Este valor é dado por onde ve e é a velocidade de rotação no equador, e i é a inclinação. Mas i nem sempre é conhecida, assim, em muitos casos, só se sabe o valor mínimo para a velocidade de rotação da estrela. Isto é, se i não é um ângulo reto, então a velocidade real é maior do que .[2] Este valor é conhecido como a velocidade de rotação projetada.
Em estrelas gigantes, a microturbulência atmosférica pode produzir uma ampliação nas linhas muito maior do que seria atribuível à rotação, mascarando o sinal. No entanto, há uma outra maneira de abordar o problema fazendo uso do efeito de microlente gravitacional. Isto ocorre quando um objeto massivo passa em frente de uma estrela mais distante, funcionando como uma lente, aumentando a imagem por um curto período. Quanto mais detalhada a informação recolhida durante o evento, mais fácil fica distinguir os efeitos da microturbulência da rotação.[3]
Além disso, se uma estrela mostra a atividade na superfície, como as manchas estelares, esses recursos podem ser utilizados para estimar o período de rotação. No entanto, essas manchas podem se formar em diferentes posições para o equador e, em seguida, migrar ao longo de latitudes diferentes no decorrer de sua vida, é por isso que a rotação diferencial de uma estrela pode levar a medidas díspares. Uma vez que a atividade magnética estelar, muitas vezes está associada a altas velocidades, esta técnica pode ser usada para estrelas com estas características.[4] O estudo de manchas estelares tem mostrado que, de fato, elas podem provocar variação na velocidade de rotação estelar porque o fluxo de gás é alterado pelo campo magnético.[5]
Efeitos físicos[editar | editar código-fonte]
Protuberância equatorial[editar | editar código-fonte]
A rotação estelar gera uma força centrífuga perpendicular ao eixo. No polo, onde a força centrífuga é zero, a força gravitacional da estrela não tem oposição. No entanto, sob a força centrífuga do equador, ela é diferente de zero e em parte se opõe à força gravitacional. Para equilibrar a diferença de força resultante entre o polo e o equador, a superfície da estrela se expande ao longo do equador fazendo com que a estrela adquira a forma de um esferoide oblato. Esta deformação também causa um escurecimento gravitacional no equador, descrito pelo teorema de von Zeipel.
Um exemplo extremo de protuberância equatorial ocorre na estrela Regulus A (α Leonis A) cujo período de rotação é de 15,9 horas, e a velocidade de rotação como no equador é 317 ± 3 km / s, o equivalente a 86% da velocidade necessária para que a estrela entre em colapso. O raio equatorial da estrela é 32% maior que o raio polar.[6] Outras estrelas que giram rapidamente são Vega, α Arae e Achernar (α Eridani).
A taxa de decaimento de uma estrela é um termo usado para descrever o caso em que a força centrífuga no equador é igual à força gravitacional. Para uma estrela estável, sua rotação deve ser inferior a este valor.[7]
Rotação diferencial[editar | editar código-fonte]
Em estrelas como o Sol, a rotação diferencial existe quando a velocidade angular varia com de acordo com a latitude. Embora geralmente a velocidade angular diminua com a latitude crescente, também tem sido observado o oposto, como na estrela HD 31993.[8][9] AB Doradus é a primeira estrela, fora o Sol, cujo mapa de rotação estelar foi elaborado em detalhe.[10] [11]
O mecanismo subjacente causador da rotação diferencial é a convecção turbulenta no interior da estrela. O movimento de convecção traz energia para a superfície através do movimento do plasma. Esta massa de plasma remove parte da velocidade angular da estrela. Quando a turbulência ocorre através do cisalhamento e da rotação, o momento angular pode ser redistribuído por latitudes diversas por meio do fluxo meridional.[12][13]
Pensa-se que a interface entre as regiões com diferenças marcantes em sua rotação constituam regiões ótimas para os processos dinâmicos que geram o campo magnético estelar. Há também uma interação complexa entre a distribuição de rotação de uma estrela e um campo magnético, a conversão de energia magnética em energia cinética, mudando a distribuição da velocidade.[10]
Diminuição da velocidade de rotação[editar | editar código-fonte]
As estrelas se formam pelo colapso gravitacional de uma nuvem de gás e poeira a baixas temperaturas. Durante o colapso da nuvem, a conservação do momento angular faz com que qualquer pequena rotação das nuvens aumente, restringindo a área em um disco em rotação. No centro do disco denso forma-se uma protoestrela cuja temperatura é aumentada pela energia gravitacional de um colapso.
Na medida em que o colapso continua, a velocidade de rotação pode ser aumentada para um ponto em que a protoestrela em acreção se divida devido à força centrífuga no equador. Assim, para evitar esse cenário, a velocidade de rotação deve desacelerar durante os primeiros 150 mil anos. Uma possível explicação para essa desaceleração é a interação entre o campo magnético estelar e o vento estelar. Neste caso, o vento em expansão elimina o momento angular, diminuindo a rotação da protoestrela.[14][15]
| Classe estelar |
ve (km/s) |
|---|---|
| O5 | 190 |
| B0 | 200 |
| B5 | 210 |
| A0 | 190 |
| A5 | 160 |
| F0 | 95 |
| F5 | 25 |
| G0 | 12 |
Descobriu-se que a maioria das estrelas da sequência principal do tipo espectral entre O5 e F5 giram rapidamente.[6][17] Dentro desse grupo de estrelas, a velocidade de rotação aumenta à medida que a massa atinge valores máximos em estrelas jovens e massivas do tipo B. Como o tempo de vida estimado de uma estrela diminui com o aumento de massa, isso pode ser explicado por uma diminuição na taxa de rotação com a idade.
Para estrelas da sequência principal, a desaceleração na rotação pode ser aproximada pela seguinte relação matemática:
onde é a velocidade angular do equador e t é a idade da estrela.[18] Esta relação é chamada de lei de Skumanich, em homenagem ao astrofísico Andrew P. Skumanich, que a descobriu em 1972.[19] Girocronologia é a disciplina que determina a idade de uma estrela baseando-se em sua velocidade de rotação.[20]
As estrelas perdem massa lentamente pela emissão de vento estelar da fotosfera. O campo magnético da estrela exerce um impulso sobre a matéria ejetada, causando uma perda constante de momento angular pela estrela. Estrelas com uma velocidade de rotação superior a 15 km/s mostram uma maior perda de massa e, portanto, mostram uma desaceleração em sua taxa de decaimento da rotação. Assim, o abrandamento da rotação estelar leva a uma diminuição na taxa de perda de momento angular. Sob essas condições, as estrelas se aproximam gradualmente, mas sem alcançar a condição de .[21]
Estrelas binárias próximas[editar | editar código-fonte]
Uma estrela binária é um sistema onde duas estrelas orbitam uma à outra com uma separação média cuja ordem de grandeza equivale àquela de seus diâmetros. Nessas distâncias, as interações mais complexas acontecem, como forças de maré, transferência de massa e até colisões. Interações gravitacionais num sistema binário muito próximo podem causar mudanças nos parâmetros orbitais e rotacionais, embora o momento angular total do sistema seja conservado, o momento angular de um dos componentes pode ser transferido através do período orbital e da velocidade da rotação.[22]
Cada um dos componentes de em sistema binário próximo provoca marés em sua estrela companheira, devido à atração gravitacional. No entanto, as protuberâncias geradas não podem ser perfeitamente alinhadas com a direção da gravidade, caso em que, a força gravitacional exerce uma componente de impulso, que envolve a transferência de momento angular. Isso provoca uma evolução contínua do sistema, embora possa abordar uma fase de equilíbrio estável. O efeito pode se tornar mais complexo nos casos em que o eixo de rotação não é perpendicular ao plano orbital.[22]
Em binárias de contato ou binárias semisseparadas, a transferência de massa entre os componentes pode resultar também em uma transferência significativa do momento angular. O componente de fase de acreção pode alcançar sua velocidade de rotação crítica começando então a perder a massa sobre o equador.[23]
Estrelas degeneradas[editar | editar código-fonte]
Após o término da fusão termonuclear no interior de uma estrela, ela se transforma em uma estrela compacta composta de matéria degenerada. Durante este processo, as dimensões da estrela são consideravelmente reduzidas, o que pode causar um aumento na velocidade angular.
Anãs brancas[editar | editar código-fonte]
Uma anã branca é uma estrela composta dos produtos sintetizados por fusão termonuclear na etapa anterior de sua vida, mas não possui massa o suficiente para queimar os elementos mais pesados. É um corpo compacto estável cujo colapso gravitacional é evitado por um efeito quântico conhecido como pressão de degeneração eletrônica. Anãs brancas costumam ter uma velocidade de rotação relativamente baixa, seja pelo retardamento da rotação, seja pelo desprendimento do momento angular da estrela progenitora ao perder suas camadas externas [24] (fases de nebulosa protoplanetária e nebulosa planetária).
Uma anã branca girando lentamente não pode exceder o limite de Chandrasekhar de 1,44 massas solares sem entrar em colapso, formando uma estrela de nêutrons ou explodir como uma supernova tipo Ia. Ao atingir essa massa, seja por acréscimo ou colisão, a força gravitacional cede à pressão exercida pelos elétrons. Inversamente, se a anã branca gira rapidamente, a força centrífuga no equador pode compensar a força gravitacional e permitir que sua massa exceda o limite de Chandrasekhar. Esta rotatividade pode surgir, por exemplo, de um aumento de massa que resulta em uma transferência de momento angular.[25]
Estrelas de nêutrons[editar | editar código-fonte]

Uma estrela de nêutrons é um remanescente estelar denso composto principalmente de nêutrons. A massa desses objetos é entre 1,35 e 2,1 massas solares. Como resultado do colapso gravitacional, uma estrela de nêutrons recém-formada pode apresentar uma alta velocidade de rotação da ordem de milhares de rotações por segundo.
Os pulsares são estrelas de nêutrons que giram em alta velocidade e têm um campo magnético intenso. Uma vez que os polos magnéticos emitem um feixe estreito de radiação eletromagnética. Se o feixe de varredura estiver direcionado para o sistema solar, o pulsar produz um pulso periódico que pode ser detectado a partir da Terra. A energia irradiada pelo campo magnético diminui progressivamente a velocidade de rotação, de modo que em pulsares mais velhos que demoram vários segundos entre cada pulso.[26]
Buracos negros[editar | editar código-fonte]
Um buraco negro é um objeto cujo campo gravitacional é grande o suficiente para impedir a fuga da luz. Quando formados pelo colapso de uma massa de rotação, o buraco negro preserva o momento angular, que não é perdido na forma de gás ejetado. Esta rotação faz com que um volume em torno do buraco negro adquira a forma de um esferoide oblato, denominado ergosfera, se desenvolva em torno dele. A massa caindo neste volume ganha energia e uma parte dessa massa pode ser ejetada sem cair no buraco negro. Quando a massa é ejetada, o buraco negro perde o momento angular pelo processo de Penrose.[27] A velocidade de rotação de um buraco negro tem se mostrado ser tão alta quanto 98,7% da velocidade da luz.[28]
Referências
- ↑ Donati, Jean-François (2003). Laboratoire d’Astrophysique de Toulouse, ed. «Differential rotation of stars other than the Sun». Consultado em 24 de junho de 2007
- ↑ a b Shajn, G.; Struve, O. (1929). «On the rotation of the stars». Monthly Notices of the Royal Astronomical Society. 89: 222–239. Bibcode:1929MNRAS..89..222S
- ↑ Gould, Andrew (1997). «Measuring the Rotation Speed of Giant Stars from Gravitational Microlensing». Astrophysical Journal. 483 (1): 98–102. Bibcode:1996astro.ph.11057G. arXiv:astro-ph/9611057
 . doi:10.1086/304244
. doi:10.1086/304244
- ↑ Soon, W.; Frick, P.; Baliunas, S. (1999). «On the rotation of the stars». The Astrophysical Journal. 510 (2): L135–L138. Bibcode:1999ApJ...510L.135S. arXiv:astro-ph/9811114
 . doi:10.1086/311805
. doi:10.1086/311805
- ↑ Collier Cameron, A.; Donati, J.-F. (2002). «Doin' the twist: secular changes in the surface differential rotation on AB Doradus». Monthly Notices of the Royal Astronomical Society. 329 (1): L23–L27. Bibcode:2002MNRAS.329L..23C. arXiv:astro-ph/0111235
 . doi:10.1046/j.1365-8711.2002.05147.x
. doi:10.1046/j.1365-8711.2002.05147.x
- ↑ a b McAlister, H. A., ten Brummelaar, T. A.; et al. (2005). «First Results from the CHARA Array. I. An Interferometric and Spectroscopic Study of the Fast Rotator Alpha Leonis (Regulus).». The Astrophysical Journal. 628 (1): 439–452. Bibcode:2005ApJ...628..439M. arXiv:astro-ph/0501261
 . doi:10.1086/430730
. doi:10.1086/430730
- ↑ Hardorp, J.; Strittmatter, P. A. (8–11 de setembro de 1969). «Rotation and Evolution of be Stars». Proceedings of IAU Colloq. 4. Ohio State University, Columbus, Ohio: Gordon and Breach Science Publishers. p. 48. Bibcode:1970stro.coll...48H
- ↑ Kitchatinov, L. L.; Rüdiger, G. (2004). «Anti-solar differential rotation». Astronomische Nachrichten. 325 (6): 496–500. Bibcode:2004AN....325..496K. arXiv:astro-ph/0504173
 . doi:10.1002/asna.200410297
. doi:10.1002/asna.200410297
- ↑ Ruediger, G.; von Rekowski, B.; Donahue, R. A.; Baliunas, S. L. (1998). «Differential Rotation and Meridional Flow for Fast-rotating Solar-Type Stars». Astrophysical Journal. 494 (2): 691–699. Bibcode:1998ApJ...494..691R. doi:10.1086/305216
- ↑ a b Donati, Jean-François (5 de novembro de 2003). «Differential rotation of stars other than the Sun». Laboratoire d’Astrophysique de Toulouse. Consultado em 24 de junho de 2007
- ↑ Donati, J.-F.; Collier Cameron, A. (1997). «Differential rotation and magnetic polarity patterns on AB Doradus». Monthly Notices of the Royal Astronomical Society. 291 (1): 1–19. Bibcode:1997MNRAS.291....1D
- ↑ Korab, Holly (25 de junho de 1997). «NCSA Access: 3D Star Simulation». National Center for Supercomputing Applications. Consultado em 27 de junho de 2007
- ↑ Küker, M.; Rüdiger, G. (2004). «Differential rotation on the lower main sequence». Astronomische Nachrichten. 326 (3): 265–268. Bibcode:2005AN....326..265K. arXiv:astro-ph/0504411
 . doi:10.1002/asna.200410387
. doi:10.1002/asna.200410387
- ↑ Ferreira, J.; Pelletier, G.; Appl, S. (2000). «Reconnection X-winds: spin-down of low-mass protostars». Monthly Notices of the Royal Astronomical Society. 312 (2): 387–397. Bibcode:2000MNRAS.312..387F. doi:10.1046/j.1365-8711.2000.03215.x
- ↑ Devitt, Terry (31 de janeiro de 2001). «What Puts The Brakes On Madly Spinning Stars?». University of Wisconsin-Madison. Consultado em 27 de junho de 2007
- ↑ McNally, D. (1965). «The distribution of angular momentum among main sequence stars». The Observatory. 85: 166–169. Bibcode:1965Obs....85..166M
- ↑ Peterson, Deane M.; et al. (2004). «Resolving the effects of rotation in early type stars». New Frontiers in Stellar Interferometry, Proceedings of SPIE Volume 5491. Bellingham, Washington, USA: The International Society for Optical Engineering. p. 65. Bibcode:2004SPIE.5491...65P
- ↑ Tassoul, Jean-Louis (1972). Stellar Rotation (PDF). Cambridge, MA: Cambridge University Press. ISBN 0521772184. Consultado em 26 de junho de 2007
- ↑ Skumanich, Andrew P. (1972). «Time Scales for CA II Emission Decay, Rotational Braking, and Lithium Depletion». The Astrophysical Journal. 171: 565. Bibcode:1972ApJ...171..565S. doi:10.1086/151310
- ↑ Barnes, Sydney A. (2007). «Ages for illustrative field stars using gyrochronology: viability, limitations and errors». The Astrophysical Journal. 669 (2): 1167–1189. Bibcode:2007ApJ...669.1167B. arXiv:0704.3068
 . doi:10.1086/519295
. doi:10.1086/519295
- ↑ Nariai, Kyoji (1969). «Mass Loss from Coronae and Its Effect upon Stellar Rotation». Astrophysics and Space Science. 3 (1): 150–159. Bibcode:1969Ap&SS...3..150N. doi:10.1007/BF00649601
- ↑ a b Hut, P. (1999). «Tidal evolution in close binary systems». Astronomy and Astrophysics. 99 (1): 126–140. Bibcode:1981A&A....99..126H
- ↑ Weaver, D.; Nicholson, M. (4 de dezembro de 1997). «One Star's Loss is Another's Gain: Hubble Captures Brief Moment in Life of Lively Duo». NASA Hubble. Consultado em 3 de julho de 2007
- ↑ Willson, L. A.; Stalio, R. (1990). Angular Momentum and Mass Loss for Hot Stars 1st ed. [S.l.]: Springer. pp. 315–16. ISBN 0792308816
- ↑ Yoon, S.-C.; Langer, N. (2004). «Presupernova evolution of accreting white dwarfs with rotation». Astronomy and Astrophysics. 419 (2): 623–644. Bibcode:2004A&A...419..623Y. arXiv:astro-ph/0402287
 . doi:10.1051/0004-6361:20035822
. doi:10.1051/0004-6361:20035822
- ↑ Lorimer, D. R. (28 de agosto de 1998). «Binary and Millisecond Pulsars». Max-Planck-Gesellschaft. Consultado em 26 de julho de 2007. Arquivado do original em 1 de maio de 2012
- ↑ Begelman, Mitchell C. (2003). «Evidence for Black Holes». Science. 300 (5627): 1898–1903. Bibcode:2003Sci...300.1898B. PMID 12817138. doi:10.1126/science.1085334
- ↑ Tune, Lee (29 de maio de 2007). «Spin of Supermassive Black Holes Measured for First Time». University of Maryland Newsdesk. Consultado em 25 de junho de 2007
Ligações externas[editar | editar código-fonte]
- Staff (28 de fevereiro de 2006). «Stellar Spots and Cyclic Activity: Detailed Results». ETH Zürich. Consultado em 22 de outubro de 2009[ligação inativa]




