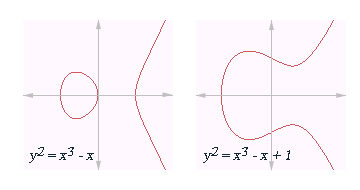Curva elíptica
Este artigo não cita fontes confiáveis. (Julho de 2021) |
Introdução[editar | editar código-fonte]
Em matemática, as curvas elípticas se definem mediante equações cúbicas (de terceiro grau). Têm sido usadas para provar o último teorema de Fermat e se empregam também em criptografia (para mais detalhes pode-se ver o artigo sobre criptografia de curvas elípticas) e em fatoração de inteiros. Estas curvas não são elipses: pode ser visto também o verbete sobre integral elíptica para aprender algo sobre a origem do termo.
As curvas elípticas são "regulares", ou pode-se dizer "não-singulares", o que significa que não têm "cúspides" nem auto-intersecções, e se pode definir uma operação binária para o conjunto de seus pontos de uma maneira geométrica natural, o que faz deste conjunto um grupo abeliano.
As curvas elípticas sobre o corpo dos números reais vêm a ser dadas pelas equações e por .
As curvas elípticas podem definir-se sobre qualquer corpo ; a definição formal de uma curva elíptica é a de uma curva algébrica projetiva não singular sobre de gênero 1. Se a característica de não é nem 2 nem 3, então toda curva elíptica sobre pode escrever-se na forma: , onde e são elementos de tais que o polinômio do membro direito não tenha nenhuma raiz dupla. Se a característica é 2 ou 3 farão falta mais termos.
Sendo assim, vale salientar que há uma forma geral para expressar a equação de uma curva elíptica, a qual é válida para qualquer corpo. Essa forma é conhecida como Equação de Weierstrass e é dada por:
Definição[editar | editar código-fonte]
Normalmente se define a curva como o conjunto de todos os pontos que satisfazem a equação acima e tais que e sejam elementos do fecho algébrico de . Os pontos da curva cujas coordenadas pertençam ambas a se chamam pontos K-racionais.
Se adicionarmos um ponto "ao infinito", obteremos a versão projetiva de tal curva. Se temos dois pontos da curva, e então podemos descrever de forma unívoca um terceiro ponto que seja a intersecção da curva com a linha que atravessa aos dois pontos e . Se a linha é tangente à curva em um ponto, então esse ponto contará duas vezes; e se a linha é paralela ao eixo , definimos o terceiro ponto como o "no" infinito. Então justo uma de tais condições será a que cumpra qualquer par de pontos de uma curva elíptica.
 subgrupo deste grupo.
subgrupo deste grupo.
Se a curva se denota por , este subgrupo se denota normalmente como .
O grupo acima se pode descrever geométrica e algebricamente. Dada a curva sobre o corpo (cuja característica assumimos que não é nem 2 nem 3), e os pontos e na curva, assumimos primeiro que . Seja , já que é um corpo, está bem definido. Então podemos definir mediante
Se , então há duas opções: se , então a soma se define como 0; assim que o inverso de cada ponto da curva se encontra refletindo-o no eixo . Se , então será dado por
Se , então ;
Implicações do teorema de Mordell-Weil[editar | editar código-fonte]
O teorema de Mordell-Weil estabelece que se o corpo subjacente é o dos racionais (ou de maneira mais geral um corpo numérico), então o grupo de pontos -racionais será finitamente gerado. Ainda que se possa determinar facilmente o subgrupo de torsão de , não se conhece um algoritmo geral para computar sua ordem. Uma fórmula para um dado conjunto imagem vem a ser dada pela conjetura de Birch e Swinnerton-Dyer.
Implicações para o último teorema de Fermat[editar | editar código-fonte]
A demonstração recente do último teorema de Fermat se leva a cabo provando um caso especial da profunda conjectura de Taniyama-Shimura que relaciona as curvas elípticas sobre os racionais com as formas modulares; esta conjectura foi também completamente demonstrada.
Se o corpo subjacente é o dos complexos, toda curva elíptica poderá ser parametrizada por certa função elíptica e sua derivada. Especificamente, a cada curva elíptica E se associa um reticulado e uma função elíptica de Weierstrass correspondente , tal que a aplicação
com
seja um isomorfismo de grupos e um isomorfismo de superfícies de Riemann.
O que prova em particular que topologicamente, E assemelha-se a um toro (já que é um toro). Se o reticulado está relacionado com outro reticulado mediante a multiplicação por um número complexo distinto de zero , então as curvas correspondentes são isomorfas. As classes de isomorfismo das curvas elípticas se especificam mediante o j-invariante.
Enquanto que o número de pontos racionais de uma curva elíptica E sobre um corpo finito Fp é difícil de computar em geral, um teorema de Hasse sobre curvas elípticas diz que
Este fato pode entender-se e demostrar-se com algo da teoria geral; ver função zeta local, cohomologia étale.
Para desenvolvimentos posteriores ver aritmética de variedades abelianas.
Teorema de Bezout[editar | editar código-fonte]
Sejam e curvas projetivas planas de graus e definidas sobre um corpo algebricamente fechado. Se e não possuem componentes comuns, então o número de intersecções , contadas com a multiplicidade, é o produto de seus graus, isto é, .
Demonstração: ver [1].
Curvas Elípticas e Teoria dos Grupos[editar | editar código-fonte]
É possível traçar uma relação entre curvas elípticas e a Teoria dos Grupos, conforme mencionado anteriormente. Nesta seção, será introduzida a ideia para demonstrar que uma curva elíptica sobre um corpo é um Grupo abeliano. Para isso, vamos definir uma operação que nos auxiliará para realizar essa demonstração. Sejam e pontos com coordenadas racionais na curva elíptica , e tracemos uma reta que passa por e . Além disso, seja o terceiro ponto ponto de interseção da reta traçada com a curva , conforme a Figura 1 acima.

Agora, vamos definir o , o qual facilmente é provado como elemento neutro. Assim, seja a reta que passa por e e seja o terceiro ponto ponto de interseção com a curva. Seja um ponto tal que a reta que passa por e por intersecta a curva no ponto denotado por . Assim, teremos que . Veja na Figura 2 a seguir.

A partir dessa construção, podemos definir um grupo. Sejam uma curva elíptica sobre um corpo denotada por e . Então, é um grupo abeliano com a operação "+" definida, isto é, satisfaz as seguintes propriedades
- Elemento Neutro: , para todo com coordenadas racionais.
- Inverso: Para todo com coordenadas racionais existe um ponto com coordenadas racionais tal que .
- Associatividade: Sejam , e pontos quaisquer com coordenadas racionais, então .
- Comutatividade: Sejam e pontos quaisquer com coordenadas racionais, então .
A demonstração desse resultado pode ser vista em [2].
Curvas elípticas e criptografia[editar | editar código-fonte]
As curvas elípticas sobre corpos finitos são usadas em algumas aplicações em criptografia assim como na fatoração de inteiros. Uns dos precursores dos estudos relacionando curvas elípticas e criptografia foram Victor Miller e Neal Koblitz. A ideia geral nessas aplicações é que se temos um algoritmo que usa certos grupos finitos podemos reescrevê-lo usando os grupos de pontos racionais de curvas elípticas. Vários são os problemas tópicos relacionados a esse tema, tais como
- O problema do logaritmo discreto em curvas elípticas
- A troca de chaves de Diffie-Hellman com curvas elípticas
- A analogia de Massey-Omura
- A escolha do ponto na curva e seleção "aleatória" de (E, B)
- A redução Global de (E, B)
- Ordem do ponto B
Ver também[editar | editar código-fonte]
Ligações externas[editar | editar código-fonte]
- «The Mathematical Atlas: 14H52 Elliptic Curves» (em inglês)
Sugestões de Leitura[editar | editar código-fonte]
[1] ANDRIA, Sally. e GONDIM, Rodrigo. Criptografia com Curvas Elípticas, 2017 - VIII Bienal da Sociedade Brasileira de Matemática - Rio de Janeiro - RJ. [2] Carneiro, J. S., & Almeida, K. E. de. (2015). Uma Introdução às Curvas Elípticas com Aplicações para o Ensino Médio. Ciência E Natura, 37, 452–462. https://doi.org/10.5902/2179460X14815
[3] FLOSE, Vania Batista Schunck. Criptografia e Curvas Elípticas. 2011. 55 f. Dissertação (Mestrado), Universidade Estadual Paulista, São Paulo, 2011.
Referências[editar | editar código-fonte]
[1] VAINSENCHER, I. Introdução às Curvas Algébricas Planas, Coleção Matemática Universitária, IMPA, Rio de Janeiro, 1996.
[2] Carneiro, J. S., & Almeida, K. E. de. (2015). Uma Introdução às Curvas Elípticas com Aplicações para o Ensino Médio. Ciência E Natura, 37, 452–462. https://doi.org/10.5902/2179460X14815
[3] FLOSE, Vania Batista Schunck. Criptografia e Curvas Elípticas. 2011. 55 f. Dissertação (Mestrado), Universidade Estadual Paulista, São Paulo, 2011.