Conjetura de Goldbach

Ilustração da conjetura de Goldbach.

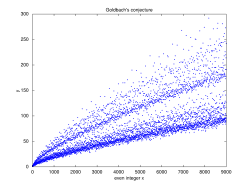
A conjetura de Goldbach, proposta pelo matemático prussiano Christian Goldbach, é um dos problemas mais antigos não resolvidos da matemática, mais precisamente da teoria dos números.

Ela diz que todo número par maior ou igual a 4 é a soma de dois primos.

Por exemplo: 4 = 2 + 2; 6 = 3 + 3; 8 = 5 + 3; 10 = 3 + 7 = 5 + 5; 12 = 5 + 7; etc.

Verificações por computador já confirmaram a conjetura de Goldbach para vários números. No entanto, a efetiva demonstração matemática ainda não ocorreu.

O melhor resultado até agora foi dado por Olivier Ramaré em 1995: todo número par é a soma de até 6 números primos.

Origem

Em 7 de junho de 1742, o matemático prussiano Christian Goldbach escreveu uma carta a Leonhard Euler (carta XLIII) [1], onde ele propôs a seguinte conjetura:

Todo inteiro par maior que 2 pode ser escrito como a soma de 3 números primos. —Goldbach em carta a Euler

Ele considerava o número 1 como sendo primo, que uma convenção posterior (e presente até hoje) abandonou. Uma visão moderna da conjetura (e a mais aceita) é:

Todo inteiro par maior que 5 pode ser escrito como a soma de 3 números primos.

Euler, se interessando pelo problema, respondeu que a conjetura era equivalente à outra:

Todo inteiro par maior que 2 pode ser escrito como a soma de 2 números primos. — Euler respondendo a Goldbach

Euler adicionou, ainda, que estava absolutamente certo sobre isso, porém não era capaz de prová-lo.

A versão de Euler é a mais conhecida e divulgada atualmente, também a mais aceita, por ser mais simples e abrangente.

Resultados numéricos

Para valores pequenos de n, a conjetura de Goldbach pode ser testada diretamente (método conhecido jocosamente pelos matemáticos como força bruta e ignorância ).

Em 1938, N. Pipping testou todos os números até 10⁵.

T. Oliveira e Silva está atualmente testando todos os números até 10¹⁸. .