Vetor (matemática)

 Nota: Para outros significados de vetor, veja Vetor.

Representação gráfica de um vector.

Em geometria analítica, um vetor^(pt-BR) ou vector^(pt-PT?) é uma classe de equipolência de segmentos de reta orientados, que possuem todos a mesma intensidade (denominada norma ou módulo), mesma direção e mesmo sentido. Em alguns casos, a expressão vetor espacial também é utilizada.^{[carece de fontes]}

Neste contexto, um vetor $\mathbf {a}$ pode ser representado por qualquer segmento de reta orientado que seja membro da classe deste vetor (ou seja: pode ser representado por qualquer segmento de reta orientado que possua mesmo módulo, mesma direção e mesmo sentido de qualquer outro segmento da referida classe). E se o segmento ${\overline {AB}}$ (segmento de reta orientado do ponto A para o ponto B) for um representante do vetor $\mathbf {a} ,$ então podemos dizer que o vetor $\mathbf {a}$ é igual ao vetor ${\overrightarrow {AB}}.$

De maneira mais formal, um vetor é definido como sendo uma classe de equipolência de segmentos de reta orientados de $\mathbb {V} ^{n}$, em que $\mathbb {V} ^{n}$ representa um espaço vetorial de n dimensões. Assim sendo, em um espaço vetorial de 3 dimensões ($\mathbb {V} ^{3}$), cada vetor será dotado de três coordenadas, comumente denominadas x, y e z.

Quando falamos em distância geométrica "de A para B", podemos imaginar que o ponto A está sendo "carregado" até chegar ao ponto B

Muitas operações algébricas nos números reais possuem formas análogas para vetores. Vetores podem ser adicionados, subtraídos, multiplicados por um número e invertidos. Essas operações obedecem às conhecidas leis da álgebra: comutatividade, associatividade e distributividade. A soma de dois vetores com o mesmo ponto inicial pode ser encontrada geometricamente usando a regra do paralelogramo. A multiplicação por um número positivo (comumente chamado escalar), nesse contexto, se resume a alterar a magnitude do vetor, isto é, alongando ou encurtando-o porém mantendo o seu sentido. A multiplicação por -1 preserva a magnitude mas inverte o sentido. As coordenadas cartesianas fornecem uma maneira sistemática de descrever e operar vetores.

Os vetores desempenham um papel importante na física: velocidade e aceleração de um objeto e as forças que agem sobre ele são descritas por vetores. É importante ressaltar, no entanto, que os componentes de um vetor físico dependem do sistema de coordenadas usado para descrevê-lo. Outros objetos usados para descrever quantidades físicas são os pseudo-vetores e tensores.

Os vetores têm aplicação em várias áreas do conhecimento, tanto técnico quanto científico, como física, engenharia e economia, por exemplo, sendo os elementos a partir dos quais se constrói o Cálculo Vetorial.

Módulo ou norma do vetor - $||\mathbf {a} ||$

Módulo do vetor é seu comprimento (na figura acima, seria a distância AB).

Fórmula de cálculo (para uma base ortonormal):

$||\mathbf {a} ||={\sqrt {x^{2}+y^{2}+z^{2}}}$ (dedução a partir do Teorema de Pitágoras)

Operações com vetores

Adição vetorial pela regra do paralelogramo.

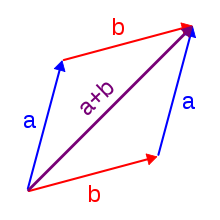
Adição

A decomposição dos vetores em seus componentes horizontais e verticais, nos revela componentes de triângulos retângulos, nos quais podemos observar claramente a propriedade da adição dos vetores.

Observemos o gráfico:

Adição de vetores

Podemos verificar que:

${\vec {w}}={\vec {v}}+{\vec {u}}$

e que:

$w_{x}=v_{x}+u_{x}$

assim como:

$w_{y}=v_{y}+u_{y}.$

Logo temos que, dados dois vetores:

${\vec {v}},{\vec {u}}$

a sua adição resulta em:

${\vec {w}}=\langle v_{x}+u_{x},v_{y}+u_{y}\rangle$

Expandindo para a forma tridimensional temos:

${\vec {w}}=\langle v_{x}+u_{x},v_{y}+u_{y},v_{z}+u_{z}\rangle$

Subtração

Da mesma forma que no caso anterior temos a subtração como já aprendemos, também podemos demonstrar esta propriedade usando a decomposição em triângulos retângulos:

Observemos o gráfico:

Subtração de vetores

Podemos verificar que:

${\vec {w}}={\vec {v}}-{\vec {u}}$

e que:

$w_{x}=v_{x}-u_{x}$

assim como:

$w_{y}=v_{y}-u_{y}.$

Logo temos que, dados dois vetores:

${\vec {v}},{\vec {u}}$

a sua subtração resulta em:

${\vec {w}}=\langle v_{x}-u_{x},v_{y}-u_{y}\rangle$

Expandindo para a forma tridimensional temos:

${\vec {w}}=\langle v_{x}-u_{x},v_{y}-u_{y},v_{z}-u_{z}\rangle$

Multiplicação por escalares

Definimos que se $c\in \mathbb {R}$ expressando apenas valor numérico, então o denominamos escalar.

O produto de um escalar por um vetor é encontrado pela notação:

${\vec {w}}=c\ {\vec {a}}$

que operamos:

${\vec {w}}=\langle c\ a_{x},c\ a_{y},c\ a_{z}\rangle$

onde:

• ${\vec {w}}$ é o vetor resultante;
• ${\vec {a}}$ é o vetor parâmetro original;
• $c$ é o escalar.

Esta operação pode ser observada graficamente ao lado:

Note que todos os vetores gerados pela multiplicação por escalares são paralelos ao original, quando multiplicamos um vetor por $(-1)$ temos uma inversão de sentido e qualquer valor de escalar diferente de $1$ altera a magnitude do vetor.

Produto escalar

O produto escalar, também denominado produto interno, é o produto de dois vetores que resulta em um escalar, a operação que define o seu valor definimos abaixo.

Consideremos dois vetores ${\vec {v}},{\vec {u}},$ cujos componentes são notados por $v_{d}$ e $u_{d}$ respectivamente, sendo $d$ uma das dimensões: $\{x,y,z\},$ então o produto escalar é definido como:

${\vec {v}}\ \cdot \ {\vec {u}}=v_{x}u_{x}+v_{y}u_{y}+v_{z}u_{z}$

Propriedades do produto escalar

As propriedades do produto escalar são facilmente demonstráveis e estão na tabela abaixo, na mesma convencionamos que:

• ${\vec {v}},{\vec {u}},{\vec {w}}$ são vetores em $\mathbb {R} ^{3};$
• $c$ é um escalar.

Propriedade	Operação
Produto nulo	$0\cdot {\vec {v}}=0$
Comutativa do produto escalar	${\vec {v}}\cdot {\vec {u}}={\vec {u}}\cdot {\vec {v}}$
Associativa entre produto escalar e produto por escalares	$c({\vec {v}}\cdot {\vec {u}})=(c{\vec {v}})\cdot {\vec {u}}$
Distributiva	$({\vec {v}}+{\vec {u}})\cdot {\vec {w}}={\vec {v}}\cdot {\vec {w}}+{\vec {u}}\cdot {\vec {w}}$
Escalar quadrado	${\vec {v}}\cdot {\vec {v}}=|{\vec {v}}|^{2}$

A demonstração das propriedades acima fica como exercício, uma vez que todas são intuitivas, não será difícil conseguir demonstrar cada uma delas, para isto basta efetuar a operação do produto escalar e utilizar regras básicas de operações algébricas.

Produto vetorial

As operações com vetores podem, muitas vezes, parecer estranhas a princípio, porém depois que entendemos a sua finalidade e o conceito do fundamento que está por trás de seu comportamento nos habituamos, podendo aproveitar dos recursos que estas operações podem nos oferecer. Um dos cálculos mais intrigantes dentro do universo dos vetores é o chamado produto vetorial, que é definido pela seguinte operação:

Sejam os vetores ${\vec {v}}=\langle v_{x},v_{y},v_{z}\rangle ,{\vec {u}}=\langle u_{x},u_{y},u_{z}\rangle ,$ o produto vetorial dos mesmos é:

${\vec {v}}\times {\vec {u}}=\langle v_{y}u_{z}-u_{y}v_{z},v_{x}u_{z}-u_{x}v_{z},v_{x}u_{y}-u_{x}v_{y}\rangle$

A razão desta definição está na operação geométrica entre dois vetores, que neste caso, objetiva-se em encontrar um vetor que seja, ao mesmo tempo, perpendicular aos dois vetores operados. Como a operação resulta em um novo vetor, ela é denominada de produto vetorial.

A operação resume-se em encontrar coordenadas em cada eixo que sejam perpendiculares entre elas e de módulo igual a área formada pelo paralelogramo criado pela imagem dos dois vetores em cada um dos planos primários.

Podemos observar que cada componente é igual à resultante de um determinante, o que nos habilita representá-los da seguinte forma:

${\vec {v}}\times {\vec {u}}=\left\langle {\begin{vmatrix}v_{y}&v_{z}\\u_{y}&u_{z}\end{vmatrix}},{\begin{vmatrix}v_{x}&v_{z}\\u_{x}&u_{z}\end{vmatrix}},{\begin{vmatrix}v_{x}&v_{y}\\u_{x}&u_{y}\end{vmatrix}}\right\rangle$

Como temos um vetor tridimensional, podemos adotar a notação:

${\vec {v}}\times {\vec {u}}={\begin{vmatrix}v_{y}&v_{z}\\u_{y}&u_{z}\end{vmatrix}}{\vec {i}}+{\begin{vmatrix}v_{x}&v_{z}\\u_{x}&u_{z}\end{vmatrix}}{\vec {j}}+{\begin{vmatrix}v_{x}&v_{y}\\u_{x}&u_{y}\end{vmatrix}}{\vec {k}}$

Que pode ser simplificada ainda mais se adotarmos a notação de determinante com três variáveis:

${\vec {v}}\times {\vec {u}}={\begin{vmatrix}{\vec {i}}&{\vec {j}}&{\vec {k}}\\v_{x}&v_{y}&v_{z}\\u_{x}&u_{y}&u_{z}\end{vmatrix}}$

Em decorrência disto temos um produto que se comporta de maneira idêntica a um determinante, onde todas as propriedades são iguais às apresentadas pelos mesmos.

Propriedades do produto vetorial

O produto vetorial é basicamente uma operação em forma de determinante, a tabela abaixo introduz as propriedades do mesmo, muitas das quais já conhecemos sob a forma de teoremas de determinantes, porém são introduzidas sob a forma de operações vetoriais:

• ${\vec {v}},{\vec {u}},{\vec {w}}$ são vetores em $\mathbb {R} ^{3};$
• $c$ é um escalar.

Propriedade	Operação
Produto vetorial inverso	${\vec {v}}\times {\vec {u}}=-{\vec {u}}\times {\vec {v}}$
múltiplo de escalar por produto vetorial	$c({\vec {v}}\times {\vec {u}})=(c{\vec {v}})\times {\vec {u}}={\vec {v}}\times (c{\vec {u}})$
Distributiva a direita	${\vec {w}}\times ({\vec {v}}+{\vec {u}})={\vec {w}}\times {\vec {v}}+{\vec {w}}\times {\vec {u}}$
Distributiva a esquerda	$({\vec {v}}+{\vec {u}})\times {\vec {w}}={\vec {v}}\times {\vec {w}}+{\vec {u}}\times {\vec {w}}$
Conversão em vetores com produtos escalares	$({\vec {v}}\times {\vec {u}})\times {\vec {w}}=({\vec {v}}\cdot {\vec {w}}){\vec {u}}-({\vec {v}}\cdot {\vec {u}}){\vec {w}}$

Ângulo entre dois vetores

Observemos o gráfico:

Relação entre o ângulo e o produto escalar de dois vetores

Dados dois vetores ${\vec {A}},{\vec {B}},$ é possível demonstrar que o cosseno do ângulo entre os dois vetores é proporcional ao produto interno (escalar), relacionado-se da seguinte forma:

${\vec {A}}\cdot {\vec {B}}=|{\vec {A}}||{\vec {B}}|\cos(\theta )$

Demonstração:

Observemos o gráfico abaixo:

O gráfico mostra dois vetores relacionados pelo ângulo $\theta ,$ é importante notar que temos um triângulo, que pode ser generalizado pela lei dos cossenos, o que nos permite fazer a relação entre o ângulo e os dois vetores.

Considerando os vetores na ilustração acima, podemos fazer o cálculo do módulo de sua diferença, utilizando a conhecida relação da lei dos cossenos para o triângulo:

$|{\vec {v}}-{\vec {u}}|^{2}=|{\vec {v}}|^{2}+|{\vec {u}}|^{2}-2|{\vec {v}}||{\vec {u}}|\cos(\theta )$

$({\vec {v}}-{\vec {u}})\cdot ({\vec {v}}-{\vec {u}})=|{\vec {v}}|^{2}+|{\vec {u}}|^{2}-2|{\vec {v}}||{\vec {u}}|\cos(\theta )$

${\vec {v}}\cdot {\vec {v}}-2{\vec {v}}\cdot {\vec {u}}+{\vec {u}}\cdot {\vec {u}}=|{\vec {v}}|^{2}+|{\vec {u}}|^{2}-2|{\vec {v}}||{\vec {u}}|\cos(\theta )$

$|{\vec {v}}|^{2}+|{\vec {u}}|^{2}-2{\vec {v}}\cdot {\vec {u}}=|{\vec {v}}|^{2}+|{\vec {u}}|^{2}-2|{\vec {v}}||{\vec {u}}|\cos(\theta )$

$-2{\vec {v}}\cdot {\vec {u}}=-2|{\vec {v}}||{\vec {u}}|\cos(\theta )$

Portanto:

${\vec {v}}\cdot {\vec {u}}=|{\vec {v}}||{\vec {u}}|\cos(\theta )$

Relação entre produto vetorial e ângulo entre vetores

Seja os vetores ${\vec {v}}$ e ${\vec {u}}$ vetores em $\mathbb {R} ^{3},$ é possível provar que o módulo do vetor resultante do produto vetorial destes, é proporcional ao seno do ângulo $\theta$ entre os dois vetores, relacionado-se da seguinte forma:

$|{\vec {v}}\times {\vec {u}}|=|{\vec {v}}||{\vec {u}}|\operatorname {sen} (\theta )$ Comprovação: Façamos a operação conforme indicado na definição para verificar a evolução:

${\vec {v}}\times {\vec {u}}=\langle v_{y}u_{z}-u_{y}v_{z},v_{x}u_{z}-u_{x}v_{z},v_{x}u_{y}-u_{x}v_{y}\rangle$

De onde calculamos o seu módulo:

$|{\vec {v}}\times {\vec {u}}|^{2}=(v_{y}u_{z}-u_{y}v_{z})^{2}+(v_{x}u_{z}-u_{x}v_{z})^{2}+(v_{x}u_{y}-u_{x}v_{y})^{2}$

$|{\vec {v}}\times {\vec {u}}|^{2}=v_{y}^{2}u_{z}^{2}-2v_{y}u_{z}u_{y}v_{z}+u_{y}^{2}v_{z}^{2}+v_{x}^{2}u_{z}^{2}-2v_{x}u_{z}u_{x}v_{z}+u_{x}^{2}v_{z}^{2}+v_{x}^{2}u_{y}^{2}-2v_{x}u_{y}u_{x}v_{y}+u_{x}^{2}v_{y}^{2}$

$|{\vec {v}}\times {\vec {u}}|^{2}=(v_{x}^{2}+v_{y}^{2}+v_{z}^{2})(u_{x}^{2}+u_{y}^{2}+u_{z}^{2})-(v_{x}u_{x}+v_{y}u_{y}+v_{z}u_{z})^{2}$

Como já sabemos, podemos aplicar as propriedades já estudadas para os vetores:

$|{\vec {v}}\times {\vec {u}}|^{2}=|{\vec {v}}|^{2}|{\vec {u}}|^{2}-({\vec {v}}\cdot {\vec {v}})^{2}$

$|{\vec {v}}\times {\vec {u}}|^{2}=|{\vec {v}}|^{2}|{\vec {u}}|^{2}-|{\vec {v}}|^{2}|{\vec {u}}|^{2}\cos ^{2}(\theta )$

$|{\vec {v}}\times {\vec {u}}|^{2}=|{\vec {v}}|^{2}|{\vec {u}}|^{2}\left[1-\cos ^{2}(\theta )\right]$

$|{\vec {v}}\times {\vec {u}}|^{2}=|{\vec {v}}|^{2}|{\vec {u}}|^{2}\operatorname {sen} ^{2}(\theta )$

Lembremos que, se:

$a^{2}=\operatorname {sen} ^{2}(\theta ),$

$a=\operatorname {sen} (\theta )$

Quando $0\leq \theta \leq \pi$

logo:

$|{\vec {v}}\times {\vec {u}}|=|{\vec {v}}||{\vec {u}}|\operatorname {sen} (\theta )$

Interpretação do produto vetorial

O vetor resultante do produto vetorial apresenta módulo igual à área do paralelogramo delimitado pelos dois vetores que lhe deram origem, observemos o gráfico abaixo:

Produto vetorial

Como já sabemos, os vetores ${\vec {v}},{\vec {u}}$ que mantêm um ângulo $\theta$ entre eles, quando multiplicados, podem ser expressos desta forma:

$|{\vec {v}}\times {\vec {u}}|=|{\vec {v}}||{\vec {u}}|\operatorname {sen} (\theta )$

Considere a seguinte separação:

$|{\vec {v}}\times {\vec {u}}|=|{\vec {v}}|\ \underbrace {|{\vec {u}}|\operatorname {sen} (\theta )}$

$|{\vec {v}}\times {\vec {u}}|=|{\vec {v}}|\cdot \quad h$

Muito convenientemente, podemos verificar que $h$ é a altura do paralelogramo, que multiplicado pela norma do vetor ${\vec {v}}$ nos dá a área do paralelogramo. Da mesma forma verifiquemos que o produto vetorial nos fornece um vetor perpendicular aos dois que lhe deram origem... Façamos:

$({\vec {v}}\times {\vec {u}})\cdot {\vec {u}}={\begin{vmatrix}{\vec {i}}&{\vec {j}}&{\vec {k}}\\v_{x}&v_{y}&v_{z}\\u_{x}&u_{y}&u_{z}\end{vmatrix}}\cdot \langle v_{x},v_{y},v_{z}\rangle$

Pelas propriedades dos determinantes e do produto escalar temos:

$({\vec {v}}\times {\vec {u}})\cdot {\vec {u}}={\begin{vmatrix}{\vec {i}}v_{x}&{\vec {j}}v_{y}&{\vec {k}}v_{z}\\v_{x}&v_{y}&v_{z}\\u_{x}&u_{y}&u_{z}\end{vmatrix}}$

Sendo o determinante acima nulo, uma vez que uma das suas linhas é múltipla de outra:

$({\vec {v}}\times {\vec {u}})\cdot {\vec {u}}=0$

Também teremos o mesmo resultado para o segundo vetor, visto que o mesmo também é uma das linhas do determinante, portanto o produto vetorial fornece um vetor perpendicular aos dois que lhe deram origem, visto que o cosseno do ângulo $\theta$ é nulo, ou seja, o ângulo é ${\frac {\pi }{2}}.$

Ângulos diretores

A relação entre produto escalar e cosseno do ângulo entre os vetores nos fornece uma outra possibilidade de referenciar os vetores aos eixos do sistema cartesiano, uma vez que temos versores primários para os eixos, podemos verificar qual o resultado do produto escalar entre estes e um vetor qualquer no espaço. Seja o vetor ${\vec {v}}=\langle v_{x},v_{y},v_{z}\rangle ,$ calculemos o produto escalar entre ele e os vetores relacionados aos eixos: $i,j,k:$

${\vec {v}}\cdot i=|{\vec {v}}||i|\cos(\theta )$

$v_{x}=|{\vec {v}}|\cos(\theta )$

${\frac {v_{x}}{|{\vec {v}}|}}=\cos(\theta )$

Para este caso inicialmente façamos uma breve reflexão:

Se para cada vetor de módulo unitário for feita a mesma operação acima, teremos três ângulos para $\theta ,$ os quais são os ângulos do vetor no espaço em relação aos eixos, por esta razão convencionou-se chamá-los de nomes especiais, que são $\alpha ,\beta ,\gamma$ respectivamente, para os vetores $i,j,k.$ Observemos, também, que a operação será sempre a mesma para cada eixo e o resultado será o valor da componente do vetor para o eixo dividido pela norma do mesmo, o que nos fornece três cossenos:

• ${\frac {v_{x}}{|{\vec {v}}|}}=\cos(\alpha )$
• ${\frac {v_{y}}{|{\vec {v}}|}}=\cos(\beta )$
• ${\frac {v_{z}}{|{\vec {v}}|}}=\cos(\gamma )$

Os quais chamamos de cossenos diretores, pois direcionam o vetor no espaço sob a referência dos eixos. Em consequência disto, também chamamos os ângulos de ângulos diretores.

Em conseqüência do que já vimos nas seções anteriores, temos a seguinte equação:

$\cos ^{2}(\alpha )+\cos ^{2}(\beta )+\cos ^{2}(\gamma )=1$

Também temos outra forma de referenciar o vetor, usando os cossenos diretores:

${\vec {v}}=\langle |{\vec {v}}|\cos(\alpha ),|{\vec {v}}|\cos(\beta ),|{\vec {v}}|\cos(\gamma )\rangle$

Que será útil em determinadas análises, inclusive quando parâmetros polares forem considerados.

Projeções sobre vetores

O produto escalar nos dá a possibilidade de encontrar a projeção de um vetor sobre o outro sem a necessidade de sabermos qual o ângulo entre os dois, isto é possível devido à equivalência algébrica do produto escalar com o cosseno do ângulo entre os dois vetores como vimos anteriormente.

Sejam os vetores ${\vec {v}}=\langle v_{x},v_{y},v_{z}\rangle ,{\vec {u}}=\langle u_{x},u_{y},u_{z}\rangle ,$ o produto escalar dos mesmos é:

${\vec {v}}\cdot {\vec {u}}=|{\vec {v}}||{\vec {u}}|\cos(\theta )$

de onde concluimos que:

${\frac {1}{|{\vec {v}}|}}{\vec {v}}\cdot {\vec {u}}=|{\vec {u}}|\cos(\theta )$

$\left({\frac {\vec {v}}{|{\vec {v}}|}}\right)\cdot {\vec {u}}=|{\vec {u}}|\cos(\theta )$

Observando o lado direito da equação observamos que a expressão corresponde à projeção do vetor ${\vec {u}}$ sobre o vetor ${\vec {v}},$ porém sob a forma escalar, ou seja, o valor corresponde ao comprimento (norma) da projeção, não contendo a informação acerca da direção e do sentido. Definimos, então, a projeção escalar do vetor ${\vec {u}}$ sobre o vetor ${\vec {v}},$ como:

$\operatorname {Prj} _{\vec {v}}\ {\vec {u}}=\left({\frac {\vec {v}}{|{\vec {v}}|}}\right)\cdot {\vec {u}}$

Observemos ainda outro fato esclarecedor: a projeção escalar de um vetor sobre o outro é o produto escalar do versor do vetor sobre o qual será projetado e o outro vetor. Intuitivamente, percebemos que o versor que contém a informação sobre a direção e sentido do vetor onde será projetado o valor e portanto, determina-o, visto que é no mesmo onde temos a informação sobre a inclinação.

Seguindo este mesmo raciocínio, se multiplicarmos esta projeção, que é um valor escalar, pelo vetor unitário (versor), que usamos no cálculo anterior, teremos um vetor projeção criado como "imagem" do outro. Fazendo isto teremos:

$V\operatorname {Prj} _{\vec {v}}\ {\vec {u}}=\left({\frac {{\vec {v}}\cdot {\vec {u}}}{|{\vec {v}}|^{2}}}\right){\vec {v}}$

A desigualdade de Cauchy-Schwarz

Sejam os vetores ${\vec {v}}=\langle v_{x},v_{y},v_{z}\rangle ,{\vec {u}}=\langle u_{x},u_{y},u_{z}\rangle ,$ é possível provar que o produto escalar relaciona-se com os módulos dos vetores de forma a satisfazer a seguinte desigualdade

$|{\vec {v}}\cdot {\vec {u}}|\leq |{\vec {v}}||{\vec {u}}|$

Comprovação:

Analisemos o produto escalar ${\vec {v}}\cdot {\vec {u}}$ separadamente:

${\vec {v}}\cdot {\vec {u}}=|{\vec {v}}||{\vec {u}}|\cos(\theta )$

Se quisermos o módulo do produto escalar teremos:

$|{\vec {v}}\cdot {\vec {u}}|=|{\vec {v}}||{\vec {u}}||\cos(\theta )|$

porém,

$0\leq |\cos(\theta )|\leq 1$

então:

$0\leq {\frac {|{\vec {v}}\cdot {\vec {u}}|}{|{\vec {v}}||{\vec {u}}|}}\leq 1$

$0\leq |{\vec {v}}\cdot {\vec {u}}|\leq |{\vec {v}}||{\vec {u}}|$

Como o lado esquerdo da inequação faz parte do módulo, podemos simplificar para:

$|{\vec {v}}\cdot {\vec {u}}|\leq |{\vec {v}}||{\vec {u}}|$

Produto misto

Produto misto

Sejam os vetores ${\vec {v}},{\vec {u}},{\vec {w}}$ em $\mathbb {R} ^{3},$ sobre estes definimos o produto misto como:

$({\vec {v}}\times {\vec {u}})\cdot {\vec {w}}={\begin{vmatrix}w_{x}&w_{y}&w_{z}\\v_{x}&v_{y}&v_{z}\\u_{x}&u_{y}&u_{z}\end{vmatrix}}$

Em síntese, a operação do produto vetorial nos fornece um novo vetor perpendicular aos dois que lhe deram orígem, por outro lado, o produto escalar deste vetor por outro nos fornece um escalar, que representa o produto misto. Observando estas operações mais detalhadamente, quando operamos o produto vetorial temos um vetor definido com os versores primários, sendo ${\vec {v}}\times {\vec {u}}={\vec {p}},$ temos:

${\vec {p}}\cdot {\vec {w}}=(p_{x}i+p_{y}j+p_{z}k)\cdot (w_{x}i+w_{y}j+w_{z}k)$

${\vec {p}}\cdot {\vec {w}}=(p_{x}w_{x})|i|^{2}+(p_{y}w_{y})|j|^{2}+(p_{z}w_{z})|k|^{2}$

${\vec {p}}\cdot {\vec {w}}=(p_{x}w_{x})+(p_{y}w_{y})+(p_{z}w_{z})$

logo:

${\vec {p}}\cdot {\vec {w}}={\begin{vmatrix}1&1&1\\v_{x}&v_{y}&v_{z}\\u_{x}&u_{y}&u_{z}\end{vmatrix}}(w_{x}+w_{y}+w_{z})$

Que nos dá:

$({\vec {v}}\times {\vec {u}})\cdot {\vec {w}}={\begin{vmatrix}w_{x}&w_{y}&w_{z}\\v_{x}&v_{y}&v_{z}\\u_{x}&u_{y}&u_{z}\end{vmatrix}}$

Propriedades do produto misto

As propriedades do produto misto são análogas às dos determinantes em geral, apenas uma operação algébrica entre produtos devemos destacar:

Comutativa entre produto escalar e produto vetorial em um produto misto:

Dados três vetores: ${\vec {v}},{\vec {u}},{\vec {w}}$ em $\mathbb {R} ^{3},$ podemos comutar os vetores e produtos tais que:

${\vec {v}}\cdot ({\vec {u}}\times {\vec {w}})=({\vec {v}}\times {\vec {u}})\cdot {\vec {w}}$

No que se refere à operação em determinantes, a operação:

${\vec {v}}\cdot ({\vec {u}}\times {\vec {w}})={\begin{vmatrix}v_{x}&v_{y}&v_{z}\\u_{x}&u_{y}&u_{z}\\w_{x}&w_{y}&w_{z}\end{vmatrix}}$

enquanto que:

$({\vec {v}}\times {\vec {u}})\cdot {\vec {w}}={\begin{vmatrix}w_{x}&w_{y}&w_{z}\\v_{x}&v_{y}&v_{z}\\u_{x}&u_{y}&u_{z}\end{vmatrix}}$

Para fazer com que o primeiro determinante se torne o segundo basta permutar a mesma linha duas vezes dentro do determinante, ou seja, inverter o sinal do mesmo duas vezes, o que faz com que este retorne ao valor original. Algebricamente, os dois determinantes definem o mesmo valor quando operados. Isto define a operação como válida.

Vetores na Física

Vetores velocidade e aceleração

A trajetória de um ponto em movimento pode ser definida em cada instante t através do vetor de posição do ponto

${\vec {r}}(t)=x(t){\vec {e}}_{x}+y(t){\vec {e}}_{y}+z(t){\vec {e}}_{z}$

Cada uma das três componentes, x(t), y(t) e z(t), é uma função do tempo. Num intervalo de tempo $\Delta t=t_{2}-t_{1},$ o deslocamento do ponto é:

$\Delta {\vec {r}}={\vec {r}}_{2}-{\vec {r}}_{1}$

onde ${\vec {r}}_{1}$ e ${\vec {r}}_{2}$ são os vetores posição nos instantes $t_{1}$ e $t_{2}.$ O vetor obtido dividindo o deslocamento $\Delta {\vec {r}}$ por $\Delta t$ é o vetor velocidade média, com a mesma direção e sentido do deslocamento $\Delta {\vec {r}}.$

Trajetória de um ponto e deslocamento $\Delta {\vec {r}}$ entre dois instantes $t_{1}$ e $t_{2}.$

Define-se o vetor velocidade em cada instante, igual ao deslocamento dividido por $\Delta t,$ no limite em que $\Delta t$ se aproxima de zero:

${\vec {a}}=\lim _{\Delta \to 0}{\frac {\Delta {\vec {v}}}{\Delta t}}={\frac {d{\vec {v}}}{dt}}$

e as suas componentes serão as derivadas das componentes da velocidade:

${\vec {a}}={\overset {.}{v_{x}}}{\vec {e}}_{x}+{\overset {.}{v_{y}}}{\vec {e}}_{y}+{\overset {.}{v_{z}}}{\vec {e}}_{z}={\overset {..}{x}}{\vec {e}}_{x}+{\overset {..}{y}}{\vec {e}}_{y}+{\overset {..}{z}}{\vec {e}}_{z}$

As equações de vetor velocidade e suas componentes da velocidade são as equações de movimento em 3 dimensões, escritas de forma vetorial. Como a igualdade de dois vetores implica a igualdade das suas componentes, temos $v_{x}={\overset {.}{x}},a_{x}={\overset {.}{v_{x}}},v_{x}={\overset {..}{x}}$ e equações semelhantes para as componentes y e z. Portanto, o movimento em 3 dimensões é a sobreposição de 3 movimentos em uma dimensão, ao longo dos eixos x, y e z, e para cada um desses 3 movimentos verificam-se as equações de movimento ao longo de um eixo.

Para cada uma das componentes cartesianas existe uma equação de movimento que relaciona a aceleração com a velocidade e a posição:

$a_{x}-v_{x}{\frac {dv_{x}}{dx}}\quad a_{y}-v_{y}{\frac {dv_{y}}{dy}}\quad a_{z}-v_{z}{\frac {dv_{z}}{dz}}$

Velocidade e aceleração relativas

A figura abaixo mostra os vetores posição de um mesmo ponto P em dois referenciais diferentes. O primeiro referencial tem eixos x, y, z e origem O. Os eixos e origem do segundo referencial foram designados $x',y',z'$ e $O'.$

A relação que existe entre o vetor posição ${\vec {r}}$em relação à origem O e o vetor posição ${\vec {r}}\,'$ em relação à origem $O'$ é a seguinte:

${\vec {r}}\,'={\vec {r}}+{\vec {r}}\,'_{o}$

onde ${\vec {r}}\,'_{o}$ é o vetor de posição da primeira origem O em relação à segunda origem.

Relação entre os vetores posição de um ponto em dois referenciais diferentes

Derivando essa expressão em relação ao tempo, obtemos a relação entre as velocidades:

${\frac {d{\vec {r}}\,'}{d_{t}}}={\frac {d{\vec {r}}\,'}{d_{t}}}+{\frac {d{\vec {r}}\,'_{o}}{d_{t}}}\quad \rightarrow \quad {\vec {v}}\,'={\vec {v}}+{\vec {v}}\,'_{o}$

e derivando novamente obtemos a relação entre as acelerações:

${\frac {d{\vec {v}}\,'}{d_{t}}}={\frac {d{\vec {v}}\,'}{d_{t}}}+{\frac {d{\vec {v}}\,'_{o}}{d_{t}}}\quad \rightarrow \quad {\vec {a}}\,'={\vec {a}}+{\vec {a}}\,'_{o}$

Consequentemente, a velocidade vetorial em relação a um segundo referencial é igual à velocidade vetorial em relação ao primeiro referencial, mas a velocidade vetorial do primeiro referencial em relação ao segundo. O mesmo princípio aplica-se ao vetor aceleração. Assim, por exemplo, se nos deslocarmos com velocidade vetorial dentro de um comboio, para obtermos a nossa velocidade vetorial em relação à Terra, teríamos de somar a velocidade vetorial do comboio em relação à Terra.

A aceleração de um corpo em queda livre, em relação a um referencial que também está em queda livre, é nula.

Mas como a Terra se desloca em relação ao Sol, para encontramos a nossa velocidade em relação ao Sol teríamos de somar também a velocidade vetorial do ponto da Terra onde nos encontrarmos, em relação ao Sol. Em relação à Galaxia teríamos de somar a velocidade vetorial do Sol na galaxia, e assim sucessivamente.

O princípio de adição de acelerações vetoriais relativas é aproveitado para treinar os candidatos a astronautas. Se o astronauta, a bordo de um avião, tropeça e cai para o chão, a sua aceleração vetorial durante a queda, em relação à Terra, é o vetor ${\vec {g}}$ que aponta para o centro da Terra e tem módulo igual à aceleração da gravidade. Mas se o avião também estiver a cair livremente, a sua aceleração vetorial em relação à Terra será o mesmo vetor ${\vec {g}}.$ Portanto, a aceleração vetorial do astronauta em relação ao avião será a diferença entre essas duas acelerações em relação à Terra, que é zero. Em relação ao avião, o astronauta não acelera em nenhuma direção, mas flutua no meio do avião, durante os segundos que o piloto conseguir manter o avião em queda livre.

Produto escalar

Dois vetores ${\vec {a}}$ e ${\vec {b}}$ e o ângulo $\theta$ entre as suas direções.

O produto escalar entre dois vetores ${\vec {a}}$ e ${\vec {b}}$ e o ângulo $\theta$ formado pelas duas direções. O produto a cos $\theta$ é igual à componente do vetor ${\vec {a}}$ a direção paralela ao vetor ${\vec {b}}$ e o produto b cos $\theta$ é igual à componente do vetor b na direção paralela ao vetor a. Assim, o produto escalar é igual ao produto do módulo de um dos vetores vezes a componente do segundo vetor na direção paralela ao primeiro.

É designado de produto escalar, porque os módulos dos dois vetores e o ângulo entre as direções são grandezas escalares, que não dependem do referencial usado para os medir; consequentemente, o produto ab cos $\theta$ é também um escalar, independente do sistema de eixos usado. Duas retas que se cruzam num ponto definem dois ângulos $\theta$ e $180^{\circ }-\theta .$ No caso dos vetores, não há ambiguidade na definição do ângulo, porque se deslocarmos os vetores para um vértice comum, o ângulo será a região dos pontos que estão deslocados no sentido dos dois vetores em relação ao vértice. O produto escalar entre dois vetores com módulos a e b estará sempre dentro do intervalo [ -ab, ab]. Se o ângulo entre os vetores for agudo, cos $\theta >\theta ,$ o produto será positivo, no contrário será obtuso o produto sendo negativo. Se os vetores forem perpendiculares, o produto será nulo.

O valor mínimo do produto, - ab, obtém-se no caso em que os vetores tenham a mesma direção mas sentidos opostos. O valor máximo, ab, é obtido no caso em que os vetores tenham a mesma direção e sentido.

O produto escalar entre dois vetores é positivo se o ângulo entre os vetoresfor agudo, nulo se os vetores forem perpendiculares, ou negativo,se o ângulo for obtuso.

Como os versores têm todos módulo igual a 1, o produto entre dois versores é sempre igual ao cosseno do ângulo entre as suas direções. Assim, o ângulo entre duas direções no espaço é igual ao arco cosseno do produto escalar entre dois versores nessas direções:

$\theta _{ab}=arccos({\vec {e}}_{a}.{\vec {e}}_{b})$

No caso dos três versores cartesianos ${\vec {e}}_{x},{\vec {e}}_{y},{\vec {e}}_{z},$ o produto escalar entre dois versores diferentes é zero, por serem perpendiculares, e o produto de um dos versores consigo próprio é 1. Esse resultado pode ser usado para obter outra expressão para o cálculo do produto escalar entre dois vetores ${\vec {a}}$ e ${\vec {b}}$ Usando a propriedade distributiva do produto escalar temos:

${\vec {a}}.{\vec {b}}=(a_{x}{\vec {e}}_{x}+a_{y}{\vec {e}}_{y}+a_{z}{\vec {e}}_{z}).(b_{x}{\vec {e}}_{x}+b_{y}{\vec {e}}_{y}+b_{z}{\vec {e}}_{z})$

ou seja:

${\vec {a}}.{\vec {b}}=(a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z})$

As componentes dos dois vetores são diferentes em diferentes referenciais, mas o produto (ax bx + ay by + az bz)deverá dar o mesmo resultado em qualquer referencial, já que $({\vec {a}};{\vec {b}})$ é um escalar.

Para calcularmos o produto escalar de um vetor consigo próprio, temos que elevar ao quadrado todos seus componentes vetoriais:

${\vec {a}}.{\vec {a}}=a^{2}=a_{x}^{2}+a_{y}^{2}+a_{z}^{2}$

Assim, para calcular o módulo de um vetor com componentes (ax , ay , az ) usa-se a expressão:

$a={\sqrt {a^{2}=a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}$

Vetores deslizantes

Três forças com o mesmo módulo, direção e sentido. F1 E F2 são equivalentes,mas são diferentes de F3

Os vetores que são mais comumente estudados são denominados de vetores livres, que são considerados iguais se tiverem o mesmo módulo, direção e sentido, independentemente do ponto do espaço onde se encontrem. No caso das forças, não basta saber o módulo, direção e sentido. Se fixarmos o módulo, direção e sentido de uma força que vai ser aplicada numa porta para fechá-la, a forma como a porta será fechada dependerá também do ponto de aplicação dessa força. Quanto mais longe das dobradiças for aplicada a força, mais fácil será fechar a porta; experimente a fechar uma porta aplicando uma força a 1 cm das dobradiças!

Assim, as forças são realmente vetores deslizantes, que produzem o mesmo efeito em qualquer ponto da linha de ação (a linha reta que passa pelo ponto onde a força é aplicada, seguindo a direção da força) mas produzem efeitos diferentes quando aplicadas em diferentes linhas paralelas. No exemplo apresentado na figura , as três forças ${\vec {F}}_{1},{\vec {F}}_{2};{\vec {F}}_{3}$ têm o mesmo módulo, direção e sentido; F1 e F2 são iguais, por terem também a mesma linha de ação, mas são diferentes de F3 que atua noutra linha de ação diferente.

Adição de forças

Adição de forças com linhas de ação que se cruzam num ponto comum.

Duas forças ${\vec {F}}_{1};{\vec {F}}_{2}$ com a mesma linha de ação podem ser deslocadas para um ponto comum e somadas nesse ponto. A força resultante estará na mesma linha de ação. Se as linhas de ação das duas forças forem diferentes, mas tiverem um ponto em comum, R, como acontece com as forças na figura a seguir, podemos somá-las como se mostra no lado direito da figura: deslocam-se as duas forças para o ponto de interseção R e nesse ponto aplica-se a regra do paralelogramo; a linha de ação da força resultante será a reta que passa por esse ponto de interseção.

Quando as duas linhas de ação são paralelas, como é o caso da próxima figura, podemos usar o seguinte procedimento, ilustrado no lado direito da figura: desloca-se a força ${\vec {F}}_{2}$ na sua linha de ação $L_{2}$ com a perpendicular que passa pelo ponto P. Nos pontos P e R podemos adicionar duas forças ${\vec {F}}_{3}$ e $-{\vec {F}}_{3}$ com a mesma linha de ação, já que a soma dessas duas forças é nula.

Adição de forças paralelas.

No ponto P somamos as forças ${\vec {F}}_{1}$ e ${\vec {F}}_{3}$ sendo substituídas pela resultante ${\vec {F}}_{4}$ No ponto R somamos as forças ${\vec {F}}_{2}$ e $-{\vec {F}}_{3}$ substituindo-as pela resultante ${\vec {F}}_{5}.$ As linhas de ação das forças F4 e F5 terão sempre um ponto de interseção S, onde podemos somá-las obtendo o resultado final ${\vec {F}}_{6}$ no ponto S.

Observe na figura que, sempre que as direções e sentidos das forças forem iguais, o módulo da força resultante será igual à soma dos módulos das forças somadas $F_{6}=F_{1}+F_{2}$ Para calcular as distâncias d1 e d2, entre as linhas de ação das forças somadas e a linha de ação $L_{6}$ da força resultante, vemos na figura que h pode ser calculada nos dois triângulos:

$h=d_{1}tan\theta ={\frac {d_{1}F_{1}}{F_{3}}}\qquad \qquad \qquad h=d_{2}\;tan\beta ={\frac {d_{2}F_{2}}{F_{3}}}$

Versor - $\mathbf {u}$

Versor é um vector de valor unitário, ou seja, o módulo é igual a 1. É utilizado para indicar direcção, sentido e o ângulo formado com o eixo referencial.

${\hat {u}}={\frac {\mathbf {v} }{|\mathbf {v} |}}$

Versores podem ser utilizados como bases de um dado espaço vetorial $\mathbb {V} ^{n}.$ A condição necessária e suficiente para tanto, é que tais versores sejam linearmente independentes entre si. Uma propriedade altamente conveniente é que todo vetor pertencente ao espaço vetorial $\mathbb {V} ^{n}$ de base $(\mathbf {a_{1}} ,\mathbf {a_{2}} ,...,\mathbf {a_{n}} )$ pode ser expresso como uma combinação linear dos versores base. Assim, dado um vetor genérico $\mathbf {b} ,$ temos que $\mathbf {b} =k_{1}\mathbf {a_{1}} +k_{2}\mathbf {a_{2}} +...+k_{n}\mathbf {a_{n}} ,$ em que $k_{i}$ são números reais.

Ver também

• Versor
• Espaço vetorial
• Espaço afim, que distingue vetores e pontos
• Quadrivetor, a especialização para o espaço-tempo na teoria da relatividade
• Vetor normal
• Vetor nulo
• Vetor unitário
• Cálculo vetorial
• Fibrado vetorial
• Fasor (vetor de rotação)
• Polígono funicular

Ligações externas

• Apostila on-line da Fundação CECIERJ
• «Módulo 'vetores'». no sistema e-física do Instituto de Física da USP. 
• História dos vetores
• O que é vetor (arte vetorial)