Abstração hipostática
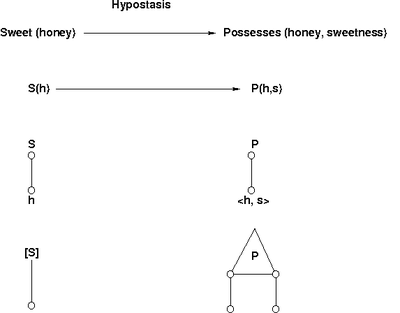
A abstração hipostática em lógica matemática, também conhecida como hipóstase ou abstração subjetiva, é um operação formal que transforma um predicado em uma relação; por exemplo, "mel é doce" é transformado em "Mel tem doçura". A relação é criada entre o assunto original e um novo termo que representa a propriedade expressa pelo predicado original.
A hipóstase muda uma fórmula proposicional da forma (X é Y) para outra da forma (X tem a propriedade de ser Y) ou (X tem Y-ismo). O funcionamento lógico do segundo objeto Y consiste apenas nos valores de verdade das proposições que têm a propriedade abstrata correspondente Y como predicado. O objeto do pensamento introduzido dessa maneira pode ser chamado de objeto hipostático e, em alguns sentidos, um objeto abstrato e um objeto formal. .
A definição acima é adaptada da que foi dada por Charles Sanders Peirce (CP 4.235, "A Matemática Mais Simples" (1902), em Collected Papers, CP 4.227-323). Como Peirce descreve, o ponto principal sobre a operação formal da abstração hipostática, na medida em que opera em expressões linguísticas formais, é que ela converte um adjetivo ou predicado em um sujeito extra, aumentando assim em um o número de intervalos "subjetivos" - chamado de aridade ou adicity - do predicado principal.
A transformação de "o mel é doce" em "mel possui doçura" pode ser vista de várias maneiras:
O traço gramatical dessa transformação hipostática é um processo que extrai o adjetivo "doce" do predicado "é doce", substituindo-o por um novo predicado de "arvoridade aumentada", e como um subproduto da reação, como foi, precipitando a substantiva "doçura" como segundo sujeito do novo predicado.
A abstração da hipóstase toma o sentido físico concreto de "gosto" encontrado em "mel é doce" e lhe dá características metafísicas formais em "mel tem doçura".
Referências
- Peirce, C. S., Coletados Papers of Charles Sanders Peirce, vols. 1-6 (1931-1935), Charles Hartshorne e Paul Weiss, eds., vols. 7-8 (1958), Arthur W. Burks, ed. Harvard University Press, Cambridge, Massachusetts.