Grupo modular

Em matemática, o grupo modular é o grupo linear especial projetivo $PSL(2, Z)$ de matrizes 2 × 2 com coeficientes inteiros e determinante um. As matrizes $A$ e $- A$ são identificadas. O grupo modular age na metade superior do plano complexo por meio de transformações fracionárias lineares, e o nome "grupo modular" vem da relação com espaços de módulos e não da aritmética modular.

Definição[editar | editar código-fonte]

O grupo modular $Γ$ é o grupo das transformações fracionárias lineares da metade superior do plano complexo, que têm a forma

z\mapsto {\frac {az+b}{cz+d}},

em que $a$ , $b$ , $c$ , $d$ são inteiros e $ad - bc = 1$ . A operação do grupo é a composição de funções.

Este grupo de transformações é isomorfo ao grupo linear especial projetivo $PSL(2, Z)$ , que é o quociente do grupo linear especial bidimensional $SL(2, Z)$ sobre os inteiros por seu centro ${I, - I}$ . Em outras palavras, $PSL(2, Z)$ consiste em todas as matrizes

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}

em que $a$ , $b$ , $c$ , $d$ são inteiros, $ad - bc = 1$ , e pares de matrizes $A$ e $- A$ são considerados idênticos. A operação do grupo é a multiplicação de matrizes usual.

Alguns autores definem o grupo modular como $PSL(2, Z)$ , e ainda outros definem o grupo modular como o grupo maior $SL(2, Z)$ .

Algumas relações matemáticas requerem a consideração do grupo $GL(2, Z)$ de matrizes com determinante mais ou menos um. ( $SL(2, Z)$ é um subgrupo deste grupo.) Da mesma forma, $PGL(2, Z)$ é o grupo quociente $GL(2, Z)/{I, - I}$ . Uma matriz 2 × 2 com determinante unitário é uma matriz simplética e, portanto, $SL(2, Z) = Sp(2, Z)$ , o grupo simplético de matrizes 2 × 2.

Obtenção dos elementos[editar | editar código-fonte]

Para encontrar elementos de $SL(2, Z)$ explicitamente, há um truque que consiste em considerar dois inteiros coprimos $a,b$ , colocá-los na matriz

{\begin{pmatrix}a&x\\b&y\end{pmatrix}}

e resolver a equação determinante

ay-bx=1

Observe que a equação do determinante força que

a,b

sejam coprimos, pois caso contrário haveria um fator

c

de tal modo que

ca'=a

,

cb'=b

, consequentemente

c(a'y-b'x)=1

não teria soluções inteiras. Por exemplo, se

a=7,{\text{ }}b=6

então a equação do determinante se torna

7y-6x=1

então tomando

y=-5

e

x=-6

obtém-se

-35-(-36)=1

, consequentemente

{\begin{pmatrix}7&-6\\6&-5\end{pmatrix}}

é uma das matrizes. Então, usando a projeção, tais matrizes definem elementos em

PSL(2, Z)

.

Propriedades da teoria dos números[editar | editar código-fonte]

O determinante unitário de

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}

implica que as frações $a b$ , $a c$ , $c d$ , $b d$ são todas irredutíveis, isto é, não têm fatores comuns (desde que os denominadores não sejam nulos, é claro). Mais geralmente, se $p q$ é uma fração na forma irredutível, então

{\frac {ap+bq}{cp+dq}}

também é irredutível (novamente, desde que o denominador seja diferente de zero). Qualquer par de frações irredutíveis pode ser conectado dessa maneira; isto é, para qualquer par de frações irredutíveis $p q$ e $r s$ , existem elementos

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \operatorname {SL} (2,\mathbf {Z} )

de tal modo que

r=ap+bq\quad {\mbox{ and }}\quad s=cp+dq.

Elementos do grupo modular fornecem uma simetria no reticulado bidimensional. Sejam $ω 1$ e $ω 2$ dois números complexos cuja razão não é real. Então o conjunto de pontos

\Lambda (\omega _{1},\omega _{2})=\{m\omega _{1}+n\omega _{2}:m,n\in \mathbf {Z} \}

é um reticulado de paralelogramos no plano. Um par diferente de vetores $α 1$ e $α 2$ irá gerar exatamente a mesma rede se, e somente se,

{\begin{pmatrix}\alpha _{1}\\\alpha _{2}\end{pmatrix}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}\omega _{1}\\\omega _{2}\end{pmatrix}}

para alguma matriz em $GL(2, Z)$ . É por esta razão que as funções duplamente periódicas, como as funções elípticas, possuem uma simetria de grupo modular.

A ação do grupo modular sobre os números racionais pode ser mais facilmente compreendida visualizando-se uma grade quadrada, com o ponto da grade $(p, q)$ correspondendo à fração $p q$ (ver pomar de Euclides). Uma fração irredutível é aquela que é visível a partir da origem; a ação do grupo modular sobre uma fração nunca leva uma visível (irredutível) a uma oculta (redutível), e vice-versa.

Observe que qualquer membro do grupo modular mapeia a reta real estendida projetivamente biunivocamente consigo mesma e, além disso, mapeia bijetivamente a reta racional estendida projetivamente (os racionais com o infinito) consigo mesma, os irracionais com os irracionais, os números transcendentes com os números transcendentais, os números não reais com os números não reais, o semiplano superior com o semiplano superior, etc.

Se $p n -1 q n -1$ e $p n q n$ são dois convergentes sucessivos de uma fração contínua, então a matriz

{\begin{pmatrix}p_{n-1}&p_{n}\\q_{n-1}&q_{n}\end{pmatrix}}

pertence a $GL(2, Z)$ . Em particular, se $bc - ad = 1$ para inteiros positivos $a$ , $b$ , $c$ , $d$ com $a < b$ e $c < d$ então $a b$ e $c d$ serão vizinhos na sequência de Farey de ordem $max(b, d)$ . Casos especiais importantes de convergentes de frações contínuas incluem os números de Fibonacci e as soluções para a equação de Pell. Em ambos os casos, os números podem ser organizados para formar um semigrupo que é subconjunto do grupo modular.

Propriedades da teoria de grupos[editar | editar código-fonte]

Apresentação[editar | editar código-fonte]

Pode-se mostrar que o grupo modular pode ser gerado pelas duas transformações

{\begin{aligned}S&:z\mapsto -{\frac {1}{z}}\\T&:z\mapsto z+1\end{aligned}}

de modo que todo elemento do grupo modular pode ser representado (de forma não única) pela composição de potências de $S$ e $T$ . Geometricamente, $S$ representa a inversão no círculo unitário seguida pela reflexão em relação ao eixo imaginário, enquanto $T$ representa uma translação de uma unidade para a direita.

Os geradores $S$ e $T$ obedecem às relações $S^{2}=1$ e $(ST) 3 = 1$ . Pode-se mostrar^[1] que estes são um conjunto completo de relações, portanto o grupo modular tem a presentação:

\Gamma \cong \left\langle S,T\mid S^{2}=I,\left(ST\right)^{3}=I\right\rangle

Esta presentação descreve o grupo modular como o grupo triangular rotacional $D(2, 3, \infty)$ (infinito, pois não há relação em $T$ ) e, portanto, pode ser mapeado sobre cada grupo triângular $(2, 3, n)$ adicionando a relação $T^{n}=1$ , que ocorre, por exemplo, no subgrupo de congruência $Γ(n)$ .

Usando os geradores $S$ e $ST$ em vez de $S$ e $T$ , mostra-se que o grupo modular é isomorfo ao produto livre dos grupos cíclicos $C 2$ e $C 3$ :

\Gamma \cong C_{2}*C_{3}

A ação de $T : z \mapsto z + 1$ sobre $H$
A ação de $S : z \mapsto - 1 z$ $S : z \mapsto - 1 z$ sobre $H$

Grupo de trança[editar | editar código-fonte]

O grupo de trança $B 3$ é a extensão central universal do grupo modular

O grupo de tranças $B 3$ é a extensão central universal do grupo modular, com estes sendo reticulados dentro do grupo de cobertura universal (topológico) $SL 2 (R) \to PSL 2 (R)$ . Além disso, o grupo modular tem um centro trivial e, portanto, o grupo modular é isomorfo ao grupo quociente de $B 3$ por seu centro; equivalentemente, ao grupo de automorfismos internos de $B 3$ .

O grupo de tranças $B 3$ por sua vez, é isomorfo ao grupo de nós do nó trifólio.

Quocientes[editar | editar código-fonte]

Os quocientes por subgrupos de congruência são de interesse significativo.

Outros quocientes importantes são os grupos triangulares $(2, 3, n)$ , que correspondem geometricamente a descer em um cilindro, quocientando a coordenada $x$ módulo $n$ , como $T^{n}=(z\mapsto z+n)$ . O grupo triangular $(2, 3, 5)$ é o grupo de simetria icosaédrica, e o grupo triangular $(2,3,7)$ (e os ladrilhos associados) é a cobertura para todas as superfícies de Hurwitz.

Apresentação como um grupo matricial[editar | editar código-fonte]

O grupo ${\text{SL}}_{2}(\mathbb {Z} )$ pode ser gerado pelas duas matrizes^[2]

$S={\begin{pmatrix}0&-1\\1&0\end{pmatrix}},{\text{ }}T={\begin{pmatrix}1&1\\0&1\end{pmatrix}}$

como

$S^{2}=-I_{2},{\text{ }}(ST)^{3}={\begin{pmatrix}0&-1\\1&1\end{pmatrix}}^{3}=-I_{2}$

A projeção ${\text{SL}}_{2}(\mathbb {Z} )\to {\text{PSL}}_{2}(\mathbb {Z} )$ transforma essas matrizes em geradores de ${\text{PSL}}_{2}(\mathbb {Z} )$ , com relações semelhantes às da presentação do grupo.

Relação com a geometria hiperbólica[editar | editar código-fonte]

O grupo modular é importante porque forma um subgrupo do grupo das isometrias do plano hiperbólico. Se considerarmos o modelo de meio plano superior $H$ da geometria plana hiperbólica, então o grupo de todas isometrias que preservam a orientação de $H$ consiste em todas as transformações de Möbius da forma

z\mapsto {\frac {az+b}{cz+d}}

em que $a$ , $b$ , $c$ , $d$ são inteiros, em vez dos números reais usuais, e $ad - bc = 1$ . Em termos de coordenadas projetivas, o grupo $PSL(2, R)$ age sobre o semiplano superior $H$ por projetividade:

[z,\ 1]{\begin{pmatrix}a&c\\b&d\end{pmatrix}}\,=\,[az+b,\ cz+d]\,\thicksim \,\left[{\frac {az+b}{cz+d}},\ 1\right].

Esta ação é fiel. Uma vez que $PSL(2, Z)$ é um subgrupo de $PSL(2, R)$ , o grupo modular é um subgrupo do grupo de isometrias que preservam a orientação de $H$ .^[3]

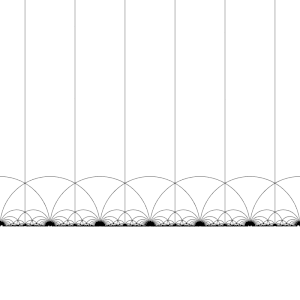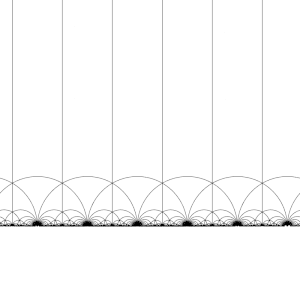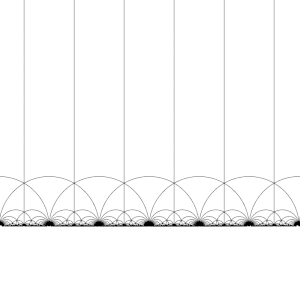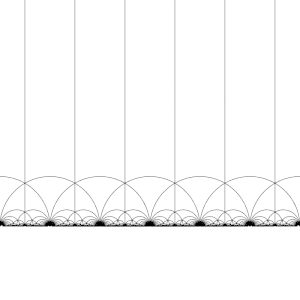
Tesselação do plano hiperbólico[editar | editar código-fonte]

Um domínio fundamental típico para a ação de $Γ$ sobre o semiplano superior

O grupo modular $Γ$ age sobre $H$ como um subgrupo discreto de $PSL(2, R)$ , ou seja, para cada $z$ em $H$ podemos encontrar uma vizinhança de $z$ que não contém nenhum outro elemento da órbita de $z$ . Isso também significa que podemos construir domínios fundamentais, que (aproximadamente) contêm exatamente um representante da órbita de cada $z$ em $H$ (É necessário cuidado com a fronteira do domínio.)

Existem muitas maneiras de construir um domínio fundamental, mas uma escolha comum é a região

R=\left\{z\in \mathbf {H} \colon \left|z\right|>1,\,\left|\,{\mbox{Re}}(z)\,\right|<{\tfrac {1}{2}}\right\}

delimitada pelas retas verticais $Re(z) = 12$ e $Re(z) = - 12$ , e a circunferência $\left|z\right|=1$ . Esta região é um triângulo hiperbólico. Ela tem vértices em $12 + i \sqrt 3 2$ e $- 12 + i \sqrt 3 2$ , onde o ângulo entre as arestas é $π 3$ , e um terceiro vértice no infinito, onde o ângulo entre suas arestas é 0.

A transformação desta região pelos elementos do grupo modular, dá origem a uma tesselação regular do plano hiperbólico por triângulos hiperbólicos congruentes conhecida como mosaico triangular de ordem infinita V6.6.∞. Observe que cada um destes triângulos tem um vértice no infinito ou no eixo real $Im(z) = 0$ . Esse mosaico pode ser estendido ao disco de Poincaré, onde cada triângulo hiperbólico tem um vértice na fronteira do disco. O mosaico do disco de Poincaré é dado de forma natural pelo $J$ -invariante, que é invariante sob o grupo modular, e atinge todos os números complexos uma vez em cada triângulo dessas regiões.

Este mosaico pode ser ligeiramente refinado, dividindo cada região em duas metades (convencionalmente coloridas em preto e branco), adicionando uma transformação que inverte a orientação; então as cores correspondem à orientação do domínio. Adicionando $(x, y) \mapsto (- x, y)$ e tomando a metade direita da região $R$ (onde $Re(z) \geq 0$ ) obtém-se a tesselação usual. Este mosaico aparece pela primeira vez publicado em (Klein 1878/79a),^[4] onde é creditado a Richard Dedekind, em referência a (Dedekind 1877).^[5]

A transformação de grupos $(2, 3, \infty) \to (2, 3, n)$ (do grupo modular para o grupo triangular) pode ser visualizada em termos desse mosaico (produzindo um mosaico na curva modular), conforme representado no vídeo à direita.

Mosaicos uniformes paracompactos da família [∞,3] [ v d e ]
Simetria: [∞,3], (*∞32)							[∞,3]⁺ (∞32)	[1⁺,∞,3] (*∞33)		[∞,3⁺] (3*∞)

		=	=	=				= or	= or	=

{∞,3}	t{∞,3}	r{∞,3}	t{3,∞}	{3,∞}	rr{∞,3}	tr{∞,3}	sr{∞,3}	h{∞,3}	h₂{∞,3}	s{3,∞}
Duais uniformes


V∞³	V3.∞.∞	V(3.∞)²	V6.6.∞	V3^∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V(3.∞)³		V3.3.3.3.3.∞

Subgrupos de congruência[editar | editar código-fonte]

Alguns subgrupos importantes do grupo modular $Γ$ , chamados subgrupos de congruência, são dados impondo relações de congruência nas matrizes associadas.

Existe um homomorfismo natural $SL(2, Z) \to SL(2, Z / N Z)$ dado pela redução das entradas módulo $N$ . Isso induz um homomorfismo no grupo modular $PSL(2, Z) \to PSL(2, Z / N Z)$ . O núcleo desse homomorfismo é chamado de subgrupo de congruência principal de nível $N$ , denotado por $Γ(N)$ . Tem-se a seguinte sequência exata curta:

1\to \Gamma (N)\to \Gamma \to {\mbox{PSL}}(2,\mathbf {Z} /N\mathbf {Z} )\to 1

.

Sendo o núcleo de um homomorfismo, $Γ(N)$ é um subgrupo normal do grupo modular $Γ$ . O grupo $Γ(N)$ é dado como o conjunto de todas as transformações modulares

z\mapsto {\frac {az+b}{cz+d}}

em que $a \equiv d \equiv \pm1 (mod N)$ e $b \equiv c \equiv 0 (mod N)$ .

É fácil mostrar que o traço de uma matriz que representa um elemento de $Γ(N)$ não pode ser -1, 0 ou 1, portanto, esses subgrupos são grupos livres de torção. (Existem outros subgrupos sem torção.)

O subgrupo principal de congruência de nível 2, $Γ(2)$ , também é chamado de grupo modular $Λ$ . Visto que $PSL(2, Z /2 Z)$ é isomorfo a $S 3$ , $Λ$ é um subgrupo do índice 6. O grupo $Λ$ consiste de todas as transformações modulares em que $a$ e $d$ são ímpares e $b$ e $c$ são pares.

Outra família importante de subgrupos de congruência é o grupo modular grupo modular $Γ 0 (N)$ definido como o conjunto de todas as transformações modulares para as quais $c \equiv 0 (mod N)$ , ou equivalentemente, como o subgrupo cujas matrizes tornam-se triangulares superiores após a redução módulo $N$ . Observe que $Γ(N)$ é um subgrupo de $Γ 0 (N)$ . As curvas modulares associadas a esses grupos são um aspecto do monstrous moonshine - para um número primo $p$ , a curva modular do normalizador é gênero zero se, e somente se, $p$ divide a ordem do grupo monstro, ou equivalentemente, se $p$ é um primo supersingular.

Monoide diádico[editar | editar código-fonte]

Um subconjunto importante do grupo modular é o monoide diádico, que é o monoide de todas as strings da forma $ST^{k}ST^{m}ST^{n}\ldots$ para inteiros positivos $k, m, n,...$ . Este monoide ocorre naturalmente no estudo das curvas fractais e descreve as simetrias de autossimilaridade da função de Cantor, da função ponto de interrogação de Minkowski e do floco de neve de Koch, cada uma sendo um caso especial da curva de de Rham geral. O monoide também tem representações lineares de dimensões superiores; por exemplo, a representação $N = 3$ pode ser entendida para descrever a autossimetria da curva de manjar branco.

Aplicações do toro[editar | editar código-fonte]

O grupo $GL(2, Z)$ consiste das transformações lineares que preservam o reticulado padrão $Z 2$ , e $SL(2, Z)$ são as transformações que preservam a orientação e que preservam este reticulado; elas, portanto, se traduzem em auto-homeomorfismos do toro (SL sendo mapeado para transformações que preservam a orientação), e de fato correspondem isomorficamente ao grupo (estendido) de classes de aplicações do toro, o que significa que todo auto-homeomorfismo do toro é isotópico a uma aplicação desta forma. As propriedades algébricas de uma matriz como elemento de $GL(2, Z)$ correspondem à dinâmica da aplicação induzida no toro.

Grupos de Hecke[editar | editar código-fonte]

O grupo modular pode ser generalizado para os grupos de Hecke, nomeados em homenagem a Erich Hecke e definido como segue.^[7]

O grupo de Hecke $H q$ com $q \geq 3$ , é o grupo discreto gerado por

{\begin{aligned}z&\mapsto -{\frac {1}{z}}\\z&\mapsto z+\lambda _{q},\end{aligned}}

em que $λ q = 2 cos π q$ . Para pequenos valores de $q \geq 3$ , tem-se:

{\begin{aligned}\lambda _{3}&=1,\\\lambda _{4}&={\sqrt {2}},\\\lambda _{5}&={\frac {1+{\sqrt {5}}}{2}},\\\lambda _{6}&={\sqrt {3}}.\end{aligned}}

O grupo modular $Γ$ é isomorfo a $H 3$ e eles têm propriedades e aplicações em comum - por exemplo, assim como tem-se o produto livre de grupos cíclicos

\Gamma \cong C_{2}*C_{3},

mais geralmente tem-se

H_{q}\cong C_{2}*C_{q},

que corresponde ao grupo triangular $(2, q, \infty)$ . Da mesma forma, há uma noção de subgrupos de congruência principais associados aos ideais principais em $Z [λ]$ .

História[editar | editar código-fonte]

O grupo modular e seus subgrupos foram estudados em detalhes pela primeira vez por Richard Dedekind e por Felix Klein como parte de seu programa Erlangen na década de 1870. No entanto, as funções elípticas intimamente relacionadas foram estudadas por Joseph Louis Lagrange em 1785, e outros resultados sobre funções elípticas foram publicados por Carl Gustav Jakob Jacobi e Niels Henrik Abel em 1827.

Ver também[editar | editar código-fonte]

Referências[editar | editar código-fonte]

↑ Alperin, Roger C. (abril de 1993). « $PSL 2 (Z) = Z 2 * Z 3$ ». Amer. Math. Monthly. 100: 385–386. JSTOR 2324963. doi:10.2307/2324963
↑ Conrad, Keith. «SL(2,Z)» (PDF)
↑ McCreary, Paul R.; Murphy, Teri Jo; Carter, Christian. «The Modular Group» (PDF). The Mathematica Journal. 9
↑ Le Bruyn, Lieven (22 de abril de 2008), Dedekind or Klein?
↑ Stillwell, John (janeiro de 2001). «Modular Miracles». The American Mathematical Monthly. 108: 70–76. ISSN 0002-9890. JSTOR 2695682. doi:10.2307/2695682
↑ Westendorp, Gerard. «Platonic tessellations of Riemann surfaces». www.xs4all.nl
↑ Rosenberger, Gerhard; Fine, Benjamin; Gaglione, Anthony M.; Spellman, Dennis. Combinatorial Group Theory, Discrete Groups, and Number Theory. [S.l.: s.n.]

[1] Alperin, Roger C. (abril de 1993). « $PSL 2 (Z) = Z 2 * Z 3$ ». Amer. Math. Monthly. 100: 385–386. JSTOR 2324963. doi:10.2307/2324963

[2] Conrad, Keith. «SL(2,Z)» (PDF)

[3] McCreary, Paul R.; Murphy, Teri Jo; Carter, Christian. «The Modular Group» (PDF). The Mathematica Journal. 9

[lebruyn-4] Le Bruyn, Lieven (22 de abril de 2008), Dedekind or Klein?

[5] Stillwell, John (janeiro de 2001). «Modular Miracles». The American Mathematical Monthly. 108: 70–76. ISSN 0002-9890. JSTOR 2695682. doi:10.2307/2695682

[westendorp-6] Westendorp, Gerard. «Platonic tessellations of Riemann surfaces». www.xs4all.nl

[7] Rosenberger, Gerhard; Fine, Benjamin; Gaglione, Anthony M.; Spellman, Dennis. Combinatorial Group Theory, Discrete Groups, and Number Theory. [S.l.: s.n.]

[1]

[2]

[3]

[4]

[5]

[6]

[7]