Imagem por ressonância magnética

A ressonância magnética (RM) é uma técnica de imagem médica usada em radiologia para formar imagens da anatomia e dos processos fisiológicos do corpo, tanto na saúde como na doença. Os scanners de RM usam campos magnéticos fortes, ondas de rádio e gradientes de campo para gerar imagens dos órgãos no corpo. A RM não envolve raios X, o que a distingue da tomografia computadorizada (TAC ou TC).
Embora os riscos dos raios X estejam agora bem controlados na maioria dos contextos médicos, a ressonância magnética ainda pode ser vista como superior à TAC a este respeito. A RM é amplamente utilizada em hospitais e clínicas para diagnóstico médico, estadiamento de doenças e acompanhamento sem expor o corpo a radiações ionizantes. Geralmente pode produzir informações de diagnóstico diferentes em comparação com a tomografia computadorizada. As varreduras de ressonância magnética geralmente levam um tempo maior, são mais altas e geralmente exigem que o sujeito entre em um tubo estreito e confinado, podendo haver riscos e desconforto associados a mesma. Além disso, as pessoas com alguns implantes médicos ou outro metal não removível dentro do corpo podem ser incapazes de se submeter a um exame de ressonância magnética de forma segura.
A RM baseia-se na ciência da ressonância magnética nuclear, tendo sido originalmente chamada de ressonância magnética nuclear (NMRI, do inglês nucelar magnetic resonance imaging)e. Certos núcleos atômicos são capazes de absorver e emitir energia de frequência de rádio quando colocados em um campo magnético externo. Na ressonância magnética clínica e de pesquisa, os átomos de hidrogênio são usados com maior frequência para gerar um sinal de radiofrequência detectável que é recebido por antenas próximas da anatomia que está sendo examinada. Os átomos de hidrogênio existem naturalmente em pessoas e outros organismos biológicos em abundância, particularmente em água e gordura. Por este motivo, a maioria das varreduras de ressonância magnética caracteriza essencialmente a localização da água e da gordura no corpo. Os pulsos das ondas de rádio estimulam a transição de energia de spin nuclear e os gradientes de campo magnético localizam o sinal no espaço. Ao variar os parâmetros da sequência de pulso, podem ser gerados diferentes contrastes entre os tecidos com base nas propriedades de relaxamento dos átomos de hidrogênio nele.
Desde o início do desenvolvimento nas décadas de 1970 e 1980, a ressonância magnética mostrou ser uma técnica de imagem altamente versátil. Enquanto ela é mais proeminente em medicina diagnóstica e pesquisa biomédica, ela também pode ser usada para formar imagens de objetos não-vivos. As varreduras de ressonância magnética são capazes de produzir uma variedade de dados químicos e físicos, além de imagens espaciais detalhadas. O aumento sustentado da demanda de ressonância magnética no setor de saúde levou a preocupações quanto à relação custo-eficácia e sobre-diagnóstico.[1][2]
Embora muitos pesquisadores já tenham descrito a maior parte da física subjacente, a imagem de ressonância magnética foi inventada por Paul C. Lauterbur em setembro de 1971. Ele publicou a teoria por trás disso em março de 1973.[3][4] No final da década de 1970, Peter Mansfield, físico e professor da Universidade de Nottingham, Inglaterra, desenvolveu a técnica de imagem de eco-planar (EPI) que levaria a varredura tomando segundos em vez de horas e produziria imagens mais claras do que Lauterbur teve.[5] Eles receberam o Prêmio Nobel de Fisiologia ou Medicina 2003 por suas "descobertas sobre ressonância magnética".
Histórico[editar | editar código-fonte]
Pioneiros da ressonância magnética nuclear[editar | editar código-fonte]


Em 1937, o físico austro-norte-americano Isidor Isaac Rabi apresentou na Physical Review 51 (p. 652) uma nova técnica para medir momentos magnéticos nucleares.
Nessa técnica, dois campos magnéticos fortes não homogêneos desviam um feixe molecular em sentidos opostos, produzindo um efeito de focalização.[6]
Por outro lado, no meio da trajetória do feixe, um campo magnético forte homogêneo produz uma frequência de Larmor nos núcleos das moléculas do feixe, no mesmo instante em que um campo magnético alternado fraco é aplicado ao feixe.
Assim, se esse campo estiver em ressonância com a frequência da precessão larmoriana, o núcleo ressonante é lançado fora de sua trajetória normal. Essa técnica de Rabi ficou conhecida como Ressonância Magnética Nuclear.
Rabi e seus colaboradores, os físicos Zacharias, S. Millman e Polykarp Kusch realizaram experiências nas quais mediram o momento magnético do lítio (Li) , e que foram relatadas, em 1938, na Physical Review 53 (p. 318) divulgando um artigo que mostrou sem dúvida a primeira observação de RMN.[6]
Em 1944, o Prêmio Nobel de Física foi concedido para Rabi por seus trabalhos pioneiros sobre Ressonância Magnética Nuclear. Estimulado pelos físicos alemães Otto Stern e Immanuel Estermann, em 1933 na qual foi medido o momento magnético do próton.
Em 1939, Felix Bloch e o físico norte americano Luis Walter Alvarez mediram o momento magnético do nêutron, usando uma adaptação da técnica de Rabi (1937) a um intenso feixe de nêutrons oriundos de um cíclotron. O desvio magnético da técnica de Rabi foi substituído por um efeito de polarização desse feixe.
Em 1942, Cornelis Jacobus Gorte e L. F. J. Broer publicaram na Physica 9 o resultado de uma experiência na qual tentaram, sem sucesso, medir ressonâncias nucleares.
Em 1945, o físico russo E. Zavoisky apresentou no Fiziologiocheskii Zhurnal 9 o resultado de experiências, nas quais observou a ressonância magnética nuclear ao aplicar um campo magnético uniforme a sais (cobre e manganês) contendo íons divalentes.
Em 1946, os físicos norte-americanos Edward Mills Purcell, Henry Cutler Torreye R. V. Pound e, independentemente, Félix Bloch , W. W. Hansen e M. Packard publicaram artigos, respectivamente, na Physical Review 69, nos quais anunciaram que haviam descoberto efeitos de ressonância magnética nuclear em sólidos e líquidos.
Na experiência realizada por Purcell, Torry e Pound o método utilizado foi o de obter a subtração de energia a um campo magnético oscilante por núcleos sujeitos a um campo magnético forte e fixo, método esse capaz de medir a frequência de Larmor, que é importante para a determinação do momento magnético dos núcleos.
O material por eles utilizado foi a parafina, a qual contém muitos prótons, que neste caso há dois níveis de separação da frequência v. Por sua vez, Bloch, Hansen e Packard utilizaram um método semelhante descrito acima; porém, eles detectaram a ressonância magnética nuclear pela intensidade máxima de sinais induzidos em uma bobina detectora perpendicular quer ao campo magnético fixo, quer ao campo magnético oscilante.
Em 1947, os físicos norte-americanos John Elliot Nafe e Edward B. Nelson, e o austro-norte-americano Isidor Isaac Rabi publicaram um artigo na Physical Review 71, no qual apresentaram o resultado de uma experiência que indicava ser o momento magnético do elétron (µe) um pouco maior do que o magnetão de Bohr (µ0). Resultado análogo a esse foi apresentado por D. E. Nagel, R. S. Julian e J. R. Zacharias na Physical Review 72, ambos eram trabalhos que falavam sobre estruturas hiperfinas.
Em 2019, pesquisadores realizaram a menor imagem por ressonância magnética do mundo para capturar os campos magnéticos de átomos individuais.[7]
Construção e física[editar | editar código-fonte]
Para realizar um estudo, a pessoa fica posicionada dentro de um scanner de MRI que forma um forte campo magnético em torno da área a ser imageada. Na maioria das aplicações médicas, os prótons (núcleos de hidrogênio) em tecidos contendo moléculas de água criam um sinal que é processado para formar uma imagem do corpo. Primeiro, a energia de um campo magnético oscilante temporariamente é aplicada ao paciente na frequência de ressonância apropriada. Os átomos de hidrogênio excitados emitem um sinal de radiofrequência, que é medido por uma bobina receptora. O sinal de rádio pode ser feito para codificar informações de posição, variando o campo magnético principal usando bobinas de gradiente. À medida que estas bobinas são rapidamente ligadas e desligadas, elas criam o ruído repetitivo característico de uma varredura de ressonância magnética. O contraste entre diferentes tecidos é determinado pela taxa em que os átomos excitados retornam ao estado de equilíbrio. Os agentes de contraste exógenos podem ser administrados por via intravenosa, oral ou intra-articular.[8]
Os principais componentes de um scanner de ressonância magnética são: o ímã principal, que polariza a amostra, as bobinas de compensação para corrigir as não-homogeneidades no campo magnético principal, o sistema de gradiente que é usado para localizar o sinal de MR e o sistema de RF, o que excita a amostra e detecta o sinal de RMN resultante. Todo o sistema é controlado por um ou mais computadores.
A RM requer um campo magnético que seja forte e uniforme. A força de campo do ímã é medida em teslas e enquanto a maioria dos sistemas operam a 1,5 T, sistemas comerciais estão disponíveis entre 0,2 e 7 T. A maioria dos ímãs clínicos são ímãs supercondutores, que requerem hélio líquido. As intensidades de campo mais baixas podem ser alcançadas com ímãs permanentes, que são frequentemente usados em scanners de MRI "abertos" para pacientes claustrofóbicos.[9] Recentemente, a MRI foi demonstrada também em campos ultra baixos, ou seja, na faixa microtesla-a-militesla, onde a qualidade de sinal suficiente é possível por pré-polarização (na ordem de 10 a 100 mT) e medindo os campos de precessão de Larmor em cerca de 100 µT com dispositivos de interferência quântica supercondutores altamente sensíveis (SQUIDs).[10][11][12]
T1 e T2[editar | editar código-fonte]
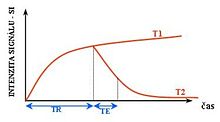
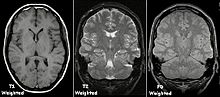
Cada tecido retorna ao seu estado de equilíbrio após a excitação pelos processos independentes de T1 (spin-tretice) e T2 (spin-spin) de relaxamento. Para criar uma imagem ponderada em T1, a magnetização pode ser recuperada antes de medir o sinal MR, alterando o tempo de repetição (TR). Esta ponderação de imagem é útil para avaliar o córtex cerebral, identificando tecido adiposo, caracterizando lesões focais e, em geral, para obter informações morfológicas, bem como para imagens pós-contraste. Para criar uma imagem ponderada em T2, a magnetização pode decair antes de medir o sinal MR alterando o tempo de eco (TE). Esta ponderação de imagem é útil para detectar edema e inflamação, revelando lesões de substância branca e avaliando a anatomia zonal na próstata e no útero.
A exibição padrão de imagens de MRI é representar características de fluido em imagens em preto e branco, onde diferentes tecidos são os seguintes:
| Sinal | T1-ponderado | T2-ponderado |
|---|---|---|
| Alto |
| |
| Intermediário | Matéria cinzenta mais escura que matéria branca | Matéria branca mais escura do que a matéria cinzenta |
| Baixo |
Agentes de contraste[editar | editar código-fonte]
A ressonância magnética para imagens de estruturas anatômicas ou fluxo sanguíneo não requer agentes de contraste, pois as propriedades variáveis dos tecidos ou sangue proporcionam contrastes naturais. No entanto, para tipos de imagem mais específicos, os agentes de contraste intravenosos mais utilizados são baseados em quelatos de gadolínio.[15] Em geral, esses agentes se mostraram mais seguros do que os agentes de contraste iodados utilizados na radiografia ou TAC. As reações anafilactóides são raras, ocorrendo em cerca de 0,03 a 0,1%.[16] De particular interesse é a menor incidência de nefrotoxicidade, em comparação com os agentes iodados, quando administrados em doses usuais. Isto fez uma varredura de ressonância magnética contrastante uma opção para pacientes com insuficiência renal, que de outra forma não seriam capazes de ser submetidos a TAC com contraste.[17]
Embora os agentes de gadolínio se tenham revelado úteis para pacientes com insuficiência renal, em pacientes com insuficiência renal grave que requer diálise, existe o risco de uma doença rara mas grave, fibrose sistêmica nefrogênica, que pode estar ligada ao uso de certos agentes contendo gadolínio. O mais frequentemente ligado é a gadodiamida, mas outros agentes também foram ligados.[18] Embora uma ligação causal não tenha sido definitivamente estabelecida, as diretrizes atuais nos Estados Unidos são que os pacientes em diálise só devem receber agentes de gadolínio quando essenciais e que a diálise deve ser realizada o mais rápido possível após a varredura para remover o agente do corpo prontamente.[19][20] Na Europa, onde mais agentes contendo gadolínio estão disponíveis, uma classificação dos agentes de acordo com os riscos potenciais foi liberada.[21][22] Recentemente, foi aprovado um novo agente de contraste chamado gadoxetate, Eovist de marca (US) ou Primovist (EU), para uso diagnóstico: isso tem o benefício teórico de um caminho de excreção dupla.[23]
RM por órgão ou sistema[editar | editar código-fonte]

A RM possui uma ampla gama de aplicações no diagnóstico médico e estima-se que mais de 25 mil scanners estejam em uso em todo o mundo.[24] A RM afeta o diagnóstico e o tratamento em muitas especialidades, embora o efeito sobre os melhores resultados de saúde seja incerto.[25]
A ressonância magnética é a investigação de escolha no estadiamento pré-operatório do câncer retal e da próstata e, tem um papel no diagnóstico, estadiamento e acompanhamento de outros tumores.[26]
Neuroimagem[editar | editar código-fonte]

A ressonância magnética é a ferramenta investigativa de escolha para cânceres neurológicos, pois tem melhor resolução do que a TC e oferece uma melhor visualização da fossa posterior. O contraste fornecido entre matéria cinza e branca torna a ressonância magnética melhor opção para muitas condições do sistema nervoso central, incluindo doenças desmielinizantes, demência, doença cerebrovascular, doenças infecciosas e epilepsia.[27] Uma vez que muitas imagens são retiradas em milisegundos, mostra como o cérebro responde a diferentes estímulos, permitindo que os pesquisadores estudem as anormalidades cerebrais funcionais e estruturais em distúrbios psicológicos.[28] A RM também é utilizada na cirurgia estereotáxica guiada por MRI e radiocirurgia para o tratamento de tumores intracranianos, malformações arteriovenosas e outras condições tratáveis cirurgicamente usando um dispositivo conhecido como N-localizer.[29][30][31][32][33][34][35][36][37][38][39][40][41][42]
Cardiovascular[editar | editar código-fonte]
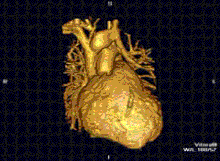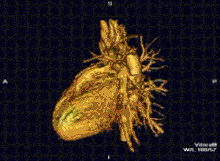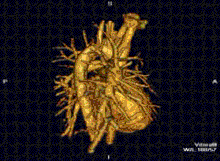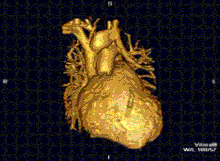
A RM cardíaca é complementar a outras técnicas de imagem, como ecocardiografia, TC cardíaca e medicina nuclear. As suas aplicações incluem avaliação da isquemia miocárdica e viabilidade, cardiomiopatias, miocardite, sobrecarga de ferro, doenças vasculares e cardiopatia congênita.[43]
Musculoesquelético[editar | editar código-fonte]
As aplicações no sistema músculo-esquelético incluem imagens espinhais, avaliação de doenças das articulações e tumores de tecidos moles.[44]
Fígado e gastrointestinal[editar | editar código-fonte]
O MR hepatobiliar é usado para detectar e caracterizar lesões do fígado, pâncreas e ductos biliares. Os distúrbios focais ou difusos do fígado podem ser avaliados utilizando imagens de fase em oposição ponderada em fase oposta e de contraste dinâmico. Os agentes de contraste extracelular são amplamente utilizados na ressonância magnética do fígado e os novos agentes de contraste hepatobiliares também proporcionam a oportunidade de realizar imagens biliares funcionais. A imagem anatômica dos canais biliares é conseguida usando uma sequência fortemente ponderada em T2 na colangiopancreatografia por ressonância magnética (MRCP). A imagem funcional do pâncreas é realizada após administração de secretina. A enterografia MR fornece avaliação não-invasiva da doença inflamatória do intestino e dos tumores do intestino delgado. A colonografia de MR pode desempenhar um papel na detecção de pólipos grandes em pacientes com risco aumentado de câncer colorretal.[45][46][47][48]
Angiografia[editar | editar código-fonte]
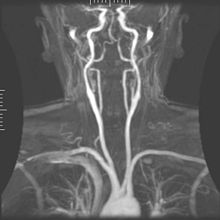
A angiografia por ressonância magnética (MRA) gera imagens das artérias para avaliá-las para estenose (estreitamento anormal) ou aneurismas (dilatação da parede vascular, em risco de ruptura). O MRA é frequentemente usado para avaliar as artérias do pescoço e do cérebro, a aorta torácica e abdominal, as artérias renais e as pernas (chamado de "escorrer"). Uma variedade de técnicas podem ser usadas para gerar as imagens, como a administração de um agente de contraste paramagnético (gadolínio) ou usando uma técnica conhecida como "aprimoramento relacionado ao fluxo" (por exemplo, sequências de tempo de voo 2D e 3D), onde a maior parte do sinal em uma imagem é devido ao sangue que recentemente se mudou para esse plano. As técnicas que envolvem acumulação de fase (conhecida como angiografia por contraste de fase) também podem ser usadas para gerar mapas de velocidade de fluxo com facilidade e precisão. A venografia por ressonância magnética (MRV) é um procedimento similar que é usado para imagens de veias. Neste método, o tecido agora está excitado inferiormente, enquanto o sinal é recolhido no plano imediatamente superior ao plano de excitação - criando assim o sangue venoso que recentemente se moveu do plano excitado.[49]
Princípios básicos de ressonância magnética nuclear[editar | editar código-fonte]
A ressonância magnética nuclear como todas as formas de espectroscopia, trata-se da interação da radiação eletromagnética com a matéria.[6] Entretanto, RMN diferencia-se da espectroscopia óptica em vários aspectos fundamentais, tais como:
primeiro, a separação entre os níveis de energia é um resultado da interação do momento magnético de um núcleo atômico com um campo magnético aplicado; segundo, a interação é com a componente magnética da radiação eletromagnética em vez da componente elétrica.
Sendo que o efeito de RMN ocorre para núcleos que possuem momentos magnéticos e angulares e , respectivamente.
Os núcleos apresentam momentos magnéticos e angulares paralelos entre si, respeitando a expressão onde o fator giromagnético.
O momento angular é definido, quanticamente, por
onde um operador adimensional, também denominado de momento angular ou spin, cujos valores podem ser somente números inteiros ou semi-inteiros 0, 1/2, 1, 3/2, 2(...).
A separação entre os níveis de energia é um resultado da interação do momento magnético do núcleo atômico com o campo magnético aplicado.
Na espectroscopia de RMN é possível controlar a radiação eletromagnética (faixa de radiofrequência ou RF) e descrever a interação desta radiação com os spins nucleares do sistema. Isto contribui em grande parte para o desenvolvimento do grande número de técnicas utilizadas em RMN. Quase todos os elementos químicos têm ao menos um isótopo com um núcleo atômico que possui momento magnético, e quando este é colocado em um campo magnético externo, e a ele for aplicada uma excitação com frequência igual a sua frequência de precessão , tal núcleo é retirado de seu estado de equilíbrio. Após a retirada do campo de RF, este núcleo tende a voltar ao seu estado fundamental de equilíbrio através dos processos de relaxação spin-rede (T1) e relaxação spin-spin (T2)
Ressonância magnética nuclear do estado sólido[editar | editar código-fonte]

A interação de um spin nuclear com um campo magnético resulta em 2I + 1 níveis de energia com espaçamentos iguais de unidade .[6]
Entretanto, várias interações podem deslocar a frequência da transição ou desdobrar uma transição em vários picos.
Em consequência da complexidade de suas estruturas moleculares ou por causa da pequena diferença entre unidades isoméricas, a investigação da moléculas e macromoléculas no estado sólido requer boa resolução espectral.
Os deslocamentos químicos no espectro de RMN são muito sensíveis à estrutura e conformação da molécula, às interações intermoleculares, à troca química, mudanças de conformação e os tempos de relaxação são sensíveis à dinâmica molecular.
Por estes motivos, ressonância magnética nuclear do estado sólido é uma espectroscopia muito útil ao estudo de polímeros.
Interações de RMN do estado sólido[editar | editar código-fonte]
Experimentos de RMN com amostras no estado sólido apresentam resultados diretamente relacionados com as propriedades físicas dos sistemas estudados. A representação da energia dos spins nucleares em experimentos de ressonância magnética nuclear é expressa pelo operador Hamiltoniano. Assim, o Hamiltoniano de spin nuclear que descreve as interações que definem a posição e a forma da linha espectral pode ser decomposta em uma soma de várias interações e assume a seguinte forma:
Sendo Hz e HRF as interações Zeeman e de radiofrequência respectivamente, consideradas interações externas. pois são definidas pelos campos magnéticos estático, gerado pelo magneto supercondutor, e de RF, gerado pelas bobinas onde é inserida a amostra. As interações externas associadas ao acoplamento do momento magnético de spin com o campo magnético estático (efeito Zeeman) e com a oscilação da radiofrequência aplicada perpendicularmente ao campo magnético estático , causa transições entre os níveis adjacentes. As demais interações são consideradas internas, visto que elas estão intrinsecamente associadas às características microscópicas da amostra, as quais alteram a distribuição dos níveis de energia definidos pela interação Zeeman, modificando o espectro.
Interação Zeeman[editar | editar código-fonte]
O Hamiltoniano Zeeman, representa o acoplamento do momento magnético nuclear com o campo magnético externo estático , dada por:

sendo esta a equação fundamental de RMN, uma vez que sem o efeito Zeeman não pode haver espectroscopia de RMN.[6]
Representando o efeito Zeeman classicamente por:
Demonstrando o operador Hamiltoniano a partir do valor acima, temos:
Dependendo do valor de mI , designado por número quântico magnético, tem-se:
e a diferença de energia entre os dois estados é , onde Eα e Eβ são os valores próprios do operador HZ, na equação de onda de RMN para esta interação. A equação secular para esta interação fica da seguinte forma:
sendo que ∆E=hv ,e igualando esta quantidade com , temos
Na realidade, quando uma amostra é colocada na presença de um campo magnético , há na ordem de 1023 núcleos atômicos pressionando em torno dele. Para os núcleos com m=1/2, possuem menor energia e pressionam em torno do campo magnético externo orientados a favor do campo, e outros núcleos com m=-1/2, possuem maior energia e pressionam na direção oposta ao campo magnético externo, sendo estas distribuições e , respectivamente.[6]
A partir da Mecânica estatística tem-se que a razão entre estas distribuições de energia é dada pela distribuição de Boltzmann:
Tomando a intensidade do campo magnético da ordem de 1 Tesla, a temperatura da amostra em torno da temperatura ambiente, T ≈ 300K, e o fator giromagnético do núcleo do átomo de hidrogênio, , da expressão acima obtém-se que para temperatura ambiente.
Como , consequentemente determina-se que a diferença de distribuição é de ∆N=2,11×1018 spins, implicando no fato de que N+ =3,0099894×1023 spins pressionam no sentido oposto ao campo magnético externo e N-= 3,01001106×1023 spins pressionam em torno do campo. Desta forma, ∆N/N=3,5×10−6, ou seja, a diferença de população entre os dois níveis é da ordem de partes por milhão (ppm) com relação ao número total de spins da amostra. Devido à precessão aleatória dos spins em torno da direção z, a magnetização transversal ao campo é nula, e a magnetização longitudinal, ao longo da direção do campo magnético aplicado, é dada por . Logo , é a magnetização resultante que surge na amostra quando a mesma é colocada sob a ação de um campo magnético, a qual é normalmente denominada por magnetização de equilíbrio.[6]
Interação dos sistemas de spin e RF[editar | editar código-fonte]
Transições entre níveis de energias de um sistema de spins podem ser realizadas excitando os núcleos de um dado sistema por meio da aplicação de um campo magnético oscilante com frequência adequada (faixa de MHz ou r.f.) para promover transições de spins entre os níveis de energia Zeeman. Sendo ω1 frequência de oscilação do campo , temos que HRF é dado por:
O efeito de HRF é induzir transições entre os auto-estados de α→β , com probabilidades por unidade de tempo dada pela regra de ouro de Fermi:
A expressão da probabilidade é tanto maior quanto maiores forem o fator giromagnético do núcleo em questão e a intensidade do campo de r.f. de excitação; a função δ, centrada na frequência de Larmor, garante que o campo deve oscilar com frequência exatamente igual ao espaçamento, em frequência dos níveis zeeman, para que ocorra a absorção de energia pelo sistema de spins.
Interação dipolar[editar | editar código-fonte]
O acoplamento entre os spins nucleares através dos seus momentos dipolares magnéticos, é representado pelo hamiltoniano dipolar que é expresso pela seguinte equação[6] :
onde é o tensor de segunda ordem, simétrico e de traço nulo, que representa a interação dipolar magnética. Classicamente um dipólo magnético µ1 produz um campo magnético a uma distância r dado por:
(B)
Este é o campo produzido por um dipólo µI e a energia de interação com outro dipólo µS a um ponto onde o campo magnético é dado por BI é
(A)
Substituindo (A) em (B), temos

o análogo quântico é
onde
Interação quadrupolar[editar | editar código-fonte]
As interações quadrupolares estão presentes somente quando núcleos com spinI > ½ estão envolvidos. Tais núcleos possuem uma distribuição assimétrica de cargas elétricas e interagem com os gradientes de campo elétrico presente na amostra.
A interação elétrica entre este quadrupolo e o ambiente eletrônico encurta o tempo de vida dos estados magnéticos (α e β) de spin nuclear, resultando também no alargamento da linha de ressonância.
Sendo esta interação importante se o núcleo tiver spin I >1/2, com um momento quadrupolar eQ. Neste caso o Hamiltoniano para um só spin I quadrupolar será:
Onde é o tensor quadrupolar, e é o tensor gradiente do campo elétrico no local do núcleo.
RMN e a dinâmica do movimento molecular[editar | editar código-fonte]

A dinâmica molecular apresenta importantes efeitos nas propriedades mecânicas e físico-químicas de moléculas, tais como no comportamento de materiais amorfos, condução em polímeros, na contribuição da classificação de alimentos naturais, na classificação de resinas, na caracterização de amidos, etc. Os processos de relaxação da magnetização são causados devido ao movimento molecular, e as taxas de relaxação medidas podem ser relacionadas com o tempo τc .
A medida da taxa de relaxação provê informações sobre a dinâmica molecular em vários regimes de frequência, onde pode-se medir os tempos de relaxação T1,T2 e T1ρ, e com isso, consegue-se estudar diferentes movimentos que ocorrem com uma distribuição de frequências.
Em RMN podemos classificar o estudo da dinâmica do estado sólido em três etapas: rápida, de correlação característico do movimento, intermediária e lenta. Movimentos rápidos, com frequências da ordem de MHz, podem ser detectados por meio de experimentos de relaxação spin-rede (T1).[6]
A dinâmica intermediária, com taxas entre 10–100 kHz, pode ser caracterizada por experimentos de análise de largura de linha e técnicas de relaxação como T1ρ (relaxação spin-rede no referencial rotante).
Sistemas que envolvem processos dinâmicos lentos (0.1 – 1000 Hz), as informações podem ser obtidas através de experimentos de RMN de Exchange, onde os movimentos moleculares lentos são observados em termos de mudanças na frequência de RMN, a qual reflete diretamente mudanças na orientação dos segmentos moleculares. Na figura é esboçado os parâmetros de relaxação e seu regime de frequências.
Espectroscopia de ressonância magnética nuclear[editar | editar código-fonte]
Em espectroscopia, o processo de ressonância magnética é similar aos demais. Pois também ocorre a absorção ressonante de energia eletromagnética, ocasionada pela transição entre níveis de energia rotacionais dos núcleos atômicos, níveis estes desdobrados em função do campo magnético através do efeito Zeeman anômalo.
Como o campo magnético efetivo sentido pelo núcleo é levemente afetado (perturbação essa geralmente medida em escala de partes por milhão) pelos débeis campos eletromagnéticos gerados pelos elétrons envolvidos nas ligações químicas (o chamado ambiente químico nas vizinhanças do núcleo em questão), cada núcleo responde diferentemente de acordo com sua localização no objeto em estudo, atuando assim como uma sonda sensível à estrutura onde se situa.
Magnetismo macroscópico e microscópico[editar | editar código-fonte]
O efeito da ressonância magnética nuclear fundamenta-se basicamente na absorção ressonante de energia eletromagnética na faixa de frequências das ondas de rádio. Mais especificamente nas faixas de VHF.
Mas a condição primeira para absorção de energia por esse efeito é de que os núcleos em questão tenham momento angular diferente de zero.
Núcleos com momento angular igual a zero não tem momento magnético, o que é condição indispensável a apresentarem absorção de energia eletromagnética. Razão, aliás, pertinente a toda espectroscopia.
A energia eletromagnética só pode ser absorvida se um ou mais momentos de multipolo do sistema passível de absorvê-la são não nulos, além do momento de ordem zero para eletricidade (equivalente à carga total).
Para a maior parte das espectroscopias, a contribuição mais importante é aquela do momento de dipolo. Se esta contribuição variar com o tempo, devido a algum movimento ou fenômeno periódico do sistema (vibração, rotação, etc), a absorção de energia da onda eletromagnética de mesma frequência (ou com frequências múltiplas inteiras) pode acontecer.
Um campo magnético macroscópico é denotado pela grandeza vetorial conhecida como indução magnética B. Esta é a grandeza observável nas escalas usuais de experiências, e no sistema SI é medida em Tesla, que é equivalente a Weber/m3.
Em nível microscópico, temos outra grandeza relacionada, o campo magnético H, que é o campo que se observa a nível microscópico. No sistema SI é medido em Ampere/m.
O vetor dipolo magnético μ é um dos momentos de multipolo magnéticos e é dado matematicamente por
onde
- M é o polo magnético
- l é o vetor distância entre os polos do sentido S → N
Para os trabalhos práticos, lida-se com o vetor magnetização M que é um vetor representativo de todos os vetores μ sobre um volume V:
M é, portanto, uma grandeza intensiva.
No vácuo, existe uma relação matemática entre o vetor B e o vetor H:
onde é a permeabilidade magnética no vácuo.
Para meios materiais, a relação válida é a seguinte:
Outras configurações especializadas[editar | editar código-fonte]
Espectroscopia de ressonância magnética
A espectroscopia de ressonância magnética (MRS) é usada para medir os níveis de metabólitos diferentes nos tecidos corporais. O sinal MR produz um espectro de ressonâncias que corresponde a diferentes arranjos moleculares do isótopo sendo "excitados". Essa assinatura é usada para diagnosticar certos distúrbios metabólicos, especialmente aqueles que afetam o cérebro[50] e para fornecer informações sobre o metabolismo tumoral.[51]
A imagem espectroscópica de ressonância magnética (MRSI) combina métodos espectroscópicos e de imagem para produzir espectros espacialmente localizados dentro da amostra ou do paciente. A resolução espacial é muito menor (limitada pelo SNR disponível), mas os espectros em cada voxel contém informações sobre muitos metabólitos. Como o sinal disponível é usado para codificar informações espaciais e espectrais, a MRSI requer alta SNR somente possível em maiores intensidades de campo (3 T e acima).
MRI em tempo real[editar | editar código-fonte]
A RM em tempo real refere-se ao monitoramento contínuo ("filmagem") de objetos em movimento em tempo real. Embora muitas estratégias diferentes tenham sido desenvolvidas desde o início dos anos 2000, um desenvolvimento recente relatou uma técnica de ressonância magnética em tempo real baseada em FLASH radial e reconstrução iterativa que produz uma resolução temporal de 20 a 30 milissegundos para imagens com uma resolução no plano de 1,5 a 2,0 mm. O novo método promete adicionar informações importantes sobre doenças das articulações e do coração. Em muitos casos, os exames de ressonância magnética podem tornar-se mais fáceis e mais confortáveis para os pacientes.[52]
MRI intervencionista[editar | editar código-fonte]
A falta de efeitos nocivos para o paciente e o operador tornam a MRI adequada para a radiologia de intervenção, onde as imagens produzidas por um scanner de ressonância magnética orientam procedimentos minimamente invasivos. Tais procedimentos devem ser feitos sem instrumentos ferromagnéticos.
Um subconjunto crescente especializado de ressonância magnética intervencionista é a ressonância magnética intra-operatória, na qual os médicos utilizam uma RM em cirurgia. Alguns sistemas de ressonância magnética especializados permitem a imagem simultânea com o procedimento cirúrgico. Mais típico, no entanto, é que o procedimento cirúrgico é temporariamente interrompido para que a ressonância magnética possa verificar o sucesso do procedimento ou orientar o trabalho cirúrgico subsequente.
Ultra-sonografia focada guiada por ressonância magnética
Na terapia MRgFUS, os feixes de ultra-som são focados em uma imagem térmica controlada por tecido e devido à deposição significativa de energia no foco, a temperatura dentro do tecido aumenta para mais de 65 °C (150 °F), destruindo completamente isto. Esta tecnologia pode atingir a ablação precisa de tecido doente. A imagem da RM fornece uma visão tridimensional do tecido alvo, permitindo uma focagem precisa da energia ultra-sonográfica. A imagem de MR fornece imagens quantitativas, em tempo real, térmicas da área tratada. Isso permite que o médico assegure-se de que a temperatura gerada durante cada ciclo de energia ultra-sonográfica seja suficiente para causar ablação térmica dentro do tecido desejado e, se não, para adaptar os parâmetros para garantir um tratamento eficaz.[53]
Imagem multinucleada
O hidrogênio é o átomo de núcleo com imagem mais frequente na ressonância magnética porque está presente em tecidos biológicos em grande abundância, e porque sua alta relação giromagnética dá um sinal forte. No entanto, qualquer núcleo com uma rotação nuclear líquida poderia ser imaginado com ressonância magnética. Tais núcleos incluem hélio-3, lítio-7, carbono-13, flúor-19, oxigênio-17, sódio-23, fósforo-31 e xenon-129. 23Na e 31P são naturalmente abundantes no corpo, então podem ser imaginadas diretamente. Os isótopos gasosos, como o 3He ou 129Xe, devem ser hiperpolarizados e, em seguida, inalados, uma vez que a sua densidade nuclear é muito baixa para produzir um sinal útil em condições normais. 17O e 19F podem ser administrados em quantidades suficientes em forma líquida (por exemplo, 17O-água) que a hiperpolarização não é uma necessidade. O uso de hélio ou xenônio tem a vantagem de reduzir o ruído de fundo e, portanto, aumentar o contraste para a própria imagem, porque esses elementos não estão normalmente presentes em tecidos biológicos.[54]
Além disso, o núcleo de qualquer átomo que tem uma rotação nuclear líquida e que está ligado a um átomo de hidrogênio pode ser potencialmente fotografado através de transferência de magnetização heteronuclear MRI que iria imaginar o núcleo de hidrogênio de alta relação giromagnética em vez do núcleo de baixa razão giromagnética que está ligado ao átomo de hidrogênio.[55] Em princípio, a transferência de magnetização heteronuclear pode ser utilizada para detectar a presença ou ausência de ligações químicas específicas.[56]
A imagem multinuclear é principalmente uma técnica de pesquisa no presente. No entanto, as aplicações potenciais incluem imagens funcionais e imagens de órgãos mal vistos em 1H RM (por exemplo, pulmões e ossos) ou como agentes de contraste alternativos. Inalação hiperpolarizada 3He pode ser usada para imagem da distribuição de espaços de ar dentro dos pulmões. Soluções injetáveis contendo 13C ou bolhas estabilizadas de 129Xe hiperpolarizado foram estudadas como agentes de contraste para angiografia e imagem de perfusão. 31P pode potencialmente fornecer informações sobre densidade e estrutura óssea, bem como imagens funcionais do cérebro. A imagem multinucleada tem o potencial de traçar a distribuição do lítio no cérebro humano, este elemento que encontra o uso como um medicamento importante para aqueles com condições como o transtorno bipolar.
Imagem molecular por ressonância magnética
A ressonância magnética tem as vantagens de ter uma resolução espacial muito alta e é muito experiente em imagens morfológicas e imagens funcionais. A MRI tem várias desvantagens. Primeiro, a RM tem uma sensibilidade de cerca de 10−3 mol/L a 10−5 mol/L, o que, em comparação com outros tipos de imagem, pode ser muito limitante. Este problema decorre do fato de que a diferença de população entre os estados de rotação nuclear é muito pequena à temperatura ambiente. Por exemplo, em 1,5 teslas, uma força de campo típica para a ressonância magnética clínica, a diferença entre estados de energia alta e baixa é de aproximadamente 9 moléculas por 2 milhões. As melhorias para aumentar a sensibilidade à RM incluem aumento da força do campo magnético e hiperpolarização através de bombeamento óptico ou polarização nuclear dinâmica. Há também uma variedade de esquemas de amplificação de sinal baseados na troca química que aumentam a sensibilidade.
Para obter imagens moleculares de biomarcadores de doenças usando MRI, são necessários agentes de contraste de MRI direcionados com alta especificidade e alta relaxividade (sensibilidade). Até a data, muitos estudos foram dedicados ao desenvolvimento de agentes de contraste de MRI-alvo para obter imagens moleculares por ressonância magnética. Comumente, foram aplicados peptídeos, anticorpos ou ligandos pequenos, e domínios de pequenas proteínas, tais como os afibodies HER-2, para atingir a segmentação. Para melhorar a sensibilidade dos agentes de contraste, essas porções de segmentação geralmente estão ligadas a agentes de contraste de MRI de alta carga ou agentes de contraste de MRI com altas relaxividades.[57] Uma nova classe de genes que visam agentes de contraste de MR (CA) foi introduzida para mostrar a ação do gene de mRNA único e proteínas do fator de transcrição de genes.[58][59] Esta nova CA pode rastrear células com mRNA único, microRNA e vírus; resposta de tecido à inflamação em cérebros vivos.[60] Os MR relatam alteração na expressão gênica com correlação positiva com análise TaqMan, microscopia óptica e eletrônica.[61]
Spin e momento angular[editar | editar código-fonte]
Rigorosamente, núcleos não apresentam spin, mas sim momento angular (excepção feita somente ao núcleo do isótopo 1 do hidrogênio, que é constituído por um único próton). Embora o spin possa ser considerado um momento angular, por terem ambos as mesmas unidades e serem tratados por um formalismo matemático e físico semelhante, nem sempre o oposto ocorre. O spin é intrínseco, ao passo que objetos compostos tem momento angular extrínseco.
Contudo, motivos históricos e continuado costume levaram a esse abuso de linguagem, tolerado e talvez tolerável em textos não rigorosos. Um motivo a mais de complicação é o fato de que a moderna física de partículas considera que certas partículas, antes pensadas como elementares (e portanto possuindo spin), sejam compostas (próton e nêutron compostos de quarks). Assim, fica um tanto impreciso o limite entre os casos onde se deva usar o termo spin e os casos onde se deva usar o termo momento angular.
Sequência spin-echo[editar | editar código-fonte]
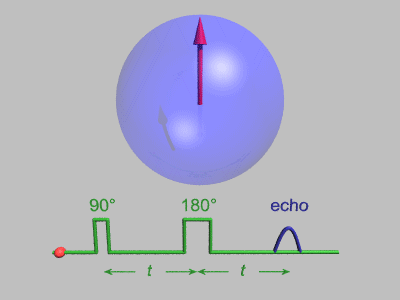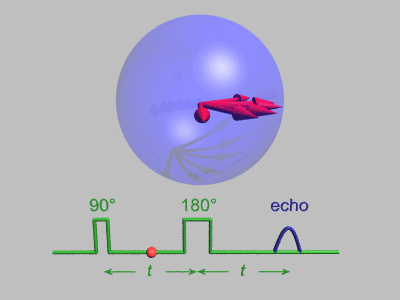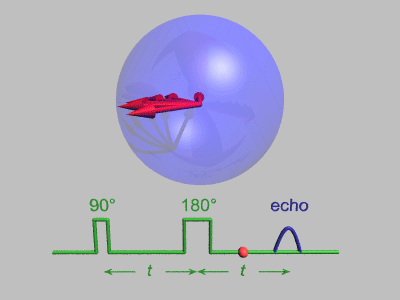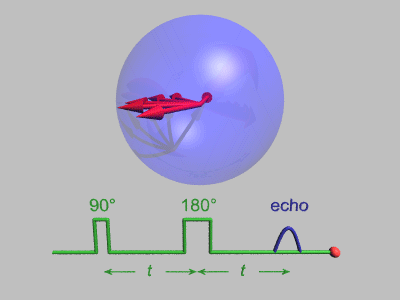
Em 1950, Erwin Hahn apresentou na Physical Review 80 o resultado de uma experiência sobre ressonância nuclear. Esse experimento é conhecido como “Spin Echo”.[6]
A sequência Spin-Echo de Hahn é descrita da seguinte forma:
sendo esta uma das sequência de pulsos mais importantes na espectroscopia de RMN. O experimento Spin-Echo causa o cancelamento de todos os efeitos que resulta de diferentes frequências de Larmor, incluindo os de deslocamentos químicos e efeito produzido pelo campo magnético não uniforme através da amostra.
A utilização do experimento de Spin–Echo facilita a medição do parâmetro T2, que está sujeito a dificuldades, mesmo no caso de um único conjunto de spins nucleares idênticos.
Este consiste em realizar a refocagem das isocromatas de spin através de pulsos de 90º repetidamente.
Em 1954, H. Y. Carr e E. M. Purcell publicaram na Physical Review 94 um trabalho que estendeu um pouco mais a sequência de pulsos de Hahn, conhecida como sequência de Carr-Purcell. Esta sequência de pulsos também gera eco e é consideralvelmente mais fácil de visualizar do que a sequência de Hahn.
A sequência de pulsos Carr-Purcell é realizada da seguinte forma
podemos visualizar esta sequência de pulso pelo gráfico em 3D adaptado do respectivo trabalho na figura.
Imageamento biológico[editar | editar código-fonte]
A técnica da ressonância magnética nuclear é usada em medicina e em biologia como meio de formar imagens internas de corpos humanos e de animais, bem como de seres microscópicos (como no caso da microscopia de RMN). É chamada de tomografia de ressonância magnética nuclear ou apenas de ressonância magnética. Consiste em aplicar em um paciente submetido a um campo magnético intenso, ondas com frequências iguais às dos núcleos (geralmente do 1H da água) dos tecidos do corpo que se quer examinar. Tais tecidos absorvem a energia em função da quantidade de água do tecido. Entretanto, para se localizar espacialmente o grupo de núcleos de hidrogênio, é preciso se empregar um meio de se diferenciar o campo, impondo-lhe gradientes segundo certas direções.
Para imageamento de uma amostra, é necessário que a aparelhagem coloque a aquisição de sinal em função da posição. Esta função matemática é de em , e essa informação é suprida através de aplicação de um campo magnético que apresenta um gradiente tridimensional. Assim, para cada posição da amostra, dentro da margem de erro resultante da resolução, a aquisição é levemente diferente. O resultado então é tratado pela transformada de Fourier (especificamente FFT: Fast Fourier Transform), sendo resolvido a partir daí no espaço e não mais em frequência.
Os SPINs, tem o seu movimento em seu próprio eixo, quando um átomo de hidrogênio é posto em um campo magnético, os spins que estão dentro dele tendem a se orientar em direção ao campo magnético paralelo.
Técnicas de RMN no estado sólido[editar | editar código-fonte]
Ângulo mágico girando[editar | editar código-fonte]

Em 1959, Irving J. Lowe divulgou na Physical Review Letters, uma experiência de RMN utilizando amostras de Teflon e CaF2 sob rotações rápidas.[6]
Através deste experimento Lowe conseguira observar as linhas de RMN das amostras sólidas rodando a uma velocidade angular ωs e consequentemente apresentavam bandas laterais “aguçadas ou finas'' como ele dizia à frequências ωs.
Estas bandas laterais provinham da modulação da linha de ressonância que por sua vez eram adicionados as extremidades da linha de RMN. A contribuição do movimento das extremidades era fraca para ser observada, por causa dos movimentos internos que possuem uma vasta frequência espectral.
Esta técnica que ele utilizara foi antes divulgada por ele juntamente com Norberg em 1957 na Physical Review.
A medida das linhas das amostras girante foi realizada pela observação do FID utilizando como standard o aparelho de Spin-Echo de Hahn. As amostras foram giradas a 7 Kc (Kcycles/sec = kHz) usando rotores (7 mm) em drivers com turbinas de ar. A orientação da amostra pode ser variada em relação ao campo aplicado H em θH = θº 54,7º e 90º.
Os resultados mostraram que os espectros de ressonância para as amostras girantes (spinning) e não-girantes (nonspinning) apresentaram os mesmos decaimentos de indução livre (FDI),[nota 1] quando colocadas a um ângulo θH = θº ,mas quando estas foram colocadas sob θH = 54,7º os FIDs apresentam uma série de “echos rotacionais”a Ts,2Ts,etc. Para θH = 90º , o FID foi visto como uma linha não resolvida.[6]
Dupla ressonância[editar | editar código-fonte]
Em 1962, os físicos S.R. Hartmann e Erwin Hahn publicaram o célebre trabalho sobre "dupla ressonância" na Physical Review , mais tarde referenciada como “condição de Hartmann-Hahn”, que estabelece a relação entre um núcleo abundante (a) e um núcleo raro (b) no eixo rotatório para o mesmo tempo da dupla ressonância.
Polarização cruzada[editar | editar código-fonte]

Em 1973 Pines, Gibby e Waugh divulgaram um trabalho no Journal of Chemical Physics, o qual tratava em relatar o ganho de sensibilidade de um dado núcleo raro S através da transferência de polarização de um núcleo abundante I.
A técnica Polarização Cruzada - CP, consiste em otimizar os problemas relacionados com baixa abundância natural de núcleos raros.
O efeito do CP é provocar um aumento da magnetização de núcleos raros do tipo 13C em favor de núcleos abundantes, 1H, facilitando (diminuindo) a relaxação (RMN) spin-rede (T1) e melhorando (aumentando) a relação sinal/ruído , num fator γH/γC ≈ 4 .
Neste caso os núcleos abundantes aproximam-se de um reservatório térmico, e a sua transferência de polarização para o núcleo raro S se dá por processo favorável, de natureza termodinâmica.

Favorecendo um sistema de alta magnetização alinhada a um baixo campo magnético B0. Este contato térmico é estabelecido no chamado sistema girante de coordenadas, quando a condição de Hartmann-Hahn, γHB1H=γCB1C é satisfeita através da aplicação de campos de r.f (radiofrequência) para o núcleo simultaneamente.
Quando ambos os sistemas de spins apresentarem as mesmas frequências angulares ω1 (=γB1) obtidas através do ajuste da intensidade B1 no sistema de coordenadas girantes, a condição de Hartmann-Hahn é satisfeita, e a transferência de polarização é permitida.[6]
O sistema girante de coordenadas é um sistema que gira com a frequência de ressonância de cada núcleo em particular em torno de . Em tal sistema, a frequência de precessão de Larmor γB0 é eliminada, o que significa o desaparecimento de .
O único campo magnético que age sobre cada spin é o campo de RF estático, neste referencial, e tem o mesmo papel de no sistema de referência do laboratório.[6]
Neste caso, pode-se observar que a condição de Hartmann-Hahn significa que os dois núcleos terão a mesma frequência de Larmor em seus respectivos sistemas girantes de coordenadas, ω1H = ω1C
Desacoplamento dipolar[editar | editar código-fonte]

Spins nucleares apresentam um momento de dipolo, que interage com o momento de dipolo de outros núcleos (acoplamento dipolar). A magnitude da interação é dependente dos tipos de rotação (spin), a distância internuclear e a orientação do vetor que liga os dois spins nucleares em relação ao campo magnético externo B. O acoplamento máximo dipolar é dada pelo acoplamento dipolar constante , representado por d
,
em que r é a distância entre os núcleos, e γ1 e γ2 são os quocientes giromagnéticos[nota 2] dos núcleos. Em um forte campo magnético, o acoplamento dipolar depende da orientação do vetor internuclear com o campo magnético externo
.
Consequentemente, dois núcleos com um vetor de acoplamento dipolar a um ângulo de θm=54.7° a um forte campo magnético externo, o qual é o ângulo em que D se torna zero, tem acoplamento dipolar equivalente a zero . θm é chamado de ângulo mágico.
Formação das grandes imagens de ressonância magnética[editar | editar código-fonte]

Em 1971, o médico Raymond Vahan Damadian mostrou que diferentes tipos de tecidos e tumores possuíam diferentes tempos de relaxação (RMN). Este fato motivou os cientistas a considerarem a ressonância magnética uma técnica de elevado potencial diagnóstico e a procurarem meios de obter imagens do interior de corpos opacos.
Para construir uma imagem o elemento chave é saber de que região da amostra provém cada sinal de RMN adquirido. Aproveitando a relação de Larmor, Lauterbur , em 1973, usou um campo magnético com comportamento espacial conhecido para “codificar” o sinal de ressonância magnética. Desta forma foram obtidas as primeiras imagens de RMN , com o método de back projection, já utilizado na tomografia de raio X.
Em 1975, Richard Robert Ernst e colaboradores propuseram realizar uma codificação completa usando o formalismo da transformada de Fourier (TF), levando em consideração a frequência e a fase do sinal. Pouco depois, muitos outros trabalhos pioneiros mostraram, na prática, a viabilidade desta técnica usada até hoje.[6]
- Gradientes de campo magnético
O novo elemento codificador do sinal é um campo magnético não homogêneo e variável no tempo. Este campo tem uma componente paralela ao B0 (eixo z) com dependência espacial linear, que é sobreposta ao mesmo. Para poder representar as 3 orientações espaciais de um objeto, são utilizados os gradientes de campo nas 3 direções ortogonais.
As bobinas encarregadas de gerar esta distribuição de campo são denominadas bobinas de gradiente. Desta maneira, a componente z do campo resultante fica expressa como:
Assim, cada conjunto de spins localizados em uma posição diferente, terá uma frequência de precessão diferente, dada pela expressão:
A frequência de precessão não é a única variável que passa a ter uma dependência espacial. Após um dado tempo de aplicação de qualquer gradiente, o acúmulo de fase também será uma função da posição. Deste modo, estas duas variáveis formam as bases da codificação espacial.
O gradiente de campo introduzido corresponde ao termo .
Sequências[editar | editar código-fonte]
Uma sequência de RM (Ressonância Magnética) é uma configuração particular de pulsos de radiofrequência e gradientes, resultando em uma imagem específica[62]. O ponderamento T1 e T2 também podem ser descritos como sequências de RM.
Tabela de visão geral[editar | editar código-fonte]
Esta tabela não inclui sequências incomuns e experimentais.
| Grupo | Sequência | Abreviatura | Física | Distinções clínicas principais | Exemplo |
|---|---|---|---|---|---|
| Eco de spin | Ponderado em T1 | T1 | Medição da relaxação spin-lattice usando um tempo de repetição (TR) curto e tempo de eco (TE) curto. |
Base padrão e comparação para outras sequências. |
 |
| Ponderado em T2 | T2 | Medição da relaxação spin-spin usando TR e TE longos |
|
 | |
| Ponderado em densidade de prótons | PD | TR longo (para reduzir T1) e TE curto (para minimizar T2). | Doenças articulares e lesões. [66]
|
 | |
| Eco de gradiente (GRE) | Precessão livre de estado constante | SSFP | Manutenção de uma magnetização transversal residual estável ao longo de ciclos sucessivos. | Criação de vídeos de RM cardíaca.[68] |  |
| T2 efetivo ou "T2-estrela" | T2* | Eco de gradiente lembrado estragado (GRE) com tempo de eco longo e ângulo de inclinação pequeno. | Sinal baixo em depósitos de hemosiderina e hemorragias.[69] |  | |
| Ponderado em susceptibilidade | SWI | Eco de gradiente (GRE), totalmente compensado para o fluxo, tempo de eco longo, combina imagem de fase com imagem de magnitude. | Detecção de pequenas quantidades de hemorragia ou cálcio.[70] |  | |
| Recuperação de inversão | Inversão de tau curto | STIR | Supressão de gordura, definindo um tempo de inversão onde o sinal da gordura é zero. | Sinal alto em casos de edema, como em fraturas por estresse mais graves.[71] Canelite, por exemplo. |  |
| Recuperação de inversão atenuada a fluido | FLAIR | Supressão de fluidos, definindo um tempo de inversão que anula os fluidos. | Sinal alto em casos de infarto lacunar, placas de esclerose múltipla (EM), hemorragia subaracnóidea e meningite.[72] |  | |
| Recuperação de inversão dupla | DIR | Supressão simultânea do líquido cefalorraquidiano e da matéria branca por dois tempos de inversão. | Sinal alto em casos de placas de esclerose múltipla.[73] |  | |
| Ponderado em difusão (DWI) | Convencional | DWI | Medição do movimento browniano das moléculas de água. | Sinal alto dentro de minutos após um infarto cerebral.[74] | 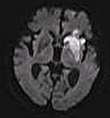 |
| Coeficiente de difusão aparente | ADC | Ponderamento reduzido em T2, usando várias imagens convencionais de DWI com diferentes ponderações de DWI, sendo a mudança correspondente à difusão. | Sinal baixo minutos após um infarto cerebral.[75] |  | |
| Tensor de difusão | DTI | Principalmente traçografia, com um movimento browniano geral maior das moléculas de água nas direções das fibras nervosas. |  | ||
| Ponderado em perfusão (PWI) | Susceptibilidade dinâmica contrastada | DSC | Medidas de mudanças ao longo do tempo na perda de sinal induzida por suscetibilidade devido à injeção de contraste de gadolínio.[78] |
|
 |
| Marcação de spin arterial | ASL | Marcação magnética do sangue arterial abaixo da área de imagem, que posteriormente entra na região de interesse.[80] Não requer contraste de gadolínio.[81] | |||
| Realce de contraste dinâmico | DCE | Medidas de mudanças ao longo do tempo no encurtamento da relaxação spin-lattice (T1) induzido por um bolo de contraste de gadolínio.[82] | O aumento rápido do contraste de gadolínio, juntamente com outras características, sugere malignidade. [83] |  | |
| Ressonância Magnética Funcional (fMRI) | Imagem dependente do nível de oxigênio no sangue | BOLD | Mudanças na magnetização dependente da saturação de oxigênio da hemoglobina refletem a atividade tecidual.[84] | Localização da atividade cerebral ao executar uma tarefa atribuída (por exemplo, falar, mover os dedos) antes da cirurgia, também usado na pesquisa de cognição.[85] |  |
| Angiografia e venografia por Ressonância Magnética (MRA) | Voo de tempo | TOF | O sangue que entra na área de imagem ainda não está saturado magneticamente, dando um sinal muito mais alto ao usar tempo de eco curto e compensação de fluxo. | Detecção de aneurisma, estenose ou dissecção.[86] |  |
| Ressonância magnética com contraste de fase | PC-MRA | Dois gradientes com magnitude igual, mas direção oposta, são usados para codificar uma mudança de fase, que é proporcional à velocidade das rotações.[87] | Detecção de aneurisma, estenose ou dissecção.[88] |  |
Economia[editar | editar código-fonte]
No Reino Unido, o preço de um scanner clínico de 1,5-tesla MRI é de cerca de £ 920,000 / US $ 1,4 milhão, com o custo de manutenção da vida em geral semelhante ao custo de compra.[89] Nos Países Baixos, o scanner MRI médio custa cerca de 1 milhão[90] de euros, com uma RM de 7-T que foi utilizada pelo UMC Utrecht em dezembro de 2007, custando 7 milhões de euros.[91] A construção de conjuntos de MRI pode custar até US $ 500.000/€ 370.000 ou mais, dependendo do escopo do projeto. Os sistemas de RMN pré-polarização (PMRI) que utilizam eletroímãs resistivos mostraram-se promissores como uma alternativa de baixo custo e possuem vantagens específicas para a imagem conjunta perto de implantes metálicos, no entanto, provavelmente não são adequados para aplicações rotineiras de todo o corpo ou de neuroimagem.[92][93]

Os scanners de ressonância magnética tornaram-se fontes importantes de receitas para os prestadores de cuidados de saúde nos EUA. Isso é devido a taxas favoráveis de reembolso de seguradoras e programas do governo federal. O reembolso de seguro é fornecido em dois componentes, uma carga de equipamento para o desempenho real e operação da varredura de MRI e uma cobrança profissional pela revisão do radiologista das imagens e/ou dados. No Nordeste dos EUA, uma carga de equipamento pode ser de US $ 3.500/€ 2.600[94] e uma taxa profissional pode ser de US $ 350/€ 260, embora as taxas reais recebidas pelo proprietário do equipamento e pelo médico intérprete geralmente sejam significativamente menores e dependem das taxas negociadas com companhias de seguros ou determinado pelo cronograma de taxas do Medicare. Por exemplo, um grupo de cirurgia ortopedista em Illinois faturou uma taxa de US $ 1.116/€ 825 para uma RM de joelho em 2007, mas o reembolso do Medicare em 2007 foi de apenas US $ 470,91/€ 350.[95] Muitas companhias de seguros exigem aprovação antecipada de um procedimento de ressonância magnética como condição para a cobertura.
Nos EUA, a Lei de redução de déficit de 2005 reduziu significativamente as taxas de reembolso pagas pelos programas federais de seguros para o componente de equipamentos de muitas varreduras, mudando a paisagem econômica. Muitas seguradoras privadas seguiram o exemplo.
Nos Estados Unidos, uma ressonância magnética do cérebro com e sem contraste faturado à Parte B do Medicare implica, em média, um pagamento técnico de US $ 403/€ 300 e um pagamento separado ao radiologista de US $ 93/€ 70.[96] Na França, o custo de um exame de ressonância magnética é de aproximadamente € 150/US $ 205. Isso abrange três varreduras básicas, incluindo uma com um agente de contraste intravenoso, bem como uma consulta com o técnico e um relatório escrito ao médico do paciente. No Japão, o custo de um exame de ressonância magnética (excluindo o custo de material de contraste e filmes) varia de US $ 155/115 a US $ 180/€ 133, com uma taxa profissional de radiologista adicional de US $ 17/€ 12,50.[97] Na Índia, o custo de um exame de ressonância magnética, incluindo a taxa para a opinião do radiologista, é de aproximadamente Rs 3000-4000 (€ 37-49/US $ 50-60), excluindo o custo do material de contraste. No Reino Unido, o preço de varejo de uma varredura de MRI varia em particular entre £ 350 e £ 700 (€ 405-810).[98]
Uso excessivo[editar | editar código-fonte]
As sociedades médicas emitem diretrizes para quando os médicos devem usar a ressonância magnética em pacientes e recomendar contra o uso excessivo. A ressonância magnética pode detectar problemas de saúde ou confirmar um diagnóstico, mas as sociedades médicas geralmente recomendam que a ressonância magnética não seja o primeiro procedimento para criar um plano para diagnosticar ou gerenciar a queixa de um paciente. Um caso comum é usar a ressonância magnética para buscar uma causa de dor lombar; o American College of Physicians, por exemplo, recomenda este procedimento como improvável, e que resulte em um resultado positivo para o paciente.[99][100]
Ver também[editar | editar código-fonte]
- Lista de medicinas nucleares
- Imagem médica
- Ressonância magnética nuclear (NMR)
- Neuroimagem
- Relaxação (NMR)
Notas
- ↑ Na RMN de Fourier, um decaimento de indução livre (FID) é o sinal de RMN observável gerado pelo não equilíbrio do spin nuclear sobre a precessão de magnetização do campo magnético (convencionalmente ao longo da coordenada z). Esta magnetização não equilibrada pode ser induzida, em geral, através da aplicação de um impulso de rádio-frequência ressonante perto da frequência de Larmor dos spins nucleares.
- ↑ Na física, o rácio giromagnético de uma partícula ou de um sistema é a razão entre o seu momento de dipolo magnético ao seu momento angular, e é muitas vezes indicado pelo símbolo γ, gama.
Referências
- ↑ Smith-Bindman R; Miglioretti DL; Johnson E; Lee C; Feigelson HS; Flynn M; Greenlee RT; Kruger RL; Hornbrook MC; et al. (2012). «Use of diagnostic imaging studies and associated radiation exposure for patients enrolled in large integrated health care systems, 1996–2010». JAMA. 307 (22): 2400–9. PMC 3859870
 . PMID 22692172. doi:10.1001/jama.2012.5960
. PMID 22692172. doi:10.1001/jama.2012.5960
- ↑ «Health at a glance 2009 OECD indicators». OECD. Health at a Glance. Health at a Glance. 2009. ISBN 9789264061538. ISSN 1995-3992. doi:10.1787/health_glance-2009-en
- ↑ Lauterbur PC (1973). «Image Formation by Induced Local Interactions: Examples of Employing Nuclear Magnetic Resonance». Nature. 242 (5394): 190–1. Bibcode:1973Natur.242..190L. doi:10.1038/242190a0
- ↑ Rinck PA (2014). «The history of MRI» 8th ed. Magnetic Resonance in Medicine
- ↑ Mansfield P; Grannell, P (1975). «Diffraction and microscopy in solids and liquids by NMR». Physical Review B. 12 (9): 3618–3634. Bibcode:1975PhRvB..12.3618M. doi:10.1103/physrevb.12.3618
- ↑ a b c d e f g h i j k l m n o Bathista, André Luis Bonfim Bathista e Silva (2013). André Luis Bonfim .Bathista e Silva, ed. Elementos Históricos de Ressonância Magnética Nuclear (PDF). Ressonância Magnética Nuclear. 1 1 ed. Instituto de Física de São Carlos: [s.n.] 48 páginas
- ↑ IBS researchers performed world’s smallest MRI on single atoms Magnetic resonance imaging enables to scan the magnetic field of single atoms with unprecedented resolution. por Ashwini Sakharkar (2019)
- ↑ McRobbie, Donald W. (2007). MRI from picture to proton. Cambridge, UK ; New York: Cambridge University Press. ISBN 0-521-68384-X
- ↑ Sasaki M; Ehara S; Nakasato T; Tamakawa Y; Kuboya Y; Sugisawa M; Sato T (abril de 1990). «MR of the shoulder with a 0.2-T permanent-magnet unit». AJR Am J Roentgenol. 154 (4): 777–8. PMID 2107675. doi:10.2214/ajr.154.4.2107675
- ↑ McDermott, Robert; et al. «Microtesla MRI with a superconducting quantum interference device» (PDF). Proceedings of the National Academy of Sciences. 101: 7857–7861. Bibcode:2004PNAS..101.7857M. doi:10.1073/pnas.0402382101
- ↑ Zotev, Vadim; et al. «SQUID-based instrumentation for ultra-low-field MRI» (PDF)
- ↑ Vesanen, Panu; et al. «Hybrid ultra-low-field MRI and magnetoencephalography system based on a commercial whole-head neuromagnetometer». Magnetic Resonance in Medicine. 69: 1795–1804. doi:10.1002/mrm.24413
- ↑ a b c d e f g h «Magnetic Resonance Imaging». University of Wisconsin. Consultado em 14 de março de 2016. Arquivado do original em 10 de maio de 2017
- ↑ a b c d e f g h i j k l m n Keith A. Johnson. «Basic proton MR imaging. Tissue Signal Characteristics». Harvard Medical School. Consultado em 14 de março de 2016. Arquivado do original em 5 de março de 2016
- ↑ «MR Contrast Agents». 2014
- ↑ Murphy, K J; Brunberg, J A; Cohan, R H (1 de outubro de 1996). «Adverse reactions to gadolinium contrast media: a review of 36 cases.». American Journal of Roentgenology. 167 (4): 847–849. ISSN 0361-803X. doi:10.2214/ajr.167.4.8819369
- ↑ «ACR guideline». guideline.gov. 2005. Consultado em 19 de outubro de 2017. Arquivado do original em 29 de setembro de 2006
- ↑ Thomsen, H.S.; Morcos, S.K.; Dawson, P. «Is there a causal relation between the administration of gadolinium based contrast media and the development of nephrogenic systemic fibrosis (NSF)?». Clinical Radiology. 61 (11): 905–906. doi:10.1016/j.crad.2006.09.003
- ↑ «FDA Drug Safety Communication: New warnings for using gadolinium-based contrast agents in patients with kidney dysfunction». Information on Gadolinium-Based Contrast Agents. U.S. Food and Drug Administration. 23 de Dezembro de 2010. Consultado em 12 de Março de 2011
- ↑ «FDA Public Health Advisory: Gadolinium-containing Contrast Agents for Magnetic Resonance Imaging». fda.gov. Arquivado do original em 28 de setembro de 2006
- ↑ [1] Arquivado em 2013-01-17 no Wayback Machine
- ↑ «ismrm.org MRI Questions and Answers» (PDF). Consultado em 2 de agosto de 2010
- ↑ «Response to the FDA's, Nephrogenic Systemic Fibrosis Update1 — Radiology». Radiology.rsna.org. 23 de maio de 2007. Consultado em 2 de agosto de 2010. Arquivado do original em 19 de julho de 2012
- ↑ «Magnetic Resonance, a critical peer-reviewed introduction». European Magnetic Resonance Forum. Consultado em 17 de Novembro de 2014
- ↑ Hollingworth W; Todd CJ; Bell MI; Arafat Q; Girling S; Karia KR; Dixon AK (2000). «The diagnostic and therapeutic impact of MRI: an observational multi-centre study». Clin Radiol. 55 (11): 825–31. PMID 11069736. doi:10.1053/crad.2000.0546
- ↑ Husband, J (2008). Recommendations for Cross-Sectional Imaging in Cancer Management: Computed Tomography – CT Magnetic Resonance Imaging – MRI Positron Emission Tomography – PET-CT (PDF). [S.l.]: Royal College of Radiologists. ISBN 1 905034 13 X
- ↑ American Society of Neuroradiology (2013). «ACR-ASNR Practice Guideline for the Performance and Interpretation of Magnetic Resonance Imaging (MRI) of the Brain» (PDF)
- ↑ Nolen-Hoeksema, Susan (2014). Abnormal Psychology 6.ª ed. New York, NY: McGraw-Hill Education. p. 67
- ↑ Galloway, RL Jr. (2015). «Introduction and Historical Perspectives on Image-Guided Surgery». In: Golby, AJ. Image-Guided Neurosurgery. Amsterdam: Elsevier. pp. 3–4
- ↑ Tse, VCK; Kalani, MYS; Adler, JR (2015). «Techniques of Stereotactic Localization». In: Chin, LS; Regine, WF. Principles and Practice of Stereotactic Radiosurgery. New York: Springer. p. 28
- ↑ Saleh, H; Kassas, B (2015). «Developing Stereotactic Frames for Cranial Treatment». In: Benedict, SH; Schlesinger, DJ; Goetsch, SJ; Kavanagh, BD. Stereotactic Radiosurgery and Stereotactic Body Radiation Therapy. Boca Raton: CRC Press. pp. 156–159
- ↑ Khan, FR; Henderson, JM (2013). «Deep Brain Stimulation Surgical Techniques». In: Lozano, AM; Hallet, M. Brain Stimulation: Handbook of Clinical Neurology. 116. Amsterdam: Elsevier. pp. 28–30
- ↑ Arle, J (2009). «Development of a Classic: the Todd-Wells Apparatus, the BRW, and the CRW Stereotactic Frames». In: Lozano, AM; Gildenberg, PL; Tasker, RR. Textbook of Stereotactic and Functional Neurosurgery. Berlin: Springer-Verlag. pp. 456–461
- ↑ Sharan, AD; Andrews, DW (2003). «Stereotactic Frames: Technical Considerations». In: Schulder, M; Gandhi, CD. Handbook of Stereotactic and Functional Neurosurgery. New York: Marcel Dekker. pp. 16–17
- ↑ Apuzzo, MLJ; Fredericks, CA (1988). «The Brown-Roberts-Wells System». In: Lunsford, LD. Modern Stereotactic Neurosurgery. Boston: Martinus Nijhoff Publishing. pp. 63–77
- ↑ Brown RA; Nelson JA (2012). «Invention of the N-localizer for stereotactic neurosurgery and its use in the Brown-Roberts-Wells stereotactic frame». Neurosurgery. 70 (2 Supplement Operative): 173–176. PMID 22186842. doi:10.1227/NEU.0b013e318246a4f7
- ↑ Brown RA, Nelson JA (2016). «The invention and early history of the N-localizer for stereotactic neurosurgery». Cureus. 8 (6): e642. PMC 4959822
 . PMID 27462476. doi:10.7759/cureus.642
. PMID 27462476. doi:10.7759/cureus.642
- ↑ Brown RA (2015). «The mathematics of three N-localizers used together for stereotactic neurosurgery». Cureus. 7 (10): e341. PMC 4636133
 . PMID 26594605. doi:10.7759/cureus.341
. PMID 26594605. doi:10.7759/cureus.341
- ↑ Brown RA (2015). «The mathematics of four or more N-localizers for stereotactic neurosurgery». Cureus. 7 (10): e349. PMC 4641741
 . PMID 26623204. doi:10.7759/cureus.349
. PMID 26623204. doi:10.7759/cureus.349
- ↑ Leksell L; Leksell D; Schwebel J (1985). «Stereotaxis and nuclear magnetic resonance». Journal of Neurology, Neurosurgery & Psychiatry. 48 (1): 14–18. PMC 1028176
 . PMID 3882889. doi:10.1136/jnnp.48.1.14
. PMID 3882889. doi:10.1136/jnnp.48.1.14
- ↑ Thomas DG; Davis CH; Ingram S; Olney JS; Bydder GM; Young IR (1986). «Stereotaxic biopsy of the brain under MR imaging control». AJNR American Journal of Neuroradiology. 7 (1): 161–163. PMID 3082131
- ↑ Heilbrun MP; Sunderland PM; McDonald PR; Wells TH Jr.; Cosman E; Ganz E (1987). «Brown-Roberts-Wells stereotactic frame modifications to accomplish magnetic resonance imaging guidance in three planes». Applied Neurophysiology. 50 (1–6): 143–152. PMID 3329837. doi:10.1159/000100700
- ↑ «ACCF/ACR/SCCT/SCMR/ASNC/NASCI/SCAI/SIR 2006 Appropriateness Criteria for Cardiac Computed Tomography and Cardiac Magnetic Resonance Imaging». Journal of the American College of Radiology. 3 (10): 751–771. 2006. ISSN 1546-1440. doi:10.1016/j.jacr.2006.08.008
- ↑ Helms, C (2008). Musculoskeletal MRI. [S.l.]: Saunders. ISBN 1416055347
- ↑ Frydrychowicz A; Lubner MG; Brown JJ; Merkle EM; Nagle SK; Rofsky NM; Reeder SB (2012). «Hepatobiliary MR imaging with gadolinium-based contrast agents». J Magn Reson Imaging. 35 (3): 492–511. PMC 3281562
 . PMID 22334493. doi:10.1002/jmri.22833
. PMID 22334493. doi:10.1002/jmri.22833
- ↑ Sandrasegaran K; Lin C; Akisik FM; Tann M (2010). «State-of-the-art pancreatic MRI». AJR Am J Roentgenol. 195 (1): 42–53. PMID 20566796. doi:10.2214/ajr.195.3_supplement.0s42
- ↑ Masselli G; Gualdi G (2012). «MR imaging of the small bowel». Radiology. 264 (2): 333–48. PMID 22821694. doi:10.1148/radiol.12111658
- ↑ Zijta FM; Bipat S; Stoker J (2010). «Magnetic resonance (MR) colonography in the detection of colorectal lesions: a systematic review of prospective studies». Eur Radiol. 20 (5): 1031–46. PMC 2850516
 . PMID 19936754. doi:10.1007/s00330-009-1663-4
. PMID 19936754. doi:10.1007/s00330-009-1663-4
- ↑ Haacke, E Mark; Brown, Robert F; Thompson, Michael; Venkatesan, Ramesh (1999). Magnetic resonance imaging: Physical principles and sequence design. New York: J. Wiley & Sons. ISBN 0-471-35128-8[falta página]
- ↑ Rosen, Yael; Lenkinski, Robert E. (1 de julho de 2007). «Recent advances in magnetic resonance neurospectroscopy». Neurotherapeutics (em inglês). 4 (3): 330–345. ISSN 1933-7213. doi:10.1016/j.nurt.2007.04.009
- ↑ Golder, W. (2004). «Magnetic Resonance Spectroscopy in Clinical Oncology». Oncology Research and Treatment (em english). 27 (3): 304–309. ISSN 2296-5270. doi:10.1159/000077983
- ↑ I Uyanik, P Lindner, D Shah, N Tsekos I Pavlidis (2013) Applying a Level Set Method for Resolving Physiologic Motions in Free-Breathing and Non-gated Cardiac MRI. FIMH, 2013, [2] Arquivado em 22 de julho de 2018, no Wayback Machine.
- ↑ Cline, Harvey E.; Schenck, John F.; Hynynen, Kullervo; Watkins, Ronald D.; Souza, Steven P.; Jolesz, Ferenc A. «MR-Guided Focused Ultrasound Surgery». Journal of Computer Assisted Tomography. 16 (6): 956–965. doi:10.1097/00004728-199211000-00024
- ↑ «Hyperpolarized Noble Gas MRI Laboratory: Hyperpolarized Xenon MR Imaging of the Brain». Harvard Medical School. Consultado em 26 de julho de 2017
- ↑ Hurd, Ralph E; John, Boban K. «Gradient-enhanced proton-detected heteronuclear multiple-quantum coherence spectroscopy». Journal of Magnetic Resonance (1969). 91 (3): 648–653. doi:10.1016/0022-2364(91)90395-a
- ↑ Brown, R.A.; Venters, R.A.; Tang, P.P.P.Z.; Spicer, L.D. «A Test for Scaler Coupling between Heteronuclei Using Gradient-Enhanced Proton-Detected HMQC Spectroscopy». Journal of Magnetic Resonance, Series A. 113 (1): 117–119. doi:10.1006/jmra.1995.1064
- ↑ Xue, Shenghui; Qiao, Jingjuan; Pu, Fan; Cameron, Mathew; Yang, Jenny J. (1 de março de 2013). «Design of a novel class of protein-based magnetic resonance imaging contrast agents for the molecular imaging of cancer biomarkers». Wiley Interdisciplinary Reviews: Nanomedicine and Nanobiotechnology (em inglês). 5 (2): 163–179. ISSN 1939-0041. doi:10.1002/wnan.1205
- ↑ Liu CH; Kim YR; Ren JQ; Eichler F; Rosen BR; Liu PK (2007). «Imaging cerebral gene transcripts in live animals». J. Neurosci. 27 (3): 713–22. PMC 2647966
 . PMID 17234603. doi:10.1523/JNEUROSCI.4660-06.2007
. PMID 17234603. doi:10.1523/JNEUROSCI.4660-06.2007
- ↑ Liu CH; Ren J; Liu CM; Liu PK (2014). «Intracellular gene transcription factor protein-guided MRI by DNA aptamers in vivo». FASEB J. 28 (1): 464–73. PMID 24115049. doi:10.1096/fj.13-234229
- ↑ Liu CH; You Z; Liu CM; Kim YR; Whalen MJ; Rosen BR; Liu PK (2009). «Diffusion-weighted magnetic resonance imaging reversal by gene knockdown of matrix metalloproteinase-9 activities in live animal brains». J. Neurosci. 29 (11): 3508–17. PMC 2726707
 . PMID 19295156. doi:10.1523/JNEUROSCI.5332-08.2009
. PMID 19295156. doi:10.1523/JNEUROSCI.5332-08.2009
- ↑ Liu CH; Yang J; Ren JQ; Liu CM; You Z; Liu PK (2013). «MRI reveals differential effects of amphetamine exposure on neuroglia in vivo». FASEB J. 27 (2): 712–24. PMC 3545538
 . PMID 23150521. doi:10.1096/fj.12-220061
. PMID 23150521. doi:10.1096/fj.12-220061
- ↑ Murphy, Andrew; Gaillard, Frank (4 de junho de 2015). «MRI sequences (overview)». Radiopaedia.org. Radiopaedia.org. Consultado em 30 de outubro de 2023
- ↑ a b c d Isa, Tatebayashi (janeiro de 1996). «5514957 Positioning in magnetic resonance imaging». Magnetic Resonance Imaging (10): XII. ISSN 0730-725X. doi:10.1016/s0730-725x(97)81775-4. Consultado em 30 de outubro de 2023
- ↑ a b c d Ozdamar Erol, Yasemin; Inanc, Merve (2016). «Reverse Pseudohypopyon». International Journal of Clinical & Medical Imaging (05). ISSN 2376-0249. doi:10.4172/2376-0249.1000465. Consultado em 30 de outubro de 2023
- ↑ Jones, Jeremy; Gaillard, Frank (4 de maio de 2020). «3D fast spin echo (MRI sequence)». Radiopaedia.org. Radiopaedia.org. Consultado em 30 de outubro de 2023
- ↑ du Plessis, L.H.; Elgar, D.; du Plessis, J.L. (janeiro de 2008). «Southern African scorpion toxins: An overview». Toxicon (1): 1–9. ISSN 0041-0101. doi:10.1016/j.toxicon.2007.08.018. Consultado em 30 de outubro de 2023
- ↑ Lefevre, Nicolas; Naouri, Jean Francois; Herman, Serge; Gerometta, Antoine; Klouche, Shahnaz; Bohu, Yoann (2016). «A Current Review of the Meniscus Imaging: Proposition of a Useful Tool for Its Radiologic Analysis». Radiology Research and Practice (em inglês): 1–25. ISSN 2090-1941. doi:10.1155/2016/8329296. Consultado em 30 de outubro de 2023
- ↑ Rock, Patrick; Weerakkody, Yuranga (19 de outubro de 2009). «Steady-state free precession MRI». Radiopaedia.org. Radiopaedia.org. Consultado em 30 de outubro de 2023
- ↑ Chavhan, Govind B.; Babyn, Paul S.; Thomas, Bejoy; Shroff, Manohar M.; Haacke, E. Mark (setembro de 2009). «Principles, Techniques, and Applications of T2*-based MR Imaging and Its Special Applications». RadioGraphics (em inglês) (5): 1433–1449. ISSN 0271-5333. doi:10.1148/rg.295095034. Consultado em 30 de outubro de 2023
- ↑ Gaillard, Frank (24 de maio de 2011). «Susceptibility weighted imaging». Radiopaedia.org. Radiopaedia.org. Consultado em 30 de outubro de 2023
- ↑ Berger, Ferco H.; de Jonge, Milko C.; Maas, Mario (abril de 2007). «Stress fractures in the lower extremity». European Journal of Radiology (1): 16–26. ISSN 0720-048X. doi:10.1016/j.ejrad.2007.01.014. Consultado em 30 de outubro de 2023
- ↑ Baba, Yahya; Niknejad, Mohammad (16 de fevereiro de 2013). «Fluid attenuated inversion recovery». Radiopaedia.org. Radiopaedia.org. Consultado em 30 de outubro de 2023
- ↑ Murphy, Andrew; Abdrabou, Ahmed (11 de novembro de 2014). «Double inversion recovery sequence». Radiopaedia.org. Radiopaedia.org. Consultado em 30 de outubro de 2023
- ↑ Weerakkody, Yuranga; Gaillard, Frank (29 de dezembro de 2010). «Structure of radiopaedia». Radiopaedia.org. Radiopaedia.org. Consultado em 30 de outubro de 2023
- ↑ An, Hongyu; Ford, Andria L.; Vo, Katie; Powers, William J.; Lee, Jin-Moo; Lin, Weili (maio de 2011). «Signal Evolution and Infarction Risk for Apparent Diffusion Coefficient Lesions in Acute Ischemic Stroke Are Both Time- and Perfusion-Dependent». Stroke (em inglês) (5): 1276–1281. ISSN 0039-2499. doi:10.1161/STROKEAHA.110.610501. Consultado em 30 de outubro de 2023
- ↑ Leite, Claudia da Costa; Leite, Claudia da Costa; Castillo, Mauricio, eds. (2016). «13 Diffusion Weighted Imaging and Diffusion Tensor Imaging in Spine and Spinal Cord Diseases». Stuttgart: Georg Thieme Verlag. Consultado em 30 de outubro de 2023
- ↑ Chua, Terence C; Wen, Wei; Slavin, Melissa J; Sachdev, Perminder S (fevereiro de 2008). «Diffusion tensor imaging in mild cognitive impairment and Alzheimerʼs disease: a review:». Current Opinion in Neurology (em inglês) (1): 83–92. ISSN 1350-7540. doi:10.1097/WCO.0b013e3282f4594b. Consultado em 30 de outubro de 2023
- ↑ Lee, Matthew; Gaillard, Frank (25 de março de 2016). «Dynamic susceptibility contrast (DSC) MR perfusion». Radiopaedia.org. Radiopaedia.org. Consultado em 30 de outubro de 2023
- ↑ Chen, Feng (2012). «Magnetic resonance diffusion-perfusion mismatch in acute ischemic stroke: An update». World Journal of Radiology (em inglês) (3). 63 páginas. ISSN 1949-8470. doi:10.4329/wjr.v4.i3.63. Consultado em 30 de outubro de 2023
- ↑ Jain, Rajan; Essig, Marco, eds. (2016). «6 Perfusion imagingarterial spin labeling (ASL)Arterial spin labeling (ASL)Perfusion Imaging: Arterial Spin Labeling». Stuttgart: Georg Thieme Verlag. ISBN 978-1-60406-806-1. Consultado em 30 de outubro de 2023
- ↑ Rock, Patrick; Gaillard, Frank (25 de março de 2016). «Arterial spin labelling MR perfusion». Radiopaedia.org. Radiopaedia.org. Consultado em 30 de outubro de 2023
- ↑ Murphy, Andrew; Gaillard, Frank (25 de março de 2016). «Dynamic contrast enhanced (DCE) MR perfusion». Radiopaedia.org. Radiopaedia.org. Consultado em 30 de outubro de 2023
- ↑ Turnbull, Lindsay W. (janeiro de 2009). «Dynamic contrast-enhanced MRI in the diagnosis and management of breast cancer». NMR in Biomedicine (em inglês) (1): 28–39. doi:10.1002/nbm.1273. Consultado em 30 de outubro de 2023
- ↑ Chou, I-han (fevereiro de 2008). «Read my mind». Nature Physics (S1): S17–S17. ISSN 1745-2473. doi:10.1038/nphys874. Consultado em 30 de outubro de 2023
- ↑ Gaillard, Frank (18 de fevereiro de 2017). «Radiopaedia identification number (rID)». Radiopaedia.org. Radiopaedia.org. Consultado em 30 de outubro de 2023
- ↑ Duerinckx, André J. «Alternatives to Coronary MRA». New York: Springer-Verlag: 272–273. ISBN 0-387-94959-3. Consultado em 30 de outubro de 2023
- ↑ Botz, Balint; Ballinger, J. (5 de março de 2013). «Phase contrast imaging». Radiopaedia.org. Radiopaedia.org. Consultado em 30 de outubro de 2023
- ↑ AndréJ, Duerinckx. «Second-Generation Coronary MRA Techniques». New York: Springer-Verlag: 184–192. ISBN 0-387-94959-3. Consultado em 30 de outubro de 2023
- ↑ «Managing high value capital equipment in the NHS in England» (PDF). National Audit Office (United Kingdom). Consultado em 30 de Novembro de 2013. Arquivado do original (PDF) em 3 de Dezembro de 2013
- ↑ «MRI-scanner big financial success for Philips (Dutch)». Eindhovens Dagblad (ED). Consultado em 18 de Fevereiro de 2009
- ↑ «MRI scanner of €7 million in use(Dutch)». Medisch Contact. Consultado em 5 de Dezembro de 2007. Arquivado do original em 4 de setembro de 2015
- ↑ Morgan, Patrick; Conolly, Steven; Scott, Greig; Macovski, Albert (1 de outubro de 1996). «A readout magnet for prepolarized MRI». Magnetic Resonance in Medicine (em inglês). 36 (4): 527–536. ISSN 1522-2594. doi:10.1002/mrm.1910360405
- ↑ Blamire, A M (1 de agosto de 2008). «The technology of MRI — the next 10 years?». The British Journal of Radiology. 81 (968): 601–617. ISSN 0007-1285. doi:10.1259/bjr/96872829
- ↑ Stamford Hospital price quotation October 2008, Stamford CT US
- ↑ Goldstein, Wayne M.; Gordon, Alexander C.; Branson, Jill Jasperson; Simmons, Christopher; Berland, Kimberly; Willsey, Daniel S.; Andrews, Amanda L. (5–9 de Março de 2008). Over-Utilization of MRI in the Osteoarthritis Patient (PDF). Annual Meeting AAOS. San Francisco
- ↑ Current Procedural Terminology code #70553 "2010 Medicare Part B National Summary Data File" Arquivado em 14 de fevereiro de 2012, no Wayback Machine.. Data.gov, An Official Website of the United States Government.
- ↑ Ehara, Shigeru; Nakajima, Yasuo; Matsui, Osamu (1 de agosto de 2008). «Radiology in Japan in 2008». American Journal of Roentgenology. 191 (2): 328–329. ISSN 0361-803X. doi:10.2214/ajr.07.3940
- ↑ «Private MRI Scan». Fairfield.org.uk. Fairfield Independent Hospital. Consultado em 28 de março de 2017
- ↑ Consumer Reports; American College of Physicians. presented by ABIM Foundation. «Five Things Physicians and Patients Should Question» (PDF). Consumer Reports]. Choosing Wisely. Consultado em 14 de Agosto de 2012. Arquivado do original (PDF) em 24 de Junho de 2012
- ↑ Consumer Reports; American College of Physicians (Abril de 2012). presented by Annals of Internal Medicine. «Imaging tests for lower-back pain: Why you probably don't need them» (PDF). Consumer Reports. High Value Care. Consultado em 14 de Agosto de 2012
Leitura adicional[editar | editar código-fonte]
- TRTF/EMRF: The history of MRI (Peter A. Rinck, ed). url = http://www.magnetic-resonance.org/ch/20-01.html
- Guadalupe Portal; Aliosvi Rodriguez Whole body magnetic resonance imaging in early diagnosis in Trinidad BMJ (2010) ISSN 1756-1833 url = http://www.bmj.com/rapid-response/2011/12/19/re-whole-body-magnetic-resonance-imaging
- Ian L. Pykett (1 de maio de 1982). «NMR Imaging in Medicine» (PDF). Scientific American. 246 (5): 78–88. doi:10.1038/scientificamerican0582-78. Consultado em 13 de setembro de 2016. Arquivado do original (PDF) em 10 de março de 2016
- Perry Sprawls (2000). Magnetic Resonance Imaging Principles, Methods, and Techniques. [S.l.]: Medical Physics Publishing. ISBN 9780944838976
- Simon, Merrill; Mattson, James S (1996). The pioneers of NMR and magnetic resonance in medicine: The story of MRI. Ramat Gan, Israel: Bar-Ilan University Press. ISBN 0-9619243-1-4
- Haacke, E Mark; Brown, Robert F; Thompson, Michael; Venkatesan, Ramesh (1999). Magnetic resonance imaging: Physical principles and sequence design. New York: J. Wiley & Sons. ISBN 0-471-35128-8
- Lee SC; Kim K; Kim J; Lee S; Han Yi J; Kim SW; Ha KS; Cheong C (junho de 2001). «One micrometer resolution NMR microscopy». J. Magn. Reson. 150 (2): 207–13. Bibcode:2001JMagR.150..207L. PMID 11384182. doi:10.1006/jmre.2001.2319
- P Mansfield (1982). NMR Imaging in Biomedicine: Supplement 2 Advances in Magnetic Resonance. [S.l.]: Elsevier. ISBN 9780323154062
- Eiichi Fukushima (1989). NMR in Biomedicine: The Physical Basis. [S.l.]: Springer Science & Business Media. ISBN 9780883186091
- Bernhard Blümich; Winfried Kuhn (1992). Magnetic Resonance Microscopy: Methods and Applications in Materials Science, Agriculture and Biomedicine. [S.l.]: Wiley. ISBN 9783527284030
- Peter Blümer (1998). Peter Blümler, Bernhard Blümich, Robert E. Botto, Eiichi Fukushima, ed. Spatially Resolved Magnetic Resonance: Methods, Materials, Medicine, Biology, Rheology, Geology, Ecology, Hardware. [S.l.]: Wiley-VCH. ISBN 9783527296378
- Zhi-Pei Liang; Paul C. Lauterbur (1999). Principles of Magnetic Resonance Imaging: A Signal Processing Perspective. [S.l.]: Wiley. ISBN 9780780347236
- Franz Schmitt; Michael K. Stehling; Robert Turner (1998). Echo-Planar Imaging: Theory, Technique and Application. [S.l.]: Springer Berlin Heidelberg. ISBN 9783540631941
- Vadim Kuperman (2000). Magnetic Resonance Imaging: Physical Principles and Applications. [S.l.]: Academic Press. ISBN 9780080535708
- Bernhard Blümich (2000). NMR Imaging of Materials. [S.l.]: Clarendon Press. ISBN 9780198506836
- Jianming Jin (1998). Electromagnetic Analysis and Design in Magnetic Resonance Imaging. [S.l.]: CRC Press. ISBN 9780849396939
- Imad Akil Farhat; P. S. Belton; Graham Alan Webb; Royal Society of Chemistry (Great Britain) (2007). Magnetic Resonance in Food Science: From Molecules to Man. [S.l.]: Royal Society of Chemistry. ISBN 9780854043408
Ligações externas[editar | editar código-fonte]
- «Imageamento Fourier em Ressonância Nuclear Magnética»
- «A SHORT HISTORY OF MAGNETIC RESONANCE IMAGING FROM A EUROPEAN POINT OF VIEW»
- A short history of magnetic resonance imaging
- «RNM, Relaxamento e precessão; curvas T₁ e T₂, em inglês, indiano, árabe, hebraico, alemão, coreano e espanhol». animations
- Early Applications in Medicine and Biology
- The History of Magnetic Resonance Imaging
















![{\displaystyle \scriptstyle {\vec {B}}_{RF}=B_{1}(t){\big [}\cos(\omega t+\phi (t){\big )}{\hat {i}}+\sin {\big (}\omega t+\phi (t){\big )}{\hat {j}}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef8a6a11d3a12c431e2b767e6a90361acb930b65)













![{\displaystyle {\frac {N^{+}}{N^{-}}}=\exp {\Bigg [}{\frac {\gamma \hbar B_{0}}{kT}}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8456cf3a17572b5f7196baeacfab9fc303dffb59)










![{\displaystyle B_{I}={\Bigg [}{\frac {3(\mu _{1}.{\hat {r}}){\hat {r}}-\mu _{s}}{r^{3}}}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf26b541057cb2e07550207b77f83bbaea151844)

![{\displaystyle E={\Bigg [}{\frac {3(\mu _{I}.{\hat {r}})(\mu _{S}.{\hat {r}})-\mu _{I}.\mu _{S}}{r^{3}}}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bebfbe09da719c32cb4393f824fe366423a00892)
![{\displaystyle H_{D}=B_{1}=-\hbar \gamma _{I}\gamma _{S}{\Bigg [}{\frac {3(I.{\hat {r}})(S.{\hat {r}})-I.S}{r^{3}}}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fbb6f21f563ac5485f6578260c4ea079818c8d5)



















