Sólido platónico
Um sólido platônico ou poliedro regular, na geometria, é um poliedro convexo em que:
- todas as faces são formadas por polígonos regulares e congruentes (idênticas em forma e tamanho e com todos os ângulos e lados iguais entre si);
- o mesmo número de arestas encontra-se em todos os vértices, e portanto, os ângulos poliédricos são congruentes.[1]
São cinco os sólidos platônicos (sólidos que satisfazem essas condições) e os mesmos são descritos no décimo-terceiro livro de Os Elementos, de Euclides.[2]
| Tetraedro | Cubo | Octaedro | Dodecaedro | Icosaedro |
| Quatro faces | Seis faces | Oito faces | Doze faces | Vinte faces |
 |
 |
 |
 |
 |
Existem autores que definem sólidos platônicos de forma distinta.[nota 1][3]
Geômetras estudaram os sólidos platônicos por milhares de anos.[4] Os sólidos recebem este nome devido ao antigo filósofo grego Platão ter suposto em seu diálogo, o Timeu, que os elementos clássicos foram feitos com os sólidos regulares.[5]
História[editar | editar código-fonte]
Os sólidos platônicos são conhecidos desde a antiguidade. Têm sido sugerido que certas pedras arredondadas esculpidas pelos Neolíticos da Escócia representam estas formas; no entanto, essas bolas têm botões arredondados ao invés de ângulos poliédricos, o número de botões com frequência difere do número de vértices dos sólidos platônicos, não há bola cujos botões correspondem a 20 vértices do dodecaedro e a disposição dos botões não é sempre simétrica.[6]
Os antigos Gregos estudaram os sólidos platônicos extensivamente. Algumas fontes (tais como Proclo) creditam Pitágoras pela descoberta dos sólidos platônicos. Outra evidência sugere que ele pode ter sido apenas familiarizado com o tetraedro, o cubo e o dodecaedro e que a descoberta do octaedro e do icosaedro deve-se a Teeteto, contemporâneo de Platão. Em qualquer caso, Teeteto produziu uma descrição matemática de todos os cinco e, pode ter sido responsável pela primeira prova conhecida de que não existe nenhum outro poliedro regular convexo.
Os sólidos platônicos são destaque na filosofia de Platão. O filósofo escreveu sobre eles no diálogo Timeu, 360 a.C., no qual associou cada um dos quatro elementos clássicos (terra, ar, água e fogo) a um sólido regular. A terra foi associada com o cubo, o ar com o octaedro, a água com o icosaedro, e o fogo com o tetraedro. Havia uma justificativa intuitiva para estas associações. O calor do fogo parece afiado e agudo (como o pequeno tetraedro). O ar é feito do octaedro, pois seus minúsculos componentes são tão suaves que mal podem ser sentidos. À água associou o icosaedro, pois flui da mão quando apanhada, como se fosse feita de pequenas bolinhas. Por outro lado, um sólido não esférico, o hexaedro (cubo) representa a "terra". Além disso, por ser o único sólido regular que representa o espaço euclidiano, acreditava-se que o cubo fosse o que possibilitava solidez à Terra.
O quinto sólido platônico, o dodecaedro, Platão obscuramente observou, "...o deus usou [isto] para organizar as constelações no céu inteiro". Aristóteles acrescentou um quinto elemento, aithēr (aether em latim, "ether", em inglês ou éter em português) e postulou que foram feitos os céus com este elemento, mas ele não tinha interesse em definir correspondência com o quinto sólido de Platão.[7]
Euclides realizou uma descrição matemática dos sólidos platônicos na obra Elementos, sendo seu último livro (Livro XIII) destinado às suas propriedades. As proposições 13-17 do Livro XIII descrevem a construção do tetraedro, octaedro, cubo, icosaedro e dodecaedro nesta mesma ordem. Para cada sólido, Euclides encontrou a relação entre o diâmetro da esfera circunscrita e o comprimento da aresta. Na Proposição 18 ele argumentou o fato de não haverem mais poliedros regulares convexos. Andreas Speiser defendeu a ideia de que a construção dos cinco sólidos regulares era o objetivo principal do sistema dedutivo sustentado na obra Elementos.1 + √52 Muitas das informações do Livro XIII são provavelmente derivadas do trabalho de Teeteto.
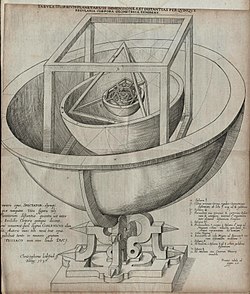
No século XVI o astrônomo alemão Johannes Kepler tentou relacionar os seis planetas conhecidos na época aos cinco sólidos platônicos. Em Mysterium Cosmographicum (O Mistério Cosmográfico), publicado em 1596, Kepler propôs um modelo do Sistema Solar no qual os cinco sólidos estavam inseridos dentro de um outro sólido, sendo separados entre si por uma série de esferas inscritas e circunscritas. Kepler propôs que as relações entre as distâncias dos seis planetas conhecidos na época poderiam ser entendidas em termos dos cinco sólidos platônicos contidos numa esfera que representava a órbita de Saturno. As seis esferas correspondiam a cada um dos planetas (Mercúrio, Vênus, Terra, Marte, Júpiter e Saturno). Os sólidos estavam ordenados com a mais profunda essência, sendo o octaedro, seguido pelo icosaedro, dodecaedro, tetraedro, e finalmente o cubo, ditando assim a estrutura do Sistema Solar e as relações de distância entre os planetas pelos sólidos platônicos. Ao final, a teoria original de Kepler foi abandonada, mas a partir de sua pesquisa originaram-se as três leis da dinâmica orbital, a primeira era de que as órbitas dos planetas são elipses ao invés de círculos, mudando o curso da física e da astronomia. Ele também descobriu os poliedros de Kepler-Poinsot.
No século XX, tentativas de associações entre os sólidos platônicos e o mundo físico entraram em expansão para o modelo de camada de elétrons na química, por Robert Moon em uma teoria conhecida como "Modelo da Lua".
Coordenadas cartesianas[editar | editar código-fonte]
Para os sólidos platônicos com centro na origem, as coordenadas cartesianas dos vértices são dadas abaixo. A letra grega φ é usada para representar a proporção áurea .
As coordenadas do tetraedro, do icosaedro e do dodecaedro são dadas em dois conjuntos de orientações, cada um contendo metade das permutações de sinal e posição das coordenadas.
Estas coordenadas revelam certas relações entre os sólidos platônicos: os vértices do tetraedro representam metade dos vértices do cubo, como {4,3}, um dos dois conjuntos de 4 vértices em posições duplas, como h{4,3}. Ambas posições tetraédricas geram o composto octaedro estrelado.
As coordenadas do icosaedro estão relacionadas a dois conjuntos alternados de coordenadas de um octaedro truncado não uniforme, t{3,4}, também visto no composto de dois icosaedros.
Oito dos vértices do dodecaedro são compartilhados com o cubo. Completando todas as orientações obtém-se o composto de cinco cubos.
Propriedades combinatórias[editar | editar código-fonte]
Um poliedro convexo é um sólido platônico se, e somente se,
- todas as suas faces são polígonos convexos regulares congruentes,
- nenhuma das faces se interseta, exceto nas arestas, e
- o mesmo número de faces se encontra em cada um dos seus vértices.
Cada sólido platônico pode ser denotado por um símbolo {p, q}, onde
- p é o número de arestas (ou, equivalentemente, vértices) de cada face, e
- q é o número de faces (ou, equivalentemente, arestas) que se encontram em cada vértice.
O símbolo {p, q}, chamado de símbolo de Schläfli, fornece uma descrição combinatória do poliedro. Os símbolos de Schläfli dos cinco sólidos platônicos são dados na tabela abaixo.
| Poliedro | Vértices | Arestas | Faces | Símbolo de Schläfli | Configuração dos Vértices | |
|---|---|---|---|---|---|---|
| tetraedro | 4 | 6 | 4 | {3, 3} | 3.3.3 | |
| cubo | 
|
8 | 12 | 6 | {4, 3} | 4.4.4 |
| octaedro | 
|
6 | 12 | 8 | {3, 4} | 3.3.3.3 |
| dodecaedro | 
|
20 | 30 | 12 | {5, 3} | 5.5.5 |
| icosaedro | 12 | 30 | 20 | {3, 5} | 3.3.3.3.3 | |
Todas as outras informações combinatórias sobre esses sólidos, como o número total de vértices (V), arestas (A) e faces (F), podem ser determinadas a partir de p e q. Como qualquer aresta une dois vértices e tem duas faces adjacentes, devemos ter:
A outra relação entre esses valores é dada pela Característica de Euler:
Isso pode ser provado de várias maneiras. Juntas, essas três relações determinam completamente V, A e F:
Trocando p e q, inverte-se F e V mantendo A inalterado.
Como uma configuração[editar | editar código-fonte]
Os elementos dos sólidos platônicos podem ser expressos em uma matriz de incidência ou matriz de configuração. Os elementos da diagonal representam o número de vértices, arestas e faces. Os elementos que não estão na diagonal representam o número de elementos da coluna que são incidentes no elemento da linha. Por exemplo, a linha superior mostra um vértice que tem q arestas e q faces incidentes e, a linha inferior mostra uma face que tem p vértices e p arestas. Já a linha intermediária mostra uma aresta que tem 2 vértices e 2 faces. Os sólidos platônicos duais tem suas matrizes de incidência rotacionadas em 180 graus um do outro.[8]
| {p,q} | Platonic configurations | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ordem do grupo:
g = 8pq/(4-(p-2)(q-2)) |
g=24 | g=48 | g=120 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Classificação[editar | editar código-fonte]
Um resultado clássico é o de que existem apenas cinco poliedros regulares convexos. Abaixo, seguem dois argumentos comuns que demonstram não existirem mais do que cinco poliedros platônicos.
Prova geométrica[editar | editar código-fonte]
O argumento geométrico expresso a seguir é muito semelhante ao dado por Euclides em os Elementos[9][10]:
- Cada vértice do sólido deve ser um vértice para, pelo menos, três faces.
- Em cada vértice do sólido, o total, entre as faces adjacentes, dos ângulos entre os seus respectivos lados adjacentes deve ser menor que 360°. O valor inferior a 360° é chamado de ângulo de defeito (ou deficiência angular).
- Os ângulos de todos os vértices de todas as faces de um sólido de Platão são congruentes e cada um dos ângulos dos vértices de cada face deve ser inferior a 360°/3 = 120°.
- Polígonos regulares formados por seis ou mais lados só têm ângulos iguais ou superiores à 120°, de modo que as únicas possibilidades de polígonos para as faces são ou o triângulo, ou o quadrado, ou o pentágono. Para esses diferentes tipos de faces, valem as seguintes relações:
- Faces triangulares: Cada ângulo do vértice de um triângulo equilátero (regular) tem 60°, de modo que o sólido pode ter 3, 4 ou 5 triângulos reunidos em cada vértice; os sólidos formados são o tetraedro, o octaedro e o icosaedro, respectivamente;
- Faces quadrangulares: Cada vértice de um quadrado tem 90°, de modo que é possível combinar apenas três faces em cada vértice do sólido, resultando no cubo;
- Faces pentagonais: Cada vértice tem 108° e apenas uma combinação de três faces em cada vértice é possível, resultando no dodecaedro.
- No total, é possível formar apenas cinco sólidos platônicos.
Prova topológica[editar | editar código-fonte]
Uma prova puramente topológica pode ser desenvolvida utilizando apenas informações sobre as propriedades combinatórias dos sólidos. A solução é obtida por meio da Característica de Euler que define que V - A + F = 2, e pelo fato de que pF = 2A = qV, onde p representa o número de arestas existentes em cada face e q representa o número de arestas que se encontram em cada vértice. Relacionando estas equações, é possível obter a seguinte equação
Com algumas manipulações algébricas, obtemos
Sabendo que A é um valor positivo, devemos ter
Usando o fato de que tanto p como q devem ter um valor mínimo igual a 3, pode-se notar que só existem cinco possibilidades para {p, q}:
- {3, 3}, {4, 3}, {3, 4}, {5, 3}, {3, 5}.
Propriedades geométricas[editar | editar código-fonte]
Ângulos[editar | editar código-fonte]
Há um número de ângulos associados a cada sólido de Platão. O ângulo diedro é o ângulo interior entre quaisquer duas faces planas. O ângulo diedro, θ, do sólido {p,q} é dado pela fórmula
Isso às vezes é mais convenientemente expresso em termos da tangente por
O valor de h (chamado de número de Coxeter) é igual a 4, 6, 6, 10 e 10 para o tetraedro, cubo, octaedro, dodecaedro e icosaedro, respectivamente.
O ângulo de defeito no vértice de um poliedro é a diferença entre a soma dos ângulos das faces de um vértice e 2π. O defeito, δ, em qualquer vértice de sólidos platônicos {p,q} é
Pelo teorema de Descartes, isto é igual a 4π dividido pelo número de vértices (i.e. o defeito total em todos os vértices é 4π).
O análogo tridimensional de um ângulo plano é um ângulo sólido. O ângulo sólido, Ω, no vértice de um sólido de Platão é dado em termos do ângulo diedro por
Isso decorre da fórmula do excesso esférico para um polígono esférico e do fato de que a figura do vértice do poliedro {p,q} é um q-gon (polígono com q arestas) regular.
O ângulo sólido de uma face subentendida a partir do centro de um sólido de Platão é igual ao ângulo sólido de uma esfera completa (4π esferorradianos) dividido pelo número de faces. Note que isto é igual à deficiência angular de seu dual.
Os diversos ângulos associadas com os sólidos platônicos estão tabelados abaixo. Os valores numéricos dos ângulos sólidos são dados em esferorradianos. A constante é a proporção áurea.
| Poliedro | Ângulo diedro(θ) | tan θ/2 | Defeito angular (δ) | Ângulo sólido do
vértice (Ω) |
Ângulo sólido da face |
|---|---|---|---|---|---|
| tetraedro | 70,53° | ||||
| cubo | 90° | ||||
| octaedro | 109,47° | ||||
| dodecaedro | 116,57° | ||||
| icosaedro | 138,19° |
Raios, área e volume[editar | editar código-fonte]
Outra virtude da regularidade é que todos os sólidos platônicos possuem três esferas concêntricas:
- a esfera circunscrita (circunsfera) que passa por todos os vértices;
- a meiasfera que é tangente ao ponto médio de cada aresta do poliedro; e
- a esfera inscrita (insfera) que é tangente a cada face exatamente em seu centro.
Os raios dessas esferas designam as distâncias do centro do poliedro para os vértices, para os pontos médios das arestas, e para o centro das faces, respectivamente. O raio R da circunsfera e o raio r da insfera do sólido {p, q} com comprimento da aresta igual a a são dadas por
onde θ é o ângulo diedro. O raio ρ da meiasfera é dado por
onde h é o valor utilizado anteriormente na definição do ângulo diedro (h = 4, 6, 6, 10, ou 10). Observe que a relação entre o raio da circunsfera para o raio da insfera é simétrico em p e q:
A área da superfície, A, de um sólido de Platão {p, q} é facilmente calculada como a área de um p-gon regular vezes o número de faces F. Isto é:
O volume é calculado como F vezes o volume da pirâmide cuja base é um p-gon regular e cuja altura é o raio r da insfera. Ou seja,
A tabela a seguir lista vários raios dos sólidos platônicos, juntamente com a sua área de superfície e volume. O tamanho total é fixado tomando o comprimento da aresta, a, como sendo igual a 2.
| Poliedro
(a = 2) |
Raio da insfera (r) | Raio da meiasfera (ρ) | Raio da circunsfera (R) | Área da superfície (A) | Volume (V) | Volume
(aresta unitária) |
|---|---|---|---|---|---|---|
| tetraedro | ||||||
| cubo | ||||||
| octaedro | ||||||
| dodecaedro | ||||||
| icosaedro |
As constantes φ e ξ acima, são dadas por
Entre os sólidos platônicos, ou o dodecaedro ou o icosaedro podem ser vistos como as melhores aproximações da esfera. O icosaedro tem o maior número de faces, além do maior ângulo diedro. Também possui maior estreitamento com a esfera inscrita e a relação entre a área de sua superfície e o volume é mais próxima à de uma esfera de mesmo tamanho (i.e. a mesma área da superfície ou o mesmo volume.) O dodecaedro, por outro lado, possui a menor deficiência angular, os vértices com maior ângulo sólido, e preenche melhor a sua esfera circunscrita.
Propriedade de Rupert[editar | editar código-fonte]
Diz-se que um poliedro P tem a propriedade de Rupert se um poliedro do mesmo ou maior tamanho e da mesma forma que P puder passar por um buraco em P.[11] Os cinco sólidos platônicos têm essa propriedade.[11][12][13]
Simetria[editar | editar código-fonte]
Poliedros duais[editar | editar código-fonte]
Cada poliedro possui um poliedro dual (ou "polar") com faces e vértices alternados. O dual de cada sólido de Platão é outro sólido de Platão, de modo que é possível organizar os cinco sólidos em pares duais.
- O tetraedro é auto-dual (i.e. seu dual é outro tetraedro);
- O cubo e o octaedro formam um par dual;
- O dodecaedro e o icosaedro formam um par dual.
Se um poliedro tem o símbolo de Schläfli igual a {p, q}, então seu dual tem o símbolo {q, p}. De fato, cada propriedade combinatória de um sólido de Platão pode ser interpretada como outra propriedade combinatória do dual.
Um poliedro dual pode ser construído tomando os centros das faces do poliedro original como sendo os vértices do novo poliedro. Ligando por segmentos de reta os centros das faces adjacentes do poliedro original, formam-se as arestas do dual e, assim, alterna-se o número de faces e vértices, mantendo o número de arestas.
De modo geral, pode-se dualizar um sólido de Platão com relação a uma esfera de raio d concêntrica ao sólido. O raio (R, ρ, r) de um sólido e os de seu dual (R*, ρ*, r*) estão relacionados por
Dualizar com relação à meiasfera (d = ρ) é muitas vezes conveniente, porque a meiasfera tem a mesma relação para ambos os poliedros. Levando d2 = Rr produz-se um sólido dual com o mesmo raio da circunsfera e da insfera (i.e. R* = R e r* = r).
Grupos de simetria[editar | editar código-fonte]
Na matemática, o conceito de simetria é estudado com a noção de grupos matemáticos. Cada poliedro está associado a um grupo de simetria, que é o conjunto de todas as transformações (isometrias euclidianas), que deixam o poliedro invariável. A ordem do grupo de simetria é o número de simetrias do poliedro. Muitas vezes existe diferença entre o número do grupo de simetria completo, o qual inclui reflexões, e o grupo de simetria próprio, que inclui apenas rotações.
Os grupos de simetria dos sólidos platônicos são uma classe especial de grupos de pontos tridimensionais conhecidos como grupos poliédricos. O alto grau de simetria dos sólidos platônicos pode ser interpretado de várias maneiras. Mais importante, os vértices de cada sólido são todos equivalentes sob a ação do grupo de simetria, assim como as arestas e faces. Uma define que a ação do grupo de simetria é transitiva sobre os vértices, arestas e faces. De fato, esta é uma outra forma de definir a regularidade de um poliedro: um poliedro é regular se, e somente se, ele possui vértices uniformes, arestas uniformes e faces uniformes.
Existem apenas três grupos de simetria associados com os sólidos platônicos, em vez de cinco, uma vez que o grupo de simetria de qualquer poliedro coincide com o de seu dual. Isso é facilmente verificado examinando a construção do poliedro dual. Qualquer simetria do original deve ser uma simetria do dual e vice-versa. Os três grupos poliédricos são:
- o grupo tetraédrico T;
- o grupo octaédrico O (que também é o grupo de simetria do cubo); e
- o grupo icosaédrico I (que também é o grupo de simetria do dodecaedro).
As ordens do grupo de simetria próprio (o qual inclui apenas rotações) são 12, 24 e 60, respectivamente - precisamente o dobro do número de arestas dos respectivos poliedros. As ordens dos grupos de simetria completo valem o dobro das do grupo de simetria próprio (ou seja, 24, 48 e 120). Todos os sólidos platônicos, com exceção do tetraedro, são centralmente simétricos, o que significa que são preservados sob reflexão através da origem.
A tabela a seguir lista as várias propriedades de simetria dos sólidos platônicos. Os grupos de simetria listados são os grupos completos com os subgrupos de rotação entre parênteses (o mesmo vale para o número de simetrias). A construção do caleidoscópio de Wythoff é um método para a construção direta de poliedros a partir de seus grupos de simetria. Eles estão listados em cada um dos sólidos platônicos para referência do símbolo de Wythoff.
| Poliedro | Símbolo de Schläfli | Símbolo de Wythoff |
Poliedro dual | Grupo de simetria (Reflexão, rotação) | ||||
|---|---|---|---|---|---|---|---|---|
| Grupo poliédrico | Notação de Schönflies | Notação de Coxeter | Notação de Orbifold | Ordem do grupo | ||||
| tetraedro | {3, 3} | 3 | 2 3 | tetraedro | Tetraédrico |
Td T |
[3,3] [3,3]+ |
*332 332 |
24 12 |
| cubo | {4, 3} | 3 | 2 4 | octaedro | Octaédrico |
Oh O |
[4,3] [4,3]+ |
*432 432 |
48 24 |
| octaedro | {3, 4} | 4 | 2 3 | cubo | |||||
| dodecaedro | {5, 3} | 3 | 2 5 | icosaedro | Icosaédrico |
Ih I |
[5,3] [5,3]+ |
*532 532 |
120 60 |
| icosaedro | {3, 5} | 5 | 2 3 | dodecaedro | |||||
Na natureza e tecnologia[editar | editar código-fonte]

O tetraedro, o cubo e o octaedro são encontrados naturalmente em estruturas cristalinas. Estes não esgotam o número de formas possíveis de cristais. No entanto, nem o icosaedro regular, nem o dodecaedro regular estão entre eles. Uma das formas, o chamado pyritohedron (nomeado para o grupo de minerais de que ele é típico) tem doze faces pentagonais, dispostas no mesmo padrão das faces do dodecaedro regular. As faces do pyritohedron, no entanto, não são regulares, de modo que o pyritohedron também não é regular. Alótropos do boro e muitos compostos do boro, tais como o carboneto de boro, contém discretos B12 icosaédricos em suas estruturas cristalinas. O ácido carborano também tem estruturas moleculares que se aproximam do icosaedro regular.
No início do século 20, Ernst Haeckel descreveu um número de espécies de Radiolaria, cujos esqueletos são em forma de vários poliedros regulares. Exemplos incluem Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus and Circorrhegma dodecahedra. As formas dessas criaturas devem ser óbvias a partir de seus nomes.
Muitos vírus, como o herpes, têm a forma de um icosaedro regular. Estruturas virais são construídas por repetição de subunidades de proteínas idênticas e o icosaedro é a forma mais fácil de montar usando estas subunidades. Um poliedro regular é usado porque ele pode ser construído a partir de uma única unidade básica de proteína utilizada repetidas vezes; isso economiza espaço no genoma do vírus.
Na meteorologia e na climatologia, modelos numéricos globais de fluxo atmosférico são de interesse crescente e empregam redes geodésicas baseadas em um icosaedro (refinado por triangulação) em vez da grade mais comumente usada longitude/latitude. Isto tem a vantagem de uma resolução espacial uniformemente distribuída sem singularidades (i.e. sem pólos), porém com dificuldade numérica aumentada.
A geometria em estruturas espaciais é, muitas vezes, baseada nos sólidos platônicos. No sistema MERO, os sólidos platônicos são utilizados para a convenção da nomenclatura de várias configurações de estruturas espaciais. Por exemplo, 12O+T refere-se a uma configuração composta pela metade de um octaedro e um tetraedro.
Vários hidrocarbonetos platônicos foram sintetizados, incluindo cubano e dodecaedrano.

Os sólidos platônicos são frequentemente usados para construir dados, porque os dados com estas formas são mais justos. Os dados de 6 lados são muito comuns, mas os outros números são comumente usados em jogos de RPG. Tais dados são comumente referidos como dn onde n é o número de faces (d8, d20, etc.).
Estas formas frequentemente aparecem em outros jogos ou quebra-cabeças. Quebra-cabeças similares ao de um Cubo de Rubik existem em todas as cinco formas.
Cristais líquidos com simetrias de sólidos platônicos[editar | editar código-fonte]
Para o estágio de material intermediário chamado cristais líquidos, a existência de tais simetrias foi proposta pela primeira vez em 1981 por H. Kleinert e K. Maki.[14][15] Em alumínio, a estrutura icosaédrica foi descoberta três anos após esta por Dan Shechtman, o que lhe valeu o Prêmio Nobel de Química em 2011.
Operações sobre sólidos platônicos[editar | editar código-fonte]
Poliedros duais[editar | editar código-fonte]

O poliedro dual de um sólido platônico é outro sólido platônico.
- O dual do tetraedro é um tetraedro
- O dual do octaedro é um cubo, e vice versa.
- O dual do dodecaedro é um icosaedro, e vice versa.
Truncatura[editar | editar código-fonte]
Truncando sólidos platônicos obtêm-se onze dos treze sólidos de Arquimedes:
O tetraedro truncado, o cuboctaedro, o cubo truncado, o octaedro truncado, o rombicuboctaedro, o cuboctaedro truncado, o icosidodecaedro, o dodecaedro truncado, o icosaedro truncado, o rombicosidodecaedro e o icosidodecaedro truncado.
Snubificação[editar | editar código-fonte]
Por snubificação de sólidos platônicos são obtidos dois sólidos de Arquimedes: o cubo snub e o dodecaedro snub.
Propriedades métricas dos sólidos platônicos[editar | editar código-fonte]
A tabela seguinte agrupa algumas das principais propriedades métricas dos sólidos platônicos.
Seja d a medida da aresta de um poliedro; podemos calcular em função de d os raios r, R, ρ, respectivamente da esfera inscrita, circunscrita e tangente à aresta. Também a área S da superfície e o volume V. Das fórmulas da tabela pode-se deduzir as relações inversas.
| Nome | r | R | ρ | S | V |
|---|---|---|---|---|---|
| Tetraedro | [3] | [3] | [16] | [16] | |
| Cubo ou Hexaedro regular | [3] | [3] | [3] | [3] | |
| Octaedro | [3] | [3] | [17] | [17] | |
| Dodecaedro | [18] | [18] | |||
| Icosaedro | [19] | [19] |
Notas[editar | editar código-fonte]
- ↑ Alguns autores definem os poliedros de Platão como poliedros convexos em que:
- todas as faces possuem o mesmo número de arestas;
- todos os ângulos poliédricos são formados pelo mesmo número de arestas;
- vale a relação de Euler V - A + F = 2 (onde V é o número de vértices, A é o número de arestas e F é o número de faces).
- todas as faces são polígonos regulares e congruentes, logo possuem o mesmo número de arestas;
- os ângulos poliédricos são congruentes, assim possuem o mesmo número de arestas em todos os vértices.
Referências[editar | editar código-fonte]
- ↑ Giovanni, José Ruy; Bonjorno, José Roberto; Giovanni Júnior, José Ruy (2002). Matemática Fundamental: uma nova abordagem. São Paulo: FTD
- ↑ James Elmes, A general and bibliographical dictionary of the fine arts (1824), Geometry, p.375 [google books]
- ↑ a b c d e f g h i Dolce, Osvaldo; Nicolau Pompeo, José (2013). Fundamentos da Matemática Elementar 7 ed. São Paulo: Atual
- ↑ Gardner (1987): Martin Gardner wrote a popular account of the five solids in his December 1958 Mathematical Games column in Scientific American.
- ↑ Plato's Timaeus
- ↑ Lloyd 2012.
- ↑ Wildberg (1988): Wildberg discusses the correspondence of the Platonic solids with elements in Timaeus but notes that this correspondence appears to have been forgotten in Epinomis, which he calls "a long step towards Aristotle's theory", and he points out that Aristotle's ether is above the other four elements rather than on an equal footing with them, making the correspondence less apposite.
- ↑ Coxeter, Regular Polytopes, sec 1.8 Configurations
- ↑ Mello, Leila Inês Pagliarini; Rheinheimer, Juliana Mercedes (2015). «Por que apenas 5 poliedros de Platão?». Revista Eletrônica da Matemática. Consultado em 24 de agosto de 2018
- ↑ Demski Martins, Thatielle; Goldoni, Viviane. «Descobrindo os Poliedros de Platão» (PDF)
- ↑ a b Jerrard, Richard P.; Wetzel, John E.; Yuan, Liping (abril de 2017). «Platonic Passages». Washington, DC: Mathematical Association of America. Mathematics Magazine. 90 (2): 87-98. doi:10.4169/math.mag.90.2.87
- ↑ Schrek, D. J. E. (1950), «Prince Rupert's problem and its extension by Pieter Nieuwland», Scripta Mathematica, 16: 73–80 and 261–267
- ↑ Scriba, Christoph J. (1968), «Das Problem des Prinzen Ruprecht von der Pfalz», Praxis der Mathematik (em alemão), 10 (9): 241–246, MR 0497615
- ↑ Kleinert and Maki (1981)
- ↑ The liquid-crystalline blue phases (1989). by Tamar Seideman, Reports on Progress in Physics, Volume 53, Number 6
- ↑ a b Marcelo Rigonatto. «Tetraedro regular». Mundo Educação. Consultado em 21 de junho de 2018
- ↑ a b Marcos Noé Pedro da Silva. «Octaedro regular». Mundo Educação. Consultado em 30 de agosto de 2018
- ↑ a b Marcos Noé Pedro da Silva. «Dodecaedro». Mundo Educação. Consultado em 21 de junho de 2018
- ↑ a b Marcos Noé Pedro da Silva. «Icosaedro Regular». Mundo Educação. Consultado em 21 de junho de 2018