PageRank

PageRank™ é um algoritmo utilizado pela ferramenta de busca Google para posicionar websites entre os resultados de suas buscas. O PageRank mede a importância de uma página contabilizando a quantidade e qualidade de links apontando para ela. Não é o único algoritmo utilizado pelo Google para classificar páginas da internet, mas é o primeiro utilizado pela companhia e o mais conhecido.
Suas propriedades são muito discutidas por especialistas em optimização dos motores de busca (SEO, sigla em inglês para Search Engine Optimization).
O processo do PageRank foi patenteado pela Universidade de Stanford nos Estados Unidos sob o número 6.285.999.[1] Somente o nome PageRank é uma marca registrada do Google.
O Google tem os direitos de licença exclusivos sobre a patente de PageRank. A Universidade de Stanford recebeu 1,8 milhão de ações do Google em troca do uso da patente. As ações foram vendidas em 2005 por 336 milhões de dólares.[2]
Descrição[editar | editar código-fonte]
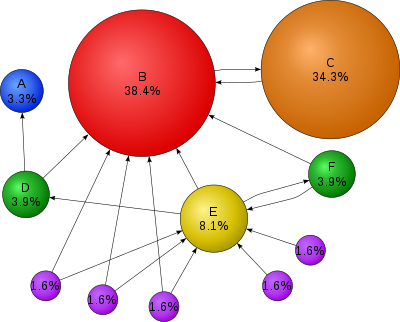
Na construção da métrica de PageRank, a web é vista como uma rede de citações, cada nó corresponde a uma página e cada ligação corresponde a uma referência de uma página para outra (hiperligação). A métrica atribui um valor a cada nó (página) da rede, um valor maior corresponde a um nó mais importante na rede. Do ponto de vista da teoria das redes, PageRank é uma métrica de centralidade. Esta métrica tira partido da estrutura de hiperligações na web para produzir o valor para cada página da rede. Uma hiperligação a uma página conta como um “voto” de suporte. O valor de PageRank de uma página depende do número de páginas e da métrica PageRank[3] dessas páginas que aponta para si. Uma página tem um valor mais alto de PageRank se:
- existem muitas página a apontar para si
- existem algumas páginas a apontar para si com uma métrica de PageRank alta (uma página é importante se páginas importantes apontarem para si)
Google e o PageRank[editar | editar código-fonte]
O sistema PageRank é usado pelo motor de busca Google para ajudar a determinar a relevância ou importância de uma página. Foi desenvolvida pelos fundadores do Google, Larry Page e Sergey Brin enquanto cursavam a Universidade de Stanford em 1998.
O Google mantém uma lista de bilhões de páginas em ordem de importância, isto é, cada página tem sua importância na Web como um todo; esse Banco de Páginas mantém desde a página mais importante do mundo até a menos importante. Essa importância se dá pelo número de votos que uma página recebe. Um voto é um link em qualquer lugar da Web para aquela página. Votos de páginas mais importantes valem mais do que votos de páginas menos importantes.
Esse critério de ordenação das páginas, de acordo com várias pessoas, é bastante democrático, reflectindo o que a "Web pensa" sobre determinado termo. Lembre-se que cerca de dez bilhões de páginas são levadas em conta. A qualidade das páginas mais importantes são naturalmente garantidas, classificadas e eleitas pela própria Web. Além de todas as páginas terem a mesma condição de subir nessa lista, conquistando votos pela Web afora.
Uma boa unidade de medida para definir o PageRank de uma página pode ser a percentagem (%) de páginas sobre as quais sua importância se sobreleva. Por exemplo, se uma página tem PageRank de 33% significa que ela é mais importante que um terço de toda a Web. Se o seu PageRank é 99% significa que ela é superior a quase todas as páginas da Web.
No entanto, é possível manipular o PageRank atribuindo links descontextualizados com o objectivo da página, modificando a ordenação de resultados na pesquisa pelo Google e induzindo a resultados pouco relevantes ou tendenciosos. Um exemplo recente disso é a pesquisa por failure ou miserable failure que retornava como primeiro site a biografia oficial da Casa Branca para o presidente dos Estados Unidos, George W. Bush e em sequência a página de Michael Moore, inimigo declarado do presidente dos EUA. Este processo ficou conhecido por Googlebombing. Apesar disso, o Google tem removido alguns resultados decorrentes de "Googlebombing".
  |
|
|
História[editar | editar código-fonte]
PageRank foi desenvolvido na Universidade de Stanford por Larry Page (daí o nome Page Rank [4] ) e Sergey Brin em 1996, [5] no contexto de um projeto de investigação sobre um novo tipo de motor de busca.[6][7] Sergey Brin teve a ideia de que a informação na web poderiam ser ordenada numa hierarquia de "popularidade de ligações": Uma página é mais importante se tiver mais hiperligações a apontar para si. Foi co-autoria de Rajeev Motwani e Terry Winograd. O primeiro artigo sobre o projeto, descrevendo a métrica PageRank e o protótipo inicial do motor de busca Google, foi publicado em 1998.[6] Logo depois, Page e Brin fundaram a Google Inc., a empresa por trás do motor de busca Google.
A métrica PageRank foi inspirada na análise de citações, desenvolvida por Eugene Garfield em 1950 na Universidade da Pensilvânia, e pelo método “Hyper Search”, desenvolvido por Massimo Marchiori, da Universidade de Pádua. No mesmo ano, foi introduzido o PageRank (1998), Jon Kleinberg publicou seu trabalho sobre HITS. Os fundadores do Google citaram Marchiori, e Kleinberg no seu artigo original.[6]
Um motor de busca chamado "RankDex" da IDD Information Services, desenhado por Robin Li, desde 1996, já explorava uma estratégia semelhante para pontuação e ranking de páginas [8]. A tecnologia utilizada em RankDex foi patenteada em 1999 [9] e usada mais tarde quando Li fundou a Baidu na China.[10][11] O trabalho de Li está referenciado em algumas patentes, de métodos de pesquisa do Google, de Larry Page.[12]
O algoritmo[editar | editar código-fonte]
A métrica PageRank de uma página representa a probabilidade de uma pessoa chegar a essa página, clicando aleatoriamente em hiperligações. O cálculo de PageRank é escalável, ou seja, é executável em tempo útil se aumentarmos consideravelmente o número de páginas da rede. O cálculo de PageRank é iterativo, ou seja, exige várias passagens, chamadas de "iterações", os valores obtidos em cada iteração convergem para os valores desejados de PageRank. Na primeira iteração é atribuído um valor de PageRank inicial igual para todas as páginas (N é o número total de páginas).
O algoritmo simplificado[editar | editar código-fonte]
Imagine uma rede de apenas 4 páginas A, B, C e D. As ligações de uma página a si própria e as ligações múltiplas entre duas páginas são ignoradas.
Inicialmente, a soma dos valores de PageRank de todas as páginas da web correspondia ao número de páginas na web. Em versões posteriores, o PageRank, passou a assumir valores entre 0 e 1, representando uma distribuição probabilística, ou seja, a probabilidade de um utilizador, percorrendo ligações aleatoriamente, chegue a uma determinada página.
No primeiro passo do processo de cálculo iterativo do PageRank, todas as páginas têm o mesmo valor de PageRank. No nosso exemplo de 4 páginas, o primeiro passo consiste em atribuir o valor 0,25 de PageRank a cada uma das quatro páginas. Note-se que a soma dos valores de PageRank de todas as páginas é 1.
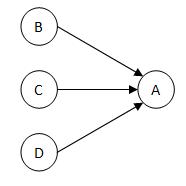
Numa rede com a configuração da figura em cima, na segunda iteração, cada ligação transfere o valor 0,25 para o PageRank de A, ou seja:

No caso da rede em cima, na segunda iteração, o valor de B é transferido metade para A (0,125) e outra metade para C (0,125). Como D referencia 3 páginas, o seu valor a transferir é dividido por três, neste caso o PageRank de A recebe os seguintes valores.
Portanto, a contribuição de uma ligação para o PageRank da página referenciada, é igual ao valor de PageRank da página com a ligação, dividido pelo número de ligações que a página contém. Se representarmos por L() o número de ligações de uma página, podemos reescrever a expressão em cima, para a nossa rede de 4 páginas:
Generalizando, o valor de PageRank para uma página u pode ser expresso da seguinte forma:
O valor de PageRank de uma página u, depende dos valores de PageRank de cada página v contida no conjunto Bu (conjunto de todas as páginas que referenciam u), dividido pelo número de referências L(v) existentes em v.
Páginas sem ligações[editar | editar código-fonte]
O processo iterativo de cálculo de PageRank encontra problemas quando uma página não tem ligação a outras páginas.

Se for aplicado o cálculo à rede da figura anterior, acabamos por obter o valor zero para ambas as páginas A e B [13] . Em cada iteração, B recebe algum do PageRank de A (neste caso particular B recebe todo o PageRank de A, mas numa rede mais complexa onde A tivesse ligações a outras páginas, B receberia apenas uma parte do PageRank), mas como B não tem ligações, não passa o seu valor a outras páginas, neste caso A. Isto produz um efeito de drenagem do PageRank para fora da rede.
Ciclo (rank sink)[editar | editar código-fonte]
Outro problema encontrado no cálculo do PageRank acontece quando uma rede contém um ciclo (rank sink).
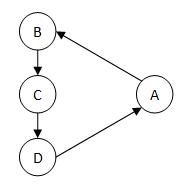
Considere-se um ciclo fechado de páginas ligadas entre si, mas que nenhuma das páginas ligue a uma página fora do ciclo. Num cenário destes, o cálculo do PageRank fica "preso" no ciclo infinito, em cada iteração o valor de PageRank é transmitido de uma página para outra do ciclo, sem nunca distribuir o valor para páginas fora do ciclo [13] e sem que os valores convirjam para valores estacionários de PageRank.
Fator de amortecimento[editar | editar código-fonte]
Os problemas acima descritos são resolvidos por um conceito introduzido pelo PageRank e designado por fator de amortecimento. A teoria de PageRank considera que um utilizador (ou surfista) imaginário que siga as ligações entre as páginas, aleatoriamente, acabará por se aborrecer e parar de seguir as ligações. A probabilidade, em cada passo, de o utilizador continuar a seguir as ligações é o fator de amortecimento d. O fator de amortecimento, sendo uma probabilidade, pode variar entre 0 e 1.
Desta forma o valor de PR(A) passa a ter uma componente correspondente à contribuição das páginas que apontam para A, ponderado pela probabilidade d do utilizador seguir as ligações das páginas:
e uma componente correspondente ao utilizador ter selecionada a página aleatoriamente ponderado pela probabilidade de o utilizador não seguir as ligações das páginas (1-d)
Com a introdução do fator de amortecimento d, o cálculo do valor de PageRank, passa a ter a seguinte expressão, representa o número total de páginas:
Existem outras variantes para o cálculo de PageRank, mas a expressão em cima tem a particularidade de a soma dos valores de PageRank de todas as páginas ser 1. Obtém-se desta forma uma distribuição probabilística, ou seja, a probabilidade de um utilizador chegar à página A.
O fator de amortecimento introduz as seguintes características no cálculo de PageRank:
- Uma página, pelo simples facto de existir, tem uma probabilidade igual a todas as outras de ser selecionada pela escolha aleatória de um utilizador
- Uma página que não tenha ligações está ligada a todas as páginas da rede
- Resolução dos problemas de páginas sem ligações e ciclos (rank sink).
O fator de amortecimento d pode assumir valores entre zero e 1, como já foi indicado. Com d = 1, passamos à forma simplificada do algoritmo, com d = 0, não é atribuído nenhum peso à estrutura de hiperligações entre páginas da rede, todas as páginas ficam com o valor de PageRank igual a , onde é o número de páginas da rede. Portanto, quanto mais próximo estiver d de 1, maior é o peso dado á estrutura da rede. É normalmente atribuído o valor 0,85 para o fator de amortecimento [6].
Representação matricial[editar | editar código-fonte]
Assumindo que a rede é constituída pelas páginas P1, P2, …, Pn, M(Pi) representa o conjunto de páginas que referenciam Pi, L(Pj) representa o número de referências na página Pj. A expressão para o cálculo do valor de PageRank, pode ser reescrito da seguinte forma:
- (*)
O vetor R que contém o valor de PageRank para todas das páginas pode ser representado da seguinte forma
Construindo uma matriz de transição M de nxn, onde n é o número total de páginas, um elemento Mij (linha i e coluna j) é dado pela função :
- , se não existe referência da página pj para a página pi
- , se existe referência da página pj para a página pi, : é o número de referências existentes em pj (grau de saída ou número de ligações que saem de pj)
- Note-se que a função está normalizada, ou seja :
A expressão para o cálculo de PageRank para todas as páginas, pode ser escrita da seguinte forma matricial:
Se representarmos por 1 o vector de uns, com o valor 1 em todos os elementos, com n linhas e uma coluna, temos:
- .
Um vez que a soma de todos os elementos do vetor R é 1 (ou seja PR(P1)+PR(P2)+…PR(Pn) = 1 ), então o produto de R pela matriz E nxn, com o valor 1 em todos os seus elementos, é igual ao vetor 1, Portanto, podemos reescrever a expressão para o cálculo de R, da seguinte forma:
Colocando R em evidência, obtemos:
Ou seja, R é o vetor próprio da matriz de adjacências modificada , para o valor próprio 1, onde:
Portanto, a métrica PageRank pode ser vista como uma variante da métrica de centralidade de vetor próprio.
Cálculo iterativo da métrica PageRank[editar | editar código-fonte]
Vamos designar por x(0) os valores iniciais de PageRank e por x(t) os valores calculados de PageRank na iteração t.
Na primeira iteração t=0, é atribuído o valor a todas as páginas, ou seja, cada elemento do vetor x(0) tem o valor:
Em cada iteração t+1, calculamos o valor de x(t+1) multiplicando a matriz pelo vetor x(t) ( valores de PageRank calculados na iteração anterior):
A matriz tem as seguintes propriedades[13]:
- irredutível
- primitiva
- estocástica
Com base nestas propriedades de , prova-se[13] que x(t) converge para o vetor próprio R [14].
O cálculo iterativo termina quando a variação de x(t) para x(t+1), é menor que um determinado valor pré-definido:
Esta forma de cálculo é escalável, numa rede com 322 milhões de ligações, verifica-se uma convergência, com uma tolerância razoável, em aproximadamente 52 iterações [7]. A velocidade de convergência, neste método de cálculo depende do valor de amortecimento d [15].
Determinar o PageRank[editar | editar código-fonte]
Para verificar o PageRank de uma determinada página deve-se visitar sites que fornecem a cotação do site
Nofollow e o PageRank[editar | editar código-fonte]
A partir de 2010 o Google começou a utilizar a tag: rel:nofollow como um critério a mais ao PageRank. Anteriormente, quando era verificada essa tag nas páginas o Google as ignorava. Essa ação do Google era devido ao fato de serem considerados spams as páginas quem continham essa tag. O propósito em ignorar essas páginas estava relacionado ao fato de nas pesquisas aparecerem páginas irrelevantes, ou seja, imprecisão no resultado de busca. Posteriormente, com a difusão do linkjuice, o Google modificou o julgamento quanto em relação ao nofollow. Quando é encontrado um linkjuice, este é ignorado e à página não é acrescentada a votação no PageRank.
Referências
- ↑ «Patent Public Search | USPTO». ppubs.uspto.gov. Consultado em 16 de janeiro de 2023
- ↑ «Stanford Earns $336 Million Off Google Stock». Redorbit (em inglês). 1 de dezembro de 2005. Consultado em 16 de janeiro de 2023
- ↑ «O que é Pagerank - Conheça todos os segredos e o que é Pagerank». Centro do Saber. 16 de fevereiro de 2017
- ↑ David Vise and Mark Malseed (2005). The Google Story. [S.l.: s.n.] p. 37. ISBN ISBN 0-553-80457-X Verifique
|isbn=(ajuda) - ↑ Raphael Phan Chung Wei (16 de maio de 2002). «New Straits Times» Computimes; 2 ed.
- ↑ a b c d The Anatomy of a Large-Scale Hypertextual Web Search Engine, Computer Networks and ISDN Systems, Volume 30, Issues 1–7, Brin, S.; Page, L., April 1998, Pages 107–117, Proceedings of the Seventh International World Wide Web Conference
- ↑ a b Page, Lawrence; Brin, Sergey; Motwani, Rajeev and Winograd, Terry (1998), The PageRank Citation Ranking: Bringing Order to the Web, Technical Report, Stanford University
- ↑ Li, Yanhong (6 de Agosto de 2002). "Toward a qualitative search engine". Internet Computing, IEEE (IEEE Computer Society) 2 (4): 24–29.
- ↑ "Hypertext Document Retrieval System and Method", Patente Nº U.S.: 5920859, Criador: Yanhong Li, Filing Data: 5 de Fevereiro de 1997, Data emissão: 6 de Julho de 1999
- ↑ Greenberg, Andy, "The Man Who's Beating Google", Forbes magazine, 5 de Outubro de 2009
- ↑ "About: RankDex", rankdex.com
- ↑ specially Lawrence Page, Patentes: 6,799,176 (2004) "Method for scoring documents in a linked database", 7,058,628 (2006) "Method for node ranking in a linked database", and 7,269,587 (2007) "Scoring documents in a linked database"2011
- ↑ a b c d David Austin Grand Valley State University, "How Google Finds Your Needle in the Web's Haystack",The American Mathematical Society
- ↑ Altman, Alon; Moshe Tennenholtz (2005). "Ranking Systems: The PageRank Axioms". Proceedings of the 6th ACM conference on Electronic commerce (EC-05). Vancouver, BC. Retrieved 2008-02-05
- ↑
Taher Haveliwala and Sepandar Kamvar. (2003). «The Second Eigenvalue of the Google Matrix» (PDF). Stanford University Technical Report: 7056. Bibcode:2003math......7056N. arXiv:math/0307056
 [math.FA]
[math.FA]



























