Função hiperbólica

	Trigonometria
	História ; Funções; Funções inversas ; Aprofundamento ;
	Referência
	Lista de identidades ; CORDIC
	Teoria euclidiana
	Lei dos senos ; Lei dos cossenos ; Lei das tangentes ; Teorema de Pitágoras
	Cálculo
	Integração trigonométrica ; Substituição trigonométrica ; Integrais de funções ; Diferenciação trigonométrica ; ;

Na matemática, funções hiperbólicas são funções análogas às funções trigonométricas ordinárias, estas também conhecidas como funções circulares. Funções hiperbólicas foram introduzidas por volta de 1760 de maneira independente pelos matemáticos Vincenzo Riccati e Johann Heinrich Lambert^[1]. As funções hiperbólicas básicas são o seno hiperbólico e o cosseno hiperbólico, dos quais são derivados a tangente hiperbólica, a cossecante hiperbólica ou a secante hiperbólica e a cotangente hiperbólica, análogas às funções trigonométricas derivadas. Em alguns casos, suas inversas também são consideradas funções hiperbólicas.

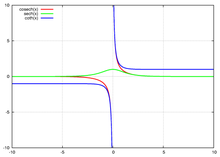
Essa classe de funções recebe esse nome porque, em muitos casos nos quais o uso de funções trigonométricas gera círculos ou elipses, o uso de funções hiperbólicas gera hipérboles, como, por exemplo, no caso das equações paramétricas:

x=\cos t\,

y=\sin t\,

Estas geram um círculo, enquanto que as equações:

x=\cosh t\,

y=\sinh t\,

geram (uma metade de) uma hipérbole.

Funções hiperbólicas aparecem nas soluções de várias equações diferenciais lineares, nas soluções de algumas equações cúbicas, em cálculos de ângulos e distâncias na geometria hiperbólica e em cálculos da Equação de Laplace em coordenadas cartesianas. Equações de Laplace são importantes em diversas áreas da física, incluindo eletromagnetismo, transferência de calor, hidrodinâmica e relatividade restrita.

Na análise complexa, as funções hiperbólicas surgem como as partes imaginárias das funções trigonométricas seno e cosseno. Quando são consideradas como definidas por uma variável complexa, as funções hiperbólicas são funções racionais de exponenciais e, portanto, holomórficas.

Expressões padrão das funções hiperbólicas

As expressões das funções hiperbólicas são as seguintes:

Seno hiperbólico:

$\sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}={\frac {1-e^{-2x}}{2e^{-x}}}$

Cosseno hiperbólico:

$\cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}={\frac {1+e^{-2x}}{2e^{-x}}}$ .

Tangente hiperbólica:

$\tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$

$={\frac {e^{2x}-1}{e^{2x}+1}}={\frac {1-e^{-2x}}{1+e^{-2x}}}$

Cotangente hiperbólica: $x\not =0$

$\coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}=$

$={\frac {e^{2x}+1}{e^{2x}-1}}={\frac {1+e^{-2x}}{1-e^{-2x}}}$

Secante hiperbólica:

$\operatorname {sech} \,x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}$

$={\frac {2e^{x}}{e^{2x}+1}}={\frac {2e^{-x}}{1+e^{-2x}}}$

Cossecante hiperbólica: $x\not =0$

$\operatorname {csch} \,x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}$

$={\frac {2e^{x}}{e^{2x}-1}}={\frac {2e^{-x}}{1-e^{-2x}}}$

Derivadas das funções hiperbólicas

As derivadas das funções hiperbólicas são as seguintes:

Derivada do seno hiperbólico:

${\frac {d}{dx}}\sinh x=\cosh x$

Derivada do cosseno hiperbólico:

${\frac {d}{dx}}\cosh x=\sinh x$

Derivada da tangente hiperbólica:

${\frac {d}{dx}}\tanh x=1-\tanh ^{2}x=\operatorname {sech} ^{2}x=1/\cosh ^{2}x$

Derivada da cotangente hiperbólica:

${\frac {d}{dx}}\coth x=1-\coth ^{2}x=-\operatorname {csch} ^{2}x=-1/\sinh ^{2}x$ , se $x\not =0$

Derivada da secante hiperbólica:

${\frac {d}{dx}}\ \operatorname {sech} \,x=-\tanh x\ \operatorname {sech}$

Derivada da cossecante hiperbólica:

${\frac {d}{dx}}\ \operatorname {csch} \,x=-\coth x\ \operatorname {csch}$ , se $x\not =0$

Derivadas das funções hiperbólicas inversas

Ver artigo principal: Função hiperbólica inversa

As derivadas das funções hiperbólicas inversas (também chamadas de funções arco) são as seguintes:

Derivada do arco seno hiperbólico:

${\frac {d}{dx}}\,\operatorname {arsinh} \,x={\frac {1}{\sqrt {x^{2}+1}}}$

Derivada do arco cosseno hiperbólico:

${\frac {d}{dx}}\,\operatorname {arcosh} \,x={\frac {1}{\sqrt {x^{2}-1}}}$ , se $1<x$

Derivada do arco tangente hiperbólico:

${\frac {d}{dx}}\,\operatorname {artanh} \,x={\frac {1}{1-x^{2}}}$ , se $-1<x<1$

Derivada do arco cotangente hiperbólico:

${\frac {d}{dx}}\,\operatorname {arcoth} \,x={\frac {1}{1-x^{2}}}$ , se $\left\vert x\right\vert >1$

Derivada do arco secante hiperbólico:

${\frac {d}{dx}}\,\operatorname {arsech} \,x=-{\frac {1}{x{\sqrt {1-x^{2}}}}}$ , se $0<x<1$

Derivada do arco cossecante hiperbólico:

${\frac {d}{dx}}\,\operatorname {arcsch} \,x=-{\frac {1}{|x|{\sqrt {1+x^{2}}}}}$ , se $x\not =0$

Relações com as funções trigonométricas

As funções hiperbólicas podem ser definidas, usando-se números complexos, a partir das funções trigonométricas:

$\sin(ix)=i\sinh x\,$
$\cos(ix)=\cosh x\,$
$\tan(ix)=i\tanh x\,$
$\cos(x)=\cosh(ix)$
$\sin(x)=i\sinh(-ix)$
$\tan(x)=i\tanh(-ix)\,$

onde i é uma unidade imaginária com a propriedade i² = −1.

As formas complexas nas definições acima são provenientes da Fórmula de Euler.

Prova resumida de $\cos(ix)=\cosh(x)$ :

$\cos(xy)=e^{xyi}{\frac {1}{2}}+e^{-xyi}{\frac {1}{2}}$ :

$\cos(ix)=e^{-x}{\frac {1}{2}}+e^{x}{\frac {1}{2}}=\cosh(x)$

O mesmo funciona para as demais relações afirmadas.

Relações importantes (para t real)

$(\operatorname {senh} (t)+\cosh(t))^{m}=(e^{t})^{m}=e^{mt}=\operatorname {senh} (mt)+\cosh(mt)$

$e^{2t}=\left({\frac {\sinh(t)+\cosh(t)}{\cosh(t)-\sinh(t)}}\right)$

$e^{2t}=(\sinh(t)+\cosh(t))^{2}$

$\cosh ^{2}(t)-\operatorname {senh} ^{2}(t)=1$

$e^{-t}(\sinh(t)+\cosh(t))=1$

$e^{t}(\sinh(t)-\cosh(t))=-1$

Referências

↑ Robert E. Bradley, Lawrence A. D'Antonio, Charles Edward Sandifer. Euler at 300: an appreciation. Mathematical Association of America, 2007. Página 100.

- GRAVILLE SMITH, William Elementos de Cálculo Diferencial e Integral Editora Biblioteca da Marinha do Brasil, 1950.

Ligações Externas

Hazewinkel, Michiel, ed. (2001), «Hyperbolic functions», Enciclopédia de Matemática, ISBN 978-1-55608-010-4 (em inglês), Springer (em inglês)
Hyperbolic functions on PlanetMath (em inglês)
Hyperbolic functions entry at MathWorld (em inglês)
Web-based calculator of hyperbolic functions (em inglês)

Ver também

Catenária, o gráfico da função $y=\cosh x\,$ .

[1] Robert E. Bradley, Lawrence A. D'Antonio, Charles Edward Sandifer. Euler at 300: an appreciation. Mathematical Association of America, 2007. Página 100.

[1]