Usuário(a):WilsonNeuroMat/Testes72

Em matemática, uma série é o somatório dos termos de uma sequência de números.

Dada uma sequência infinita $(a_{1},a_{2},a_{3},\dots )$, a $n$-ésima soma parcial $S_{n}$ é a soma dos primeiros termos da sequência, isto é,

$S_{n}=\sum _{k=1}^{n}a_{k}.$

Uma série é convergente se a sequência de suas somas parciais $\{S_{1},S_{2},S_{3},\dots \}$ tende a um limite. Isto quer dizer que as somas parciais se tornam cada vez mais próximas de um dado número quando o número de seus termos aumenta. Mais precisamente, uma série converge se existir um número $\ell$ tal que, para qualquer número $\varepsilon$ positivo arbitrariamente pequeno, há um número inteiro $N$ (suficientemente grande), tal que para todo $n\geq N$, Em uma linguagem mais formal, uma série converge se existe um limite $\ell$ tal que para qualquer número positivo arbitrariamente pequeno $\varepsilon >0$, existe um inteiro $N$ tal que para todo $n\geq \ N$,

$|S_{n}-\ell |\leq \varepsilon .$

Qualquer série que não é convergente é chamada de divergente.

Exemplos de séries convergentes e divergentes

• Os inversos dos inteiros positivos produzem uma série divergente (série harmônica):

  ${1 \over 1}+{1 \over 2}+{1 \over 3}+{1 \over 4}+{1 \over 5}+{1 \over 6}+\cdots \rightarrow \infty .$

• Alternar os sinais dos inversos dos inteiros positivos produz uma série convergente:

  ${1 \over 1}-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}-{1 \over 6}+\cdots =\ln 2.$

• Alternar os sinais dos inversos dos inteiros ímpares produz uma série convergente (a Fórmula de Leibniz para $\pi$):

  ${1 \over 1}-{1 \over 3}+{1 \over 5}-{1 \over 7}+{1 \over 9}-{1 \over 11}+\cdots ={\pi \over 4}.$

• Os inversos dos números primos produzem uma série divergente (assim sendo, o conjunto dos primos é "grande"):

  ${1 \over 2}+{1 \over 3}+{1 \over 5}+{1 \over 7}+{1 \over 11}+{1 \over 13}+\cdots \rightarrow \infty .$

• Os inversos dos números triangulares produzem uma série convergente:

  ${1 \over 1}+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+{1 \over 21}+\cdots =2.$

• Os inversos dos fatoriais produzem uma série convergente (ver número de Euler $e$):

  ${\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+{\frac {1}{120}}+\cdots =e.$

• Os inversos dos números quadrados produzem uma série convergente (o Problema de Basileia):

  ${1 \over 1}+{1 \over 4}+{1 \over 9}+{1 \over 16}+{1 \over 25}+{1 \over 36}+\cdots ={\pi ^{2} \over 6}.$

• Os inversos das potências de 2 produzem uma série convergente (assim sendo, o conjunto das potências de 2 é "pequeno"):

  ${1 \over 1}+{1 \over 2}+{1 \over 4}+{1 \over 8}+{1 \over 16}+{1 \over 32}+\cdots =2.$

• Os inversos das potências de qualquer $n$ produzem uma série convergente:

  ${1 \over 1}+{1 \over n}+{1 \over n^{2}}+{1 \over n^{3}}+{1 \over n^{4}}+{1 \over n^{5}}+\cdots ={n \over n-1}.$

• Alternar os sinais dos inversos das potências de 2 também produz uma série convergente:

  ${1 \over 1}-{1 \over 2}+{1 \over 4}-{1 \over 8}+{1 \over 16}-{1 \over 32}+\cdots ={2 \over 3}.$

• Alternar os sinais dos inversos das potências de qualquer $n$ produz uma série convergente:

  ${1 \over 1}-{1 \over n}+{1 \over n^{2}}-{1 \over n^{3}}+{1 \over n^{4}}-{1 \over n^{5}}+\cdots ={n \over n+1}.$

• Os inversos dos números de Fibonacci produzem uma série convergente, sendo $\psi$ a constante dos inversos de Fibonacci:

  ${1 \over 1}-{1 \over 1}+{1 \over 2}-{1 \over 3}+{1 \over 5}-{1 \over 8}+\cdots =\psi .$

Testes de convergência

Se for possível provar que a série azul $\Sigma b_{n}$ converge, então a série menor $\Sigma a_{n}$ deve convergir. Por contraposição, se for possível provar que a série vermelha $\Sigma a_{n}$ diverge, então $\Sigma b_{n}$ também deve divergir.

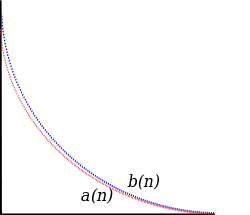
Existem alguns métodos para determinar se uma série converge ou diverge.

• Teste da comparação: Os termos da sequência $\left\{a_{n}\right\}$ são comparados àqueles de outra sequência $\left\{b_{n}\right\}$. Se,

para todo $n$, $0\leq a_{n}\leq b_{n}$ e $\sum _{n=1}^{\infty }b_{n}$ converge, então o mesmo acontece com $\sum _{n=1}^{\infty }a_{n}.$ Contudo, se, para todo $n$, $0\leq b_{n}\leq a_{n}$ e $\sum _{n=1}^{\infty }b_{n}$ diverge, então o mesmo acontece com $\sum _{n=1}^{\infty }a_{n}.$

• Teste da razão: Assuma que para todo $n$, $a_{n}>0$. Suponha que existe $r$ tal que:

  $\lim _{n\to \infty }{\frac {a_{n+1}}{a_{n}}}=r.$

Se $r<1$, então a série converge. Se $r>1$, então a série diverge. Se $r=1$, o teste da razão é inconclusivo e a série pode convergir ou divergir.

• Teste da raiz ou teste da raiz $n$-ésima: Suponha que os termos da sequência em questão são números não negativos. Defina $r$ como se segue:

  $r=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},$

em que $\limsup$ denota o limite superior (possivelmente $\infty$; se o limite existir, é o mesmo valor).

Se $r<1$, então a série converge. Se $r>1$, então a série diverge. Se $r=1$, o teste da raiz é inconclusivo e a série pode convergir ou divergir.

O teste da razão e o teste da raiz são ambos baseados na comparação com uma série geométrica e, como tal, funcionam em situações similares. De fato, se o teste da razão funcionar (significando que o limite existe e não é igual a 1), então o mesmo acontece com o teste da raiz. O inverso, porém, não é verdadeiro. Por isso, o teste da raiz é de aplicação mais geral, mas, em termos práticos, é frequentemente difícil computar o limite para tipos de séries comumente encontrados.

• Teste da integral: A série pode ser comparada com uma integral para estabelecer convergência ou divergência. Considere $f(n)=a_{n}$ uma função positiva e monotonicamente decrescente. Se

  $\int _{1}^{\infty }f(x)dx=\lim _{t\to \infty }\int _{1}^{t}f(x)dx<\infty ,$

então a série converge. No entanto, se a integral diverge, o mesmo acontece com a série.

• Teste da comparação do limite: Se $\{a_{n}\},\{b_{n}\}>0$, o limite $\lim _{n\to \infty }{\frac {a_{n}}{b_{n}}}$ existir e for diferente de zero, então $\sum _{n=1}^{\infty }a_{n}$ converge se e somente se $\sum _{n=1}^{\infty }b_{n}$ convergir.

• Teste da série alternada: Também conhecido como critério de Leibniz, o teste da série alternada estabelece que para uma série alternada da forma $\sum _{n=1}^{\infty }a_{n}(-1)^{n}$, se $\{a_{n}\}$ for monotonicamente decrescente e tiver um limite zero no infinito, então a série converge.

• Teste da condensação de Cauchy: Se $\{a_{n}\}$ for uma sequência monotonicamente decrescente positiva, então $\sum _{n=1}^{\infty }a_{n}$ converge se e somente se $\sum _{k=1}^{\infty }2^{k}a_{2^{k}}$ convergir.

Outros exemplos incluem o teste de Dirichlet, o teste de Abel e o teste de Raabe.

Convergência condicional e absoluta

Ilustração da convergência condicional da série de potência de $\log(z+1)$ em torno de 0 avaliado em $z=\exp((\pi -{\frac {1}{3}})i)$. O comprimento da linha é infinito.

Para qualquer sequência $\{a_{1},a_{2},a_{3},\dots \}$, $a_{n}\leq |a_{n}|$ para todo $n$. Por isso,

$\sum _{n=1}^{\infty }a_{n}\leq \sum _{n=1}^{\infty }|a_{n}|.$

Isto significa que, se $\sum _{n=1}^{\infty }|a_{n}|$ convergir, então $\sum _{n=1}^{\infty }a_{n}$ também converge (mas não vice-versa).

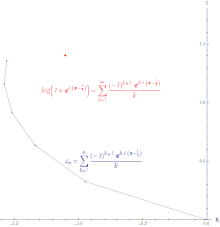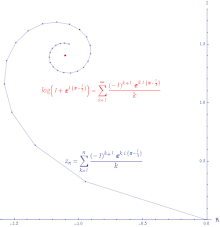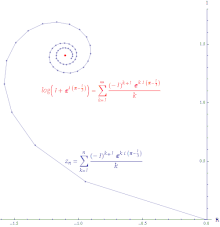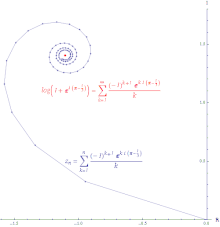
Se a série $\sum _{n=1}^{\infty }|a_{n}|$ convergir, então, a série $\sum _{n=1}^{\infty }a_{n}$ é absolutamente convergente. Um sequência absolutamente convergente é uma sequência na qual a linha criada ao juntar todos os incrementos à soma parcial é finitamente longa. A série das potências da função exponencial é absolutamente convergente em todo lugar.

Se a série $\sum _{n=1}^{\infty }a_{n}$ convergir, mas a série $\sum _{n=1}^{\infty }|a_{n}|$ divergir, então a série $\sum _{n=1}^{\infty }a_{n}$ é condicionalmente convergente. O caminho formado ao conectar as somas parciais de uma série condicionalmente convergente é infinitamente longo. A série das potências do logaritmo é condicionalmente convergente.

O teorema das séries de Riemann afirma que, se uma série convergir condicionalmente, é possível rearranjar os termos da série de tal maneira que a série converge a qualquer valor ou até mesmo diverge.

Convergência uniforme

Ver artigo principal: Convergência uniforme

Considere $\{f_{1},f_{2},f_{3},\dots \}$ uma sequência de funções. Diz-se que a série $\sum _{n=1}^{\infty }f_{n}$ converge uniformemente a $f$ se a sequência $\{s_{n}\}$ de somas parciais definida por:

$s_{n}(x)=\sum _{k=1}^{n}f_{k}(x)$

convergir uniformemente a $f$.

Há um análogo do teste de comparação para séries infinitas de funções chamado teste M de Weierstrass.

Critério de convergência de Cauchy

O critério de convergência de Cauchy afirma que uma série $\sum _{n=1}^{\infty }a_{n}$ converge se e apenas se a sequência de somas parciais for uma sequência de Cauchy.

Isto significa que, para todo $\varepsilon >0$, há um número inteiro positivo $N$ tal que, para $n\geq m\geq N$, temos:

$\left|\sum _{k=m}^{n}a_{k}\right|<\varepsilon ,$

que é equivalente a:

$\lim _{n\to \infty \atop m\to \infty }\sum _{k=n}^{n+m}a_{k}=0.$

Ver também

• Limite de uma sequência
• Série divergente