Usuário:Gildemar Felix/Distribuição de probabilidade

Em teoria da probabilidade e em estatística, uma distribuição de probabilidade descreve o comportamento aleatório de um fenômeno dependente do acaso. O estudo dos fenômenos aleatórios começou com o estudo dos jogos de azar. Jogos de dados, sorteios de bolas de uma urna et jeu de pile ou face ont été eram motivações para compreender e prever os experimentos aleatórios. Essas abordagens iniciais são fenômenos discretos, ou seja, o número de resultados possíveis é finito ou contável. Entretanto, certas questões ont cependant fait apparaître des lois à support infinito não contável — por exemplo, quando a realização do jogo de cara ou coroa tende ao infinito, o número de coroas obtidos aproxima—se de uma distribuição normal.

Flutuações e variabilidade estão presentes em quase todo valor que pode ser medido durante a observação de um fenômeno, independente de sua natureza, de plus presque toutes les mesures ont une part d'erreur intrinsèque. A distribuição de probabilidade pode modelar incertezas e descrever fenômenos físicos, biológicos, econômicos. O domínio da estatística permite de trouver des lois de probabilités adaptées aux phénomènes aléatoires.

Représentation de trois fonctions de répartition de lois de probabilité :

• en rouge, celle d'une loi absolument continue, la loi normale centrée réduite ;
• en bleu, celle d'une loi discrète, la loi de Poisson de paramètre 2 ;
• en noir, celle d'une loi mixte, combinaison linéaire d'une mesure de Dirac en -2, d'une mesure de Dirac en -1 et d'une loi de Cauchy de paramètres -2 et 1.

Há muitas distribuições de probabilidade diferentes. Entre as distribuições de probabilidade, a distribuição normal tem uma importância particular. De acordo com o teorema central do limite, a distribuição normal aborda o comportamento assintótico de várias distribuições de probabilidade.

O conceito de distribuição de probabilidade é formalizado matematicamente pela teoria da medida: uma distribuição de probabilidade é uma medida muitas vezes vista como uma distribuição que descreve o comportamento de uma variável aleatória discreta ou contínua. Uma medida é uma distribuição de probabilidade se sua massa total for 1. O estudo de uma variável aleatória de acordo com uma distribuição de probabilidade discreta fait apparaître des calculs de sommes et de séries, alors que si sa loi est absolument continue, l'étude de la variable aléatoire fait apparaître des calculs d'intégrales. As funções particulares permitem caracterizar as distribuições de probabilidade — por exemplo, a função de distribuição e a função característica.

Definição informal

Uma descrição de probabilidade descreve teoricamente a característica aleatória de uma experiência considerada aleatória. O conceito de experiência aleatória surgiu para descrever um processo real de natureza experimental, em que o acaso intervém com resultados possíveis bem identificados — por exemplo, em um lançamento de um dado (um evento aleatório) os resultados podem ser um número entre 1 e 6 com igual probabilidade (a distribuição de probabilidade afirma que há a mesma chance de sairem os seis resultados com probabilidade de um sexto).

Historicamente distribuições de probabilidade foram estudados em jogos de azar, jogos de dados, jogos de cartas. Se os resultados possíveis dos fenômenos forem números contáveis, a distribuição de probabilidade é chamada discreta. CONTRÁRIO. Donner la loi de probabilité revient à donner la liste des valeurs possibles avec leurs probabilités associées. Elle est alors donnée sous forme de formule, de tableau de valeurs, d'arbre de probabilité ou de fonctions (qui seront détaillées dans les sections suivantes).

Em um contexto mais amplo, se os números dos resultados possíveis de um fenômeno aleatório forem finitos (contáveis ou incontáveis) em vez de infinitos, a distribuição de probabilidade sempre descreve a distribuição de probabilidade dos resultados possíveis, mas caracterizados como funções (funções densidade, funções distribuição, entre outros) ou mais geralmente por medidas.

Histórico

Ver artigo principal: História da teoria das probabilidades

La planche de Galton, imaginée en 1889, permet de visualiser la courbe de Gauss comme loi limite.

O uso do acaso existe desde os tempos antigos, especialmente em jogos de azar, em apostas de riscos de transportes marítimos ou em rendas vitalícias. Entretanto uma das primeiras referências conhecidas para os cálculos de probabilidade é um cálculo elementar sobre a Divina Comédia, que aparece apenas no século XV durante o Renascimento. Os primeiros tratados forment o início da teoria da probabilidade, principalmente com base em probabilidades combinatórias. Os problemas se posent ainsi, à propos de la durée de um jogo de cartas:

“ Sur la durée des parties que l'on joue en rabattant. On demande combien il y a à parier que la partie qui peut durer à l'infini sera finie en un certain nombre déterminé de coups au plus. ”

—  Pierre Rémond de Montmort, em seu livro Essay d'analyse sur les jeux de hazard.

Reconhece—se a probabilidade (a aposta) de uma variável (a duração de um jogo) ser menor que um valor (um certo número determinado), que representa a função de distribuição da distribuição de probabilidade de um jogo.

Esta é a tese de Nicolau Bernoulli, publicada em 1711, em que aparece pela primeira vez a distribuição uniforme. Outras distribuições font alors leur apparition como a distribuição binomial e a distribuição normal, embora suas abordagens não sejam completamente rigorosas— por exemplo, a distribuição normal foi desenvolvida por Abraham de Moivre com uma curva de Gauss por uma aproximação numérica. No século XVIII, outras ideias de distribuições de probabilidade emergiram com a expectativa de uma variável aleatória discreta com Jean le Rond D'Alembert ou de probabilidades condicionais com Thomas Bayes. Algumas distribuições de probabilidade contínuas estão contidas em uma memória de Joseph—Louis Lagrange, de 1770.

O uso rigoroso das distribuições de probabilidade começou a partir do século XIX, nas ciências aplicadas como na biometria com Karl Pearson ou na física estatística com Ludwing Boltzmann.

A definição formal das medidas de probabilidade surgiu em 1896 com uma publicação de Émile Borel, continuando com outros matemáticos como Henri—Léon Lebesgue, Maurice René Fréchet, Paul Lévy e principalmente Andrei Kolmogorov que formulou os axiomas de probabilidade em 1933.

Definição matemática

Em teoria da probabilidade, uma distribuição de probabilidade é uma medida com massa total igual a 1. Essa medida satisfaz os três axiomas de probabilidade.

Definição — Para um espaço mensurável $\scriptstyle (\Omega ,{\mathcal {A}})$, $\scriptstyle \mathbb {P}$ é uma distribuição de probabilidade, medida de probabilidade ou simplesmente probabilidade se:

1. $\scriptstyle \mathbb {P}$ é uma aplicação de $\scriptstyle {\mathcal {A}}$ dans [0,1];
2. $\scriptstyle \mathbb {P} (\Omega )=1$;
3. $\scriptstyle \mathbb {P}$ é $\scriptstyle \sigma$—aditiva. Isto é, para qualquer família finita ou contável de elementos disjuntos $\scriptstyle (A_{i},i\in I)$ de $\scriptstyle {\mathcal {A}}$;

$\mathbb {P} \left(\bigcup _{i\in I}A_{i}\right)=\sum _{i\in I}\mathbb {P} (A_{i}).$ Uma consequência imediata é: $\scriptstyle \mathbb {P} (\emptyset )=0$.

O triplet $\scriptstyle (\Omega ,{\mathcal {A}},\mathbb {P} )$ é chamado de espaço de probabilidade. Uma maneira usual de expressão de uma distribuição é o uso de uma variável aleatória porque para qualquer distribuição de probabilidade $\scriptstyle \mathbb {P}$ de $\scriptstyle (\Omega ,{\mathcal {A}})$ existe uma variável aleatória $\scriptstyle X$ definida em um espaço de probabilidade (potencialmente diferente de $\scriptstyle (\Omega ,{\mathcal {A}})$) e de distribuição $\scriptstyle \mathbb {P}$. Entre as distribuições mais estudadas em teoria da probabilidade, estão as distribuições de valores reais que podem ser representadas por uma variável aleatória real.

Definição — Seja uma variável aleatória real no espaço de probabilidade$\scriptstyle \ (\Omega ,{\mathcal {A}},\mathbb {P} )$. Isto é, uma função mensurável $\scriptstyle X:(\Omega ,{\mathcal {A}})\rightarrow (\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))$. A distribuição de probabilidade da variável aleatória $\scriptstyle X$ é a medida de probabilidade $\scriptstyle \mathbb {P} _{X}$, definida sobre o espaço mensurável $\scriptstyle (\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))$ por $\mathbb {P} _{X}(B)=\mathbb {P} {\big (}X^{-1}(B){\big )}=\mathbb {P} (X\in B),$para qualquer álgebra de Borel real $\scriptstyle B\in {\mathcal {B}}(\mathbb {R} )$. Em outras palavras, $\scriptstyle \mathbb {P} _{X}$ é a mesure image de $\scriptstyle \mathbb {P}$ para $\scriptstyle X$.

Então, para definir a distribuição de uma variável aleatória, transpõe—se a distribuição de probabilidade $\scriptstyle \mathbb {P}$ de $\scriptstyle \Omega$ em uma medida $\scriptstyle \mathbb {P} _{X}$ de $\scriptstyle \mathbb {R}$.

A representação de uma distribuição por uma variável aleatória não é única. Em outras palavras, duas variáveis aleatórias diferentes ou duas variáveis aleatórias definidas em espaços diferentes podem ter a mesma distribuição. Duas variáveis aleatórias reais $\scriptstyle X$ e $\scriptstyle Y$ tem a mesma distribuição $\scriptstyle \mathbb {P} _{X}=\mathbb {P} _{Y}\$(em termos de igualdade de medidas). Isto é, $\scriptstyle \mathbb {P} _{X}(B)=\mathbb {P} _{Y}(B)$, pata todo $\scriptstyle B\in {\mathcal {B}}(\mathbb {R} )$. O seguinte teorema permite uma caracterização adicional.

Teorema de transferência ou de transporte — Seja uma variável aleatória real $\scriptstyle X:\Omega \rightarrow \mathbb {R}$. Logo $\mathbb {E} \left[\varphi (X)\right]{\stackrel {\text{déf.}}{=}}\int _{\Omega }\varphi {\big (}X(\omega ){\big )}\mathbb {P} (\mathrm {d} \omega )=\int _{\mathbb {R} }\varphi (x)\mathbb {P} _{X}(\mathrm {d} x),$ para toda função $\scriptstyle \varphi :\mathbb {R} \rightarrow \mathbb {R}$, de tal modo que pelo menos uma das duas integrais ait un sens.

L'intégrale apparaissant dans le dernier terme est l'intégrale, au sens de la théorie de la mesure, de la fonction $\scriptstyle \varphi$ par rapport à la mesure $\scriptstyle \mathbb {P} _{X}$. Esta integral tem forma de soma, no caso das distribuições discretas. Então, duas variáveis aleatórias reais $\scriptstyle X$ e $\scriptstyle Y$ tem a mesma distribuição $\scriptstyle \mathbb {E} \left[\varphi (X)\right]=\mathbb {E} \left[\varphi (Y)\right]$ para toda função $\scriptstyle \varphi :\mathbb {R} \rightarrow \mathbb {R}$, tal que pelo menos um dos dois termos da igualdade ait un sens.

Distribuição multidimensional

Loi normale bidimensionnelle, ou produit de deux lois normales unidimensionnelles.

Intuitivamente, uma distribuição de probabilidade é chamada de multidimensional ou n—dimensional quando descreve vários valores (aleatórios) de um fenômeno aleatório — por exemplo, no lançamento de dois dados, a distribuição de probabilidade dos dois resultados é uma distribuição bidimensional. Então, a característica multidimensional aparece por meio da transferência por uma variável aleatória de um espaço de probabilidade $\scriptstyle (\Omega ,{\mathcal {A}})$ para um espaço numérico $\scriptstyle E^{n}$, de dimensão n — por exemplo, no lançamento de dois dados, a dimensão é n = 2 e o espaço $\scriptstyle E^{2}$ é $\scriptstyle \{1,\dots ,6\}\times \{1,\dots ,6\}$. A distribuição também é chamada de distribuição conjunta.

Um exemplo importante da distribuição multidimensional é a loi de probabilité produit $\scriptstyle \mathbb {P} =\mathbb {P} _{1}\otimes \mathbb {P} _{2}$, em que $\scriptstyle \mathbb {P} _{1}$ e $\scriptstyle \mathbb {P} _{2}$ são duas distribuições unidimensionais. Essa distribuição de probabilidade é uma distribuição de um par de variáveis aleatórias independentes.Esse é o caso do exemplo do lançamento de dois dados.

Definição — Seja uma variável aleatória $\scriptstyle X$ no espaço de probabilidade $\scriptstyle (\Omega ,{\mathcal {A}},\mathbb {P} )$, com valores em $\scriptstyle {\mathbb {R} }^{n}$muni de la tribu borélienne réelle produit $\scriptstyle {{\mathcal {B}}(\mathbb {R} )}^{\otimes n}$. A distribuição da variável aleatória$\scriptstyle \ X\$é a medida de probabilidade $\scriptstyle \mathbb {P} _{X}$ definida para todo $\scriptstyle B\in {{\mathcal {B}}(\mathbb {R} )}^{\otimes n}$: $\mathbb {P} _{X}(B)=\mathbb {P} {\big (}X^{-1}(B){\big )}=\mathbb {P} (X\in B).$

A variável aleatória $\scriptstyle X$ é identificada a um vetor aleatório de dimensões n: $\scriptstyle X=(X_{1},X_{2},\dots ,X_{n})$.O teorema de Cramer—Wold estabelece que a distribuição (n—dimensional) do vetor aleatório é completamente determinado pelas distribuições (unidimensionais) de todas as combinações lineares dos componentes: $\scriptstyle \sum _{i=1}^{n}a_{i}X_{i}$ para todo $\scriptstyle a_{1},a_{2},\dots ,a_{n}$.

Distribuição absolutamente contínua

Les deux coordonnées (dimension 1 et dimension 2) des points s'approchent chacune d'une loi normale. C'est-à-dire qu'il s'agit d'une simulation de loi bidimensionnelle dont les deux lois marginales sont normales.

Uma distribuição bidimensional ou n—dimensional é chamada de absolutamente contínua em $\scriptstyle \mathbb {R} ^{2}$ se a distribuição é absolutamente contínua par rapport à la medida de Lebesgue em $\scriptstyle \mathbb {R} ^{2}$. Isto é, se a distribuição da variável aleatória correspondente é escrita na forma $\mathbb {P} (X\in B)=\iint _{B}f_{X}(x_{1},x_{2})\mathrm {d} x_{1}\mathrm {d} x_{2}$ para todo $\scriptstyle B\in {\mathcal {B}}(\mathbb {R} ^{2}).$

Distribuição marginal

Ver artigo principal: Distribuição marginal

Intuitivamente, a distribuição marginal de um vetor aleatório é a distribuição aleatória dos seus componentes. Para obter—la, projeta—se a distribuição em um espaço unidimensional de uma coordenada desejada. A distribuição de probabilidade da i—ésima coordenada de um vetor aleatório é chamado de i—ésima distribuição marginal. A distribuição marginal $\scriptstyle \mathbb {P} _{i}$ de $\scriptstyle \mathbb {P}$ é obtida pela fórmula:$\mathbb {P} _{i}(A)=\mathbb {P} _{X_{i}}(A)=\iint {1}_{\omega _{i}\in A}\mathbb {P} (\mathrm {d} (\omega _{1},\dots ,\omega _{n}))$ para todo $\scriptstyle A\in {\mathcal {B}}(\mathbb {R} )$. As distribuições marginais de uma distribuição absolutamente contínua são expressas com suas densidades marginais.

Distribuição condicional

Ver artigo principal: Probabilidade condicionada

Exemple d'utilisation d'une loi conditionnelle : + signifie que l'individu est positif au test de drogue ; U signifie que l'individu est consommateur de drogue. Ainsi $\mathbb {P} (+|U)$ est la probabilité que le test soit positif sur un individu consommateur de drogue.

Intuitivamente, uma distribuição de probabilidade condicionada permite descrever o comportamento de um fenômeno aleatório quando a informação sobre o processo é conhecida. Em outras palavras, a probabilidade condicionada permite avaliar o grau de dependência estocástica entre dois eventos — por exemplo, no lançamento de dois dados, a distribuição condicional pode dar a soma dos resultados sabendo que o resultado do lançamento de um dos dois dados foi pelo menos quatro.

Definição para eventos

A probabilidade condicionada é definida em eventos pela probabilidade $\scriptstyle \mathbb {P} (\cdot |B)$ de um evento A condicionado a um evento B para todo A e B da σ-álgebra subjacente tal como $\scriptstyle \mathbb {P} (B)\neq 0$: $\mathbb {P} (A|B)={\frac {\mathbb {P} (A\cap B)}{\mathbb {P} (B)}}.$

A distribuição de probabilidade $\scriptstyle \mathbb {P} (\cdot |B)$ é usada em probabilidade e em estatística elementares para a distribuição da probabilidade total ou o teorema de Bayes, por exemplo.

Definição para variáveis aleatórias

A probabilidade condicionada também é definida para as variáveis aleatórias. Seja uma variável X condicionada a uma variável Y. Quando $\scriptstyle \mathbb {P} (Y=y)\neq 0$, a distribuição de X dado Y = y é definida por $\mathbb {P} (X\in A|Y=y)={\frac {\mathbb {P} (X\in A,Y=y)}{\mathbb {P} (Y=y)}}.$

A definição acima não é válida se a distribuição de Y for absolutamente contínua dado que $\mathbb {P} (Y=y)=0$ para todo y. A definição seguinte é válida para quaisquer das duas variáveis aleatórias.

Definição — Seja $(X,Y)$ um par de variáveis aleatórias reais. Há uma distribuição de probabilidade $\mathbb {P} _{X|Y}$, chamada de distribuição condicional de $X$ dado $Y$ ou dado $Y=y$ definida pela e para qualquer função borélienne bornée $\varphi$: $\mathbb {E} \left[\varphi (X)|Y\right]=\int \varphi (x)\mathbb {P} _{X|Y}(\mathrm {d} x)$ quase certamente.

A distribuição também é denotada ${\mathcal {L}}(X|Y)$ ou ${\mathcal {L}}(X|Y=y)$. A igualdade anterior é uma igualdade entre variáveis aleatórias.

Definição para σ—álgebra

De maneira mais geral, a distribuição de probabilidade é definida a partir da esperança condicional de uma variável aleatória X dada uma σ-álgebra ${\mathcal {G}}$. Essa esperança condicional é a única variável aleatória ${\mathcal {G}}$—mensurável, denotada como $\mathbb {E} \left[X|{\mathcal {G}}\right]$ e satisfazendo: $\mathbb {E} \left[Z\mathbb {E} (X|{\mathcal {G}})\right]=\mathbb {E} \left[ZX\right]$ para todo Z, variável ${\mathcal {G}}$—mensurável. Então, a distribuição condicional é definida por $\mathbb {P} (A|{\mathcal {G}})=\mathbb {E} (1_{A}|{\mathcal {G}})$, em que $1_{A}$ é a função indicadora.

Definição para distribuições absolutamente contínuas

No caso das distribuições absolutamente contínuas, existe uma função densidade condicional de uma distribuição par rapport à l'autre, et inversement. Se $(x,y)\mapsto f(x,y)$ é a densidade da distribuição bidimensional, as duas densidades condicionais são dadas por

$f(x|y)={\frac {f(x,y)}{f_{Y}(y)}}={\frac {f(x,y)}{\int f(x,y)\mathrm {d} x}}$ e $f(y|x)={\frac {f(x,y)}{f_{X}(x)}}={\frac {f(x,y)}{\int f(x,y)\mathrm {d} y}}$.

$f_{X}$ e $f_{Y}$ são as duas distribuições marginais e X e Y, respectivamente. Quando as integrais são substituídas por somas, são obtidas fórmulas semelhantes quando as distribuições marginais serem discretas ou quando a distribuição marginal de X é discreta e de Y é absolutamente contínua ou vice—versa.

Distribuição com valores em um espaço de Banach

Quando $\scriptstyle \mathbb {R}$ é um espaço de Banach, as distribuições dos valores em um espaço de Banach são generalizações das distribuições dos valores reais. A definição é semelhante.

Définition — Seja uma variável aleatória em um espaço de probabilidade$\scriptstyle \ (\Omega ,{\mathcal {A}},\,\mathbb {P} )$ com valores em um espaço de Banach $\scriptstyle E$ com σ—álgebra $\scriptstyle {\mathcal {B}}$ gerada pelos conjuntos abertos de $\scriptstyle E$. A distribuição de probabilidade da variável aleatória$\scriptstyle \ X\$e a medida de probabilidade $\scriptstyle \mathbb {P} _{X}\$definida pelo espaço mensurável$\ (E,{\mathcal {B}})$ por$\mathbb {P} _{X}(B)=\mathbb {P} \left(X^{-1}(B)\right)=\mathbb {P} \left(X\in B\right),$ para todo $\scriptstyle B\in {\mathcal {B}}$.

Para obter bonnes propriedades, é comum considerar as medidas de probabilidade tensas. Isto é, intuitivamente concentradas em seu espaço compacto et de supposer que o espaço de Banach é separável.

Um possível exemplo do espaço de Banach é o espaço das funções contínuas $\scriptstyle {\mathcal {C}}(\mathbb {R} ^{+},\mathbb {R} )$. Um processo estocástico de uma família de variáveis aleatórias $\scriptstyle (X_{t})_{t\in T}$ indexadas por conjunto de índices T. Uma definição possível da distribuição de probabilidade de tal processo é chamada de distribuição finita—dimensional. Isto é, a distribuição multidimensional dos vetores $\scriptstyle (X_{t_{1}},X_{t_{2}},\dots ,X_{t_{n}})$quando $\scriptstyle t_{1},t_{2},\dots ,t_{n}\in T$. Então, a distribuição pode ser estendida pelo teorema da extensão de Carathéodory para todo o processo.É o exemplo do movimento browniano $\scriptstyle (B_{t})_{t\in \mathbb {R} _{+}}$(trajetórias contínuas), cuja distribuição de probabilidade é a medida de Weiner geralmente denotada por $W(A)=\mathbb {P} ((B_{t})_{t\geq 0}\in A)$, para todo subconjunto A de $\scriptstyle {\mathcal {C}}(\mathbb {R} ^{+},\mathbb {R} )$.

Espaço de distribuições de probabilidade

Uma distribuição de probabilidade é uma medida de massa total unitária. O conjunto de duas distribuições de probabilidade é um subespaço do espaço de medidas finitas. Esse espaço é muitas vezes denominado $\scriptstyle {\mathcal {P}}(\mathbb {R} )$ ou $\scriptstyle {\mathcal {M}}_{1}(\mathbb {R} )$ pelas distribuições de probabilidade reais. No restante da seção, as propriedades desse espaço são detalhadas para as distribuições de probabilidade reais. Elles sont cependant vraies sur les espaces de Banach.

É possível fornecer esse espaço com uma topologia chamada topologia fraca. Essa topologia define uma convergência fraca das distribuições de probabilidade: uma sequência de distribuições de probabilidade $\scriptstyle (\mathbb {P} _{n},n=1,2,\dots )$ converge fracamente para uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ se $\lim _{n\rightarrow \infty }\int \varphi (\omega )\mathbb {P} _{n}(\mathrm {d} \omega )=\int \varphi (\omega )\mathbb {P} (\mathrm {d} \omega )$ para toda função contínua $\varphi$ de um conjunto limitado.

A convergência é denominada $\scriptstyle \mathbb {P} _{n}{\xrightarrow {w}}\mathbb {P}$. Essa convergência é refletida pelo teorema de transferências de variáveis aleatórias $\scriptstyle (\mathbb {X} _{n},n=1,2\dots )$ dsa respectivas distribuições $\scriptstyle (\mathbb {P} _{n},n=1,2,\dots )$. Então, a convergência de variáveis aleatórias é chamada é denotada $\scriptstyle X_{n}{\xrightarrow {\mathcal {L}}}X$ ou $\scriptstyle X_{n}{\xrightarrow {\mathcal {D}}}X$. Se a convergência fraca das variáveis aleatórias é frequentemente utilizada, elle ne concerne en fait que leur loi.

O espaço de distribuições de probabilidade com topologia fraca é um espaço métrico, completo e separável (no caso de um espaço de Banach também separável), tornando—se um espace polonais.

Aspectos de Distribuições de Probabilidade

Podemos denominar a distribuição de probabilidade de $X$ como uma reunião de pares $(x_{i},p(x_{i}))$, onde $i=1,2,3,...$. Portanto, uma distribuição de probabilidade de uma variável aleatória discreta $X$, definida em um espaço amostral $\Omega$, é uma reta que associa cada valor de $X$ a sua probabilidade. Logo, a triple $\scriptstyle (R,B(\mathbb {R} ),P_{X})$ é uma distribuição de probabilidade, onde $P_{X}$ é a distribuição de variável aleatória. Por outro lado temos que o espaço amostral $\Omega$ possui uma probabilidade $P$ a qual se relaciona ao contra-domínio $\mathbb {R}$. Portanto, $\scriptstyle (\Omega ,\theta ,P)$, onde $P$ é a probabilidade.

Propriedades

Parâmetros e famílias

Certas distribuições são agrupadas por família par rapport à certaines propriedades da sua densidade ou da sua função massa ou suivant o número de parâmetros que as definem, chamados de família paramétrica de distribuição de probabilidade.

Différents paramètres de forme (asymétrie) pour la densité de probabilité de la Loi normale asymétrique.

Parâmetros

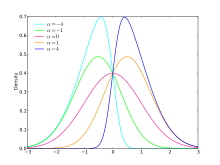
Os chamados parâmetros de posição influenciam a tendência central da distribuição de probabilidade. Isto é, la ou les valeurs autour desquelles la loi prend ses plus grandes valeurs — por exemplo, a esperança, a mediana, a moda ou diferentes quantils e decils.

Différents paramètres de position ($\scriptstyle \mu$) et paramètres d'échelle ($\scriptstyle \sigma$) pour la densité de probabilité de la loi normale.

Os chamados parâmetros de escalonamento influenciam a dispersão ou o achatamento da distribuição de probabilidade — por exemplo, a variância (momento de segunda ordem), o desvio padrão ou a amplitude interquartil.

Os chamados parâmetros de forma são outros parâmetros relacionados a distribuição de probabilidade. A cauda ou traîne de uma distribuição de probabilidade real faz parte de sua forma. As caudas da esquerda e da direita são dos tipos $\scriptstyle ]-\infty ,x[$ e $\scriptstyle [y,+\infty [$, respectivamente. Um distribuição de probabilidade é dita cauda pesada se a medida de probabilidade da cauda $\scriptstyle \mathbb {P} ([y,+\infty [)$ tend moins vite vers 0, pour x allant à l'infini, que celle de la distribuição normal. Especialmente toda distribuição absolutamente contínua — centrada — éduite dont la densité vérifie:

$\lim _{|x|\rightarrow +\infty }f(x)\exp \left({\frac {1}{2}}x^{2}\right)=+\infty$ é uma distribuição com caudas pesadas à direita e à esquerda.

A assimetria (momento de terceira ordem) é um exemplo de parâmetro de forma, que permite tornar a cauda da direita mais ou menos pesada. A curtose (momento de quarta ordem) é usada para apoiar ou opor—se aos valores próximos da média daqueles que estão mais distantes. Uma distribuição de probabilidade é dita mesocúrtica, leptocúrtica ou platicúrtica se a curtose é 0, positiva ou negativa.

Famílias

Uma distribuição é dita família exponencial a um parâmetro se sua densidade de probabilidade ou sua função massa depende de apenas uma parâmetro $\scriptstyle \theta$:

$f(y)={\begin{cases}a(\theta )b(y)\mathrm {e} ^{-c(\theta )d(y)}&{\text{ se }}\alpha <y<\beta \\0&{\text{ se não.}}\end{cases}}$

Essa família inclui muitas distribuições clássicas como distribuição normal, distribuição exponencial, distribuição Gamma, distribuição qui-quadrado, distribuição beta, distribuição de Bernoulli, distribuição de Poisson, entre outras.

Uma distribuição é dita família potência a dois parâmetros $\scriptstyle \alpha$ e $\scriptstyle \theta$ se a densidade:

$f(y)={\begin{cases}\displaystyle \alpha {\frac {y^{\alpha -1}}{\theta ^{\alpha }}}&{\text{ se }}0\leq y\leq \theta \\0&{\text{ se não.}}\end{cases}}$

Distribuição direcional

Quando uma distribuição de probabilidade multidimensional representa a direção aleatória de um fenômeno, ela é chamada de direcional. É uma distribuição de um vetor aleatório unitário de dimensão d, em que $\scriptstyle d\geq 2$, ou, de maneira equivalente, é uma distribuição de probabilidade na esfera de dimensão d. Uma distribuição direcional de dimensão d pode ser representada por um vetor (d-1-dimensional) em coordenadas polares — por exemplo, as distribuições de von Mises e de Bingham.

Momentos

Ver artigo principal: Momento (estatística)

Se existir, o n—ésimo momento de uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ é definido como $m_{n}=\int _{\Omega }\omega ^{n}\mathbb {P} (\mathrm {d} \omega )$. Essa fórmula é escrita simplesmente $\scriptstyle m_{n}=\mathbb {E} [X^{n}]$ caso a distribuição seja definida a partir de uma variável aleatória $\scriptstyle X$.

O primeiro momento ou momento de ordem 1 também é chamado de esperança da distribuição. Quando o momento é igual a 0, a distribuição é chamada de centrada. O segundo momento ou momento de ordem 2 também é chamado de variância da distribuição. Quando o momento é igual a 1, é dito que a distribuição '[e reduzida.

De uma maneira geral, a coleção de todos os momentos $\scriptstyle (m_{n},n\in \mathbb {N} )$ de uma distribuição de probabilidade não é suficiente para caracterizar cette dernière. Certas distribuições são definidas por um número finito do seu momento: a distribuição de Poisson é completamente definida por sua esperança, a distribuição normal é completamente definida por seus dois primeiros momentos. Certas distribuições não possuem momento com a distribuição de Cauchy.

Entropia

As distribuições de probabilidade permitem representar fenômenos aleatórios. A entropia de Shannon de uma distribuição de probabilidade foi introduzida em termodinâmica para quantificar a desordem molecular de um sistema. O objetivo é medir par une fonction le manque d'information de la loi de probabilité. A entropia foi definida pela primeira vez para as distribuições discretas, tendo sido estendida para as distribuições absolutamente contínuas. Para uma distribuição discreta $\scriptstyle \mathbb {P} _{1}=\sum _{i\leq n}p_{i}\delta _{x_{i}}$ e uma distribuição $\scriptstyle \mathbb {P} _{2}$ de densidade $\scriptstyle f$, a entropia H é definida respectivamente como

$H(\mathbb {P} _{1})=-\sum _{i=1}^{n}p_{i}\log _{2}(p_{i})$ e $H(\mathbb {P} _{2})=-\int _{\mathbb {R} }f(x)\ln(f(x))dx$.

• A distribuição normal é a entropia máxima para todas as distribuições possíveis que possuem a mesma média e o mesmo desvio padrão.
• A distribuição geométrica é a entropia máxima para todas as distribuições discretas que possuem a mesma média.
• A distribuição uniforme contínua é a entropia máxima para as distribuições à support borné.
• A distribuição exponencial é a entropia máxima para todas as distribuições portées par $\scriptstyle \mathbb {R} _{+}$ que possuem a mesma média. 
• As distribuições da famille puissance como a lei de Zipf são a entropia máxima parmi celles auxquelles on impose o valor do logaritmo de uma média.

O estado de entropia máxima é o estado mais desordenado, mais estável e mais provável de um sistema. Ces lois sont donc les moins prévenues de toutes les lois compatibles avec les observations ou les contraintes, et donc les seules admissibles objectivement comme distributions de probabilités a priori. Essa propriedade tem um papel importante na inferência bayeseana.

Classificação das distribuições de probabilidade na reta real

Distribuições de probabilidade em aplicações mais comuns são chamadas de distribuições discretas e distribuições absolutamente contínuas. Entretanto, existem distribuições de probabilidade que não são nem discretas nem absolutamente contínuas.

Distribuições discretas

Definição

Le support de cette loi discrète est composé des singletons {1}, {3} et {7}, les probabilités associées sont respectivement 0,2, 0,5 et 0,3.

Uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ é concentrada ou é realizada em um conjunto $\scriptstyle A\in {\mathcal {A}}$ quando $\scriptstyle \mathbb {P} (A)=1$. Uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ é dita discreta se existe um conjunto finito ou contável na qual está concentrada.

O elemento $\scriptstyle \omega \in \Omega$ é chamado de átomo de uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ quando$\scriptstyle \{\omega \}\in {\mathcal {A}}$ e $\scriptstyle \mathbb {P} (\{\omega \})\neq 0$. O conjunto de átomos de uma distribuição de probabilidade é finita ou contável. De modo geral, essa propriedade é válida para toda medida $\scriptstyle \sigma$-finita. Para uma distribuição de probabilidade real, o conjunto de átomos é exatamente o conjunto de pontos de descontinuidade de sua função de distribuição. Neste caso, a finitude do conjunto de átomos se retrouve à partir du fait que a função de distribuição é limitada.

Um critério suficiente para uma distribuição de probabilidade ser discreta é que $\scriptstyle \Omega$ seja finito ou contável.

Se $\scriptstyle \mathbb {P}$ é discreto, então ele se concentra em particular no conjunto (finito ou contável) dos seus átomos $\scriptstyle \Omega _{a}$. Para definir $\scriptstyle \mathbb {P}$ é preciso definir o conjunto dos pares: $\scriptstyle \{(\omega ,p(\omega ))\in \Omega _{a}\times ]0,1]\}$, em que $\scriptstyle p$ é a função de massa de $\scriptstyle \mathbb {P}$. Então, obtém—se

$\mathbb {P} =\sum _{\omega \in \Omega _{a}}p(\omega )\delta _{\omega }$, em que $\scriptstyle \delta _{\omega }$ é a medida de Dirac no ponto $\scriptstyle \omega \in \Omega _{a}$.

No caso em que a distribuição de probabilidade é definida a partir de uma variável aleatória, os conceitos anteriores são usados para a variável aleatória: une variable aléatoire $\scriptstyle X$ est concentrée sur un ensemble $\scriptstyle B\in {\mathcal {B}}(\mathbb {R} )$, respectivement est discrète si sa loi $\scriptstyle \mathbb {P} _{X}$ est concentrée sur $\scriptstyle B$, respectivement est discrète. Os mesmo átomos de $\scriptstyle X$ são os átomos de $\scriptstyle \mathbb {P} _{X}$.

Para uma variável aleatória discreta $\scriptstyle X$, o teorema de transferência é expresso na forma de somas ou de séries

$\mathbb {E} \left[\varphi (X)\right]=\sum _{x\in \Omega _{a}}\varphi (x)p_{X}(x)$, para toda função $\scriptstyle \varphi :\mathbb {R} \longrightarrow \mathbb {R}$,

$\mathbb {P} (X\in A)=\sum _{k\in A}\mathbb {P} (X=k)$, para todo $\scriptstyle A\in {\mathcal {B}}(\mathbb {R} )$.

Geralmente a função de distribuição de uma distribuição discreta é constante seccionalmente. Uma distribuição discreta pode ser representada por um gráfico de barras.

Exemplos

Segue uma lista de distribuições de probabilidade discretas à support finitas ou contáveis.

Medida de Dirac

A medida de Dirac é o exemplo mais simples das distribuições discretas au sens où seu support possui apenas um valor. Se uma variável aleatória é a medida de Dirac $\delta _{x}$, então $X$ é $x$ com probabilidade igual a 1. Essa lei modela um fenômeno determinista (não aleatório) pois o resultado da experiência é quase certamente igual ao valor conhecido $x$.

Distribuição uniforme discreta

A distribuição uniforme discreta modela um fenômeno aleatório cujos resultados são igualmente prováveis. É o caso do lançamento de um dado. Se o suporte $S$ da distribuição é um conjunto de $n$ elementos $\{x_{1},x_{2},\dots ,x_{n}\}$, a distribuição é definida como $\mathbb {P} (X=x_{1})=\mathbb {P} (X=x_{2})=\ldots =\mathbb {P} (X=x_{n})={\frac {1}{n}}.$

Distribuição de Bernoulli

A distribuição de Bernoulli corresponde a uma experiência com dois resultados (sucesso ou fracasso), que geralmente correspondem aos valores 1 e 0. Essa distribuição depende de um parâmetro $p\in [0,1]$para medir a probabilidade de sucesso, sendo definido por $\mathbb {P} (X=1)=1-\mathbb {P} (X=0)=p.$

Distribuição binomial

É a distribuição do número de sucessos obtidos depois de $n$ ensaios de Bernoulli independentes de parâmetros $p\in [0,1]$, ou seja, é a distribuição da soma de $n$ variáveis aleatórias independentes da distribuição de Bernoulli de mesmo parâmetro. Essa distribuição com apoio finito é definida por $\mathbb {P} (X=k)={n \choose k}p^{k}(1-p)^{n-k}$ para todo $k\in \{0,1,\dots ,n\}$.

Distribuição aritmética

É uma distribuição que concentra-se em um conjunto do tipo $\{k\cdot d,k\in \mathbb {Z} \}$, em que $d>0$.

Distribuição geométrica

É a distribuição que modela o tempo de espera do primeiro sucesso de uma de ensaios de Bernoulli independentes com probabilidade de sucesso $p\in [0,1]$. É a única distribuição discreta que possui a propriedade de falta de memória. Essa probabilidade com apoio infinito contável é definida por $\mathbb {P} (X=k)=(1-p)^{k-1}p$. para todo $k\in \mathbb {N} ^{*}$.

Distribuição de Poisson

A distribuição de Poisson descreve o comportamento do número de eventos que ocorrem em um espaço determinado de tempo. Essa distribuição com apoio infinito contável depende de um parâmetro $\lambda >0$ e é definida por $\mathbb {P} (X=k)={\frac {\lambda ^{k}}{k!}}\mathrm {e} ^{-\lambda }$ para todo $k\in \mathbb {N}$.

Distribuição hipergeométrica

A distribuição hipergeométrica modela uma retirada simultânea de $n$ bolas uma urna contendo uma proporção $pA$ de bolas vencedoras e uma proporção $(1-p)A$ de bolas perdedoras para um número total $A$ de bolas. A distribuição descreve o número de bolas extraídas. Essa distribuição com apoio finito depende de três parâmetros $n\in \mathbb {N} ^{*}$, $p\in [0,1]$ e $A\in \mathbb {N} ^{*}$e é definida por $\mathbb {P} (X=k)={\frac {{pA \choose k}{(1-p)A \choose n-k}}{A \choose n}}$ para todo $k\in \{0,1,\dots ,n\}$.

Distribuição absolutamente contínua

Definição

Uma distribuição de probabilidade real $\scriptstyle \mathbb {P}$ é chamada de absolutamente contínua ou densidade quando é absolutamente contínua par rapport à la medida de Lebesgue. Se $\scriptstyle \mathbb {P}$ é absolutamente contínua alors en vertu du teorema de Radon-Nikodym, ela possui uma densidade de probabilidade par rapport à la medida de Lebesgue. Isto é, não existe uma única (à égalité Lebesgue-presque partout près) função mensurável positiva $\scriptstyle f:\mathbb {R} \rightarrow \mathbb {R} _{+}$ de tal modo que $\scriptstyle A\in {\mathcal {B}}(\mathbb {R} )$: $\mathbb {P} (A)=\int _{A}f(x)\,\mathrm {d} x=\int _{\mathbb {R} }\mathbf {1} _{A}(x)f(x)\,\mathrm {d} x$, em que $\scriptstyle \mathbf {1} _{A}$ é a função característica de Borel $\scriptstyle A$. Essa densidade de probabilidade nem sempre tem a expressão analítica (ver os exemplos abaixo).

La courbe rouge est la densité de probabilité de la loi normale centrée réduite. Elle est appelée courbe de Gauss ou courbe en cloche.

Quando uma distribuição de probabilidade absolutamente contínua é definida a partir de uma variável aleatória $\scriptstyle X$, a variável aleatória é chamada absolutamente contínua ou densidade e a densidade da distribuição $\scriptstyle \mathbb {P} _{X}$ é igualmente chamada densidade de $\scriptstyle X$, às vezes chamada $\scriptstyle f_{X}$.

Para uma variável aleatória absolutamente contínua $\scriptstyle X$, o teorema da transferência é escrita por meio de uma integral de Lebesgue para toda função $\scriptstyle \varphi :\mathbb {R} \longrightarrow \mathbb {R}$ integral par rapport à $\scriptstyle \mathbb {P} _{X}(\mathrm {d} x)=f_{X}(x)\,\mathrm {d} x$: $\mathbb {E} \left[\varphi (X)\right]=\int _{\mathbb {R} }\varphi (x)f_{X}(x)\,\mathrm {d} x.$

A função de distribuição de uma distribuição absolutamente contínua é localmente absolutamente contínua, uma propriedade necessária e suficiente. Uma distribuição absolutamente contínua ne possède pas d'atome. Entretanto, essa propriedade que opõe-se as distribuições absolutamente contínuas às distribuições discretas não é característica das distribuições absolutamente contínuas mais des lois continues (ver a seção distribuições singulares abaixo).

As distribuições absolutamente contínuas também são chamadas de distribuições contínuas. C'est un abus de langage dû au fait que dans la plupart des applications en statistique, as distribuições contínuas são absolutamente contínuas, mas isso não é verdadeiro no caso geral.

Exemplos

Distribuição uniforme

Intuitivamente uma distribuição uniforme sobre um intervalo indica que todos os valores do intervalo tem a mesma chance de aparecer. Mais formalmente cada subintervalo $\scriptstyle [c,d]\subset [a,b]$ tem uma probabilidade igual a medida de Lebesgue de $\scriptstyle [c,d]$ (multiplicado por uma constante) d'apparaître. La loi uniforme ne dépend que de l'intervalle, son support est compact et sa densité est donnée par :

$f(x)={\frac {1}{b-a}}$ para $x\in [a,b]$.

$f(x)=0$ se não.

Distribuição exponencial

A distribuição exponencial é comumente usada para modelar o tempo de vida de um fenômeno pois é a única distribuição absolutamente contínua com propriedade de falta de memória. En ce sens elle est l'analogue continu de la loi géométrique. Essa distribuição com apoio semi-infinito depende de um parâmetro (às vezes chamado de intensidade), em que a densidade é definida como $f(x)=\lambda \mathrm {e} ^{-\lambda x}$ para todo $\scriptstyle x\geq 0$.

Distribuição normal

Uma distribuição normal ou distribuição gaussinana é uma distribuição central na teoria da probabilidade. Ela descreve o comportamento de séries de experiências aleatórias quando o número de tentativas é muito grande. É a distribuição limite do teorema central do limite. Ela é igualmente a única distribuição estável de parâmetro 2. A distribuição normal é caracterizada por sua média (que também é sua mediana) e seu desvio-padrão, son support est la droite réelle. Sua densidade é simétrica e sua forma é comumente chamada de curva de Gauss ou curva em sino: $f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\mathrm {e} ^{-{\frac {(x-m)^{2}}{2\sigma ^{2}}}}$.

Distribuição de Cauchy

A distribuição de Cauchy é a distribuição estável de parâmetro 1, ce qui lui donne de bonnes propriétés. Entretanto, é um exemplo típico de distribuição que não admite momentos, em particular nem média nem variância. Son support est la droite réelle e sua densidade é simétrica e definida por $f(x)={\frac {1}{\pi }}{\frac {1}{1+x^{2}}}$. A distribuição da posição de um movimento browniano plan au moment où celui-ci atteint la droite $\scriptstyle y={\frac {1}{2}}$ é uma distribuição de Cauchy.

Distribuição de Tukey-Lambda

Uma distribuição de Tukey-Lamba é uma distribuição absolutamente contínua. Logo possui uma densidade de probabilidade, mas não possui uma expressão analítica. Essa distribuição depende de um parâmetro, son support est soit un intervalle borné centré à l'origine, soit la droite réelle (en fonction du paramètre). A distribuição de Tukey-Lambda é definida a partir da função quantil: $Q(p)={p^{\lambda }-(1-p)^{\lambda } \over \lambda }$.

Lois singulières

Définition

Une loi de probabilité $\scriptstyle \mathbb {P}$ est dite continue ou diffuse lorsqu'elle ne possède pas d'atome.

En particulier, les lois absolument continues sont continues, la réciproque n'est cependant pas vraie. La fonction de répartition d'une loi de probabilité réelle continue est continue, c'est une propriété nécessaire et suffisante.

Une loi de probabilité $\scriptstyle \mathbb {P}$ est dite singulière lorsqu'elle est continue mais pas absolument continue. C'est-à-dire qu'une loi singulière ne possède ni atome, ni densité.

Ces notions se disent également pour les lois de probabilité définies à partir de variables aléatoires : une variable aléatoire $\scriptstyle X$ est continue (ou diffuse), respectivement singulière, lorsque sa loi de probabilité associée $\scriptstyle \mathbb {P} _{X}$ est continue (ou diffuse), respectivement singulière.

Exemple

Loi de Cantor

Fonction de répartition de la loi de Cantor.

C'est une loi singulière. Elle est définie à partir de l'ensemble de Cantor : $\scriptstyle \left\{\sum _{n=1}^{\infty }{\frac {x_{n}}{3^{n}}}\ |\,x_{n}\in \{0,2\}\right\}$. Lorsque $\scriptstyle X_{n}$ sont des variables indépendantes et identiquement distribuées de loi uniforme discrète sur $\scriptstyle \{0,2\}$, alors

$X=\sum _{n=1}^{\infty }{\frac {X_{n}}{3^{n}}}$

est une variable aléatoire de loi de Cantor. Cette loi de probabilité s'écrit sous la forme $\scriptstyle \mathbb {P} _{X}=({\frac {1}{2}}\delta _{0}+{\frac {1}{2}}\delta _{2})^{\otimes \mathbb {N} }$, c'est la loi uniforme sur l'ensemble de Cantor. Sa fonction de répartition est l'escalier de Cantor, elle est dérivable presque partout et de dérivée nulle presque partout.

Dans les applications, il est rare que les lois continues contiennent une partie singulière. L'ensemble de Cantor apparaît toutefois dans certains exemples bien connus : l'ensemble des zéros du mouvement brownien est un ensemble de type Cantor.

Autres cas

Il existe des lois de probabilité qui ne sont ni discrètes, ni absolument continues, ni singulières, elles sont parfois appelées lois mixtes · .

D'un point de vue plus général, toute loi de probabilité $\scriptstyle \mathbb {P}$ peut se décomposer · en une combinaison linéaire d'une loi continue $\scriptstyle \mathbb {P} _{\text{c}}$ et d'une loi discrète $\scriptstyle \mathbb {P} _{\text{d}}$. De plus le théorème de décomposition de Lebesgue appliqué à $\scriptstyle \mathbb {P} _{\text{c}}$ indique que cette loi continue se décompose en une combinaison linéaire de deux lois continues, l'une $\scriptstyle \mathbb {P} _{\text{ac}}$ est absolument continue par rapport à la mesure de Lebesgue et l'autre $\scriptstyle \mathbb {P} _{\text{s}}$ est singulière, étrangère à la mesure de Lebesgue. La décomposition s'écrit donc :

$\mathbb {P} =\alpha \mathbb {P} _{\text{d}}+(1-\alpha )\mathbb {P} _{\text{c}}=\alpha \mathbb {P} _{\text{d}}+\beta \mathbb {P} _{\text{ac}}+\gamma \mathbb {P} _{\text{s}}$

avec $\alpha ,\beta ,\gamma \in [0,1]$ et $\alpha +\beta +\gamma =1$. La présence de $\scriptstyle (\alpha ,\beta ,\gamma )$ assure que $\scriptstyle \mathbb {P} (\Omega )=1$.

Exemple de fonction de répartition d'une loi mixte.

La loi de probabilité réelle suivante est un exemple de loi mixte obtenue en mélangeant une loi discrète, définie par ses atomes $\scriptstyle \{x_{k},k\in \mathbb {N} \}$ et sa fonction de masse $\scriptstyle p$, avec une loi absolument continue de densité $\scriptstyle f$ :

$\mathbb {P} (\mathrm {d} x)=\alpha f(x)\,\mathrm {d} x+(1-\alpha )\sum _{k\in \mathbb {N} }p(x_{k})\delta _{x_{k}}(\mathrm {d} x)$

où $\scriptstyle \alpha \in ]0,1[$. Sa fonction de répartition est une fonction continue par morceaux, mais pas constante par morceaux ce qui est le cas des fonctions de répartition des lois discrètes.

Intuitivement, cela correspond à un phénomène aléatoire dont la loi est absolument continue. Cependant l'appareil de mesure ne peut mesurer les données qu'à partir d'un certain seuil c. Toutes les mesures non détectées par l'appareil seront assignées à 0, ainsi la loi est nulle sur toute partie « plus petite » que c alors qu'un saut apparaît au singleton c. Les mesures suivent la loi absolument continue pour les valeurs plus grandes que c. Dans cet exemple la fonction de répartition est discontinue en c.

Caractérisations d'une loi de probabilité

Il existe plusieurs fonctions à variables réelles ou complexes qui déterminent de manière unique les lois de probabilités. Les propriétés de certaines de ces fonctions permettent de déduire des propriétés pour les lois comme le calcul des moments ou une expression de la convergence en loi.

À l'aide de la fonction de répartition

Fonction de répartition de la loi normale centrée réduite.

Predefinição:Article détaillé D'après le lemme de classe monotone, les ensembles $\scriptstyle ]-\infty ,x]$, appelés pavés ou rectangles, engendrent la tribu borélienne réelle $\scriptstyle {\mathcal {B}}(\mathbb {R} )$, il suffit alors de définir une loi de probabilité sur les pavés. On suppose que la loi de probabilité est réelle, c'est-à-dire $\scriptstyle (\Omega ,{\mathcal {A}})=(\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))$.

La fonction de répartition d'une loi de probabilité $\scriptstyle \mathbb {P}$ réelle, notée par $\scriptstyle F$, est la fonction définie par, pour tout $\scriptstyle x\in \mathbb {R}$ :

$F(x)=\mathbb {P} {\big (}]-\infty ,x]{\big )}.$

Une loi de probabilité est caractérisée par sa fonction de répartition, c'est-à-dire que deux lois de probabilités sont égales si et seulement si leurs fonctions de répartitions sont égales.

Plus généralement, toute fonction $\scriptstyle F$ croissante, continue à droite et vérifiant : $\scriptstyle \lim _{x\to -\infty }F(x)=0$ et $\scriptstyle \lim _{x\to \infty }F(x)=1$ est la fonction de répartition d'une unique loi de probabilité sur $\scriptstyle \mathbb {R}$. La loi de probabilité définie à partir d'une fonction de répartition est appelée mesure de Lebesgue-Stieltjes.

Un des avantages de la fonction est qu'elle est bien définie pour toute loi de probabilité. Cependant elle n'a pas toujours d'expression explicite, un exemple étant la fonction de répartition de la loi normale. La fonction de répartition permet parfois des calculs de lois aisés (loi du maximum ou du minimum d'un échantillon, e.g.) et fournit un critère commode de convergence des lois de probabilités via le théorème porte-manteau.

À l'aide de la fonction caractéristique

Fonction caractéristique de la loi uniforme continue sur [-1,1]. Puisque la loi est symétrique, la fonction caractéristique est réelle.

Predefinição:Article détaillé On appelle fonction caractéristique d'une loi de probabilité $\scriptstyle \mathbb {P}$, et l'on note $\scriptstyle \Phi$, la « symétrie » de la transformée de Fourier de $\scriptstyle \mathbb {P}$. Pour tout $\scriptstyle t\in \mathbb {R}$ :

$\Phi (t)={\mathcal {F}}(\mathbb {P} )(-t)=\int _{\Omega }\mathrm {e} ^{\mathrm {i} t\omega }\,\mathbb {P} (\mathrm {d} \omega ).$

Suivant la définition de la transformée de Fourier, la fonction caractéristique est sa symétrique ou non. Comme son nom l'indique, la fonction caractéristique détermine la loi de manière unique, c'est-à-dire que deux lois de probabilité sont égales si et seulement si leurs fonctions caractéristiques sont égales.

Un des avantages de la fonction caractéristique est qu'elle existe pour toute loi de probabilité · . De plus, en utilisant la formule d'inversion de la transformée de Fourier, la loi de probabilité s'obtient à partir de la fonction caractéristique. La représentation des lois par la fonction caractéristique permet également de caractériser la convergence des lois de probabilités via le théorème porte-manteau.

Dans le cas où la loi de probabilité est définie à partir d'une variable aléatoire $\scriptstyle X$, d'après le théorème de transfert, pour tout $\scriptstyle t\in \mathbb {R}$ :

$\Phi _{X}(t)=\int _{\mathbb {R} }\mathrm {e} ^{\mathrm {i} tx}\,\mathbb {P} _{X}(\mathrm {d} x)=\int _{\Omega }\mathrm {e} ^{\mathrm {i} tX(\omega )}\,\mathbb {P} (\mathrm {d} \omega )=\mathbb {E} \left[\mathrm {e} ^{\mathrm {i} tX}\right].$

À l'aide de la fonction génératrice des moments

Fonction génératrice des moments de la loi uniforme continue sur [-1,1].

Predefinição:Article détaillé La fonction génératrice des moments d'une loi de probabilité $\scriptstyle \mathbb {P}$, notée $\scriptstyle M$, est la « symétrie » de la transformée de Laplace de $\scriptstyle \mathbb {P}$ · . Lorsque la fonction $\scriptstyle \omega \mapsto e^{t\omega }$ est intégrable par rapport à la mesure $\scriptstyle \mathbb {P}$, pour tout $\scriptstyle t\in \mathbb {R}$ :

$M(t)={\mathcal {L}}(\mathbb {P} )(-t)=\int _{\Omega }\mathrm {e} ^{t\omega }\,\mathbb {P} (\mathrm {d} \omega ).$

La fonction génératrice des moments détermine la loi de probabilité de manière unique si cette fonction existe sur un intervalle contenant l'origine.

Un des avantages de cette fonction génératrice des moments est qu'elle permet de retrouver les moments de la loi de probabilité par les dérivées. Pour tout $\scriptstyle k\in \mathbb {N}$, la $\scriptstyle k$-ième dérivée de la fonction génératrice des moments en 0 est le moment d'ordre $\scriptstyle k$ de la loi de probabilité :

$M^{(k)}(0)=\int _{\Omega }\omega ^{k}\mathbb {P} (\mathrm {d} \omega )$.

La représentation des lois par la fonction génératrice des moments permet également de caractériser la convergence des lois de probabilités via le théorème porte-manteau.

Dans le cas où la loi de probabilité est définie à partir d'une variable aléatoire $\scriptstyle X$, d'après le théorème de transfert, pour tout $\scriptstyle t\in \mathbb {R}$ :

$M_{X}(t)=\int _{\mathbb {R} }\mathrm {e} ^{tx}\,\mathbb {P} _{X}(\mathrm {d} x)=\int _{\Omega }\mathrm {e} ^{tX(\omega )}\,\mathbb {P} (\mathrm {d} \omega )=\mathbb {E} \left[\mathrm {e} ^{tX}\right]$.

De plus, pour des lois définies à partir de variables aléatoires, cette fonction permet aisément de montrer l'indépendance des variables.

Predefinição:Article détaillé Il existe un cas particulier pour les lois discrètes. La fonction génératrice des probabilités d'une loi de probabilité discrète $\scriptstyle \mathbb {P} =\sum _{k}p_{k}\delta _{k}$ est définie comme l'espérance de la série génératrice : $\scriptstyle g(t)=\sum _{k}t^{k}p_{k}$, sous réserve d’existence de cette série. Cette fonction génératrice détermine la loi de probabilité de manière unique.

Autres caractérisations

Exemple de quantiles.

Predefinição:Article détaillé La fonction quantile d'une loi de probabilité réelle $\scriptstyle \mathbb {P}$, notée $\scriptstyle Q$, est la fonction qui donne les quantiles de la loi. Elle est définie par, pour tout $\scriptstyle p\in ]0,1[$ :

$Q(p)=\inf\{u\in \mathbb {R} \ |\ F(u)\geq p\}$

où $\scriptstyle F$ est la fonction de répartition de $\scriptstyle \mathbb {P}$.

Certaines lois de probabilité sont plus faciles à définir, via leur fonction quantile. Intuitivement, $\scriptstyle Q(p)$ est la valeur telle qu'une proportion $\scriptstyle x$ des valeurs possibles de la loi lui soit inférieure. $\scriptstyle Q({\frac {1}{4}})$, $\scriptstyle Q({\frac {1}{2}})$, et $\scriptstyle Q({\frac {3}{4}})$ sont respectivement le Predefinição:1er quartile, la médiane et le Predefinição:3e quartile de la loi.

Si $\scriptstyle F$ est bicontinue alors $\scriptstyle Q$ est la fonction réciproque de la fonction de répartition : $\scriptstyle Q=F^{-1}$, c'est pour cela que dans le cas général on appelle aussi la fonction quantile réciproque généralisée de $\scriptstyle F$ ou fonction inverse continue à droite de $\scriptstyle F$.

Cette fonction quantile détermine la loi associée $\scriptstyle \mathbb {P}$ au sens où, si $\scriptstyle U$ est une variable aléatoire de loi uniforme continue sur [0,1], alors $\scriptstyle Q(U)$ est une variable aléatoire de loi $\scriptstyle \mathbb {P}$ initiale. Cette représentation est particulièrement utile pour simuler des lois de probabilité puisqu'il suffit alors de simuler une loi uniforme continue et d'y appliquer la fonction quantile (voir la section ci-dessous sur la simulation des lois de probabilités).

Certaines lois n'ont pas de fonction de répartition explicite mais sont définies à partir de leur fonction quantile, c'est le cas de la loi de Tukey-Lambda.

Utilisations

La répartition statistique d'une variable au sein d'une population est souvent voisine des modèles mathématiques des lois de probabilités. Il est souvent intéressant, pour des raisons théoriques et pratiques, d'étudier le modèle probabiliste, dit théorique. L'étude commence alors par une sélection au hasard de plusieurs valeurs ou individus. Si la méthode utilisée est parfaite, c'est-à-dire que ces valeurs observées sont issues d'une sélection équiprobable, alors elles sont des variables aléatoires et l'étude du phénomène revient à étudier la loi de probabilité.

Simulation d'une loi de probabilité

Simulation de la loi uniforme continue sur le carré unitaire. On remarque ici l'imperfection des Predefinição:Unité pseudo-aléatoires par la présence de zones moins denses.

Predefinição:Article détaillé Afin d'étudier les lois de probabilité, il est important de pouvoir les simuler, ceci est dû notamment à l’utilisation de l'informatique dans les sciences. Comme indiqué ci-dessus, les lois de probabilité sont caractérisées par la fonction quantile via une variable aléatoire de loi uniforme continue. Cette méthode générale comprend deux étapes : la génération de valeurs dites pseudo-aléatoires de loi uniforme et l'inversion de la fonction de répartition de la loi étudiée. Cette deuxième étape n'est pas évidente à réaliser pour toutes les lois, d'autres méthodes sont alors utilisées.

Predefinição:Citation bloc

Simulation de la loi uniforme

Pour obtenir des valeurs suivant la loi uniforme continue, l'ordinateur simule des valeurs de la loi uniforme discrète. Plusieurs méthodes ont été utilisées : l'utilisation de tables de données qui pouvaient en contenir plus d'un million est de moins en moins utilisée ; l'utilisation de processus physique comme la création d'un bruit électronique est assez coûteuse pour la récupération des données ; l'utilisation d'algorithmes arithmétiques est la méthode la plus simple. Ces algorithmes étant déterministes (non aléatoires), les valeurs obtenues sont appelées pseudo-aléatoires. De nombreux algorithmes ont été créés pour améliorer l'indépendance entre les valeurs et leur répartition dans l'intervalle $\scriptstyle [0,1]$.

Simulation des autres lois

Lorsque la fonction de répartition est inversible, on utilise la caractérisation par la fonction quantile. Quelques exemples illustrent des cas où cette fonction n'est pas inversible : la méthode de Box-Muller permet de simuler la loi normale, la méthode de rejet de von Neumann est fondé sur un test statistique et est applicable pour plusieurs lois, d'autres méthodes spécifiques aux lois existent.

Exemple

Un exemple renommé d'utilisation d'une simulation de loi de probabilité est la méthode de Monte-Carlo, par exemple pour approcher la valeur de π. La méthode consiste à simuler un grand nombre de valeurs suivant une loi uniforme continue sur $\scriptstyle [0,1]$ et de compter la proportion des couples $\scriptstyle (x,y)$ d'entre eux qui vérifient $\scriptstyle x^{2}+y^{2}\leq 1$. Cette proportion se rapproche de $\scriptstyle {\frac {\pi }{4}}$ lorsque le nombre de points tend vers l'infini.

Approximation d'une loi de probabilité

Illustration du théorème central limite. Les données empiriques sont les valeurs possibles de la somme de $\scriptstyle n$ dés ($\scriptstyle n\in \{1,2,3,4,5\}$) à six faces lancés au hasard. Lorsque $\scriptstyle n$ augmente, les histogrammes convergent vers la courbe de Gauss qui est la densité de la loi normale.

Plusieurs approximations d'une loi de probabilité existent en utilisant les différentes caractérisations détaillées ci-dessus. C'est généralement les techniques utilisées dans les cas pratiques. La première étape est la récolte des données, ce qui permet de construire les objets empiriques comme la fonction de répartition empirique. Ces derniers sont parfois appelés, par abus de langage, des lois de probabilité mais ce sont en fait des lois empiriques appelées distributions statistiques. Des théorèmes limites ou des tests statistiques permettent finalement d'identifier la meilleure loi de probabilité qui modélise le phénomène aléatoire initial.

Par la fonction de répartition

Le test statistique de Kolmogorov-Smirnov, basé sur le théorème porte-manteau, permet d'identifier la fonction de répartition empirique calculée à partir des données à une fonction de répartition d'une loi de probabilité, en fonction d'un taux de rejet. L'avantage de la convergence des fonctions de répartition est que ces fonctions existent pour toutes lois de probabilités. Cette convergence permet en particulier d'approcher une loi absolument continue par une suite de lois discrètes.

Convergence des autres fonctions caractéristiques

Différents théorèmes de convergence de variables aléatoires permettent de construire une suite de lois de probabilité qui converge vers une loi donnée, ou inversement de construire une loi comme limite de lois de probabilité. Le théorème central limite concerne la loi normale pour loi limite. Le théorème de continuité de Paul Lévy concerne la convergence des fonctions caractéristiques.

Exemple de droite de Henry dans un diagramme Quantile-Quantile qui permet de comparer visuellement les quantiles empiriques aux quantiles théoriques. Ici la loi normale n'est pas adéquate.

Régression quantile

La régression quantile permet d'approcher les quantiles de la loi par les quantiles empiriques, c'est-à-dire calculés à partir d'éventuelles données. On peut utiliser un test statistique pour comparer les quantiles empiriques (observés) avec les quantiles de la loi qui est supposée modéliser le phénomène.

Cette approche est particulièrement utile pour étudier certaines lois qui ne sont pas connues explicitement par leur densité ou leur fonction de répartition mais par leurs quantiles, c'est le cas de la loi de Tukey-Lambda.

Tests statistiques

Plusieurs tests statistiques existent pour comparer deux lois. Plus précisément, les tests d'adéquation permettent de comparer une loi empirique (c'est-à-dire calculée à partir des données issues d'échantillons) à une loi de probabilité dite a priori qui est censée modéliser le phénomène étudié. Les deux principaux tests sont : le test de Kolmogorov-Smirnov mentionné ci-dessus qui compare les fonctions de répartition et le test d'adéquation du χ² qui compare les effectifs observés avec une loi du χ². Parmi ces tests, ceux qui concernent la loi normale sont dits tests de normalité.

Les tests d’homogénéité permettent de comparer deux lois empiriques pour savoir si elles sont issues du même phénomène ou, de manière équivalente, si elles peuvent être modélisées par la même loi de probabilité a priori. Ces tests comparent certaines propriétés des lois empiriques à la propriété de la loi a priori. Ils sont utiles dans la pratique puisqu'ils permettent de comparer non pas des lois entières mais des valeurs issues des lois : le test de Fisher estime le rapport des variances empiriques via la loi de Fisher, le test de Student estime la moyenne empirique via la loi de Student, etc.

Exemples de modélisation

Les lois de probabilité sont utilisées pour représenter les phénomènes observés. Une loi de probabilité, dite a priori, est supposée modéliser les données récupérées, des tests statistiques sont alors réalisés pour affirmer ou infirmer la concordance de la loi de probabilité avec les données. Dans bien des domaines, les méthodes ont évolué et de meilleures lois de probabilité ont été créées afin de mieux correspondre au problème posé. Voici une liste d'exemples concrets qui proposent des modélisations :

• en économie : la bourse est une institution qui permet d'échanger des biens ou des titres. Afin de mieux estimer le prix futur d'un bien ou d'un titre, une étude de l'évolution historique de son prix est réalisée, notamment par la modélisation des variations des cours des prix. Ces variations ont d'abord été modélisées par une loi normale (Bachelier, 1900), puis une amélioration a été faite avec les lois stables de Pareto (Mandelbrot, 1963). Depuis, de nouveaux modèles sont toujours recherchés pour améliorer la perception des risques ;
• aux jeux de hasard : pour jouer au loto français, il faut choisir six numéros parmi les quarante-neuf possibles. Si les joueurs choisissent leurs numéros au hasard, c'est-à-dire avec une loi uniforme discrète, alors le nombre de gagnants suit une loi de Poisson. Grâce à cette considération, une étude peut être réalisée puisque le nombre de gagnants est une donnée connue. Il apparaît que le choix n'est pas uniforme mais que les petits numéros ont été plus choisis ;
• en maintenance : une bonne compréhension de la dégradation permet d'améliorer la performance de la maintenance. Plusieurs lois a priori ont été utilisées pour modéliser l'évolution de la fissure des chaussées : la loi exponentielle, la loi de Weibull, la loi log-normale, la loi log-logistique, etc. Pour une utilisation de la méthode du maximum de vraisemblance, la loi log-logistique fait partie des lois les plus adaptées ;
• en médecine : pour tester l'efficacité des médicaments, un essai clinique est réalisé auprès d'un échantillon d'utilisateurs. Cette méthode fait partie de la théorie de la décision. Une des méthodes est de sélectionner un malade pour réaliser un test avec deux issues (succès ou échec), c'est-à-dire de modéliser par une loi de Bernoulli, puis de recommencer le plus de fois possibles ; c'est la méthode des urnes de Bernoulli. Une meilleure méthode est d'utiliser la loi hypergéométrique, ce choix permet de ne considérer qu'une population d'individus de taille fixée préalablement ;
• en météorologie : en hydrologie, la pluviométrie est l'étude de la quantité d'eau issue de la pluie tombée en un point du sol pendant une durée de temps fixée. Le choix de la loi a priori ne fait pas consensus au sein de la communauté scientifique internationale. Certains auteurs préconisent l'utilisation de la loi log-normale qui s'ajuste bien aux petites valeurs. D'autres proposent la loi Gamma qui s'ajuste bien aux valeurs expérimentales. L'utilisation de la loi de Pareto a son intérêt pour représenter les valeurs moyennes.

Referências

Articles

Voir aussi

Bibliographie

• [S.l.: s.n.] ISBN 978-2-86883-931-2  .Predefinição:Plume
• [S.l.: s.n.] ISBN 2-8041-4794-0  .Predefinição:Plume
• [S.l.: s.n.]  .Predefinição:Plume
• [S.l.: s.n.] ISBN 978-2-8178-0162-9  .Predefinição:Plume
• [S.l.: s.n.] ISBN 978-2-88074-794-7  .Predefinição:Plume
• [S.l.: s.n.] ISBN 2-909963-08-X  .Predefinição:Plume
• [S.l.: s.n.]  .Predefinição:Plume
• [S.l.: s.n.] ISBN 978-2-287-99307-7  .Predefinição:Plume
• [S.l.: s.n.] ISBN 1-86094-555-4  .Predefinição:Plume
• [S.l.: s.n.] ISBN 3-540-52013-9  .Predefinição:Plume
• [S.l.: s.n.] ISBN 978-2844728289  .Predefinição:Plume
• [S.l.: s.n.] ISBN 2-88074-286-2  .Predefinição:Plume
• [S.l.: s.n.] ISBN 0-387-20270-6  .Predefinição:Plume
• Predefinição:Saporta1.Predefinição:Plume
• [S.l.: s.n.] ISBN 978-0387945491  .Predefinição:Plume
• (em inglês) [S.l.: s.n.]  .Predefinição:Plume